论分色与加网的相关性

成刚虎， 李云香， 吴　娇

(西安理工大学 印刷包装与数字媒体学院，陕西 西安 710048)



论分色与加网的相关性

成刚虎， 李云香， 吴娇

(西安理工大学 印刷包装与数字媒体学院，陕西 西安 710048)

半色调原理是现代彩色印刷的物理基础，分色和加网是彩色印刷印前处理过程中的核心内容。作为两个不可或缺的工艺过程，长期以来分色和加网一直被业内当作(或假设为)两道独立的操过工序进行作业。由此引入的系统误差也一直被人们忽视。基于色光加色法，针对分色与加网的关系和影响，本文进行了理论考查和仿真分析。研究结果表明：加网方法随分色过程而确定，分色模型及结果因加网方法(或假设)而改变。由此得出结论：分色和加网在理论上是相关的，不具有相互独立性。

分色； 加网； 相关性； 系统误差

半色调印刷是包括数字印刷在内的现代彩色印刷呈色的重要物理基础。要实现半色调彩色印刷，制版过程中总是少不了分色和加网两道核心印前处理工序[1-2]。无论模拟分色(包括照相分色和模数电子分色)还是数字分色，也不管分色和加网同时进行还是分开进行，逻辑上人们总是认为先分色，后加网[2-3]，而且长此以往自觉不自觉地将二者看作两道独立的印前操作工序。

在长期的印刷质量研究分析中，一般都是根据研究需要设计印刷测试版，然后依次进行分色、加网和印刷，接着进行效果测试分析，计算相对于原稿(测试版)的呈色色差，并不断研究分色新方法、加网新模型，希望减小、控制呈色误差。但是其结果总难以如愿，始终没能找到理想的方法和模型[4-7]。

其实，影响印刷流程误差积累的因素和参数很多，除了不可控的随机误差之外，系统误差的影响尤其值得关注。理论分析和仿真实验研究均表明：在半色调印刷印前处理过程中，分色和加网不具有相对独立性。由独立性假设引发的系统误差不容小觑。笔者以为，这也是迄今为止国内印刷业界的最大误区之一。

从某种意义上讲，这种现状一定程度上制约着国内印刷业的品质提升。为此本文开展如下研究。

首先，以色光加色法为依据，分析色料呈色机理，说明色空间的转换原理，揭示分色的逻辑流程与加网的本质内容；接着，依据理论研讨和仿真模拟，通过呈色分析，阐明呈色效果的不确定性及其与加网的相关性；然后，通过分析独立分色的困难和条件，总结现行操作过程的实际内涵，以及分色效果与加网参数的关系(仿真曲线)，说明分色结果对加网的依赖性；最后，总结全文做出判断，简要阐明分色与加网的相互制约关系。

1　分色、加网的逻辑过程

彩色图像依靠分色过程完成RGB(或XYZ)到CMY色彩空间的转换[4-7]，通过加网实现连续图像的半色调转化，即二值化[3]，以便制版输出。

1.1分色的逻辑过程

分色过程就是一个色空间转换过程，一般以色度匹配平衡为基础[1-2]，即针对原稿上的每一个像素，逐一进行色度匹配计算，完成色空间转换。具体过程如下。

1.1.1从色度平衡到色元面积率

印品上色彩感觉的形成是通过(色料叠加所产生的)色元的色光加色合成实现的。分色的第一步就是依据色光加色法，将画面上所有像素的色度(通过色度平衡原理)转换成色元面积率的过程。

一般而言，三色印刷时，每个像素点(即呈色单元)在微观结构上最多由8个色元构成，即：白、黄、品、青、红、绿、蓝、黑。按照Grassman色光混合定律[1-2]，色料呈色的物理(过程)模型可简单表示为式(1)的形式(色度匹配平衡方程)，也就是享誉业界的纽介堡方程(Neugebauer equation)[1-2]。即：

(1)

其中，X、Y、Z为匹配色(或生成色)的三刺激值；Xi、Yi、Zi分别代表各色元的三刺激值；fi(i=1,2,3,4,5,6,7,8)依次代表8个色元(白、黄、品、青、红、绿、蓝、黑)的面积率。而且，根据色元面积率的基本概念，8个色元面积率之间满足式(2)[8]：

f1+f2+f3+f4+f5+f6+f7+f8=1

(2)

1.1.2从色元面积率到色版面积率

分色的终极目的就是要取得(版面上所有像素的)色版面积率。通过公式(1)和(2)可取得色元面积率，下面，需要据此来确定色版面积率。

根据色元的形成过程可知，色元面积率与色版面积率之间的关系可以用式(3)来表征[8，16]。

(3)

式中，y、m、c分别表示黄版、品红版、青版的色版面积率；fi(i=1,2,3,4,5,6,7,8)含义同前。

依据(3)式即可求得色版面积率m、y。

1.1.3黑版计算[2]

为解决三色印刷中实际的三原色油墨主密度偏小、副密度偏大，特别是暗调灰色不够的问题，实际印刷中一般还要增加黑版。

黑版值是三原色CMY的函数，黑版由其与CMY的关系产生，黑版量(即黑版面积率k)由CMY量(c、m、y)计算而来。一般采用底色去除(UCR)、非彩色结构(GCR)以及底色增益(UCA)等工艺方法来生成黑版(具体过程这里不赘述)。

综上，分色的逻辑过程可以描述为：首先，测定特定(给定纸张、油墨、印刷设备等)条件下各色元色度值Xi、Yi、Zi；其次，依据色光加色法，即式(1)和(2)，取得色元面积率fi(i=1,2,3,4,5,6,7,8)；接着，通过方程(3)计算出色版面积率y、m、c；最后，选择黑版生成工艺，计算出黑版面积率k。

1.2加网的逻辑过程

加网是半色调印刷的根本所在。连续调图像必须通过加网才能转变成网目调图像完成印刷。基于色度平衡的分色完成以后，形成连续调单色图像；通过加网，将分色后的连续调单色图像转变为半色调的单色图像。同时，通过合理加网参数的选择，可以消除半色调印刷中的典型性呈色倾向，如玫瑰斑、龟纹等，控制视觉误差[2]。

数字加网在逻辑上分为两步，即选择加网模版和加网计算。

加网操作的内容，首先就是确定各种加网参数，包括：加网线数、加网角度、加网形式和网点形状等[2]。加网模板在设计上包含了各种加网参数。

加网计算，就是对画面上所有的网目调网点逐一进行分配计算，一般由计算机自动完成。其本质就是对网点的微观形态做出几何上的安排和设计。图1所示为三种不同加网模型的0°模板。从中可以看出，在网目调单元内，包含着一定量的机器点(其多少受制于加网线数)，不同的模板具有不同的机器点曝光顺序。网点面积率决定了曝光点多少，而曝光的具体位置则由模板确定。

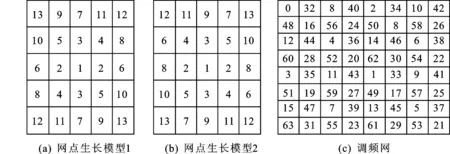
图1　不同的网点生长模型Fig.1　The different dot growth modles

2　加网的分色相关性

加网是印前处理的关键步骤，是获得良好印品的核心工序，通过加网完成灰度图像的二值化处理。但同时加网处理也确定了半色调图像中不同色版对应网点的相互关系。因此，加网具有呈色效果的决定性。

2.1理论呈色效果的加网依赖性

半色调印刷中，彩色图像由无穷个像素组成。显然，只有每一个像素的色度都唯一确定，方可使图像色调完全确定。然而，完成了分色，未经加网，尚不能对印刷输出的理论色调(除少数像素外)做出客观正确的预测。

2.1.1理论色度随加网而确定

加网本质表明：单一网点的理论色度、从而整幅画面的理论色调由加网唯一确定。这里仍借用(1)式和(3)式予以说明。(1)式表明，只有色元面积率完全确定之后，才可以对理论呈色效果做出正确预判。然而由(3)式可知：(分色后)确定了色版面积率y、m、c，色元面积率fi却没有确定解[8]。因为此时，(3)式在数学上是一个不定方程组。如果考虑黑版的影响，只是色元数多一些而已，其分析逻辑亦然。这就是说，即使分色能够顺利而无误差地完成，取得了色版面积率y、m、c之后，其实并不能准确推知色元面积率fi，从而也不能(利用方程(1))精确预测理论色度；或者说，仅凭分色结果并不能预知理论呈色结果。分色完成以后，理论呈色效果还不具有确定性。加网处理时，在对各像素进行二值化处理过程中，网点的形态及其生长过程便固定下来，不同色版微观印刷区域(网点)的相对位置关系也随之确定。

这里以网点生长模型[2]为例对此加以简单分析。图2和图3分别是两种不同的加网模板及其不同加网角度的网点生长模型。

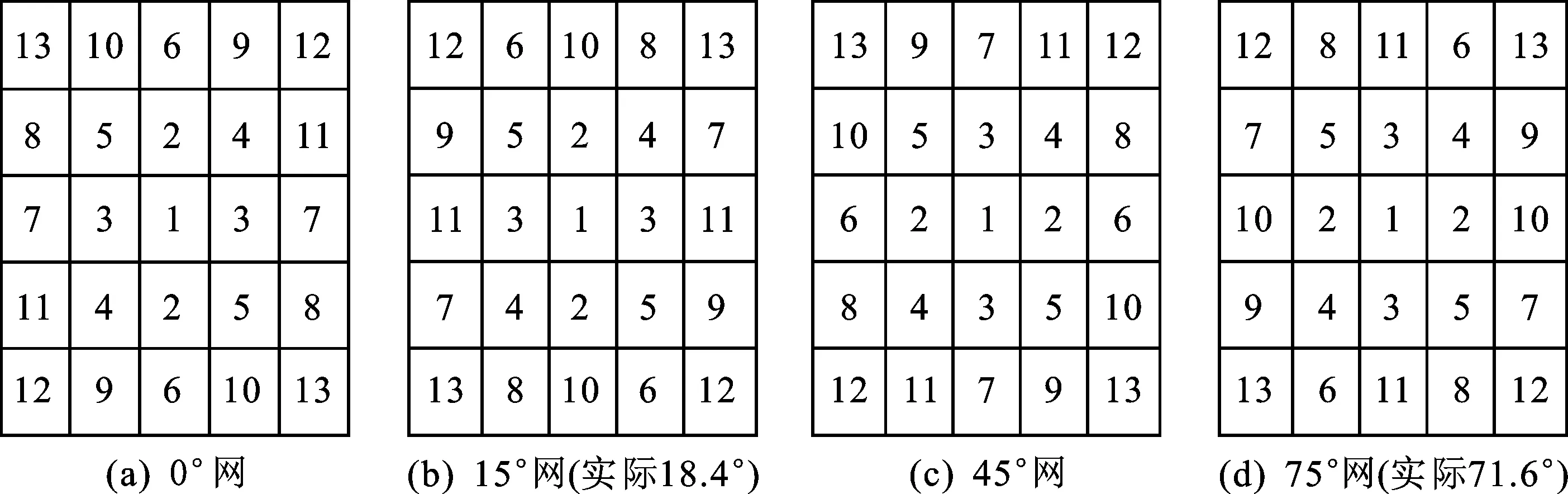
图2　网点生长模型1及其加网角度Fig.2　The dot growth modle 1 with different screen angles

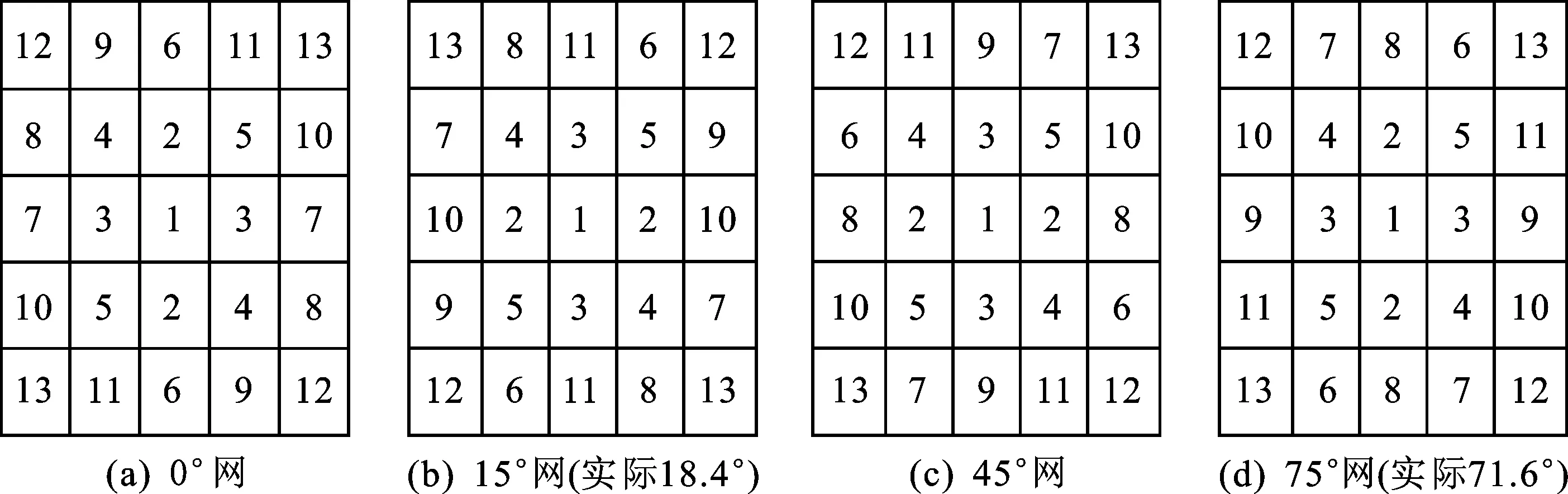
图3　网点生长模型2及其加网角度Fig.3　The dot growth modle 2 with different screen angles

由图1～3可以看出，无论哪种加网模板，都具有确定的色版间对应关系。由此可知，确定了加网方法，就可以确定不同色版面积率下的网点并列、重叠关系，各色元面积率fi(i=1,2,3,4,5,6,7,8)便随之确定，即方程(3)的反求有了确定解。这样，通过方程(1)，就可以对呈色效果做出预判。

综上，理论印刷呈色效果非加网不能确定。虽然色元面积率与加网的关系比较复杂，随着色域的变化以及加网参数(加网线数、加网角度、网点形态等)的变化而变化，不可能用一个简单的关系模型表达或替代，但是分析表明：只有确定了加网方法，给定色版面积率条件下的色元面积率才具有唯一性。从而每个色块的色度以及整个版面的色调也才唯一确定。

凭借加网，才能从理论上消除印刷色彩的不确定性。同样，要取得既定的印刷呈色理论色调，非限定的加网不能实现。

2.1.2不同的加网方法产生不同的呈色效果

加网决定了分色后的理论色调，同时，不同的加网方法会产生不同的呈色效果[9]。如图2、图3所示，不同的加网方法会产生不同的各色版对应网点间微观上的叠合、并列份额，同样的色版面积率可能会形成不同的色元面积率，因而一般会表现出不同的呈色效果。同理，加网方法的各种参数中，任一参数(如加网角度、加网线数)的变化也都会引起色元面积率与色版面积率关系的变化，从而影响各个像素的理论色度。这就是说，理论呈色效果由加网方法及其参数唯一确定。

为了排除要素误差以及工艺过程误差(包括系统误差和随机误差)的影响，这里以理想过程、理想要素假设为前提，针对IT8.7/3标版的色标数据，基于表1所示实验条件，以方程(1)为依据，利用自编软件，对不同加网参数下的理论呈色效果进行仿真分析。

实验条件：D50的光源，150g铜版纸，2度视场。各色元x、y、z值见表1。

通过仿真计算和对比分析可知，同样的分色原稿，两种生长模型法产生的呈色结果不同，多数色块的色度值L*、a*和b*都存在差异。

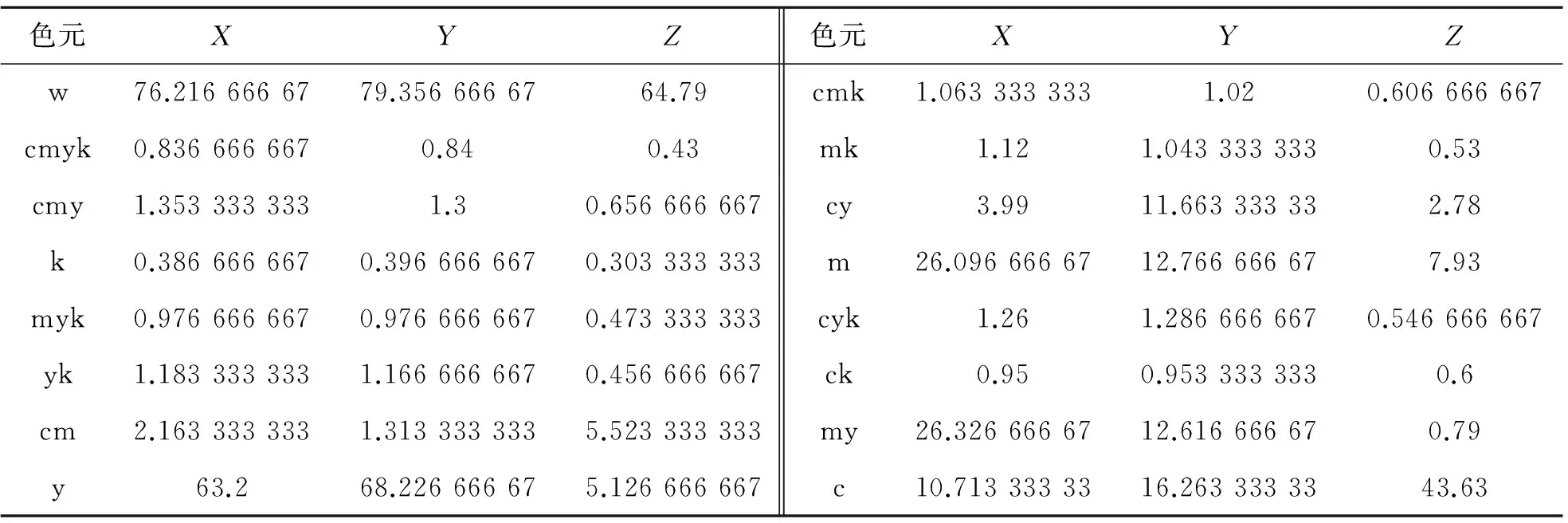
表1　 仿真分析实验条件

2.2理论色差与理论色调的加网依赖性

一般而言，不同的加网参数下，多数色块会产生不同的理论色度，那么，相较于既定的加网方法，也就必然会产生不同的理论色差。即理论色差具有加网依赖性。

2.2.1不同的加网参数会引起呈色相对色差

如2.1所述，加网决定了不同色版对应网点的相对几何关系，因而不同的加网方法以及具有不同加网参数(如加网角度)的相同加网方法都会产生不同的理论色度。这就是说，不同的加网方法(包括参数)之间必然存在着色差，虽然看上去不明显。那么色差几何呢？

因加网影响关系的复杂性，理论上定量归纳存在困难。这里仍采用仿真分析法说明这一问题。仍以图2、图3所示加网模板以及德米切尔(Demichel)网点模型为例，采用CIE1976Lab的标准总色差评价标准，进行呈色差异比较。部分结果示于图4。图中，横坐标为色块序号，纵坐标分别为CIE1976Lab标准总色差公式中的ΔL*、Δa*和Δb*。

从图4可以看出,无论明度、黄蓝轴色相还是红绿轴色相几乎在全色域内，不同的加网方法之间都存在着色相误差。

笔者早期也曾分析了三色印刷时，采用德米切尔网点模型进行分色，同时采用14个灰度级的生长模型法进行加网时的理论色差[16]。结果表明：在全部可以再现的2 744个色块中，只有168个色块不会产生理论色差，2 576个色块都会有不同程度的理论色差，达93.88%。可以证明：如果灰度级提高，这个比例还会上升。这表明，不同的加网之间总存在着色差，这一结论不具有偶然性。

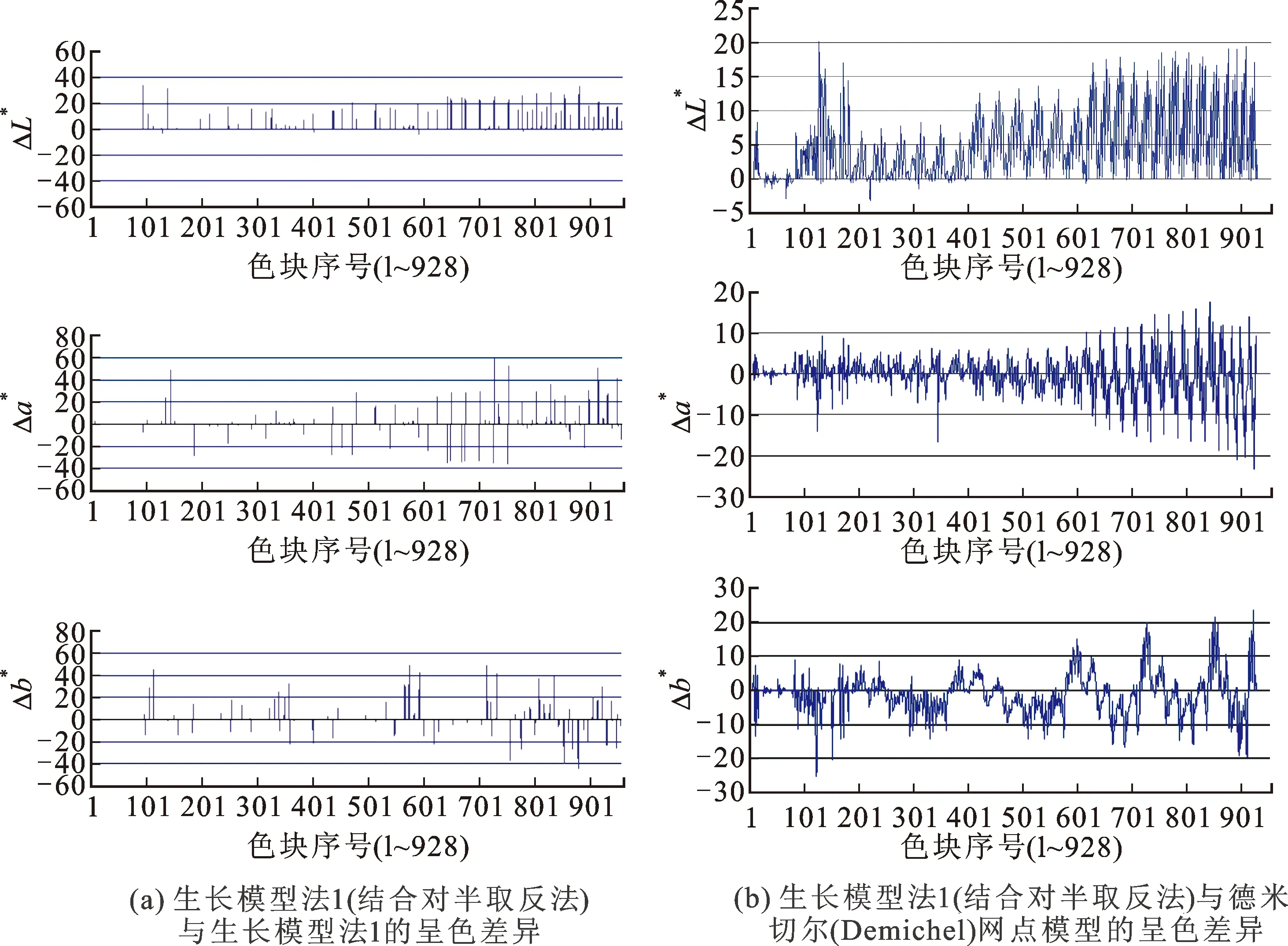
图4　不同加网方法的呈色差异比较Fig.4　The curves comparison of the CIE LAB diagram between different dot growth modles

2.2.2理论总色差随加网参数而变化

总色差的大小和变化趋势也具有加网依赖性。

理论分析和模拟仿真均可证明：采用不同的加网方式，两两之间均存在着理论色差，而且色差是变化的，不但随色彩空间的位置(即色度)的变化而变化，也随加网方法的变化而变化。这里列举其中三组仿真结果(见图5)。

从图5可看出，如果最合适的加网方法是生长模型法1，若采用生长模型法1(结合对半取反)加网，就会产生如图5(a)所示的理论色差；如果应该采用生长模型法1，若选择生长模型法2，就会产生图5(b)所示的理论色差；假如采用生长模型法1最贴近原稿，若采用了德米切尔网点模型，那必然会引入如图5(c)所示的系统误差。显然反过来结果同样成立。即如果把最适合的加网方法与所采用的加网方法两两对调，系统色差也是一样的。

上述分析表明：分色完成以后，采用不匹配的加网方式进行操作会引入系统误差。而且，该误差属于理论性的，除了具有变值性特点，即随色度变化而变化的本性外，还具有加网方式的依赖性。

这就是说，即使分色过程没有任何误差(包括模型误差、量化误差)，取得色版面积率c、m、y，通过加网也可能会产生色偏，因为这一过程引入了系统误差。

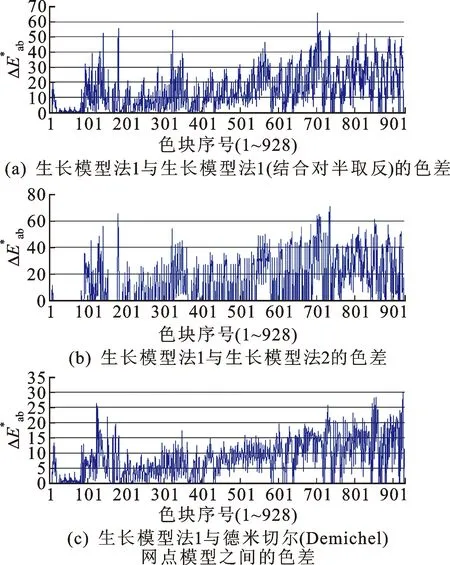
图5　不同加网方法之间的呈色总色差比较Fig.5　The curves comparison of the CIE LAB color differences between different dot growth modles

2.2.3理论阶调随加网参数而变化

前面考察了任意单一色块呈色效果(包括色差)的加网依赖性，其实，除了油墨三色外，其他中间色的理论色调也会因加网而变化，其阶调误差也具有加网依赖性。

这里暂且不考虑阶调压缩以及在实际印刷中由客观因素引起的阶调误差，仅仅考察因为加网而引起的阶调变化。也就是说，即使各色油墨单色阶调无需任何处理(即阶调复制曲线为45度直线)的条件下，仅仅因为加网处理，中间色彩的阶调就会产生一定的变化。

这里仍基于表1实验条件，采用色度体系CIE1931XYZ，对R(红)色梯尺的呈色(阶调)变化受加网形式的影响示于图6。从图6可看出：受制于单一色块呈色变化的加网影响机制，相对于理想阶调，不同加网方式都会引起阶调变化。这就表明：理论阶调也有加网依赖性。

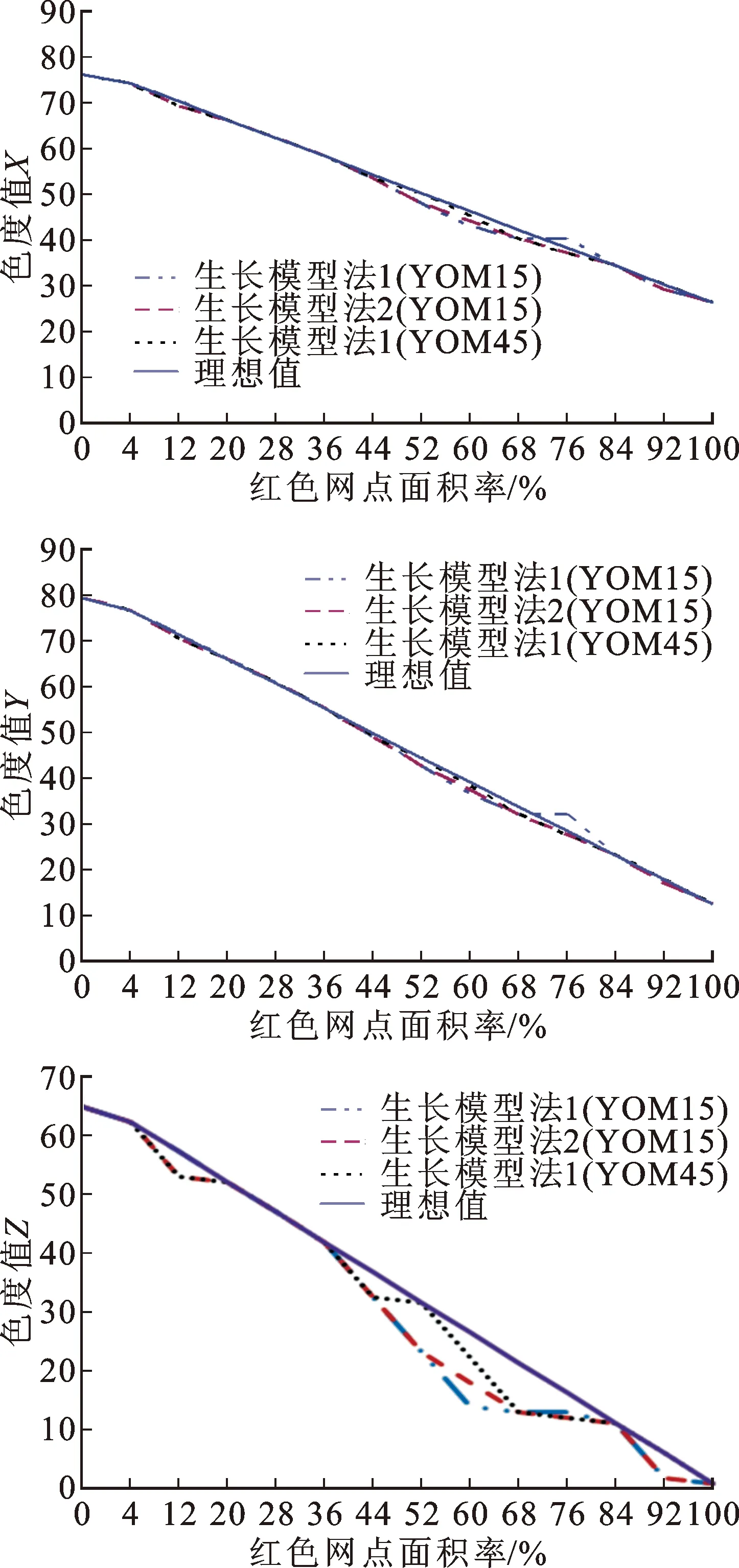
图6　不同加网方式下R(红)色梯尺的阶调变化Fig.6　The diagrams on the color scale (R) with different dot growth modles

2.3加网不具有独立性

诚然，为实现半色调彩色印刷，加网是必须的，但是决不能因为加网而改变既定色度，影响图像局部色相和整体色调。前述分析表明：不同的加网会获得不同的理论色彩。自由加网可能会破坏分色过程中限定的匹配色度。

2.3.1加网不具有任意性

分色时，原稿理论(基准)色度即已判定。然而，自由加网时印刷再现色度却会出现不确定现象。显然这是不允许的。通过简单的数学推理即可证明：加网不具有任意性。

理论上讲，色料呈色的色域可简单表示为一个六面体。在油墨色域六个边界面上(三个色版中，1个色版面积率为0%或100%)，每个网点(像素)只有不多于4个色元，显然此时不需要任何条件，凭借(1)式和(2)式即可正确、顺利完成分色。色元面积率和色版面积率都完全确定。那么，针对这些色彩的印刷，要忠实再现原稿，在选择加网方法时就应该照顾网点的既定叠合关系。可以想象，此时我们已经没有太大的选择余地，甚至根本就无可选择。

在较为简单的区域(色域边界)尚且如此，在更为一般的色域内，呈色效果具有更大的不确定性，自由加网根本不可能忠实再现原稿色彩。因为仅仅根据3个色版面积率要同时保证8个色元面积率不发生转移(变化)，尽管数学上有可能找到，而实际上目前所有的加网方法都不支持。由此可知加网不具有任意性。

2.3.2加网方法随分色过程而确定

不匹配的加网方式必然会引入系统误差。这种系统误差不但与加网方法有关，还具有变值特点，即不但随加网参数而变，而且随色彩位置而变。那么，如何才能在不同的加网方式之间找到最合适(即呈色效果与原稿无系统误差)的加网方法呢？只有采取了与分色相匹配的加网方式才不会引入系统误差。问题是，到底哪一种加网才能与分色匹配，保证不引入系统误差呢？其实，分色完成以后加网方式一般即已随之确定，不可任意选择。所谓与分色相适应，其实就是与分色时隐含的假定一致、或者与分色文件建立时的数据原稿(即色标印刷稿)的加网方式一致。

就忠实原稿而言，分色完成以后，加网方法即已固定。这就是加网对于分色的相关性。

3　分色的加网相关性

分色过程的核心内容包括选择分色方法、确定模型参数和分色操作三大过程。其中模型选取与参数确定过程，始终不能逾越加网的支持和影响。分色的加网相关性根植于方程(1)的求解困难，来源于分色方法(数学模型)的隐含假定以及建立模型时所依据的数据样本。

3.1分色物理模型的操作性问题

方程(1)描述了分色逻辑，是分色的物理模型，但同时也是数学模型。然可以证明，在CMY色空间中，只有一部分色彩可以直接利用公式(1)进行分色，这些色彩均位于6个色域边界面上，其他情况下则不能。因为在边界面上，属于任一色版为空的双色印刷或任一色版为实地的三色印刷，这些情况下均只生成4个色元，方程(1)可解。各色元面积率、从而各色版面积率可完全确定。

方程(1)具有不可求解的数学本质[8]告诉我们，给定(测得)了各色元色度值(Xi、Yi、Zi)以后，仅仅依靠它根本无法直接进行分色。因为无法确定各色元面积率fi，也就不能推知色版面积率。这其实也就是分色的困难所在。那么，要完成分色过程，解决操作性问题，就必须附加条件，使原方程降阶。为此业界进行了不懈的努力和尝试。这就是造成其相关性的本质根源。

实用中，无论采用那种分色方法，人们其实在不知不觉中，附加了条件和假定。

3.2分色模型的加网相关性

要进行分色，首先需要确定模型结构。不同的分色方法隐含着各自的条件假设。

基于色度匹配进行分色，目前主流的色彩空间转换方法包括：基于纽介堡方程、基于黑箱模型的变换方法以及基于查找表法等三类方法。这些方法虽具有不同的模型结构，但是均包含假定或附加条件，都需要加网条件的支持。

纽介堡方程分色方法，采用了德米切尔(Demichel)网点模型(假设)[8，15]，使原方程降阶，引入Coaxia模型也是一个尝试。关于纽介堡方程的各种修正或改良应用[10-13，17-19]也都一样，似乎不断有向好的研究成果出现，但始终没有跳出德米切尔方程的制约。由于给原模型(方法)增加了约束(可看作一种特定网)，并且其模型假设得不到可操作的加网方法的支持，必然造成系统误差[15-16]。笔者认为这也是纽介堡方程应用中的最大问题。

基于黑箱模型的变换方法，缺乏物理支持以及将系统误差归入随机误差处理，将分色过程看成是一个信息转化系统，忽视系统结构、假设转换模型(线性的或者非线性的)，然后采用数学方法进行输入输出关系拟合。黑箱模型目前有两类具体形式，即多项式回归和神经网络模型[2]。采用这类模型时，分色的正确性依赖于模型的正确性和参数的准确性，而参数的准确性又依赖于色标数据样本。

对于多项式回归模型，一般采用回归分析的方法确定其中的参数；而对于神经网络模型[2，7,11,19-20]，无论采用BP 神经网络模型，还是采用训练速度和泛化能力较高的基于径向基的RBF 神经网络分色模型, 都需要通过网络训练确定参数。为确定参数，他们都需要颜色样本空间。由加网的相关性可知，如果采用非印刷色标，本身就不可能正确再现原稿色彩，所以理论上讲色彩样本只能采用印刷色标。可是，如果采用印刷色标，就不可避免地掺入了加网信息。因为作为印刷品，色标在印刷时也是需要加网。对于同一个标版而言，不同的加网方法会生成不同的色标，而利用不同的色标就必然会得到不同的模型及其参数。这样，印刷色标中加网信息就造成了模型参数的加网相关性，也就导致了分色的加网依赖性。

查找表法[2，7,11]，应该说是迄今为止最好的分色方法，只是其操作性问题一直困惑着人们。查找表法的加网依赖性是很显然的，因为所有可实现的色彩数据都来源于包含加网信息的印刷色标。

3.3分色结果的加网相关性

这里采用简单的逻辑推理方法进行讨论。

在不考虑过程误差和要素误差的条件下，印刷呈色过程应该是可逆的。即原稿经分色取得分色原稿，加网印刷后应该得到与原稿(色度与色调)完全一致的印刷品。同样，如果以印刷品作为原稿进行分色，也应该会得到相同的分色原稿。

但是，这种可逆性是有条件的。一旦分色模型中隐含的加网信息与制版时采用的加网模型不一致，就不可能实现可逆化。

2.1节中的研究揭示：加网具有呈色效果的决定性。另一方面，分色方法(模型)具有分色结果的决定性。否则，信息传递的唯一性和正确性就没法保证。同样的分色稿，采用不同的加网方法和模型，会产生不同的理论呈色效果，即得到不同的印刷稿。显然，如果要让这些不同的印刷稿实现可逆，必然对应着不同的分色模型(参数)。

由此可以推知：同样的原稿，不同的分色方法和模型，必然产生不同的分色结果。之所以如此，是因为不同的分色方法和模型，包含着不同的网点生成模型或假设，隐含着不同的加网信息。一旦加网信息发生改变，分色结果就不可能保持一致。也就是说，分色结果具有加网相关性。

4　研究结论

以色彩的忠实复制为考量目标，基于色度平衡理念，以相对色差为判据，通过独立假设条件下工序理论色差的分析计算，揭示了分色与加网的相关性，但其相关性并不能解析表达和描述。研究(理论研究和仿真分析)结果显示：分色(采用某种方法)完成以后，除工艺因素影响外，理论上讲，印版传递的色彩特征，即复制色度受加网方法的左右，并不能完全确定；同样地，不同的分色方法及其模型的建立，也都离不开加网方法的支持。这表明，分色与加网相互依赖，互为前提，不具有相对独立性。分色方法一旦确定，加网方法随之确定，不具有任意选择性；同样，改变了加网方法(或假设)，分色模型及结果也会随之改变。

[1]胡成发.印刷色彩与色度学[M]. 北京：印刷工业出版社，1993.

[2]王强，刘全香，李治江.分色原理与方法[M]. 北京：印刷工业出版社，2007.

[3]姚海根. 数字加网技术[M]. 北京：印刷工业出版社，2000.

[4]章惠.色彩空间转换的理论和实证研究综述[J].包装工程，2011,32(13)：102-107.

ZHANG Hui. Review of academic and empirical research of color space conversion[J]. Packaging Engineering,2011,32(13)：102-107.

[5]KIM J.Color prediction of halftoning by modified Neugebauer Equations[C]//International congress of imaging science 2002，Tokyo(ICIS’02，Tokyo)：Imaging science and engineering creating the information technology of the Future).Portugal，2002：459-460.

[6]杜艳君，张逸新.经典彩色预测模型[J].包装工程，2006，27(2)：99-101.

DU Yanjun，ZHANG Yixin.Classical color prediction model[J].Packaging Engineering，2006，27(2)：99-101.

[7]李志会，唐万有，于治国.XYZ到CMY颜色空间转换的研究[J].包装工程，2010，31(7)：96-98.

LI Zhihui，TANG Wanyou，YU Zhiguo.Research on the conversion from XYZ to CMY color space[J].Packaging Engineering，2010，31(7)：96-98.

[8]成刚虎，王西珍.纽介堡方程应用误差的理论探析[J].西安理工大学学报，2011，27(1)：74-78.

CHENG Ganghu，WANG Xizhen.Application error analysis to Neugebauer Equation [J].Journal of Xi’an University of Technology，2011，27(1)：74-78.

[9]成刚虎，蒋艳丽，周薇.基于纽介堡方程的加网误差分析[J].中国印刷与包装研究，2012，4(1)：20-24.

CHENG Ganghu，JIANG Yanli, ZHOU Wei. Screening error analysis based on Neugebauer Equation[J].China Printing and Packaging Study，2012，4(1)：20-24.

[10]张琳，杨旭.纽介堡方程计算精度的研究[J].包装工程，2007，28(11)：73-74.

ZHANG Lin，YANG Xu.Research on precision of Neugebauer Equation[J].Packaging Engineering，2007，28(11)：73-74.

[11]周倩，刘真，朱明.3种主流分色算法的误差分析[J].包装工程,2011,32(7):107- 111.

ZHOU Qian, LIU Zhen, ZHU Ming. Errors analysis of three major color separation algorithms[J] . Packaging Engineering，2011，32(7)：107-111.

[12]张祯杰，刘真.3种基于分区纽介堡方程的分色算法的误差分析[J].包装工程，2012，33(15)：88-91.

ZHANG Zhenjie，LIU Zhen. Errors analysis of three color separation algorithms based on subarea Neugebauer Equation[J]. Packaging Engineering，2012，33(15)：88-91.

[13]SI Lili, LI Jincheng, JIANG Wenyan. Neugebauer model of a four-color inkjet printer[C]//Image and signal processing, 2009. CISP’09 2nd International Congress on. IEEE, 2009: 1-5.

[14]SI Lili, TIAN Xinli. Researche on Neugebauer equation correction algorithm[C]//Image and Signal Processing (CISP), 2010 3rd International Congress on. IEEE, 2010, 5: 2371-2375.

[15]成刚虎，熊康鹏.纽介堡方程的理论价值及其局限性分析[J].中国印刷与包装研究，2010，2(5)：24-28.

CHENG Ganghu，XIONG Kangpeng.Study on theoretical value and limitations of Neugebauer Equation[J]. China Printing and Packaging Study，2010,2(5)：24-28.

[16]成刚虎，张鸿，李云香. 纽介堡方程指数修正方法的理论剖析[J].西安理工大学学报，2015，31(1)：72-77.

CHENG Ganghu, ZHANG Hong, LI Yunxiang.Theoretical analysis of the index correction method of Neugebauer Equation[J].Journal of Xi’an University of Technology，2015，31(1)：72-77.

[17]司莉莉，刘真，刘浩学.纽介堡方程修正方法的研究[C]//第六届国际仪器仪表会议论文集.北京：北京理工大学出版社，2008.

[18]朱明，刘真，陈广学.基于分区纽介堡方程的6色印刷分色模型研究[J].光学学报，2011，31(7)：281-290.

ZHU Ming， LIU Zhen， CHEN Guangxue. Research on six-color separation model based on subarea Neugebauer Equations[J].Acta Optica Sinica，2011，31(7)：281-290.

[19]黎新伍.一种基于神经网络和 Neugebaure 方程的输入图像色彩校正模型[J].传感技术学报，2006，19(6)：2694-2698.

LI Xinwu.A color error correction model for input image based on neural natworks and Neugebauer Equation[J].Chinese Journal of Sensors and Actuators，2006，19(6)：2694-2698.

[20]黎新伍.一种基于BP神经网络和呈色原理的扫描仪色彩管理新模型[J].电子器件,2007,30(4)：1432-1435.

LI Xinwu. Scanner color management model based on BP neural network and color rendering principal[J]. Chinese Journal of Electron Devices, 2007,30(4)：1432-1435.

(责任编辑王卫勋,王绪迪)

Study on the correlation of separation and screening

CHENG Ganghu， LI Yunxiang， WU Jiao

(School of Printing，Packaging Engineering and Digital Media Technology,Xi’an University of Technology，Xi’an 710048, China)

For the modern color printing fields，halftone principle is the physical foundation, separation and screening is the core content in the process of color printing prepress processing. As the key and indispensable process,separation and screening has been regarded as (or assumed) two separate operations to carry out over the step operation in the industry for a long time.Thus system error introduced also have been overlooked. However, by considering relationship and influence of separation and screening, in this paper, we have confirmed formation of printing pixels and relationship of color information according to theoretical research and simulation analysis based on additive color shade. The results indicate: Screening method is determined with the separation process, separation model and the result because of screening methods (or assumptions) are changed. And consequently the results show that: separation and screening is theoretically relevant and does not have a mutual independence.

separation; screening; relatirity; system error

1006-4710(2016)02-0218-08

10.19322/j.cnki.issn.1006-4710.2016.02.015

2015-11-21

陕西省教育厅专项科研计划研究资助项目(2010JK706)

成刚虎，男，教授，研究方向为印刷系统工程。E-mail:chenggao@xaut.edu.cn

TS801.3

A