基于粒子群优化算法的永磁同步电机H∞速度观测器

朱　群， 尹忠刚， 张延庆， 钟彦儒

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)



基于粒子群优化算法的永磁同步电机H∞速度观测器

朱群， 尹忠刚， 张延庆， 钟彦儒

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

H∞速度观测器实现了对永磁同步电机矢量控制系统的转速估计。然而，观测器中加权矩阵的选取费时费力，从而限制了其在高性能变频调速系统中的应用。为了解决上述问题，本文提出了一种基于粒子群优化算法的永磁同步电机H∞速度观测器。该方法在H∞速度观测器矢量控制系统的基础上引入粒子群优化算法，并在文中给出了算法的实现方式。仿真结果证明：基于粒子群优化算法的永磁同步电机H∞速度观测器进一步提高了永磁同步电机无速度传感器矢量控制系统的控制性能，同时具有更好的动态性能和抗干扰性能。

粒子群优化算法； 永磁同步电机； H∞速度观测器； Riccati方程

在高性能交流调速控制系统中，光电编码器、旋转变压器等机械传感器检测到的信号需要参与磁场定向运算，然而，这样高分辨率的传感器增加了系统成本，降低了系统可靠性，也限制了其应用范围。虽然矢量控制已用于PMSM，但是传统的开环模型方法仍存在很多不足。因此学者们提出了很多先进的转速估计策略，主要有[1-5]模型参考自适应法[1]、非线性观测器、高频信号注入法[3]、滑模观测器法[4]以及扩展卡尔曼滤波器法[5]。

1981年，学者Zames提出了H∞控制理论，如今已成为控制理论领域的研究热点，其应用研究涉及电力系统、电力电子、航空和航天等领域[6-10]。在交流电机调速系统当中，H∞鲁棒控制理论多作为系统控制器应用[11-12]，然而，本文将H∞鲁棒控制理论应用于系统的状态估计，提出了一种H∞速度观测器。首先在永磁同步电机基本数学模型的基础上建立了增广被控对象的状态空间方程，然后证明及推导得到观测器给定值的数学表达式，通过求解Riccati方程，得到H∞速度观测器。

在观测器的实现过程中，通过直接计算很难得到待定参数q1、q2、q3和r的取值，从而使系统无法获得最优的控制性能。因此,本文将粒子群优化算法(PSO)[13-15]应用到参数优化部分，从而提高了系统的动态性能和抗干扰性能。最后通过仿真构建基于PSO的H∞速度观测器PMSM矢量控制系统，验证了所提方法的可行性和有效性。

1　基于H∞观测器的PMSM转速估计方法

1.1PMSM数学模型的建立

引入同步旋转坐标系，在d-q坐标系下的PMSM的定子电压可表示为：

(1)

式中，ud、uq、id、iq分别表示电机d、q轴电压分量与电流分量，ωe表示转子电角速度，λm表示永磁体磁链，Rs表示定子电阻，Ld、Lq分别表示定子d、q轴等效电感，并且对于内埋式PMSM，有Ld≠Lq。

电机的电磁转矩为：

Te=1.5p[(Ld-Lq)id+λm]iq=Ktiq

(2)

式中，Te表示电机的电磁转矩，p表示电机极对数，Kt表示转矩常数。电机的机械运动方程表达式为：

(3)

(4)

由式(2)～式(4)可以推导得到永磁同步电机的数学模型：

(5)

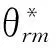
定义系统的动态性能评价信号：

z=C1x+D11w+D12v

(6)

其中，变量z为评价函数，C1和D12为加权矩阵，qi> 0 (i=1, 2, 3)和r>0为加权系数，可通过改变加权系数取值获得最优的性能。其中，C1调节了系统干扰抑制效果，D12影响着控制输入的大小。

假设系统的观测量y同系统的状态变量x相等，则输出方程为：

y=C2x+D21w+D22

(7)

式(5)～(7)为基于H∞控制理论的增广被控对象的状态空间方程[16]，由此可以得到增广矩阵G：

(8)

1.2基于粒子群优化算法的H∞速度观测器

对于图1所示的鲁棒观测器模型，要求设计一个状态观测器的反馈增益矩阵K，使得整个闭环系统渐近稳定，且从系统输入信号w到输出信号z的闭环传递函数Tzw的H∞范数不超过一个给定的上界γ，以确保系统对由w进入的不确定性因素具有鲁棒稳定性。其中，观测器对应的K可由被控对象的增广矩阵G求得。本文所设计的H∞鲁棒观测器旨在估计PMSM的转速。

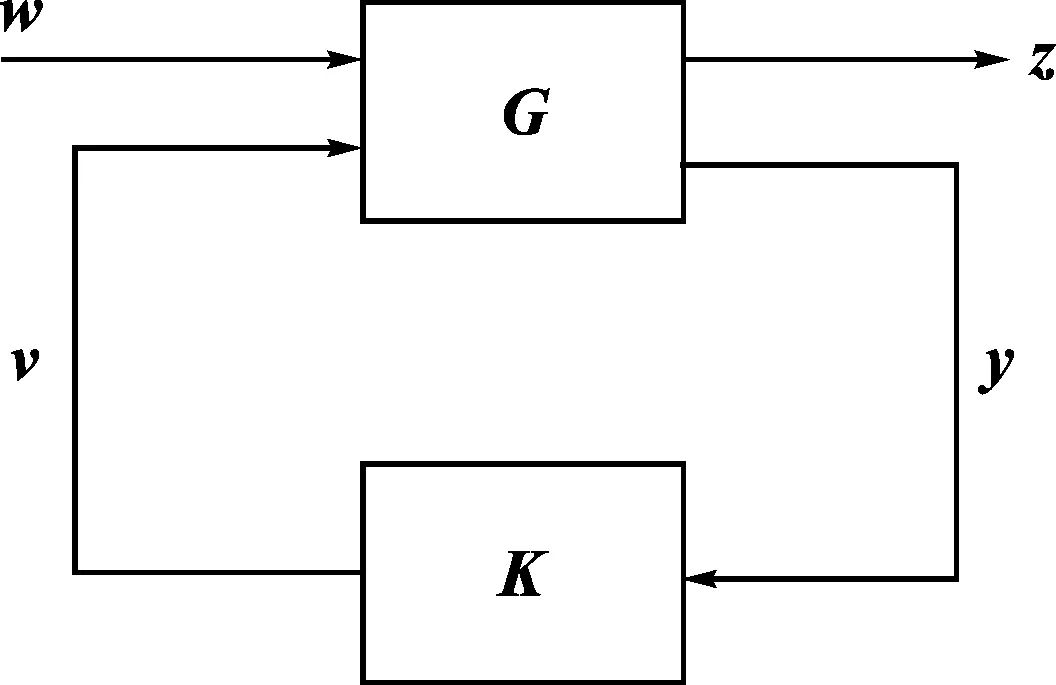
图1　H∞鲁棒观测器模型Fig.1　Model of H∞ robust observer

根据上述分析可知，系统从输入w到输出z的传递函数为[17]：

Tzw=(C1+D12K)(SI-A-B2K)-1B1

(9)

式中，S为微分算子，I为3阶单位阵。

当给定上界γ > 0，H∞状态反馈观测器存在的充要条件为：

‖Tzw‖=‖(C1+D12K)

(SI-A-B2K)-1B1‖<γ

(10)

有约束条件的极值问题，可通过Lagrange乘子法转化为无条件的极值问题。设Lagrange乘子为λT，则有优化性能指标：

(11)

本文通过寻求一个正定矩阵P，使电机从初始时刻(t=0)的初始状态转移到末值时刻 (t=td)的终止状态，满足性能指标J为最小，从而得到哈密顿函数[18]：

(12)

通过求解式(12)，可获得不等式：

(13)

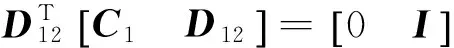
(14)

通过求解以上Riccati方程可以得到正定矩阵P。代入状态观测器的反馈增益矩阵K的数学表达式，可以获得永磁同步电机H∞速度观测器的反馈信号：

(15)

由式(15)可以看出，控制输入信号v与状态变量x、正定矩阵P及非受控对象的参数阵B2、C1和D12有关。

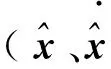
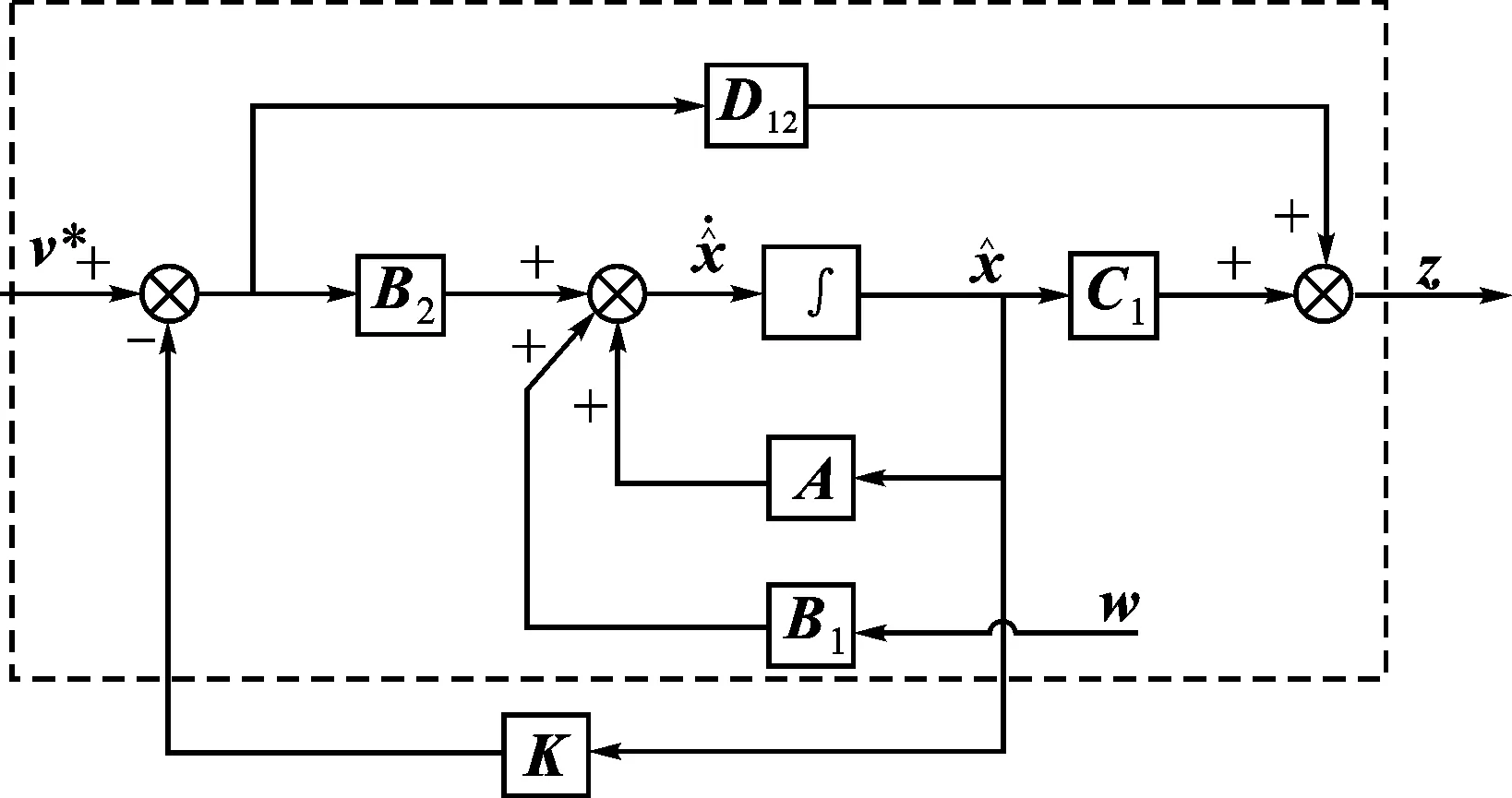
图2　H∞鲁棒观测器的结构图Fig.2　Speed estimation block of H∞ robust observer

在满足H∞鲁棒控制的条件下获得性能指标J(如式(11)所示)最小的观测器是一个费时费力的过程，直接计算参数难以得到最优系统，因此，本文采用粒子群优化算法(PSO)寻找观测器最优参数，从而提高系统性能。

粒子群优化算法模拟鸟类捕食行为，算法中每个粒子都代表问题的潜在解，每个粒子对应一个由适应度函数决定的适应度值。粒子的速度决定了粒子移动的方向和距离，速度随自身及其他粒子的移动经验进行动态调整，从而实现个体在可行解空间中的寻优。

本文对Riccati方程中的q1、q2、q3、r应用PSO算法进行参数整定和优化。

第一步：粒子的位置设为Q=(q1, q2, q3, r)T。

第三步：采用PSO的位置和速度公式更新第k拍粒子的位置。

(16)

(17)

第四步：采用MATLAB指令求解粒子新位置对应的P矩阵，获得此时系统的估计转速。通过得到的转速误差判定pbestin和gbestin的更新。

第五步：从pbestin和gbestin的最优值求出最优H∞鲁棒观测器，输出电机的估计转速，反馈给转速PI调节器，驱动永磁同步电机系统稳定运行。

2　仿真验证

为了验证H∞鲁棒观测器的有效性, 利用MATLAB软件对系统进行仿真。仿真采用变步长，模式选为ode45，采样时间间隔为62.5 μs (16 kHz)。PMSM参数如表1所示。

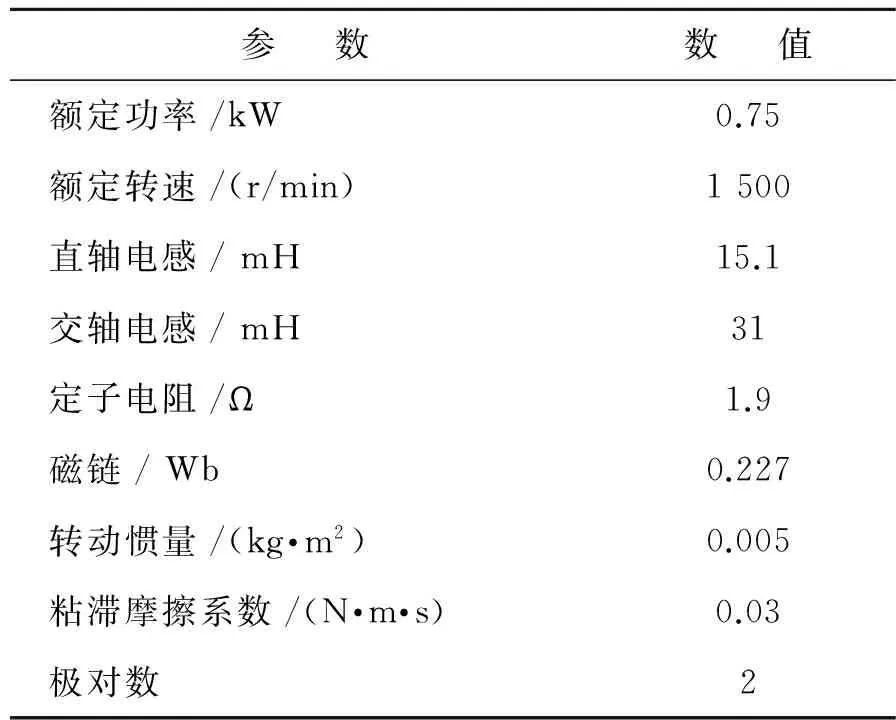
表1　永磁同步电机参数

图3为基于粒子群优化算法的H∞鲁棒观测器PMSM矢量控制系统框图。

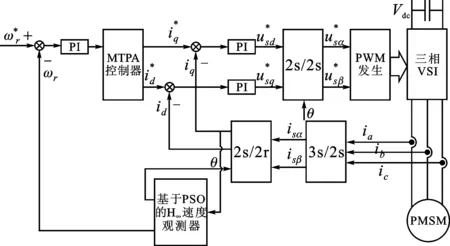
图3　基于PSO的H∞鲁棒观测器PMSM矢量控制系统Fig.3　Block of the H∞ robust observer PMSM vector control system based on PSO

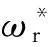
经过30次迭代，得到PSO寻优中H∞鲁棒观测器各参数的变化曲线图，如图4所示。

由图4可以看出，从3个随机赋值开始，经过7次迭代后，寻优曲线达到最低点，迭代12次后，曲线的变化趋于稳定。最终得到的最优观测器参数为q1=8、q2=8.5、q3=10、r=0.012。

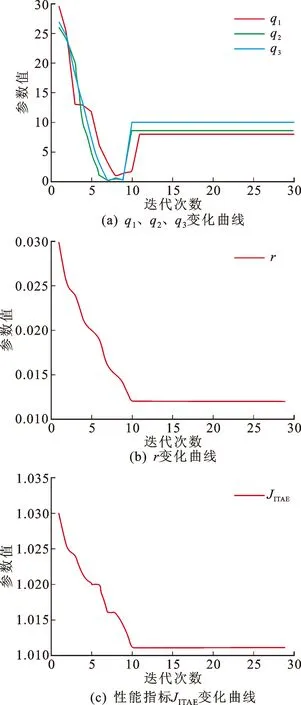
图4　PSO寻优中H∞ 观测器各参数的变化曲线Fig.4　Parameters wave of H∞ robust observer by PSO algorithm

将寻优得到的数值代入式(15)，调用MATLAB指令求取P矩阵，从而获得基于粒子群优化算法的状态反馈增益矩阵K：

(16)

由此可以得出基于PSO寻优的H∞转速观测器。为了验证该观测器的正确性，现从空载启动和稳态加载两个方面进行分析。

当电机空载启动至额定转速时，比较H∞转速观测器估计转速和PSO寻优得到的H∞转速观测器估计转速，如图5所示。可以看出，经过大约0.018 s，转速稳定至1 500 r/min，表明观测器的估计值在额定转速上可以良好地跟踪实测转速。另一方面，由粒子群优化算法得到的H∞转速观测器保证了参数选择的合理性，能够很好地估计出电机实测转速。

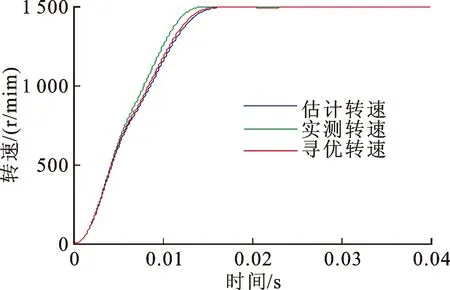
图5　起动时的转速比较曲线Fig.5　Speed comparison waveforms when start-up

令电机在额定转速上空载启动，运行至0.05 s时，突加2.5 Nm负载，继续运行至0.08 s时，加载1 Nm短时负载扰动，绘制这个过程中的转速变化曲线，如图6所示。

从图6可以看出，基于PSO的H∞速度观测器在加载和负载扰动的情况下都能够迅速恢复到给定值上，抗干扰性能良好。

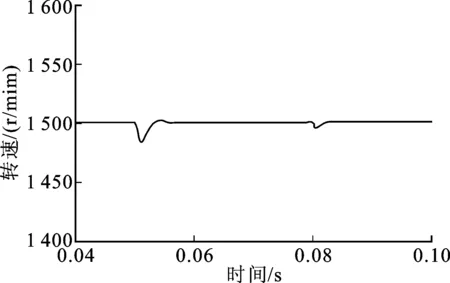
图6　加载情况下H∞ 观测器转速估计曲线Fig.6　H∞ robust observer estimation speed with load

3　结　语

H∞速度观测器能够对永磁同步电机的转速进行准确的估计。观测器中加权系数的确定对其性能有重要影响，本文将粒子群优化算法引入到H∞鲁棒观测器中，通过该算法离线寻优观测器的加权系数，并将由此得出的观测器置于永磁同步电机矢量控制系统上进行了仿真研究，结果表明，H∞观测器在加载和负载扰动两种工况下都能够实现对电机转速的准确估计，同时表现出良好的抗干扰性能。

[1] 齐放, 邓智泉, 仇志坚. 基于MRAS的永磁同步电机无速度传感器[J]. 电工技术学报, 2007, 22(4): 53-58.

QI Fang, DENG Zhiquan, QIU Zhijian. Sensorless technology of permanent magnet synchronous motors based on MRAS [J]. Transactions of China Electro Technical Society, 2007, 22(4): 53-58.

[2]ZHANG Xiaoguang, SUN Lizhi, ZHAO Ke, et al. Nonlinear speed control for PMSM system using sliding- mode control and disturbance compensation technique [J]. IEEE Transactions on Power Electronics, 2013, 28(3):1358-1365.

[3]秦峰, 贺益康, 贾洪平. 基于转子位置自检测复合方法的永磁同步电机无传感器运行研究[J].中国电机工程学报,2007,72(3):12-17.

QIN Feng, HE Yikang, JIA Hongping. Investigation of the sensorless control for PMSM based on a hybrid rotor position self-sencing approach[J]. Proceedings of the CSEE, 2007, 72(3): 12-17.

[4]SONG Chi, ZHANG Zheng, XU Longya. Sliding mode sensor less control of direct-drive PM synchronous motors for washing machine applications [J]. IEEE Transactions on Industry Applications, 2009, 45(2): 582-590.

[5]YIN Zhonggang, ZHANG Ruifeng, ZHONG Yanru, et al. Speed and flux estimation of permanent magnet synchronous motor for sensorless vector control based on robust extended kalman filter[C]// Industrial Electronics (ISIE), 2012 IEEE International Symposium on. Hangzhou, 2012: 748-751.

[6]张辉, 谭国俊, 钱苗旺，等. 基于H∞控制与最优跟踪控制相结合的三相PWM整流器控制策略[J]. 电工技术学报, 2012, 27(12): 102-108.

ZHANG Hui, TAN Guojun, QIAN Miaowang, et al. Study of three-phase PWM rectifier based on a mixture of H∞control and optimal tracking control [J]. Transactions of China Electro Technical Society, 2012, 27(12): 102-108.

[7]李鹏, 杨以涵. 电能质量的H∞最优控制方法[J]. 电工技术学报, 2005, 20(10): 88-102.

LI Peng, YANG Yihan. H∞optimization control method of power quality [J]. Transactions of China Electro Technical Society, 2005, 20(10): 88-102.

[8]魏立新, 李二超, 王洪瑞. 基于混合优化神经网络的机器人力/位置控制[J]. 电机与控制学报, 2006, 10(2): 151-154.

WEI Lixin, LI Erchao, WANG Hongrui. Hybrid force/position control based on mixed optimal neural networks[J]. Electric Machines and Control, 2006, 10(2): 151-154.

[9]梁宵, 王宏伦, 盖文东.飞行器不确定性建模与μ-H∞鲁棒动态逆控制[J].控制与决策,2012,27(7):1066-1071.

LIANG Xiao, WANG Honglun, GAI Wendong. Uncertainty modeling andμ-H∞robust nonlinear dynamic inversio n control of aircraft [J].Control and Decision, 2012, 27(7): 1066-1071.

[10] 聂子玲, 马伟明, 李卫超，等. 矢量控制感应电动机H∞磁通观测器研究[J]. 电工技术学报, 2006, 21(8): 31-36.

NIE Ziling, MA Weiming, LI Weichao，et al. H∞flux observer of induction motor for vector control [J]. Transactions of China Electro Technical Society, 2006, 21(8): 31-36.

[11]LONG Bo, CHENG Yongqiang. H∞robust controller design for regenerative braking control of electric vehicles [C]// Industrial Electronics and Applications (ICIEA), 2011 6th IEEE Conference on, Beijing, 2011: 215-219.

[12]祖晖, 章国宝, 费树岷，等.基于不确定广义模型的永磁同步风力发电机鲁棒H∞控制 [J]. 控制理论与应用, 2011, 28(11): 1634 -1640.

ZU Hui, ZHANG Guobao, FEI Shumin, et al. Robust H-infinity control for permanent-magnet synchronous generators in wind-energy conversion system based on uncertain descriptor model [J]. Control Theory & Application, 2011, 28(11):1634-1640.

[13]钱苗旺. 基于粒子群优化算法的永磁同步电机H2/H∞混合控制[J]. 计算机应用. 2012, 32(8):2381-2384.

QIAN Miaowang. Mixed H2/H∞control of permanent magnet synchronous motor based on particle swarm optimization algorithm [J]. Journal of Computer Applications, 2012, 32(8) : 2381-2384.

[14]姬军鹏, 华志广, 胡雪利, 等. 基于PSO的无源电力滤波器支路拓扑的优化设计[J]. 西安理工大学学报. 2014, 30(2): 231-237.

JI Junpeng, HUA zhiguang, HU Xueli，et al. Optimal design of branch topologies of passive power filter based on PSO [J]. Journal of Xi’an University of Technology，2014, 30(2): 231-237.

[15]CAO Shaozhong，TU Ji，LIU Heping. PSO algorithm based robust design of PID controller for PMSM [C]// Natural Computation (ICNC), 2010 Sixth International Conference on，Yantai, Shandong, 2010: 3513-3517.

[16]CHEN J L, LIU T H, CHEN C L. Design and implementation of a novel high-performance sensorless control system for interior permanent magnet synchronous motors [J].IET Electric Power Applications., 2010, 4(4): 226-240.

[17]林立, 黄苏融. 永磁同步电机系统线性化H∞鲁棒控制[J]. 电机与控制学报, 2009, 13(4): 541-547.

LIN Li, HUANG Surong. Robust control with lineari- zation technique for interior permanent magnet synchronous motor servo system [J]. Electric Machine and Control, 2009, 13(4): 541-547.

[18]朱群, 尹忠刚, 钟彦儒. 基于鲁棒H∞观测器的永磁同步电机转速估计方法[J]. 电力电子技术, 2015, 49(5): 31-35.

ZHU Qun, YIN Zhonggang, ZHONG Yanru. Speed estimation of permanent magnet synchronous motor based on robust H∞observer[J]. Power Electronics, 2015, 49(5): 31-35.

(责任编辑周蓓)

H∞speed observer of permanent magnet synchronous motor based on particle swarm optimization algorithm

ZHU Qun， YIN Zhonggang， ZHANG Yanqing， ZHONG Yanru

(School of Automation and Information Engineering，Xi’an University of Technology，Xi’an 710048， China)

The speed estimation of the permanent magnet synchronous motor (PMSM) vector control system is realized by using H∞speed observer. But its control performance has a relationship with weight coefficient directly, so that its application of high-performance is influenced in the variable frequency system. A novel method for using H∞speed observer of permanent magnet synchronous motor based on particle swarm optimization algorithm (PSO) is proposed in this paper, with the PSO algorithm studied on the basis of the H∞speed observer vector control system and the algorithm realization analyzed. The PSO algorithm is introduced to the H∞speed observer, and the observer coefficient is optimized by taking full advantage of the adaptability of PSO algorithm. The simulation results verify that the performance of PMSM sensorless vector control system is better.

particle swarm optimization algorithm； permanent magnet synchronous motor； H∞speed observer； Riccati equation

1006-4710(2016)02-0207-06

10.19322/j.cnki.issn.1006-4710.2016.02.013

2015-05-10

国家自然科学基金资助项目(51307139)；陕西省工业攻关资助项目(2014K06-29)；陕西省教育厅专项基金资助项目(2013JK0998)

朱群，女，博士生，研究方向为高性能交流调速系统与电力电子变换器数字化控制。E-mail: zhuqunsmile@163.com

钟彦儒，男，教授，博导，研究方向为电力电子交流传动系统与变频器。E-mail:zhongyr@xaut.edu.cn

TM71

A