内河航道船舶交通流动力模型研究

鲍业辉，杨海飞

（1.苏交科集团股份有限公司，江苏 南京 210017；2河海大学，江苏 南京 210098）

内河航道船舶交通流动力模型研究

鲍业辉1，杨海飞2

（1.苏交科集团股份有限公司，江苏 南京 210017；2河海大学，江苏 南京 210098）

通过研究传统交通流模型的跟驰理论，发现其简化过程无法考虑船型尺寸分布、船舶动力、水面阻力等复杂的船舶航行条件。为克服上述限制条件，增加粘性阻力项建立船舶跟驰模型，将跟驰模型中的微观参量转换为宏观参量，建立船舶交通流动力模型，对交通流模型进行了数值离散。模拟结果表明船舶交通流动力模型能够再现各种交通扰动波的传播情况，具有较好的适用性。

船舶交通流；动力模型；内河航道；数值仿真；粘性阻力

1 概述

随着内河航道船舶交通量不断增加，船舶趋向大型化、高速化，航道出现了严重拥堵现象。为改善航道交通状况，保障船舶航行安全，有必要对河航道船舶交通流模型进行开发和评估。

对内河航道交通流模型的研究起步较晚，现有的研究主要限于借助道路交通流模型的基本方程。船舶交通工程学认为，船舶交通流的基本方程可表示为交通量等于交通流速度、交通流密度以及交通流宽度的乘积［1］。但水上交通工程与道路交通工程存在交通工具和交通设施的巨大差异，船舶交通流的基本方程不能全面反映船舶流随时间和空间变化而变化的规律。近年来，部分学者借鉴交通流动力学理论讨论船舶交通流模型，分析船舶流的一些特征［2］。但到目前为止，此类研究仅仅采用了守恒方程，即一阶连续模型，而没有考虑由于船舶外形尺寸、动力特性等不同而产生的船舶相互之间的加速度和惯性影响以及船舶在水域中航行所受的阻力作用［3-4］。因此，该模型不能完整反映非均衡状态交通流的动力学特性。针对以上船舶交通流的研究不足，本文结合内河航运的特点，从微观船舶跟驰模型出发，通过将微观参量转化为宏观参量，建立船舶交通流动力模型，并对不同扰动下的交通波传播情况进行数值模拟，以再现一些常见的水上交通现象。

2 船舶跟驰理论模型

道路车辆交通流动力学模型大多都是基于车辆跟驰模型演化而来，跟驰模型是基于反应-刺激的关系，可以用方程式表示为：

反应=λ·刺激

在车型较为单一的车流情况下，各车的制动距离近似相等，从而推导出经典的线性跟驰模型［5］。但对于船舶交通流，由于船型尺寸、动力特性等差距都很大，相邻船舶的制动距离假设相等是不符合实际的。本文考虑不同船型分布情况下的船舶制动距离差，结合文献［6］ 提出的广义跟驰模型，推导得到船舶跟驰模型：其中：

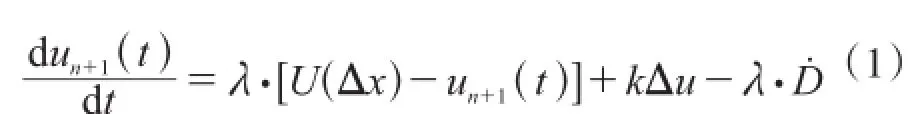
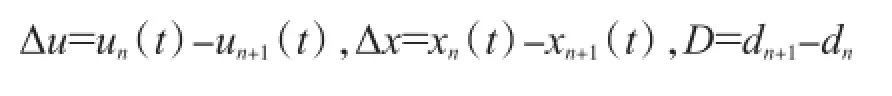
式中： un和un+1分别为头船和跟驰船舶的速度T为弛豫时间；k为反应系数；U为Δx的函数，Δx为前后两船舶的位移差；dn、dn+1分别为头船与跟驰船的制动距离；D为相邻船舶之间的制动距离差；为船舶交通流的粘性阻力项，是关于船型分布、船舶流密度、航行速度、船舶领域、相关航道技术指标、时间t的函数，粘性阻力项定义为：

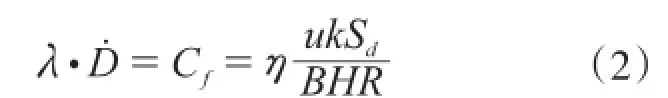
式中：η为粘性系数，与船型分布有关，若船型尺寸服从正态分布，则η是关于分布标准差的增函数即船型混合比例越高，船型越复杂，粘性系数值越大；u为船舶航行速度，速度越大，相邻船舶的制动距离差越大，阻力越大；Sd为船舶领域［7］，它是船舶在航行过程中所需要的安全缓冲领域；B、H、R分别为航道通航宽度、航道通航深度以及航道转弯半径。

3 船舶跟驰模型

3.1 船舶交通流动态模型

将方程（1）中的微观参量转换为宏观参量，令：un+1（t） ～u（x，t），un（t） ～u（x+Δx，t），U （Δx）～ue（k），，其中：T为弛豫时间，τ为扰动向后传播Δx距离所需时间，u（ek）为船舶流密度和速度的平衡关系式。令 λ˙D˙=Cf，将上述参量转换代入船舶跟驰模型关系中，并将右边项进行Taylor展开，只保留线性项，得到：

同时，船舶交通流应满足守恒方程：

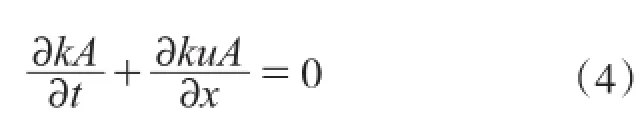
式中：A为船舶流航迹带宽度。

方程（3）和（4）构成了船舶交通流动力学模型。对由方程（3）和（4）组成的方程组进行特征线分析，得到特征速度：

由于扰动传播速度ω0＞0，则该船舶交通流动力模型中不存在大于宏观车流速度的特征速度，符合实际船舶流情况。

采用该模型对Draganzo C F［8］提出的交通流倒流问题进行分析，该问题的初值条件为：

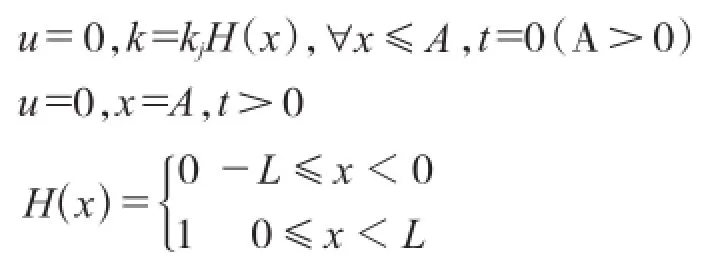
式中：H（x）是Heaviside函数，kj为阻塞密度。这样的条件描述了一种特殊的交通状态，交通处于停止队列状态（如前方出现船闸），且后方没有船舶加入队列的情况（上游船闸停止调度船舶）。此时，船舶流应保持原有状态，即：

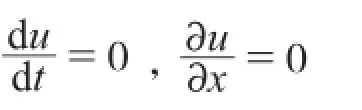
将上述两方程代入方程（3），得到：

因此，u≥0恒成立，即该船舶交通流动力模型中不会出现船舶倒退问题。

3.2 相关参数验证

（1）船舶交通流密度k

船舶流密度即船舶的空间密集度，对于已定线的内河航道，可定义为在一条航迹带宽度内，单位长度航道上的船舶艘数，可以通过出入量和摄影法调查得到。下面就出入量法做一简介：选取一段两断面间无出入交通的长为L的航段，在两端A、B两点分别设置观察点，船舶从A驶向B，如图1（a）所示，观察开始（t=t0）时，AB航段内存在的初始船舶数为N（t0），从A驶入的船舶数为A（t0），从B驶出的船舶数为B （t0），t时刻内从A驶入的累计船舶数为A（t），从B驶出的累计船舶数为B（t），若N（t0）+B（t0）-A（t0）=0，则t时刻AB航段内存在的船舶数应为初始船舶数和t时刻内AB航段的船舶数改变量之和。即：

N（t）=N（t0） +（A（t）-A（t0））-（B（t）-B（t0））=A（t）-B（t），

则密度为：k（t）=N（t）/L。

当选取的航道L比较短，观察时间间隔t比较小时，可以引入微分来表示航段x位置的船舶密度：

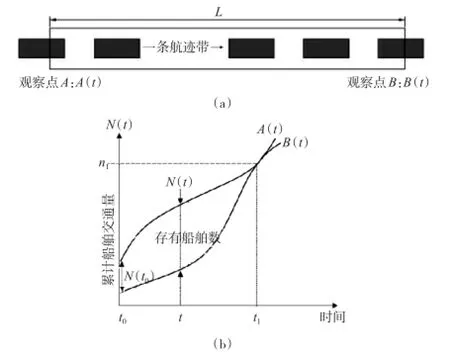
图1 AB航段船舶数量与累计船舶交通量图示

（2）船舶交通流平衡速度

文献［9］认为船舶交通流的密度与速度呈分段线性关系：

式中：uf为船舶畅行速度；k为船舶交通流密度；ks为船舶交通流临界密度；kj为船舶交通流阻塞密度。

（3）弛豫时间（slack time）T

弛豫时间是是指交通状态改变时，驾驶员反应到执行船舶速度调整达到平衡状态的时间，它由反应时间和执行时间两部分构成：

T=Tr+Te

反应时间Tr是驾驶员感知到交通状态变化的时间；执行时间Te则是在感知到交通状态变化到执行调整操作至达到平衡状态的时间。

（4）粘性阻力Cf

粘性阻力项Cf的定义同上文所述。

4 数值模拟

4.1 数值计算法

对时间采用前差分，对空间采用中心差分，构造守恒方程（3）的差分格式：

对于动力学方程（4），本文应用迎风差分法来求得数值解，具体的差分格式为：

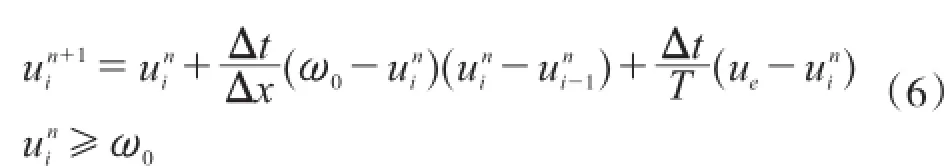
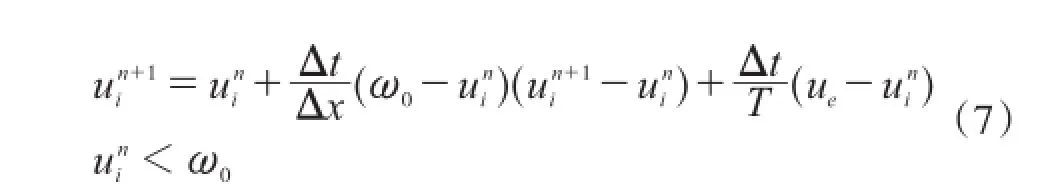
4.2 实例分析

（1）下游航段变窄模拟结果分析

下游航段变窄在船舶交通流特性上表现为下游密度高于上游。设置源项扰动密度稍大于临界密度，交通流密度图（见图2）显示，后半部分密度波只向后传播，而不向前传播。在实际交通流中，可以解释为因前方船舶流密度较大而出现船舶积压，上游航段因下游密度波和源项密度波扰动的影响，密度波扰动幅度随时间推移不断增大，相应的速度也出现一定的高低起伏变化，特别是在两密度波交界处，速度波动最大，主要是临界密度附近交通流处于不稳定状态。

图2 下游水道变窄时的密度变化

（2）下游航段变宽模拟结果分析

下游航段变宽在船舶交通流密度上表现为下游密度值较上游小。分别在两部分航段设置不同的中高密度值（均高出临界密度），前半部分密度初始值高于后半部分初始值，交通流源项扰动密度略高于前半部分密度值。交通流密度时空图（见图3）显示前半部分交通流密度波随时间的推移既会向前传播，也会向后传播，向后传播的速度大于向前传播的速度，扰动传播有衰减趋势。

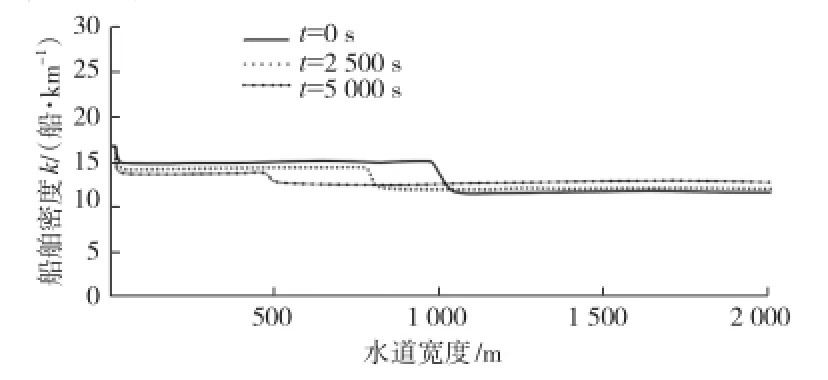
图3 下游水道变宽时的密度变化

（3）瓶颈航段模拟结果分析

瓶颈航段反映在密度上即航段航道的密度高于周围两边航段的密度值。设置瓶颈航段的密度值比周围两边航段的密度值高，刚开始速度为畅行速度，船舶交通流时空变化图（见图4）显示，瓶颈航段的密度波会随着时间推移向前后传播，大约在3 000 s后，向后传播的密度波和航段起始源项向前传播的密度波汇合，出现复杂的非线性现象，

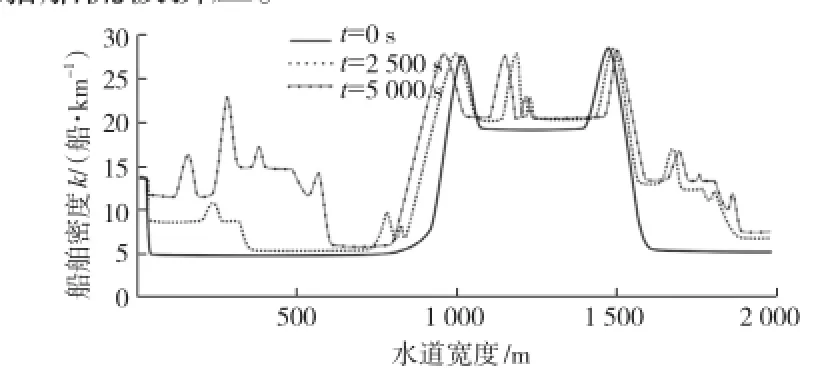
图4 水道瓶颈时的密度变化

数值模拟结果表明，本文建立的船舶交通流动力模型能够较好地模拟不同扰动情况下的交通波传播等常见的水上交通现象，具有很好的适用性。

5 结论

本文在研究传统跟驰模型推导过程中，发现其简化过程无法考虑船型尺寸分布、船舶动力、水面阻力等复杂的船舶航行条件。通过增加粘性阻力项克服以上缺陷，建立了船舶跟驰模型；将微观参量转换为宏观参量，应用动力学方法建立了船舶交通流动力模型；对交通流模型进行了数值离散，模拟结果表明船舶交通流动力模型能够再现各种交通扰动波的传播情况，具有较好的适用性。论文的突出创新在于建立了船舶交通流方程的广义粘性阻力项，利用一些宏观参数组合的函数来表达船舶流前进中的广义阻尼，是解决诸多微观阻尼在方程中无法表达的可靠方法。但粘性阻尼项的形式论证尚不够充分，目前虽有线性的标定系数，但各因素间的相互比例关系不精确会造成实际误差没法评估的情况。论文后期将通过实测数据标定合理的粘性项，完善粘性项的研究，进一步完善船舶交通流动力模型。

［1］邱民.船舶交通工程学［M］.北京：人民交通出版社，1992.

［2］Shao C F，Fang X L. Fluid model of vessel traffic flow［J］. Journal of Dalian Maritime University，2002，28：52-55.

［3］Lighthill M J， Whitham J B. On kinematic waves I：Flow movement in long rivers. Proceedings of the Royal Society A，1955，229：281-316.

［4］Lighthill M J，Whitham J B. On kinematic waves II： A theory of traffic flow in long crowded roads［R］. Proceedings of the Royal Society A，1955，229：317-345.

［5］王殿海.交通流理论［M］.北京：人民交通出版社，2002.

［6］Helbing D Tilch B. Generalized model of traffic congestion and numerical simulation［R］. Physics Research，1998，1644：37-46.

［7］徐周华，牟军敏，季永清.内河水域船舶领域三维模型的研究［J］.武汉理工大学学报，2004，28（3）：380-383.

［8］Daganzo C F Requiem for second order fluid approximations of traffic flow［R］. Transportation Research Part B，1995，29：277-286.

［9］董宇，姜晔，何良德.内河航道通过能力计算方法研究［J］.港口和航道工程，2007（1）：60-65.

Study on Vessel Traffic Flow Dynamic Model of Inland Waterways

Bao Yehui1， Yang Haifei2
（1. JSTI Group， Nanjing 210017， China； 2. Hohai University， Nanjing 210098， China）

By analyzing the derivation process of the traditional car-following model， it is found that the simplification form of the traditional following model can not completely describe the complicated vessel traffic conditions such as vessel dimension distribution， difference of power performance， water resistance and so on. To conquer the previous limitation， viscous term is added to build a vessel-following model. By turning the microcosmic parameters in this following model to macroscopic parameters， a vessel traffic flow dynamic model is established， and the numerical simulation indicates that the proposed model can reproduce a large number of the real vessel traffic phenomena.

vessel traffic flow； dynamic model； inland waterway； digital simulation； viscous resistance

U611

A

1672-9889（2016）01-0084-03

鲍业辉（1984-），女，山东济宁人，工程师，主要从事交通规划、水运工程设计等工作。

2015-05-27）