基于空间网格法的某地道箱体设计与计算
2016-08-04张建军宿霄男
张建军,宿霄男,杨 阳
(中国市政工程华北设计研究总院有限公司,天津 300074)
基于空间网格法的某地道箱体设计与计算
张建军,宿霄男,杨 阳
(中国市政工程华北设计研究总院有限公司,天津 300074)
以呼和浩特市万通路(东客站西路)地下通道及管网为工程背景,采用“空间网格法”对地道箱体进行网格划分,利用Midas Civil有限元软件建立地道箱体结构的空间网格有限元模型,并通过Ansys中的20节点实体单元(solid186单元)验证空间网格有限元模型的刚度、应力以及内力模拟的正确性。之后根据工程中实际的荷载、边界条件以及施工阶段对所建立的有限元模型进行模拟、计算和配筋设计。结果表明:采用Midas Civil对地道箱体结构进行空间网格法建模具有计算速度快、刚度模拟准、便于加载和配筋设计等优点。
地下通道;地道箱体;空间网格法;有限元模型;配筋设计
随着城市交通的发展,下穿地道的建设越来越多,框架箱体是城市地道必不可少的结构形式。近些年来,许多斜交道路也采用下穿地道立交形式,斜交箱体也被广泛的采用。箱体结构计算的历史并不长久,1975年日本的渡道健、手冢民之佑等人[1]才第一次将箱形框架结构作为一种建筑结构形式。20世纪80年代,国内学者编写的《倒虹吸管》、《涵洞》是国内较早的有关箱体结构设计方面的专著,但这些专著中仅对对称结构下单一对称荷载工况下的箱体结构进行了计算与设计[2],这是远远不够的。对于荷载不均匀、结构不对称且斜交的箱体来说,如按照以往正交箱体配筋方式对斜交箱体进行配筋,则将会造成局部的浪费或不足[3]。
现在桥涵结构计算常用的有限元分析与设计软件,如桥梁博士、Midas Civil等,都是主要围绕梁单元进行的,其中Midas Civil虽然能进行板、实体等单元的分析,但功能较为有限,且该软件针对桥涵结构的移动荷载分析以及配筋设计的模块也都只能适用于板单元或梁单元。因此,如何将空间的地道箱体结构转换成梁、板单元以供Midas Civil进行计算与设计成为了迫切需要解决的技术问题。
本文结合呼和浩特市万通路(东客站西路)地下通道及管网工程,采用空间网格法对实际地道箱体进行模拟、计算与设计,旨在解决在荷载不均匀分布以及箱体斜交情况下的计算与设计等问题,也使得采用Midas Civil对地道箱体进行精确地配筋设计成为可能。
1 空间网格模型的建立格式
空间网格法是一种广泛应用与各项领域的实用方法。在桥梁的计算与设计中,这是一种比梁格法[4]更加精细的方法,主要应用于箱梁[5-6]的计算与设计中,但很少应用于地道箱体中。为了在地道箱体的计算与设计之中应用空间网格法,本文首先将地道箱体结构分离成顶板、腹板和底板等几个部分,如图1所示。然后将每一块板根据梁格法的原理转换为一张由空间梁单元组成的“网”。地道箱体结构由多少个板组成,也就可以由多少个这样的空间网组成,这些“网”空间交织在一起,形成了“空间网格”,如图2所示[7]。
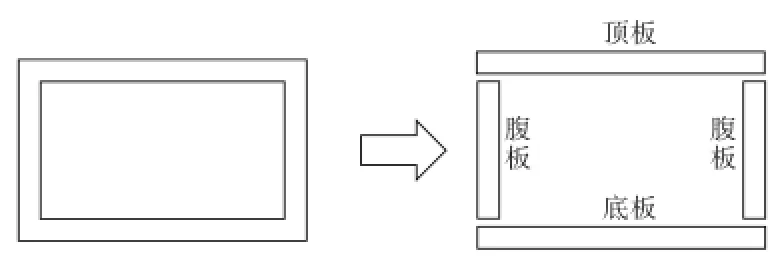
图1 由“板”表达的箱形结构

图2 由空间网格表达的箱形结构
通过该方法得到的有限元模型在合理的网格划分以及截面、材料选择的前提下,能够较好地表现出地道箱体结构的完整受力特征,如局部效应、弯矩不均匀分布效应等,为箱体的精确配筋设计提供依据。
下文对于呼和浩特市万通路(东客站西路)地下通道及管网工程中如图3所示的地道箱体结构,采用Midas Civil进行空间网格法建模,网格单位宽度取1 m,具体步骤如下:

图3 地道箱体计算模型示意图
(1)将箱形结构划分成若干个如图4所示的梁单元单位宽度(以下简称“单宽”)框架,结构最外侧2个框架宽度取一半的单宽并设置左(右)偏心,以便于后续面荷载的施加。梁高取值与各板的厚度相同,截面形式如图5所示,材料为C30混凝土。
(2)为了更好地模拟底部边界条件,底板单宽梁截面采用中下偏心,并用弹性连接中的刚性连接将腹板底与底板对应节点相连。
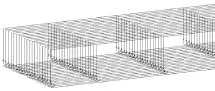
图4 单宽梁框架模拟示意图

图5 各网格梁单元截面形式
(3)将各单宽梁框架划分成与单位宽度相近长度的梁单元,称之为纵梁,如图6所示(图中每2个节点之间为1个纵梁单元)。
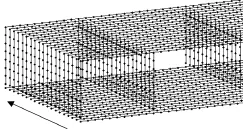
图6 单元划分示意图
(4)在单宽框架的对应各梁单元节点间,沿箱室纵向(图6中箭头所示方向)用可以代表节点左右两侧各一半纵向弯曲刚度的梁单元相连,称之为横梁。截面高度与各板厚相同,宽度等于节点两侧纵梁单元长度和的一半(左右纵梁单元长度不等的横梁需设置截面偏心),材料的选用和纵梁相同,但不计容重,连接后组成空间网格,如图7所示。

图7 空间网格示意图
通过上面4步,就可以得到任意箱体的空间网格模型。
为了验证该模型的刚度模拟正确性,将模型底部节点全部固结,计算自重作用下的变形及内力,并与较为精确的Ansys中20节点2次6面体实体单元——solid186单元模型(网格精度0.5m)的计算结果进行比较。2种模型的位移等值示意图如图8所示,计算结果如表1所示。
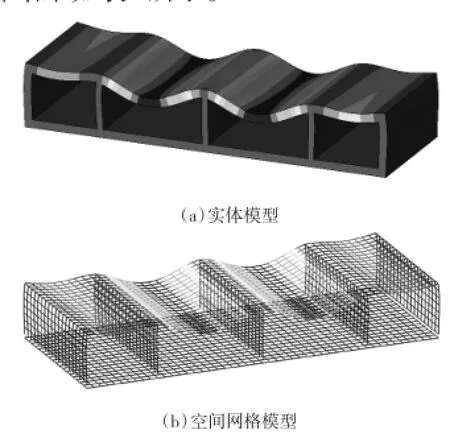
图8 实体单元模型与空间网格模型自重作用下的位移等值图
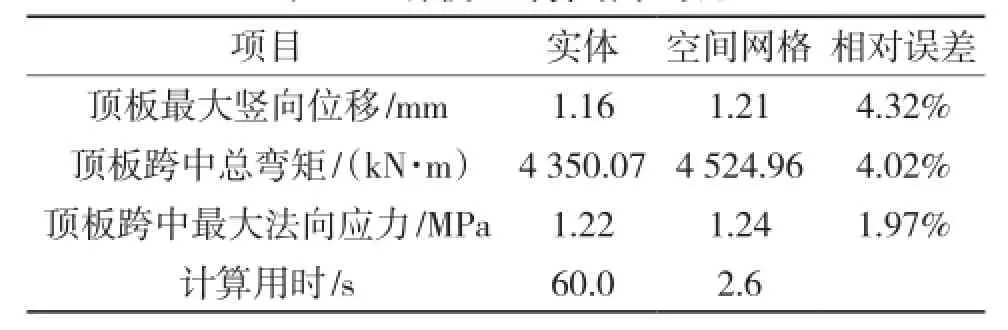
表1 2种模型计算结果对比
通过上表的对比可得,空间网格法地道箱体模型在刚度、内力以及应力计算结果方面均大于较为精确的实体单元模型的计算结果,且相对误差均小于5%,可以满足工程上对计算精度的要求,计算用时较短。
2 地道箱体的计算与配筋设计流程
将针对上面的模型结合桥梁中常用的设计软件Midas Civil对实际工程中的结构进行细致的模拟、计算以及配筋设计。
2.1 边界条件的模拟
地道箱体结构通常是完全埋藏在土中的结构,应考虑两侧以及底面土对结构的约束作用。
2.1.1 底部边界模拟
根据工程地址勘测资料,该箱体底部全部位于中密砾砂层,采用m法,查《公路桥涵地基与基础设计规范》(JTG D63—2007)中表P.0.2-1可得,砾砂的m值和m0值取30 000 kN/m4。则地基竖向抗力系数C0=m0×h,当h<10 m时,取C0=10×m0,一般的地道箱体结构地面埋深均小于10 m,故本例地基竖向抗力系数C0=30 000 kN/m3。
由于土壤对结构的约束只能提供法向推力而不能提供拉力,因此先在结构底面建立容重为0且厚度极小的辅助板单元,并在其上施加只受压的“边界-面弹簧”,数值则为前面的C0。对于底部土体,除了对结构提供法向约束外,还有沿垂直法向各个方向的侧向摩阻约束,这种约束相比法向约束要小的多,大约在1个数量级以上,工程上通常取5%的法向约束作为底面土体的侧向约束,类型则选择面弹簧的“线性”,同样施加在结构底面的辅助板单元上。
2.1.2 侧土约束模拟
这里同样是采用m法,非岩石地基深度z处的地基水平向抗力系数Cz=m×z,对于明挖法的箱体,侧面主要是压实填土,则根据填土的类型选择对应的m值,并对不同深度的位置施加不同的只受压节点弹性支撑即可。
2.2 荷载的施加
该地道箱体的荷载根据《公路桥涵设计通用规范》(JTG D60—2004)(以下简称《桥通规》),主要考虑永久作用与可变作用。
2.2.1 永久作用
永久作用主要包含自重以及铺装和填土的压力。其中需注意自重系数为-1.04,用以将软件中素混凝土的容重修改为钢筋混凝土的容重。在施加压力荷载时,要注意先在空间网格模型上覆盖一层辅助板单元,之后再根据实际情况施加均布压力荷载或自定义面荷载。
顶板覆土的竖向压力宜根据《桥通规》中第2.4.3条第6款的规定,按压实填土重力的竖向压力强度标准值qv=γh计算,其中γ为土的容重,h为填土厚度。侧土压力则宜根据《道路隧道设计规范》(DG-TJ08-2033—2008)(上海)中第8.2.2条第5款规定,使用阶段水平地层压力应按静止土压力计算。
2.2.2 可变作用
可变作用主要包括温度荷载、结构内外的车道(车辆)和人群荷载以及车辆荷载对结构侧面产生的等效土压力几部分组成。
对于不长的地道箱体(一般为几米到一二十米),由于其和外界空气相通,应考虑结构在整体升温情况下,受四周土体约束所产生的效应;对于多节的长大隧道,则应在洞口处考虑这种效应,中间的箱体考虑这种效应时应进行相应的折减。
对于箱体受到的移动荷载,则应考虑顶板车道荷载、顶板车辆荷载、顶板人群及非机动车荷载、底板车道荷载、底板人群及非机动车荷载以及箱体两侧土体顶面车辆荷载对箱体侧壁产生的等效活荷载几种情况。其中前四种情况可以直接采用辅助板单元影响面加载法(即车道面)加载,但最后一种情况应从结构底面与结构侧面成45°-φ/2角度延伸至顶面所形成的三角形顶边的长度作为车辆荷载的加载范围,如图9中l0所示。
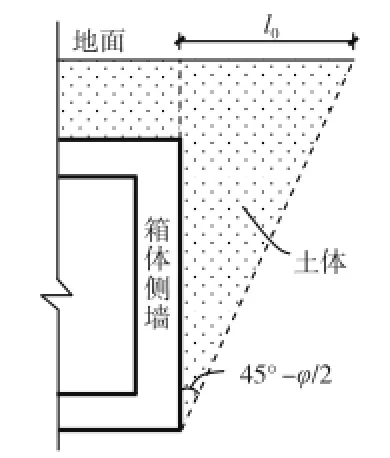
图9 车辆荷载加载范围
2.3 施工阶段的模拟以及荷载组合
对于分阶段浇筑的混凝土结构,应根据实际可能的施工流程对有限元模拟进行施工阶段划分,并考虑混凝土的收缩和徐变这个重要特性。
在Midas Civil中可以通过定义时间依存材料、将时间依存性与材料进行连接以及修改单元依存材料特性3个步骤对混凝土结构的收缩和徐变进行定义。之后根据实际施工流程以及结构受力的最不利原则拟定如下施工方案,如表2所示。

表2 施工阶段划分
进行完施工阶段的划分即可运行结构计算,运行完结构计算可得到结构在不同荷载工况下的单项内力以及不同施工阶段下的施工阶段结构内力。对这些内力参照《桥通规》中第4.1.6条以及4.1.7条进行作用效应组合,即可得到计算模型的各单宽梁单元的在各种荷载组合下的内力包络图,即各单宽梁单元的最不利内力。本文以结构建成10年时的承载能力极限状态弯矩为例,简要示意该结构的受力情况,如图10所示。

图10 承载能力极限状态弯矩包络图
2.4 配筋设计与验算
根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)中有关混凝土构件的规定进行配筋设计与验算。
在Midas Civil中,软件提供了RC(混凝土结构)设计与验算功能,该功能不仅与上面的现行规范结合紧密,而且还能针对地道箱体空间网格法模型中的单位宽度梁单元进行批量验算,大大提高了工作效率。具体操作流程如下:(1)设置RC设计参数/材料;(2)对需要进行RC设计的截面输入钢筋;(3)为了提高计算效率,选择需要进行RC设计的关键截面进行设计与验算;(4)输入裂缝宽度系数;(5)运行RC设计。
通过上面的操作,即可获知关键设计截面的各项内力、应力以及裂缝等是否满足现行规范的要求,如不满足规范,对结构尺寸或钢筋布置形式进行修改后重新运行RC设计即可再次验算。表3为结构建成10年时单位宽度截面的承载能力极限状态弯矩的验算结果。
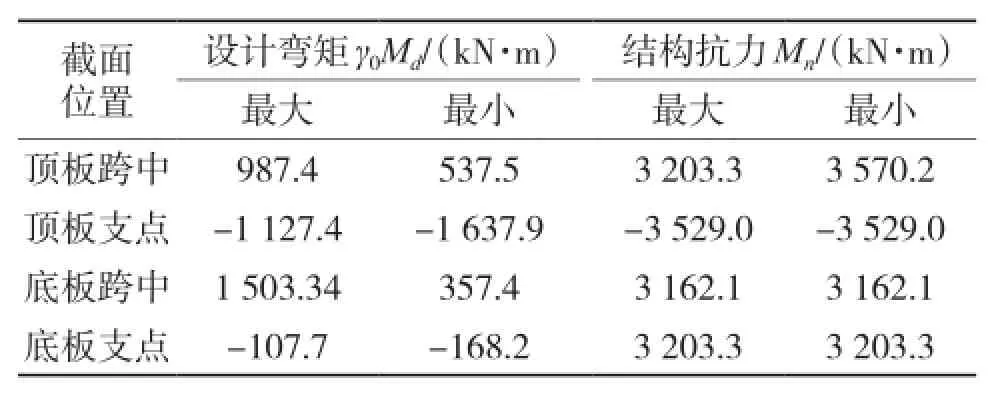
表3 承载能力极限状态最不利弯矩验算表
3 结语
基于“空间网格法”模型并结合midas Civil软件对地道箱体结构进行模拟、计算以及设计具有如下几个优点:(1)计算速度相对实体单元模型较快;(2)刚度模拟较为准确;(3)可模拟斜交箱体并考虑恒荷载的不均匀分布,为结构精细化配筋提供方便,适用性强;(4)移动荷载可根据辅助板单元的影响面自动最不利加载,且无需考虑横向分布;(5)计算结果以内力形式输出,与桥梁常用的半概率极限状态控制法的要求相符;(6)内力计算结果略微偏大(不超过5%),在精细的前提下提高了结构的安全储备;(7)以1 m为单位宽度建立空间网格模型,方便与软件结合进行配筋设计。
综上,采用本文第3部分所介绍的方法对实际工程中的地道箱体结构进行建模计算与设计是可行的。
[1]张猛玫.箱形涵洞结构设计及其CAD系统的研究与实现[D].北京:北京航空航天大学,2004.
[2]李武群.考虑剪切变形的带刚性域箱涵结构分析与程序设计[D].天津:天津大学,2008.
[3]禹国辉,朱尔玉,李学民.斜交地道箱体结构在钝角处的受力和配筋特点[J].北京交通大学学报,2013,37(1):124-127,133.
[4]Edmund C Hambly. Bridge Deck Behaviour[M]. London,1976.
[5]徐栋,徐方圆,赵瑜,等.箱梁结构完整验算应力和空间网格模型[J].土木工程学报,2014,47(5):46-55.
[6] 徐栋,赵瑜,刘超.混凝土桥梁结构使用精细化分析与配筋设计[M].北京:人民交通出版社,2013.
[7]徐栋,刘超,赵瑜. 混凝土桥梁结构分析与配筋设计的精细化[C]∥第十九届全国桥梁学术会议文集(下册).2010.
Calculation and Design of a Underpass Box Based on Spatial Grid Method
Zhang Jianjun, Su Xiaonan, Yang Yang
(North China Municipal Engineering Design & Research Institute Co., Ltd., Tianjin 300074, China)
Taking Hohhot Wantong road (also named East Railway Station West Road) underground tunnel and pipe network engineering as background, the spatial grid finite element model of tunnel box structure is built by finite element software Midas Civil. The simulation accuracy of the stiffness, stress and internal force are verified by 20-node solid element model built by Ansys. Then the simulation, computation and reinforcement design are conducted according to the real load, boundary condition and construction stage basen on the model. Finally, some advantages of Midas Civil model for tunnel box by spatial grid method are concluded, such as the high computing speed, accurary stiffness simulation, easy to load, easy to reinforcement design and so on. Key words: underpass; underpass box; spatial grid method; finite element model; reinforcement design
U449.1
A
1672-9889(2016)01-0071-05
张建军(1978-),男,内蒙古人,高级工程师,主要从事道路、桥梁、隧道方面的工作。
2015-06-16)
