有限元插值技术在振动法测量索力中的应用

李　欣，邓凌宇，宋一凡

（长安大学 公路学院，陕西 西安 710064）

有限元插值技术在振动法测量索力中的应用

李欣，邓凌宇，宋一凡

（长安大学 公路学院，陕西 西安 710064）

文章分析了弦理论在索力测量中的误差，以动力分析有限元原理为基础，借助Ansys建立了拉索自由振动的模型；利用三次样条插值法获得了频率与索力的对应关系，并通过工程实例验证了插值方法的可靠性与准确性。

索力测量；振动法；弦理论；自振频率；样条插值

斜拉桥斜拉索的受力情况对其施工阶段的施工控制与运营阶段的健康性评价均具有重要意义。目前斜拉桥索力测量的方法有4种：千斤顶油表法、压力传感器法、振动频率法［1］和磁通量法。千斤顶油表法只能在施工阶段张拉索时使用；穿心式压力传感器造价昂贵，不适合大规模使用；磁通量法是一种新的测试方法，在国内的使用还不是特别广泛。本文将介绍动力分析有限元原理和三次样条插值求解索力的方法，该方法考虑了抗弯刚度或垂度，且不受边界条件的限制，适用范围较广。

1 常用的斜拉桥索力测量方法

1.1 振动频率法

振动频率法是国内斜拉桥索力测量使用最为广泛的方法，常用的测试原理是张弦理论，计算公式如下［2-3］：

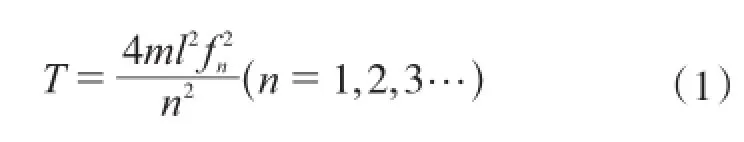
式中：T为索的拉力，m为索的线密度；l为索长；fn为索的自由振动频率。

张弦理论认为斜拉索像一根张紧的弦，没有抗弯刚度与垂度，而研究表明，忽略斜拉索的抗弯刚度和垂度在一些情况下会产生较大的误差［4-6］。

1.2 动力分析有限元法

将连续体斜拉索离散为具有多个集中质量的多自由度体系，利用d'Alembert 原理直接考虑作用于质量上全部力的平衡可建立一般情况下的运动方程。沿自由度方向作用的荷载用向量p（t）表示，由运动引起的3个抗力惯性力、阻尼力和弹性力可分别表示为向量fI（t）、fD（t）和fS（t）。这些力的平衡方程为：

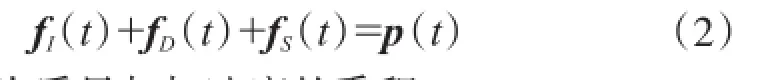
惯性力为质量与加速度的乘积：

根据粘滞阻尼机理，阻尼力为阻尼常数C和速度v˙的乘积：

弹性力以及由轴向力引起的位移方向的附加荷载之和为刚度K与位移v的乘积：

该刚度矩阵反映了索力对位移的影响。

把式（3）、（4）、（5）带入式（2），就可以得到一般情况下体系的运动方程：

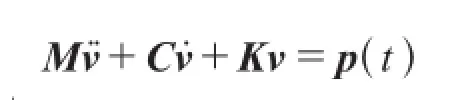
略去阻尼矩阵和荷载向量可得到无阻尼自由振动情况下体系的运动方程：

其中0为零向量，假设多自由度体系的振动为简谐运动，则位移可表达为：

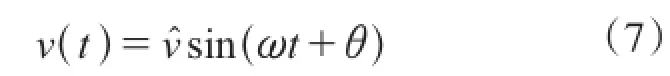
式中：v^为振幅；θ为相位角；ω为体系频率。

对式（7）取二次导数，得到自由振动的加速度：

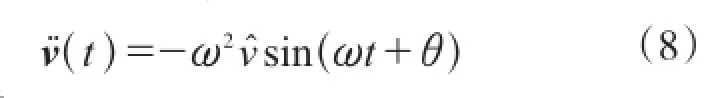
将式（7）与式（8）带入式（6），则有：

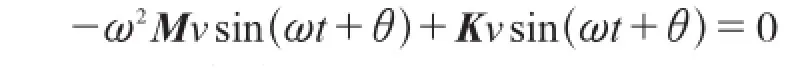
正弦项是任意的，因此可导出：

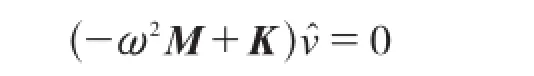
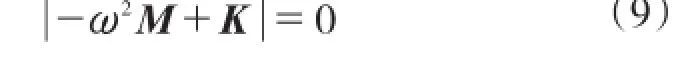
时，该方程组才有非零解。

方程（9）即体系的频率方程。设体系的自由度为n，则展开行列式得到一个频率参数为ω2的n次方程，其解可表示为：

由Cramer法则知，只有当系数行列式为0，即

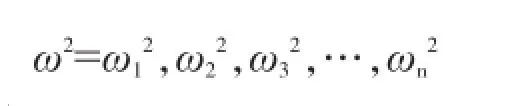
每一个解对应着一个可能出现的振型。频率的变化反映了索力的变化。相对与动力体系静力平衡位置的运动方程不受重力影响，实际索力可由不考虑重力的动力分析结果与在重力作用下的静力分析结果相加获得［7］。

2 斜拉桥的数学建模

2.1 考虑垂度的情况

在考虑垂度的情况下，斜拉桥的斜拉建模主要有3种方法［8］：等效弹性模量法、多段直杆法和曲线索单元法。本文采用多段直杆法建立斜拉索的动力模型。多段直杆法关于索的基本假设如下：

（1）索是理想柔性的，不能承压，不能承受弯矩；

（2）索的受拉符合胡克定律。

多段直杆法将斜拉索等效为一系列铰接的无质量链杆，在自重作用下这一系列铰接的链杆会呈现悬链线形状，从而达到对斜拉索垂度的模拟。索的自重和其它荷载集中作用在链杆的节点上，几何非线性分析能够保证节点满足平衡和协调的条件。无限数量的链杆能精确模拟斜拉索的自然状态，对于垂度较大的悬索桥主缆，通常小数量的链杆就能给出满意的结果，对于垂度不大的斜拉桥斜拉索，所需链杆的数量就更少了。

2.2 考虑刚度的情况

对于上承式和中承式拱桥的吊杆与斜拉桥近桥塔处的短索，基本可以忽略垂度的影响，抗弯刚度的影响却不能忽略，此时应将其看作一根轴向受拉的欧拉-伯努利梁。梁的截面形式简化为圆形，面积与实际索截面面积相同。采用梁理论分析时，有一个问题需要指出：欧拉-伯努力梁认为梁受弯时截面是平面，即认为索是一根钢棒，而现实中的平行钢丝索是由许多根钢丝组成，由这些钢丝组成的截面并不是一个密不可分的整体；钢丝与钢丝之间存在摩擦力，某一根钢丝的变形会影响其它钢丝的变形，钢丝截面的变形并不独立，全截面惯性矩也不等于单根钢丝的惯性矩乘以钢丝数。

2.3 采用降温法调整索力

超静定结构在温度作用下会产生应力。在梁端固结时，梁的截面面积A、弹性模量E和线膨胀系数α均是常数。忽略梁的横向变形，则梁的轴向应力可以用胡克定律求得：

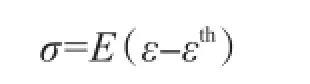
式中：ε为总应变；εth为温度应变，εth=αΔθ，Δθ为温度变化量。

因为单元梁端固结，故ε=0，因此单元轴向应力可表达为：

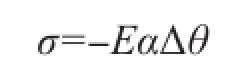
轴向力可表达为：

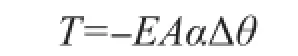
需要模拟索的张拉时，可设定初始温度为0 ℃，将设计索力代入轴向力表达式，然后在设计索力对应的温度上下以一定的温度差取几个温度，形成一个温度序列，温度的不同造成了索力的不同，从而实现对索力的调整。如果材料的实际线膨胀系数过小，导致降温过大，可将实际的线膨胀系数放大若干倍，即赋予材料虚拟的线膨胀系数。材料线膨胀系数的改变不会影响结构频率，故可采用此法。

2.4 Ansys建模

（1）建立块，即建立几何模型。

（2）赋予所建块以材料属性。本文只需输入钢材的密度、弹性模量、线膨胀系数和截面参数。

（3）建立分析步。施加荷载与边界条件的步骤类型为常规选项下的静力分析，提取结构频率的步骤类型为线性扰动选项下的频率。

（4）施加荷载与边界条件。本文考虑的荷载只有重力场，边界条件为固结。实际中索的边界条件介于铰接与固结之间，更接近于固结。在利用多段直杆法建模时，需首先将所有节点均作固结处理，在降温结束后再释放非支点节点的自由度。

（5）划分网格。

（6）提交工作。

（7）查看结果。在结果文件的特征值输出中，可以读取结构的各阶频率。

3 利用3次样条插值法求索力

样条插值是采用低阶分段多项式插值的形式，因其避免了龙格现象且能得到光滑曲线，故在工程设计中得到广泛的应用。 本文采用三次样条插值法，并使用origin软件辅助计算。

在设计索力上下一定范围内取n个索力值，利用轴向力与温度的表达式计算出n个温度，在有限元软件Ansys中建立考虑重力影响的斜拉索自由振动的模型，读取频率以及各频率对应的索力，这样就得到了n组频率与索力的数值，这n组频率与索力数值就构成了插值的基础数据。在实际测量中获得真实的斜拉索自振频率后，借助上述n组数据，利用origin软件绘出索力与频率的三次样条曲线，通过图像可求得实测频率对应的索力，也可利用cubic spline功能直接得到实测频率在三次样条插值中对应的索力。

4 工程实例分析

迎客大桥位于广东省河源市南部，跨径组合为40.5 m+76.5 m+145 m，是一座双幅独塔四索面预应力混凝土斜拉桥。拉索为平行钢丝索，采用HDPE护套防护，单幅共68根拉索，索长33.2～154.2 m。

4.1 3种方法测量索力的结果

以迎客大桥斜拉索为研究对象，选取左幅3根拉索，使用JMM—268动测仪拾取拉索自由振动主振频率，分别根据弦理论、穿心式压力传感器读数与本文方法求其塔端索力，并认为穿心式压力传感器读数最为接近塔端索力真实值。拉索参数见表1，本文所述样条拟合曲线见图1，索力计算结果见表2。

4.2 结果分析

（1）本文所选三根索均较短，以梁来考虑更为合理，由表2知，本文方法梁模型的计算值与穿心式压力传感器的读数最为接近，显示了本文方法的可靠性。本文方法梁模型计算的3根索的索力值均略大于穿心式压力传感器读数，可能是抗弯刚度取值误差所致，因为索的HDPE保护套也会增加索的刚度。

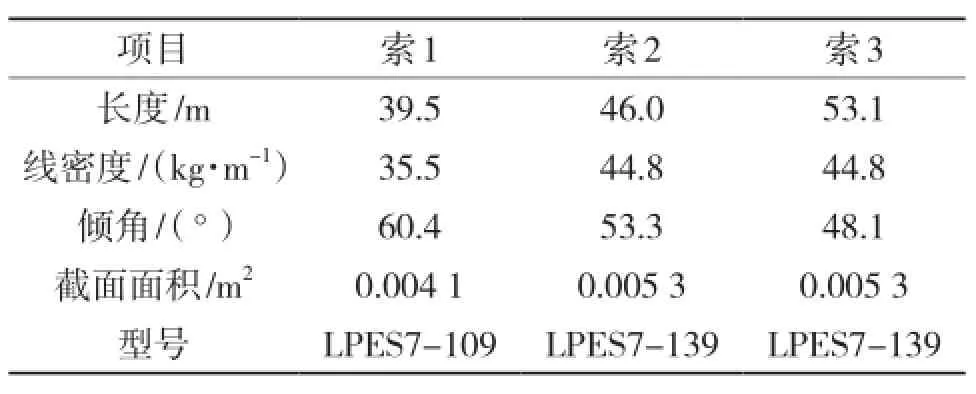
表1 斜拉索的参数

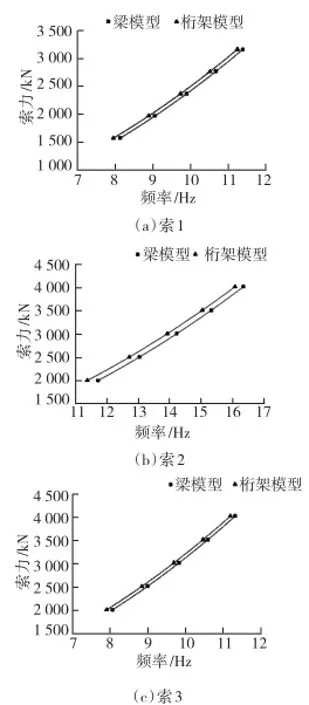
图1 本文方法的拟合曲线

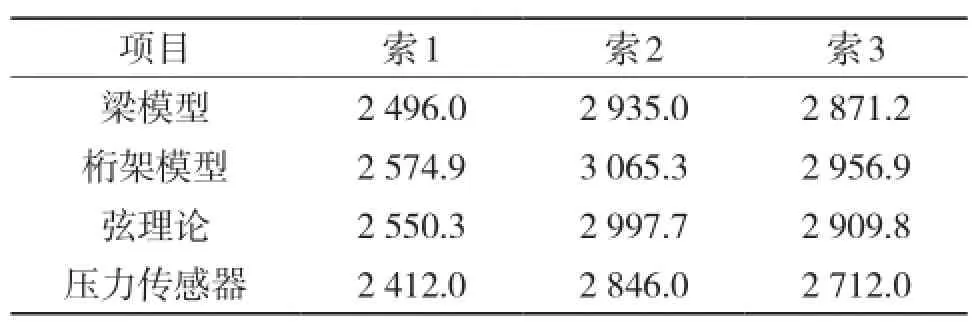
表2 索力计算结果 kN

（2）由表2知，本文方法桁架模型的计算值与弦理论计算值很接近，这个结果与误差的定性分析相符，显示了本文方法的可靠性。桁架模型是忽略抗弯刚度考虑垂度的模型，本文拉索较短，垂度不大，故桁架模型非常接近弦理论既不考虑抗弯刚度也不考虑垂度的假设，且桁架模型考虑了重力影响，索力值略大与弦理论计算值是合理的。

5 结语

大多数索力仪依据的张弦理论忽略了拉索固有的刚度与垂度且视索的边界条件为铰接，这些过分理想的假设对索力测量的精度造成了影响。本文通过有限元法与三次样条插值法成功描述了频率与索力的对应关系，并用实例检验了该法的合理性和可靠性。该法可考虑垂度与刚度及许多解析法难以考虑的因素，并且不受边界条件的限制，具有较大的适用范围与工程实用价值，但其建模过程较为繁琐是一个弊端。

［1］ 林元培.斜拉桥［M］.北京：人民交通出版社，2001.

［2］Humar J L. Dynamics of Structures. Prentice-Hall. Inc.， Englewood Cliffs，N.J.，1990.

［3］ 吴康雄，刘克明，杨金喜.基于频率法的索力测量系统.中国公路学报［J］.2006，19（2）：62-66.

［4］Starossek U. Cable dynamics-a review［J］. Structural Engineering International，1993，3（2）：172-175.

［5］Zui H，Shinke T，Namita Y. Practical Formulas for Estimation of Cable tension by Vibration Method［J］. Jounal of Structral Engineering ASCE，1996，122（6）：652-655.

［6］宋一凡，贺拴海，吴小平.固端刚性拉索索力分析能量法［J］.西安公路交通大学学报，2001（1）：55-56.

［7］彭津J，克拉夫R.结构动力学（第二版）［M］.北京：高等教育出版社，2007.

［8］ 张晓壳，陈宁，王应良，等.斜拉桥的数学建模［J］.国外桥梁，1998（2）：52-53.

Application of Finite Element Interpolation Technology in Cable Force Measurement Based on Frequency Method

Li Xin， Deng Lingyu， Song Yifan
（School of Highway， Chang'an University， Xi'an 710064， China）

This paper analyzes the errors of taut string theory in cable force measurement. Based on the finite methods of dynamic analysis， cable models of free vibration are built using Ansys and the relation between natural frequency and cable tension is obtained according to cubic spline interpolation. The reliability and precision of the method are verified by engineering practice. Key words: cable force measurement； vibration method； string theory； natural frequency of vibration； spline interpolation

U448.27

A

1672-9889（2016）01-0048-03

李欣（1990-），男，陕西榆林人，硕士研究生，研究方向桥梁结构设计。

2015-05-04）