小波-ICA联合技术在水工结构应变损伤识别中的应用

张建伟， 暴振磊， 江　琦

(华北水利水电大学 水利学院，郑州　450045)

小波-ICA联合技术在水工结构应变损伤识别中的应用

张建伟， 暴振磊， 江琦

(华北水利水电大学 水利学院，郑州450045)

针对环境激励下的结构参数辨识问题，提出一种小波阈值和独立分量分析(Independent Component Analysis, ICA)联合辨识水流激励下水工结构模态参数的方法。利用小波阈值对原始信号进行降噪处理，减小环境激励对各响应分量间独立性的干扰，使其满足ICA的分离假定；然后运用ICA辨识结构模态参数，通过不同工况下应变模态参数的对比，实现对水工结构损伤的识别。运用该方法对水流激励下的悬臂梁模型试验进行分析研究，结果表明，联合运用小波阈值和ICA可有效辨识水工结构的模态参数，利用应变模态参数的差异可识别结构是否存在损伤。该方法为大型水工结构在水流激励下的结构模态参数辨识提供捷径，为结构的安全运行与在线监测提供参考，应用前景广阔。

环境激励；水工结构；小波分析；独立分量分析；损伤识别

模态作为结构的固有振动特性，能够准确预报某频段内结构在外部或内部各种振源作用下的实际振动响应，工作模态参数是结构运行状况的动态外在表现，通过准确的辨识模态参数可以实现水工结构无损在线动态监测，达到识别结构损伤的效果。传统的模态分析方法建立在系统输入、输出数据均为已知的基础上，利用完整的激励和响应信息进行参数辨识。然而实际工程中水工结构实际尺寸的限制、人工激励成本的高昂及其对结构运行的影响，使得结构完整输入激励信息难以准确获得，导致传统方法在实际工程中的应用受到限制，因此，仅利用响应数据的工作模态分析技术逐渐发展起来[1]。

工作模态参数辨识方法主要分为频域辨识法和时域辨识法。频域辨识法将时域内测得的数据通过傅里叶变换(简称FT)转换到频域内，而后由功率谱函数进行辨识。该类方法概念清晰，不易遗漏模态。时域辨识法直接应用实测响应数据在时域内进行参数辨识，避免了频域辨识法中由于傅里叶变换而引起的截断误差，由此提高了辨识精度[2]。近年来随着计算机技术、信号分析技术和试验手段的进步，基于振动的模态参数辨识研究得到了长足进展，研究对象已从单一较小线性不变结构向大型多相耦合非线性动力时变体系过渡，激励方式由简单的脉冲方式发展到复杂的环境随机激励，研究结构所处的背景环境由无干扰噪声到强干扰、强耦合、多特征条件下的随机噪声，研究方法从经典的频域方法发展到现代时-频联合分析方法和人工智能方法[3]。其中，作为一种经典的盲源分离技术的独立分量分析受到的关注最多。ICA是在源信号未知的情况下，假设信号相互独立，从多维数据中寻找具有统计独立和非高斯的成分，进而分离出独立的源信号分量。由于其操作方便、计算快速、分解结果优于传统的信号分析技术，ICA在参数识别领域已取得一定的成果，但在实际结构参数识别应用中仍存在一些局限性。Kerschen利用ICA成功进行时域下阻尼限制在1%以下的结构系统参数识别[4]；McNail利用改进的Hebbian-like算法将ICA扩展至高阻尼结构的自由响应参数识别，但环境激励下的结构参数识别问题并未得到很好的解决[5]。

基于上述研究，提出一种适用于环境激励下水工结构的工作模态参数识别方法，该方法通过小波阈值对泄流振动数据进行预处理，提取结构振动有效信息，降低环境噪声对ICA的影响；然后利用ICA辨识结构的工作模态参数，通过对比不同工况下的模态参数，最终达到损伤识别的目的。

1基本原理

1.1小波阈值降噪

小波阈值降噪是利用变换阈值对含噪声信号进行小波阈值处理，从而除去或减少噪声的影响，然后对处理后的系数进行小波重构得到较好的真实信号的估计[6]。其基本原理是小波分解后白噪声仍然是白噪声，分布广泛，但其幅值较小；而有用信号则被压缩到少量小波系数中，其幅值大。根据这一性质，设计门限值，认为小于此门限值的小波系数是噪声小波系数，应全部置零，大于此门限值的小波系数为有用信号，应保留，从而除去或减少噪声的影响。经处理后的系数通过小波重构得到较好的真实信号的估计。Donoho提出两种阈值处理方法[6]：

1) 硬阈值函数：

(1)

2) 软阈值函数：

Donoho给出了阈值求解公式：

(3)

式中：σ表示噪声方差，N表示信号数据长度。

1.2独立分量分析(ICA)

独立分量分析(ICA)是20世纪90年代后期发展起来的一种统计数据分析和信号处理方法，是一种经典的盲源分离技术。其工作原理是：在源信号未知的情况下，假设信号相互独立，从多维数据中寻找具有统计独立和非高斯的成分，进而分离出独立的源信号分量，实现对多信号重叠情况的分解提取工作。由于其操作方便、计算快速、分解结果优于传统的信号分析技术，独立分量分析在通信工程、神经科学、图像处理等[7]多个领域得到广泛应用。

1.2.1ICA的问题描述

假定n维源信号矢量s(t)=[s1(t),s2(t),…,sn(t)]T和m维观测矢量x(t)=[x1(t),x2(t),…,xm(t)]T满足：

x(t)=As(t)

(4)

式中：A∈Rm×n是未知的混叠矩阵。

为了最大限度得到源信号的最优估计，需找到合适的分离矩阵W，通过分离矩阵将各独立信号从混合信号中提取分离，即：

y(t)=Wx(t)

(5)

式中：y(t)=[y1(t),y2(t),…,yn(t)]T为源信号矢量s(t)的估计。当W和A互为逆矩阵时，即WA=E(E为单位矩阵)时，ICA分离结束。

1.2.2ICA的基本假定

在源信号和系统特性均未知的情况下，如果缺少其他相关的假设条件，仅依靠观测信号很难得到ICA分离问题的期望解。为了使问题可解，对输入的源信号和混合矩阵做出以下的几点假设[8]：

(1) 混合矩阵A为非奇异矩阵(即A-1存在)；

(2) 源信号的分量个数n小于或者等于观测信号的个数m，通常假定m=n；

(3) 源信号矢量x(t)的各分量xi(t)均为零均值的平稳随机信号，且分量间满足统计独立性；

(4) 多个高斯信号的混合仍服从一个无法分离的高斯分布，所以假设源信号分量之中最多只有一个服从高斯分布。

即使对ICA做了如上基本假设，ICA分离中还是存在一些不确定性[8]，即ICA尚无法确定独立分量的顺序，得到的源信号只是对真实信号的最优估计。但这些不确定性并不影响对信号有用信息的识别，实际应用中是可以接受的。

2小波阈值降噪与ICA联合运用

2.1ICA辨识结构模态参数

N自由度系统的运动方程的物理坐标表达式为：

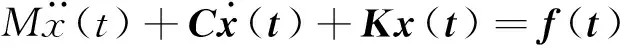
(6)

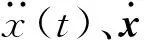
假设阻尼矩阵C为比例阻尼矩阵，即

C=αM+βK

(7)

式中：α和β为比例阻尼系数。

采用振型分解法，将物理坐标转为模态坐标，使方程解耦成为一组由模态坐标和模态参数表达的独立方程，进而求出结构相应的模态参数。系统响应按振型展开为：

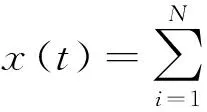
(8)

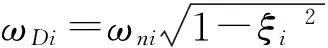
式(8)可以用矩阵形式表达为：

x(t)=Φq(t)

(9)

式中：Φ为振型矩阵，q(t)=aie-ξiωnitsin(ωDit+φi)为结构正则坐标向量。对比式(4)和(9)，正则坐标向量可以看做ICA问题中的源信号矢量，且已经满足ICA中关于源信号各分量不相关的假定条件。运用ICA分离思想，从振型分解的响应信号中估计出结构输入信号和分离矩阵W=A-1，而振型向量Φ=A=W-1。再利用傅里叶变换(FT)、希尔伯特变换(FFT)等从分离信号q(t)识别出结构的频率。因此，ICA技术可以应用于结构参数识别。

2.2小波阈值降噪与ICA联合运用

ICA局限性的主要原因在于，结构模态响应受到阻尼和环境激励的干扰，影响了各响应分量之间的独立性，响应模态的相关性逐渐增加，响应信号不再满足ICA的分离假定，进而导致ICA算法不能有效识别出结构参数[9]。因此，为精确辨识结构的振型和信号有用信息，将小波阈值降噪和ICA联合运用，对结构进行损伤识别的研究。

小波阈值降噪与ICA联合运用的步骤如下：

(1) 确定小波分解层数。信号经小波分解后白噪声能量主要分布在大多数小波空间上，在这些层次的小波空间中白噪声起控制作用，因而小波系数表现出白噪声特性；有用信号则被压缩到少数大尺度小波系数空间上数值较大的小波系数中，有用信号起主导作用，小波系数表现非白噪声特性；通过判断各层小波系数是否具有白噪声特性可以自适应地确定分解层数，即对各层小波系数进行白化检验[10]。

由数理统计知识可知，白噪声是随机函数，它由一组互不相关的随机变量构成。离散随机变量的自相关序列为：

(10)

假设离散数据序列dk(k=1,2,…,N)的自相关序列为ρ(i)(i=1,2,…,M)，若ρ(i)满足下式：

(11)

则认为dk为白噪声序列，M通常取5～10。

在实际振动测试信号中，由于白噪声中含有一种弱相关信号，无法确定是有用信号的弱相关信号还是噪声产生的随机信号，因此采用小波系数去相关的白化检验。其流程如下图1所示。

图1　小波系数去相关白化检验流程Fig.1 Flow chart for white noise detection of wavelet coefficients decorrelation

(2) 计算各层小波系数阈值。Donoho提出的阈值计算公式对于高信噪比的信号比较适用，对于被噪声淹没的低信噪比泄流结构振动信号则因保留了太多较大噪声小波系数而影响降噪效果，噪声小波系数随着分解层数的增加不断降低，且Donoho提出的阈值公式计算的是全局阈值，这显然不合理，因此采用改进阈值公式[11]：

(12)

式中：σ表示噪声方差，N表示信号数据长度，e表示底数e≈2.718 28，j表示分解层数。

(3) 选取合适的阈值函数。阈值函数通常使用Donoho提出的软、硬阈值函数。但硬阈值函数不连续，出现伪吉布斯现象，软阈值函数虽连续，但处理后的小波系数存在偏差，因此本文采用改进阈值函数：

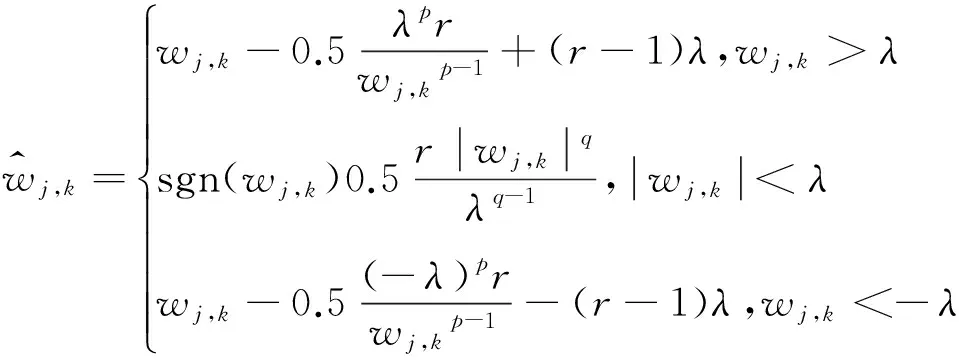
(4) 对重构信号进行ICA分解。原始信号通过小波阈值消噪后，降低了混频效应，满足ICA分解的条件，使得ICA能够正确分解信号，精确识别结构的模态参数。

(5) 对不同工况下的模态参数进行对比，实现结构的损伤识别。

3模型试验

3.1试验概况

试验以泄流激励下悬臂梁结构为研究对象，以水流作为外部环境激励源，悬臂梁底部用AB胶固结于有一定重量和厚度的钢板上，钢板与水槽底部用橡皮泥固定，以防止水流激励把模型掀翻。悬臂梁材料弹模E=155 MPa，密度ρ=2 321 kg/m3，结构尺寸6 cm×4 cm×40 cm(长×宽×高)。在其背水面和一个侧面等间距地各布置有5个应变传感器，背水面测点编号自顶部测点记为测点1，底部测点记为测点5，侧向测点编号从顶部记为测点6，侧向底部记为测点10，测点布置如图2所示。为降低试验环境中温度等因素对应变片测试结果造成影响，在同一环境中布置温度补偿片，实验时，将悬臂梁模型置于水槽中，控制上下游水位，以保证不同试验工况下能在相同流速下进行，即确保各工况下激励源能量近似相同，悬臂梁流激振动试验如图3所示，振动测试系统采用DASP智能数据采集和信号分析系统。

图2　测点布置图及温度补偿片布置图Fig.2 Survey points layout plan and temperature compensation plan

图3　悬臂梁流激振动试验Fig.3 Cantilever beam vibration test

3.2小波阈值和ICA联合辨识结构损伤

试验目的旨在设置不同的工况，通过采集泄流激励下悬臂梁的动应变响应数据，联合运用小波阈值和ICA对其进行模态参数辨识；由于应变模态相比其他模态参数对损伤有更高的敏感度[2，12]，根据应变模态的差异能够有效识别结构的局部损伤，因此，通过对比不同工况下的应变振型，进而验证本文提出的结构损伤识别方法。

试验的工况分为完好情况和损伤情况，其中损伤情况为结构在测点3迎水面处发生20 mm的损伤。应变传感器的采样频率fs=300 Hz，观测信号{xi}包含10个通道，对信号{xi}进行小波预处理，首先根据图1去相关白化检验流程确定该测点小波分解层数为5层，采用db6小波进行分解，各层阈值根据改进式(12)计算。经改进阈值函数处理后的小波系数通过小波重构得到降噪后的信号{xi′}。限于篇幅，在此仅给出损伤工况下测点2和测点3滤波前后的时程图，结果如图4和图5所示。测点2和测点3的互相关函数降噪前后对比图如图6所示。

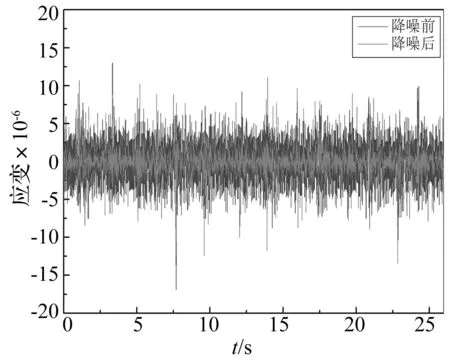
图4　测点2降噪前后时程线对比图Fig.4 Time history curve comparison of signal at point 2

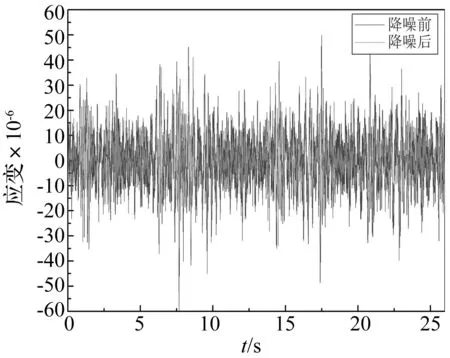
图5　测点3降噪前后时程线对比图Fig.5 Time history curve comparison of signal at point 3

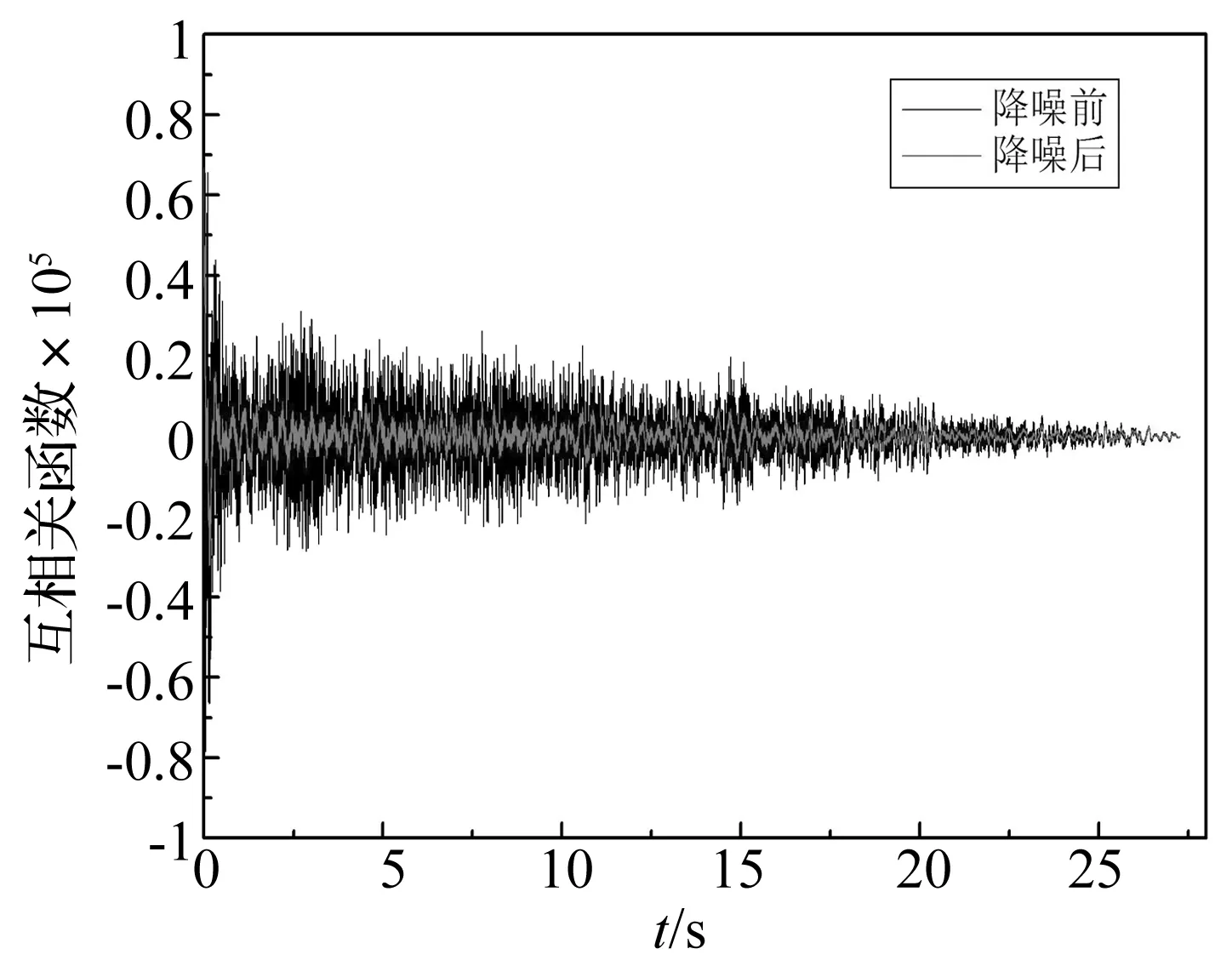
图6　测点2#、3#的互相关函数降噪前后对比图Fig.6 Cross-correlation function comparison of signal at point 2# and 3#

由图6可得：降噪后测点2和测点3的互相关函数明显减小，信号间的相关性降低，水流噪声对信号的影响大大降低，有利于ICA对结构模态参数的识别。

图7　第一阶应变振型图Fig.7 The first order strain mode

运用ICA方法分别对完好情况和损伤情况下背水面测点1#-5#降噪后的数据进行分析，得到包含模态振型信息的振型矩阵Φ和包含频率信息的分离信号q(t)；对矩阵Φ中列向量进行归一化处理，得到结构模态振型，如图7所示；从q(t)识别出不同工况下的第一阶时程图如图8所示，利用现代功率谱对图8的数据变换得到结构频谱图，如图9所示。

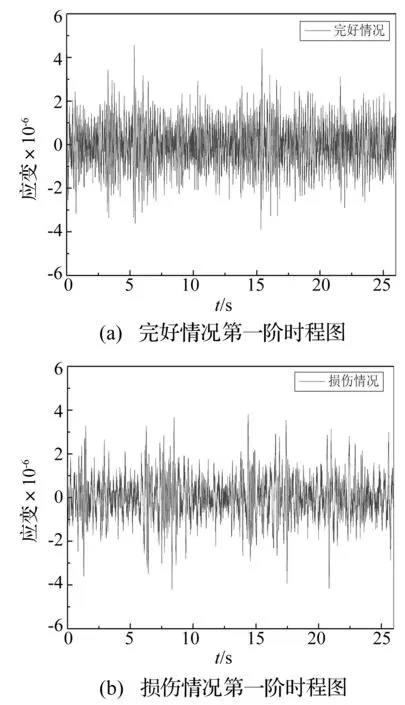
图8　第一阶时程图Fig.8 The first order time history curve

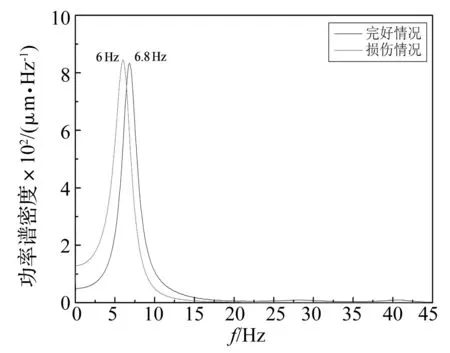
图9　第一阶频率对比图Fig.9 Power spectral density curve comparison

对比图7中完好情况和损伤情况第一阶振型图，发现测点3处发生明显的突变，说明该处有损伤发生，识别结果与本试验的工况设置吻合。另外，对比图9中两工况下的频率，发现结构发生损伤后第一阶频率由6.8 Hz变为6 Hz，表明结构发生损伤后其频率会发生相应的减小，但其对损伤的敏感度远不如应变振型。

4结论

提出一种运用小波阈值与ICA联合辨识结构振动响应模态参数，进而实现结构损伤识别的方法，该方法适用于环境激励难以测量的工程模态分析，特别是水流激励下的水工结构。应用本文方法对水流环境激励下的悬臂梁模型进行试验分析，得到如下结论：

(1) 该方法充分结合小波阈值和ICA的优点，解决了环境激励下的结构参数识别问题，特别是情况更复杂的水流激励下水工结构的参数识别问题。

(2) 根据应变模态比其他模态参数对损伤有更高敏感度的特点，对比不同工况下应变模态的差异能够识别结构的局部损伤，识别结果与设置的试验工况吻合。

(3) 将ICA引入环境激励下结构模态参数辨识领域，为大型水工结构在水流激励下结构的参数辨识提取提供了新的思路，为结构的损伤识别提供依据，具有很好的应用前景。

[ 1 ] 张建伟,李火坤,练继建，等.基于环境激励的厂房结构损伤诊断与安全评价[J].振动、测试与诊断,2012,32(4):670-674.

ZHANG Jian-wei，LI Huo-kun，LIAN Ji-jian, et al. Damage diagnosis and safety evaluation of underground powerhouse under ambient excitation[J].Journal of Vibration , Measurement & Diagnosis, 2012, 32(4): 670-674.

[ 2 ] 张建伟,张翌娜,赵瑜.泄流激励下水工结构应变模态参数时域辨识研究[J].水力发电学报,2012,31(3):199-203.

ZHANG Jian-wei, ZHANG Yi-na , ZHAO Yu. Study on strain modal parameters identification of hydraulic structure in time domain under discharge excitations[J]. Journal of Hydroelectric Engineering, 2012, 31(3):199-203.

[ 3 ] 张建伟, 康迎宾, 张翌娜,等. 基于泄流响应的高拱坝模态参数辨识与动态监测[J]. 振动与冲击, 2010, 29(9):146-150.

ZHANG Jian-wei, KANG Ying-bin, ZHANG Yi-na, et al. Modal parameter identification and dynamic monitoring of high arch dam undervibration response induced by flow discharge[J]. Journal of Vibration and Shock, 2010, 29(9):146-150.

[ 4 ] Kerschen G, Poncelet F, Golinval J C. Physical interpretation of independent component analysis in structural dynamics [J]. Mechanical Systems and Signal Processing,2007,21(4):1561-1575.

[ 5 ] McNeil S. Modal identification using blind source separation techniques [D]. Houston: University of Houston, 2007.

[ 6 ] Donoho D L. De-noising by soft-Thresholding[J]. IEEE Transactions on Information theory,1995,41(3):613-615.

[ 7 ] 李洪,郝豪豪,孙云莲.具有独立分量的经验模态分解算法研究[J]. 哈尔滨工业大学学报,2009,41(7): 245-248.

LI Hong, HAO Hao-hao, SUN Yun-lian. Improved algorithm for empiricalmode decomposition with independent elements [J].Journal of Harbin Institute of Technology,2009,41(7):245-248.

[ 8 ] 静行,刘真真,原方.随机激励下基于ICA的结构模态参数识别[J].噪声与振动控制, 2014, 34(6):178-183.

JING Hang, LIU Zhen-zhen, YUAN Fang. Structural model parameter identification based onICA under random excitation [J].Noise and Vibration Control, 2014, 34(6):178-183.

[ 9 ] 张晓丹.基于盲源分离技术的工程结构模态参数识别方法研究[D].北京:北京交通大学,2010.

[10] Box G E P, Jenkins G M, Reinsel G C. Time series analysis, forecasting and control[M].Englewood Clifs, NJ, Prentice Hall,1994.

[11] 张建伟，江琦，赵瑜，等.一种适用于泄流结构振动分析的信号降噪方法[J].振动与冲击, 2015, 34(20): 179- 184.

ZHANG Jian-wei, JIANG Qi, ZHAO Yu, et al. De-noising method for vibration signal of flood discharge structure[J].Journal of Vibration and Shock, 2015 ,34(20): 179-184.

[12] 崔拥军，熊晓燕，王峰. 应变模态参数曲线的结构损伤位置及程度研究[J]. 机械设计与制造,2013,8:85-87.

CUI Yong-jun， XIONG Xiao-yan， WANG Feng. Study of damage location and degree of structural strain modal parameter curve [J]. Machinery Design & Manufacture,2013,8:85-87.

Application of a combined technique of wavelet and ICA in strain damage identification of hydraulic structures

ZHANG Jian-wei, BAO Zhen-lei, JIANG Qi

(School of Water Resources, North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

Aiming at the problem that modal parameters of a structure under environmental are identified difficultly, a combined technique of wavelet threshold and independent component analysis (ICA) modal parameter identification method of hydraulic structures was proposed. Firstly, a part of noise was filtered out with the wavelet threshold to reduce environmental excitation interferences to independence of each response component and make them meet the ICA separation assumption. Then structural modal parameters were identified by using ICA. The damage identification of a hydraulic structure was realized through comparing its strain modal parameters under different working conditions. This method was used in a cantilevered beam model test under water current excitation. The results showed that the combined technique of wavelet threshold and ICA can effectively identify modal parameters of a hydraulic structure; the difference of strain modal parameters can be used to identify if there is a damage in a structure; this proposed method can effectively solve the problem of modal parameter identification for large hydraulic structures under environmental excitation. The results provided a reference for safe operation and on-line monitoring of structures.

ambient excitation; hydraulic structure; wavelet analysis; independent component analysis (ICA); damage identification

10.13465/j.cnki.jvs.2016.11.028

国家自然科学基金(51009066)；河南省高等学校青年骨干教师资助计划(2012GGJS-101)；河南省科技攻关(142102310122;142300410177;132102310320)

2015-07-30修改稿收到日期：2015-12-02

张建伟 男，博士，1979年生

TV31

A