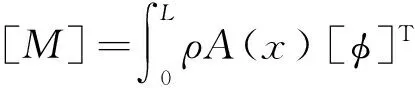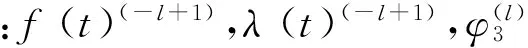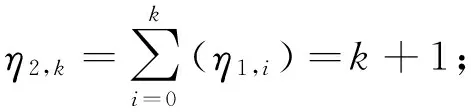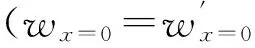基于样条有限点法的变截面Euler梁横向自由振动分析

刘　鹏， 刘红军， 林　坤， 秦　荣

(1. 哈尔滨工业大学 深圳研究生院,广东 深圳　518055；2.广西大学 土木建筑工程学院,南宁　530004)

基于样条有限点法的变截面Euler梁横向自由振动分析

刘鹏1， 刘红军1， 林坤1， 秦荣2

(1. 哈尔滨工业大学 深圳研究生院,广东 深圳518055；2.广西大学 土木建筑工程学院,南宁530004)

基于Bernoulli-Euler梁理论，采用样条有限点法建立考虑截面高宽度沿轴线性变化的变截面Euler梁振动分析的计算模型，通过沿梁轴线设置一定数量的样条节点对变截面梁样条离散化，采用三次B样条函数对梁的位移场进行插值，基于Hamilton原理导出变截面Euler梁的振动方程，推导考虑截面尺寸变化效应的总刚度和总质量矩阵的表达式，并编制计算程序，算例分析表明，模型的变截面梁的横向自振频率解答与文献解答吻合良好，计算精度和计算效率高，且模型边界处理简单，取样条离散节点数为15时，模型可以取得较高精度且解答趋于稳定。模型可适用于不同边界、不同截面变化率和不同截面类型的变截面Euler梁的自由振动分析。

欧拉梁理论；变截面梁；横向自由振动；样条有限点法

梁结构是工程中重要的结构，在土木、桥梁及航空航天等领域，梁式结构得到广泛运用，梁的振动问题也是工程结构中重要问题，对长细比较小的细长梁，基于Bernoulli-Euler梁理论(EBT)建立动力分析模型可以满足工程精度要求[1]。变截面梁截面的不确定性，使得其建模与分析方法与等截面梁不同，等截面Euler梁自由振动分析已经具有解析解，而变截面Euler梁自由振动分析尚无统一解析解[2]。为此，研究人员们针对变截面Euler梁振动分析提出了各类数值和建模方法研究，如有限差分法[3-4](FDM)，微分变换法[5](DTM)、微分变换单元法[1](DTEM)、修正耦合应力理论[6](MSCT)及其他数值分析方法[2, 7-8]等。

秦荣[9-11]提出用于结构分析的样条有限点法(Spline Finite Point Method,SFPM),研究表明SFPM具有不需划分结构单元，边界处理方便，计算精度和效率较高等优点，可对各类梁、板、桥梁等结构进行分析[12-14]。对变截面Euler梁结构的振动问题, 并未见有文献报道采用SFPM进行建模分析。基于SFPM的优点，本文针对截面高宽和宽度沿轴线方向线性变化的变截面Euler梁，采用SFPM建立其振动分析模型，首次推导其考虑梁截面尺寸变化效应的刚度矩阵和质量矩阵的整体表达式，通过算例分析研究截面尺寸变化效应对变截面Euler梁的横向自由振动频率的影响，并与文献计算结果比较，验证本文方法的正确性。

1变截面Euler梁SFPM计算模型

1.1Euler梁理论

如图1所示变截面梁，假定弹性模量E和材料密度ρ均沿着梁轴线为常数，梁跨为L，梁横截面面积A(x)和惯性矩I(x)沿着梁轴线按幂函数连续变化。根据EBT理论，在受外部横向荷载p=p(x,t)作用下，设变截面Euler梁的横向位移设为w=w(x,t)，可得变截面Euler梁的位移、应变、应力的表达式为：

(1)

图1　变截面梁示意图Fig.1 The sketch of tapered beams

(2)

(3)

式中：cb,ch,cd分别为与b(x),h(x),d(x)相关的截面变化系数；cb=ch=cd=0表示为等截面梁；A0,I0为变截面梁左端的截面面积和惯性矩。

由式(1),(2)展开，可得：

(4)

基于Hamilton原理，可得不考虑阻尼作用下变截面Euler梁的运动总势能泛函为[11]：

(5)

1.2变截面Euler梁SFPM计算格式

基于SFPM的建模离散方法[10]，对图1所示的变截面Euler梁 沿轴线x方向进行样条离散，并对梁进行均匀划分，设N为样条离散节点个数，hx为样条离散步长，离散示意图如图2所示。

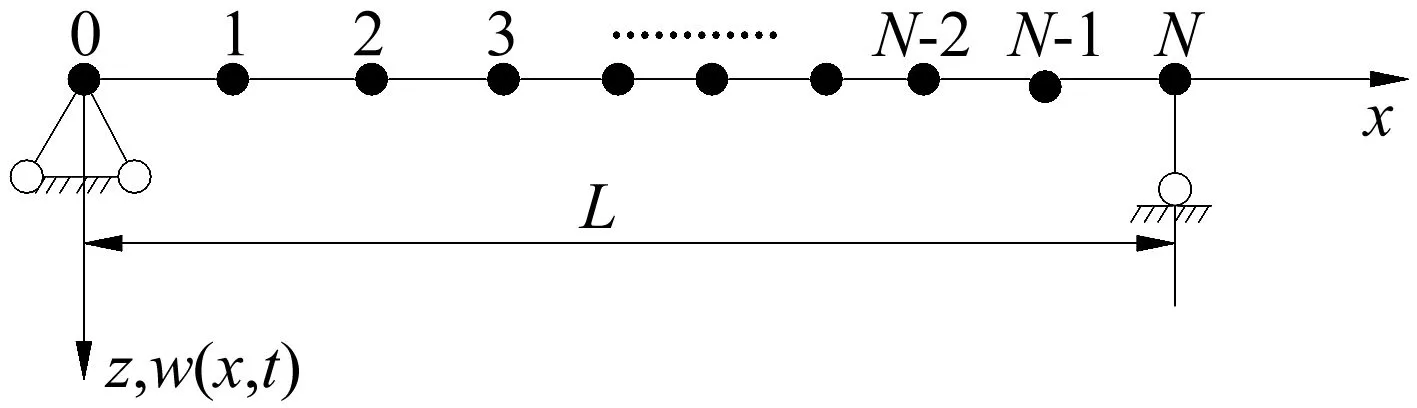
图2　变截面沿轴线梁样条离散化Fig.2 Spline discretization of tapered beam

图2中，有：

0=x0

xi=x0+ihx,hx=L/N

(6)

采用三次B样条函数对变截面Euler梁的横向位移场w(x,t)进行插值，有：

w=w(x,t)=[φ(x)]{a(t)}=[φ]{a}

(7)

式中：

(8)

式中[φ]为一组由三次B样条函数构成的样条基函数；{a}为样条节点广义参数。本文采用广义参数法构造出适合各种边界条件的样条基函数[10-11]，将[φ]展开可写为：

[φ]=[φ-1φ0φ1…φNφN+1]=

[φ3,-1φ3,0…φ3,Nφ3,N+1][Qs]=

[φ3,i]1×(N+3)[Qs]

(9)

式中：[Qs]为(N+3)×(N+3)阶的转换矩阵；φ3,i为与样条节点和离散步长相关的3次B样条函数，可展开为：

(i=-1,0,…,N,N+1)

(10)

[Qs]=diag([g],[I],[h])

(11)

式中：[I]为(N-3)×(N-3)阶的单位矩阵

本文采用的样条基函数[φ]满足边界条件[10]

(13)

对式(7)求导，得：

(14)

将式(7)、(14)代人式(5)得变截面Euler梁的运动样条离散化后的总势能泛函为

(15)

式中

(16)

(17)

(18)

对式(14)，利用变分原理，可得

δΠ=∂Π/∂{a}=0

(19)

得到变截面Euler梁样条离散化的弯曲振动方程

(20)

若外荷载为零，可得变截面Euler梁样条离散化的自由振动方程为：

(21)

假定变截面Euler梁轴线上各节点均按相同的频率作简谐振动，并令{a}={φ}sin(ωt+θ)，并代人式(21)，可得频率方程为：

([K]-ω2[M]){φ}={0}

(22)

式中令λ=ω2，则式(22)可化为

([K]-λ[M]){φ}={0}

(23)

式(23)即为变截面Euler梁自由振动问题的特征方程，为使式(23)有非零解，则必有

(24)

1.3刚度矩阵、质量矩阵计算

将式(4)代人式(16)、(17)，可得变截面Euler梁的刚度矩阵和质量矩阵的展开式为：

(25)

(26)

式中：

i,k=-1,0,1,…,N,N+1

(27)

其中Ax,m,Fx,n为(N+3)×(N+3)阶矩阵，是本文模型的重要矩阵，也是推导本文模型变截面Euler梁振动方程的关键步骤，可采用分部积分法进行计算，详见本文后节推导。

[K]=EI0[Ax0],[M]=ρA0[Fx0]

(28)

1.4分部积分计算

假定t=x/hx-i,c=k-i,0

(29)

并假设

(30)

代人式(27)中，可得各矩阵的积分计算式为：

(31)

i,k=-1,0,1,…,N,N+1

(32)

当m=n=0时，将式(30)～(32)展开并进行分部积分运算，可得：

f(t)=φ″3(t-c)λ(t)=φ3(t-c)

(33)

(34)

(35)

同理，当m=n=2时，将式(30)～(32)展开并进行积分运算， 可得

f(t)=f1(t)φ″3(t-c)f1(t)=(t+i)2

λ(t)=λ1(t)φ3(t-c)λ1(t)=(t+i)2

k=0,1,2

(36)

(37)

f(t)(-j)=∫f(t)(-j+1)dt=

(38)

(39)

λ(t)(-j)=∫λ(t)(-j+1)dt=

j=1,2,3,4

(40)

当m,n取其它值时，可按同样方法计算，限于篇幅本文不在展开计算，将所有计算得到的各矩阵代人式(25)～(27)就可得到变截面Euler梁SFPM计算模型的刚度矩阵[K]和质量矩阵[M]。

2边界条件

在计算自振频率前，需先根据边界条件对刚度和质量矩阵进行边界处理。综合式(13)及样条基函数的特性[10-11]，变截面Euler梁的SFPM计算模型的边界条件按以下方式处理：

2) 满足广义参数a-1=0，就可保证梁左端简单支条件(wx=0=0)；

4) 满足广义参数aN+1=0，就可保证梁右端简支条件(wx=L=0)

以两端固定梁为例，处理广义参数a-1,a0,aN,aN+1所对应[K],[M]矩阵的前两行两列，就可满足变截面Euler梁两端固支边界条件；处理方法采用缩减矩阵法，即直接将[K],[M]中对应边界的行列直接删去，对两端固支梁，经过边界处理后的[K],[M]矩阵的缩减成(N-1)×(N-1)阶的矩阵。

3算例分析

分析各类变截面梁横向自由振动，计算其横向自由振动频率值。定义四种边界条件：两端固支(C-C)、两端简支(P-P)、一端固支一端简支(C-P)、一端固支一端自由(C-F)。

算例1等截面Euler梁 及SFPM模型计算精度讨论

据表1计算结果可知，等截面Euler梁各阶自振频率的SFPM解与解析解、文献解吻合良好，验证了本文模型对等截面Euler梁横向自由振动分析是可靠的；当取样条离散节点N≥15时，本文可获得较高的计算精度和计算效率。

表1　等截面Euler梁无量纲频率系数边界)

算例2高度变化宽度不变矩形变截面Euler梁自振频率计算

矩形变截面Euler梁 ，高度沿轴线线性变化，宽度不变，采用文献[7]算例2的参数L=1 m,b0×h0=0.01×0.03 m,bN×hN=0.01×0.01 m,E=2.1×1011N/m2,ρ=7 800 kg/m3，计算得到截面变化率：cb=0,ch=2/3

文献[7]中采用一种分段建模的数值方法，对该矩形变截面Euler梁的横向振动频率进行分析。

本文采用SFPM模型对文献算例进行验证，表2 给出了不同样条离散节点数N情况下，按本文方法建模分析得到的P-P边界矩形变截面Euler梁自振频率的解答，并给出误差比较。表3给出了C-C，C-F边界情况下矩形变截面Euler梁的频率解答和误差比较。

表2　矩形变截面Euler梁无量纲频率系数边界)

注：误差值是本文解N=15与文献NS=8解的差值

算例3直径变化圆形变截面Euler梁自振频率计算

圆形变截面Euler梁，材料参数同算例2，截面类型变为圆形截面，截面尺寸：L=1 m,d0=0.02 m,dN=0.01 m经计算得截面变化率：cd=0.5 m。表4给出按SFPM计算得到的P-P边界圆形变截面梁自振频率，并给出取不同样条节点数N情况下的计算值和与文献解[7]的误差比较；表5给出C-C和C-F边界条件下圆形变截面Euler梁的频率解答及误差比较。

表3　矩形变截面Euler梁无量纲频率系数

注：err1=(P1-R1)/R1×100%;err2=(P1-R2)/R2×100%;NS是梁分段数

表4　圆形变截面梁无量纲频率系数边界)

注：误差值是本文解(N=15)与文献NS=8解的差值

由表2～表5计算结果可知，本文模型计算得到变截面Euler梁横向振动频率SFPM解答与文献[7,15]

非常逼近，验证本文模型可以分析不同截面类型的变截面Euler梁的振动问题。

综合表2和表4计算结果可知，在样条节点数N取到15时，变截面Euler梁的自振频率解答已经收敛，继续增加节点数N对计算精度提升不明显。而通过表3、表5的数据可知，在较少的样条离散节点数(N=15)情况下, 本文模型解答具有很高的计算精度且能适用于不同边界条件。

文献[15]在取较多梁分段数(NS=128)计算模型的频率解答才与本文解答逼近(N=15),而本文模型无需要划分结构单元，只需设置适当的样条节点数，就可以获得很高的计算精度和计算效率，而且频率的计算精度与梁的长度无关，这也是本文模型的创新性所在。

注：err1=(P1-R1)/R1×100%;err2=(P1-R2)/R2×100%;NS是梁分段数

算例4高宽度同时变化时矩形变截面Euler梁自振频率计算

计算参数取自文献[4]，矩形变截面混凝土简支梁(P-P)，计算参数为：L=4 m,b0×h0=0.2×0.2 m,bN×hN=0.4×0.3 m,E=2.0×1010N/m2,ρ=2 500 kg/m3；计算得到截面变化率：cb=-1,ch=-0.5；文献[4]采用有限差分法建立变截面Euler梁的动力分析模型，该方法的计算精度主要取决于计算步长数n。本文采用SFPM进行建模分析，分析样条离散节点数对计算精度的影响，计算结果列于表6中。

表6　矩形变截面Euler梁无量纲频率系数边界)

注：误差值是本文解(N=15)与文献解(n=900)的差值

同时，采用本文SFPM建立模型(取N=15)，分析cb,ch变化对不同边界条件下变截面Euler梁的自振频率影响；表7给出cb,ch变化时P-P和C-F边界变截面Euler梁的前2阶频率系数；图3给出C-F边界变截面梁前2阶频率系数随cb,ch的变化曲线。

由表6计算结果可知，对截面高度宽度同时变化的矩形变截面梁，SFPM计算模型同样可以获得较高的计算精度，再次验证本文方法的正确性。

由表7计算结果及图3可知，不同边界条件条件下，变截面Euler梁的各阶频率随截面变化率cb或ch的变化呈现出不同的变化趋势：

(1) 对P-P边界变截面梁，保持cb不变，各阶频率均随ch的增大而明显减少，且比较ch=0.8与ch=0的频率值，可得1阶频率的平均减幅为52%，2阶频率的平均减幅为45%左右；而保持ch不变情况下，随cb的增大，除基频稍微减小外，P-P梁各阶频率均基本保持不变；

(2) 对C-F边界变截面梁，保持cb不变，随着ch的增大，1阶频率呈增大趋势，2阶频率呈减小趋势，比较ch=0.8与ch=0频率值，经计算可得1阶频率平均增幅为18%，2阶频率平均减幅为28.5%；而保持ch不变，各阶频率随着cb增大而增大，其中1阶频率增加较快，2阶频率增加较为平缓，比较cb=0.8与cb=0的频率值，可得 1阶频率的平均增幅为50%，而2阶频率的平均增幅为17%。

本文作者也分析了cb,ch的变化对C-C和C-P边界变截面Euler梁的横向自振自由振动的影响，结果表明： 与P-P边界类似，C-C和C-P边界变截面Euler梁的自振频率随ch增大(cb不变)而明显减小，平均减幅为在35%-45%之间；当cb增大(ch不变)时，除C-P梁的第1、第2阶频率随cb增大而有微小增大外，C-C和C-P梁的自振频率均随cb增大(ch不变)而基本保持不变。可见，不同边界条件下，变截面梁的横向自振频率随截面变化率cb,ch变化呈现出不同的变化趋势。

表7　不同截面变化率cb,ch下 矩形变截面Euler梁无量纲频率系数 i

图3　C-F边界变截面Euler梁的频率系数随cb,ch的变化Fig.3 Variation of the non-dimensional frequencies for clamped-free (C-F) tapered Euler beam with respect to the variation of taper ratio (cb,ch)

4结论

本文基于SFPM建立变截面Euler梁的振动分析的计算格式：

(1) 首次基于SFPM推导出截面高度、宽度线性变化的变截面Euler梁的振动分析模型，给出其整体刚度和质量矩阵的表达式；本文模型具有边界简单，程序编制方便，计算精度和效率高的优点，可适用于不同边界、不同截面变化率情况下的变截面梁的自由振动问题。对其他更高阶次截面变化类型的变截面梁的振动分析，本文方法同样适用。

(3) 本文模型计算精度与样条节点数N取值相关，与梁跨度L无关。当取N=15时，变截面梁的横向自振频率解答已经收敛且保持稳定，继续增大N值，对计算精度提升影响不大。

(4) 不同边界条件下，变截面Euler梁的横向自振频率随截面高度和宽度变化率的变化呈现出不同的变化趋势。

[ 1 ] Shahba A, Rajasekaran S. Free vibration and stability of tapered Euler-Bernoulli beams made of axially functionally graded materials[J]. Applied Mathematical Modelling, 2012,36(7):3094-3111.

[ 2 ] 周叮. 一类变截面梁横向自由振动的精确解析解[J]. 振动与冲击, 1996, 15(3):12-15.

ZHOU Ding. The exact analytical solution of transverse free vibration of a type of beams with variable cross-sections[J]. Journal of Shock and Vibration, 1996, 15(3):12-15.

[ 3 ] 朱由锋, 朱由国. 基于有限差分法的变截面旋转梁弯曲振动[J]. 噪声与振动控制, 2014, 34(3):6-10.

ZHU You-feng, ZHU You-guo, Analysis of bending vibration of rotating tapered beams base on finite difference method[J] Noise and Vibration Control, 2014, 34(3):6-10.

[ 4 ] 钱波, 岳华英. 变截面梁横向振动固有频率数值计算[J]. 力学与实践, 2011, 33(6):45-49.

QIAN Bo, YUE Hua-ying, Numerical calculation of natural frequency of transverse vibration of non-uniform beams[J].Mechanics in Engineering, 2011, 33(6):45-49.

[ 5 ] Ozgumus O O, Kaya M O. Flapwise bending vibration analysis of a rotating tapered cantilever Bernoulli-Euler beam by differential transform method[J]. Journal of Sound and Vibration, 2006,289(1):413-420.

[ 7 ] 崔灿, 蒋晗, 李映辉. 变截面梁横向振动特性半解析法[J]. 振动与冲击, 2012, 31(14):85-88.

CUI Can, JIANG Huan, LI Ying-hui, Semi-analytical method for calculating vibration characteristics of variable cross-section beam [J]. Journal of Shock and Vibration,2012,31(14):85-88.

[ 8 ] Huang Y, Li X. A new approach for free vibration of axially functionally graded beams with non-uniform cross-section[J]. Journal of Sound and Vibration, 2010,329(11):2291-2303.

[ 9 ] 秦荣. 样条有限点法[J]. 广西大学学报, 1980, 5(2):18-35.

QIN Rong. Spline finite point method[J].Journal of Guangxi University, 1980,5(2):18-35.

[10] 秦荣. 结构力学中的样条函数方法[M]. 南宁: 广西人民出版社, 1984.

[11] 秦荣. 样条无网格法[M]. 北京: 科学出版社, 2012.

[12] 李秀梅, 李萍, 黄幸, 等. 连续梁分析的样条有限点法及程序设计[J]. 广西大学学报:自然科学版, 2014, 39(4):732-739.

LI Xiu-mei, LI Ping, HUANG Xing, et. al, Spline finite point method for continuous beam analysis and program design[J].Journal of Guangxi University, 2014, 39(4):732-739.

[13] 秦荣. 复合材料板壳分析的样条有限点法[J]. 工程力学, 2001,18(1):14-22.

QIN Rong. Analysis of composite plate and shell based on spline finite element method [J].Engineering Mechanics, 2001,18(1):14-22.

[14] 秦荣, 王建军, 李秀梅. 箱拱桥梁地震反应分析的新方法研究[J]. 工程力学, 2009, 26(5):148-152.

QIN Rong, WANG Jian-jun, LI Xiu-mei. Study on new method for seismic response analysis of box arch bridge [J]. Engineering Mechanics, 2009, 26(5):148-152.

[15] 崔灿. 变截面梁振动特性快速算法及其应用[D]. 成都：西南交通大学, 2012:1-78.

Free transverse vibration analysis of tapered bernoulli-euler beams based on spline finite point method

LIU Peng1, LIU Hong-jun1, LIN Kun1, QIN Rong2

(1. Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China;2. College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China)

Based on Bernoulli-Euler beam theory, a new model was presented here to study free transverse vibration problems of tapered Euler beams by using the spline finite point method (SFPM) considering both width and height of beams’ cross section linearly varying along the axial direction. With the proposed method, a beam was discretized by a set of uniformly scattered spline nodes along the axis direction instead of meshes, and the cubic-B spline interpolation functions were utilized to approximate the displacement filed of the beam. The free vibration equation of the beam was derived base on Hamilton Principle, and the global stiffness and mass matrices for the tapered beam were deduced in detail. The results of examples showed that the solutions to natural frequencies of tapered beams based on the proposed method are good in agreement with those reported in literatures; the proposed method has a higher accuracy, a lower computational cost and an easier way for boundary treatment; the solutions with a higher accuracy can be achieved by selecting the spline node number of no less than 15; the presented model is suitable for the free transverse vibration of tapered beams with various cross-section types, tapered ratios and boundary conditions.

Bernoulli-Euler beam theory; tapered beam; free transverse vibration; spline finite point method

10.13465/j.cnki.jvs.2016.11.011

国家自然科学基金(51178153)

2015-09-17修改稿收到日期：2015-12-02

刘鹏 男，博士生，1983年生

刘红军 男，教授，博士生导师，1968年生

E-mail：liuhongjun@hit.edu.cn

TU311.3

A