桥梁断面两个涡振锁定区间的数值模拟研究

黄　俐， 周　帅， 梁　鹏

(1. 华南农业大学 水利与土木工程学院，广州　510642；2.湖南大学 风工程试验研究中心，长沙　410082;3. 中交四航局第一工程有限公司，广州　510310)

桥梁断面两个涡振锁定区间的数值模拟研究

黄俐1， 周帅2， 梁鹏3

(1. 华南农业大学 水利与土木工程学院，广州510642；2.湖南大学 风工程试验研究中心，长沙410082;3. 中交四航局第一工程有限公司，广州510310)

对于某类大宽高比桥梁断面或者钝体形式断面，在基于同一组试验参数的节段模型风洞试验中，能够实测到相同振型两个分离的涡振锁定区间现象，并且两个区间内振动频率一致，这与一个断面对应一个Strouhal数的理论不相符合。为了进一步研究这类非常规振动形式的气动机理，以一组宽高比为6的矩形断面为研究对象，基于风洞试验中实测的两个独立的涡振锁定区间响应数据，采用流体动力学软件Fluent开展了相应的数值模拟研究。数值计算获取了与风洞试验一致的两个独立分离的涡振锁定区间风振曲线，并且在区间跨度以及幅值关系上均吻合良好，然后通过Fluent提取了前后两个涡振锁定区间内的气动力和尾流漩涡进行了对比研究。研究结果表明，第一个锁定区间内的尾流漩涡呈现出经典的卡门涡街形态，第二个区间内的尾流涡模态则主要表现为非典型的“鱼尾摆动”形态，两个涡振区间的尾流形态完全不同；在两个独立的锁定区间内，气动升力与位移响应之间始终存在着相位差，并且均随着锁定区间的发展而持续增大，第一个锁定区间相位差的跳跃程度明显大于第二个锁定区间。

桥梁；涡振；锁定区间；数值模拟；尾流漩涡

涡激共振是钝体结构在来流作用下的一种常见的振动形式，是由于结构尾流中交替脱落的漩涡频率与结构固有频率重合而引起的一种流固耦合共振现象，其显著特征就是共振区间锁定和振动限幅[1-3]。针对特定的结构断面，尾流的漩涡脱落频率和来流风速之间可以通过Strouhal数进行换算，一种结构断面对应一个Strouhal数，利用该参数值可以实现对结构涡振锁定区间起振临界风速的估算，这是目前关于涡振研究的一般性结论[4]。

然而，对于某类大宽高比的桥梁断面，例如我国的苏通长江大桥的主梁断面，在节段模型风洞试验中，+5°风攻角的来流状态下，随着试验风速的增加，实测到了节段模型系统扭转自由度两个分离的涡激共振锁定区间，并且两个锁定区间内的振动卓越频率均与模型固有频率一致，也即说明苏通桥主梁断面在+5°风攻角来流下对应两个不同的Strouhal数，这与一个截面对应一个Strouhal数的结论是相矛盾的[5-7]。

对于苏通桥主梁断面风洞试验中实测到的这类两个锁定区间的涡振现象，在大宽高比的矩形断面的研究中也很容易观察到。文献[8]系统研究了宽高比在2.04.0的试验工况中均能实测到两个分离的涡振锁定区间。

Matsumoto[9]针对这类涡振现象开展研究，研究结论认为是结构表面运动涡与尾流卡门漩涡相互作用导致了多个涡振锁定区间的出现，即，来流在结构断面前沿分离，一部分在结构表面再覆并以一定的速度(大约为来流速度的60%)沿结构表面运动最终在尾流脱落，另一部分在尾流直接脱落形成卡门漩涡，运动涡的加入改变了原有卡门漩涡固有的脱落频率，从而改变了结构断面的Strouhal数，并且由于运动涡的脱落频率与来流速度相关，因此，该研究认为同一种结构断面在不同的来流速度下会对应不同的Strouhal数。

Tamura[10]针对两自由度尾流振子涡激力模型开展了相关研究，对涡激振动的气动机理进行了数学的描述，并明确了数学模型中的每个参数均进行了物理意义的解释。

为了进一步研究这类振动的气动机理，本文基于一组宽高比为6的矩形断面开展研究，通过CFD数值模拟来观察前后两个分离的涡振锁定区间内气动力、位移响应以及尾流漩涡形态之间的对应关系。

1模型参数与试验结果

针对宽高比为6的矩形断面，Chen等[9]开展了刚性节段模型风洞试验研究，模型的基本参数如表1所示。弹性悬挂刚性节段模型风洞试验结果如图1所示，从图中可以看出两个竖向自由度分离的涡振锁定区间区间，并且试验实测到两个锁定区间内的振动卓越频率均与模型的固有频率5.90 Hz基本保持一致。根据前后两个涡振锁定区间的起振风速，振动卓越频率以及横风向尺寸得出对应的两个Strouhal数分别约为0.2和0.1，而第二个锁定区间对应的Strouhal数0.1与欧洲抗风规范中的参考值0.06更为接近[12]。在涡振幅值关系上，前一个涡振锁定区间的幅值约为后一个区间的0.5倍。

图1　风洞试验实测风振响应曲线Fig.1 Wind tunnel tests measured wind induced oscillation curves

参数类型数值长度L/mm1530横风向尺寸D/mm40顺风向尺寸B/mm240试验风速U/(m·s-1)<6等效质量m/(Kg·m-1)3.25横风向固有基频f0/Hz5.90阻尼比ξ00.0058Scruton数Sc121Reynolds数Re6293

2数值模拟方法

CFD数值模拟基于流体动力学软件Fluent展开，首先，采用Gambit进行计算区域的规划、计算网格的划分以及边界条件的设置。如图2(a)所示，矩形断面的2D模型布置在计算域的中心位置，近壁面为四边形刚性网格区域(包括四边形正交贴体网格和外围Pave网格，如图2(b)所示)，计算域外围是完全正交的四边形结构网格区域，介于外围结构网格和近壁面刚性网格之间的是三角形动网格区域，整个计算域共生成了31 590个计算网格，壁面Yplus在3.5以内。

采用Newmark-β方法对矩形断面计算模型的动力特性进行模拟，首先，根据模型的质量、阻尼和刚度参数编写模型振动的竖向和扭转两自由度迭代程序；然后以User Define Function (UDF)的方式在Fluent求解器中进行编译。

针对计算模型的Fluent流固耦合分析过程中，采用k-ωSST湍流模型，加载UDF，迭代计算按照以下步骤循环进行：第一步，对当前计算时间步模型壁面遍历积分提取竖向和扭转自由度气动力；第二步，根据UDF程序计算出模型在当前时间步竖向和扭转自由度的运动位移和速度；第三步，DEFINE-CG-MOTION宏强迫模型按当前时间步计算得到的结果产生相应位移并促使动网格区域的网格重划分，形成下一时间步新的计算域。计算结果是否稳定通过观察迭代计算残差和响应时程曲线来判断。

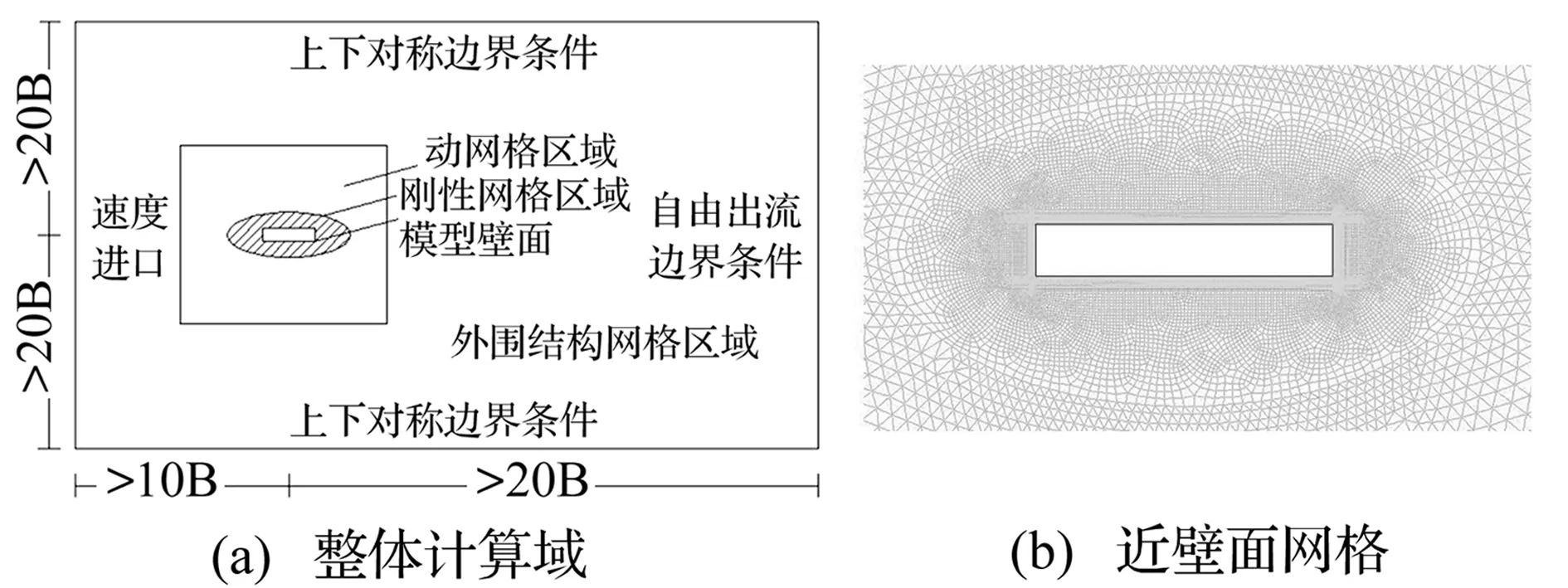
图2　计算网格Fig.2 Calculation cells

3计算结果

3.1位移响应

CFD数值计算得到的模型竖向自由度位移幅值响应曲线与试验实测曲线对比如图3所示。横坐标为无量纲风速，f0为模型竖向自由度固有频率5.90 Hz，从下文的时程曲线和频谱中可以观察到涡振锁定区间内模型竖向自由度的振动卓越频率与固有频率是基本一致的，U为来流风速，D为模型横风向特征尺寸，D=40 mm；纵坐标为无量纲幅值，即，位移响应幅值与模型横风向特征尺寸的比值，位移响应幅值采用固定时间长度(55 s)位移时程曲线取根方差乘以根号2的方式确定。

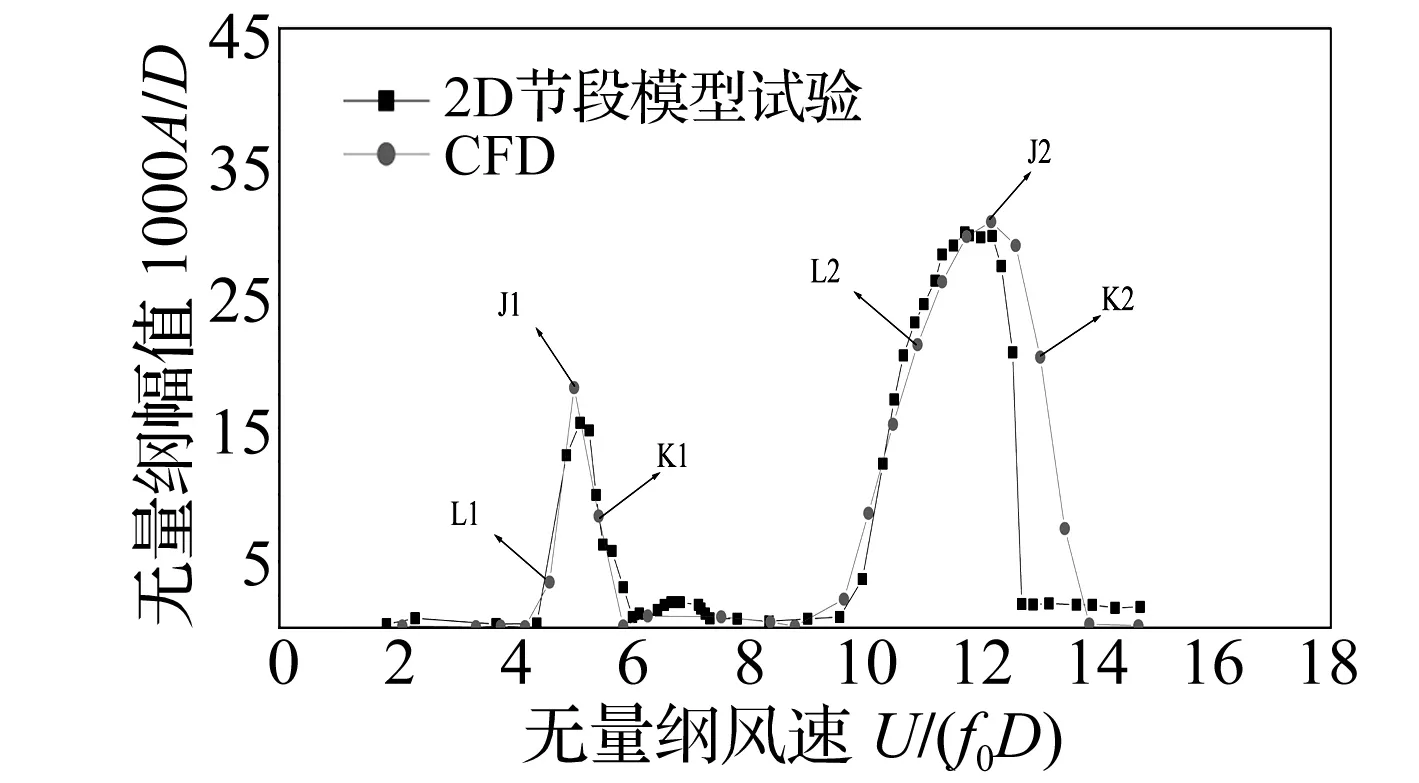
图3　风振响应曲线试验值与CFD计算值对比Fig.3 The comparison of wind induced oscillation curves between experimental and calculation results

从图3中可以看出，基于风洞试验模型参数开展的数值计算同样观察到了两个分离的涡振锁定区间现象，并且在锁定区间无量纲风速跨度和幅值关系上，计算值与试验实测值吻合良好。为了能进一步研究前后两个锁定区间内气动力以及尾流涡等参数的变化特征，特选定数值计算结果中6个特征响应点的计算结果进行分析。如图3所示，L1、J1、K1对应第一个涡振锁定区间的上升点、幅值点和下降点；L2、J2、K2则分别对应第二个涡振锁定区间的三个区间特征点。

另外，在动力自由度关系上，CFD数值计算模型与风洞试验刚性节段模型是一致的，基于风洞试验模型竖向和扭转自由度的实际参数，数值计算模型同样分别设置了竖向和扭转两个自由度。数值计算过程中也获得了模型扭转自由度的相关响应数据，由于模型在竖向和扭转两自由度振动状态下，实际振动中竖向自由度响应绝对占优。在现有的计算工况中扭转自由度的位移响应幅值均在0.2°以下，基本可忽略，限于篇幅，不再详细展开讨论。

第一个涡振锁定区间内特征响应点L1、J1、K1竖向自由度位移响应时程和频谱如图4～图6所示。从图中可以看出，三个特征响应点的位移时程均为等幅状态，而振动卓越频率分别为5.82 Hz、5.88 Hz和5.85 Hz，均与模型竖向自由度固有频率5.90 Hz基本保持一致，可定性为等幅涡振。

图7～图9分别对应第二个涡振锁定区间内L2、J2、K2特征响应点。从图中同样可观察到与第一个锁定涡振区间一致的响应特征：位移响应时程基本为等幅状态，卓越频率分别为5.86 Hz、5.98 Hz、5.98 Hz，与模型固有频率5.90 Hz基本一致。

特征响应点J1和 J2分别对应第一个和第二个涡振锁定区间的涡振幅值点，无量纲幅值分别为18.0/1 000和30.5/1 000，对应来流风速分别为5.0 m/s和12.2 m/s，振动卓越频率分别为5.88 Hz和5.98 Hz，并且对应同一模型断面，横风向特征尺寸均为40 mm，因此，按照Strouhal定律可以计算得到两个不同的参数值，分别为0.2和0.08。

3.2尾流漩涡形态

3.2.1第一个锁定区间

第一个涡振锁定区间内特征响应点L1、J1和K1对应风速下单个振动周期内尾流漩涡形态变化如图10～图12所示。起振点L1振幅较小，尾流漩涡脱落也不明显；J1测点对应第一个涡振锁定区间的幅值点，尾流呈现出了明显的卡门漩涡脱落特征，单个振动周期内有两个漩涡分别从模型的上下表面脱落，形成了竖向自由度的简谐气动升力；K1对应着锁定区间的下降段，单个振动周期内，尾流漩涡脱落总体上也表现出了卡门涡街特征，但漩涡特征相对于J1测点已经明显弱化[13]。

3.2.2第二个锁定区间

第二个涡振锁定区间单个振动周期内L2、J2、K2特征响应点的尾流变化分别如图13～图15所示。而从图中可以观察到，与第一个锁定区间出现的卡门漩涡特征明显不同的是，第二个锁定区间内三个特征响应点的尾流特征没有漩涡脱落，而是表现出“鱼尾摆动”的形态，尾流摆动幅度与模型振动位移幅值是正相关的关系。值得注意的是，同一个结构断面出现两个涡振锁定区间通常发生在截面宽高比大于4的扁平的钝体断面。本文研究的矩形断面宽高比为6，所观测到的第一个锁定区间为卡门涡街尾流形态，而第二个锁定区间内的尾流中卡门涡街不明显而呈现出“鱼尾摆动”，这实际上与文献中Tamura两自由度尾流振子模型中描述的涡激振动形成机理较为吻合，前后两个涡振锁定区间的Reynolds数相差将近两倍，这可能就是尾流形态发生改变的原因之一[14-15]。

图4 测点L1竖向自由度响应Fig.4DynamicresponsesofverticalDOFofpointL1图5 测点J1竖向自由度响应Fig.5DynamicresponsesofverticalDOFofpointJ1图6 测点K1竖向自由度响应Fig.6DynamicresponsesofverticalDOFofpointK1

图7 测点L2竖向自由度响应Fig.7DynamicresponsesofverticalDOFofpointL2图8 测点J2竖向自由度响应Fig.8DynamicresponsesofverticalDOFofpointJ2图9 测点K2竖向自由度响应Fig.9DynamicresponsesofverticalDOFofpointK2

图10 单个振动周期内测点L1尾流漩涡形态变化规律Fig.10ThevorticeschangingrulesinoneoscillationcycleofpointL1图11 单个振动周期内测点J1尾流漩涡形态变化规律Fig.11ThevorticeschangingrulesinoneoscillationcycleofpointJ1图12 单个振动周期内测点K1尾流漩涡形态变化规律Fig.12ThevorticeschangingrulesinoneoscillationcycleofpointK1

3.3气动力响应

图16为数值计算得到的竖向自由度频比响应曲线，图中横坐标为无量纲风速，纵坐标为频率比值响应，即不同风速下模型尾流漩涡脱落或者摆动频率与模型竖向自由度固有频率的比值。从图中可以观察到两个明显的涡振锁定区间，在这两个区间内，尾流频率与模型固有频率基本一致，在整个区间内锁定，而在区间外，尾流频率随风速的增加而呈线性增长趋势，符合Strouhal定律的特征。

图13 单个振动周期内测点L2尾流漩涡形态变化规律Fig.13ThevorticeschangingrulesinoneoscillationcycleofpointL2图14 单个振动周期内测点J2尾流漩涡形态变化规律Fig.14ThevorticeschangingrulesinoneoscillationcycleofpointJ2图15 单个振动周期内测点K2尾流漩涡形态变化规律Fig.15ThevorticeschangingrulesinoneoscillationcycleofpointK2

图16　涡振锁定区间频率响应曲线Fig.16 Frequency response curves in vortex-induced vibration curves

图17为数值计算得到的相位差响应，横坐标同样为无量纲来流风速，而纵坐标则为气动升力与竖向自由度位移响应之间的相位差。从图中可以看出，在两个分离的涡振锁定区间内，随着涡振区间的发展，气动升力与位移响应之间均存在着相位差，并且不是恒定的，表现出随着锁定区间的发展而逐步增大的特征，也即说明在同一个涡振锁定区间内，气动升力与位移响应之间的相位差是在不断增大的。以第一个涡振锁定区间为例，图18对应L1、J1和K1三个特征响应点的气动升力时程与位移响应时程的对应关系，随着涡振区间的发展，位移响应幅值先增大后减小，气动升力幅值也是先增大后减小，而气动升力与位移响应之间的相位差却是在持续增大的。L1和J1测点处相位差基本在30°以内，气动升力总体上在为模型的振动提供能量，而当涡振区间发展到K1点，气动升力与位移响应之间的相位差已经达到120°，此时，气动升力实际上是在抑制着模型的振动。

图17　涡激气动力与位移响应相位差Fig.17 The phase differences between vortex shedding forces and displacement

图18　第一个涡振锁定区间内涡激气动力与位移响应相位差时程对比Fig.18 The time history of phase differences between vortex shedding forces and displacement of the first lock-in

4结论

(1) 采用Fluent流固耦合分析实现了模型风洞试验中观察到的两个分离的涡振锁定区间现象的数值模拟，在起振风速点、区间跨度以及涡振幅值关系上，计算值与试验实测值均吻合良好；

(2) 数值计算结果显示，第一个涡振锁定区间内的尾流总体呈现出卡门漩涡的形态特征，而第二个锁定区间内特征响应点的尾流中基本没有卡门漩涡对的出现，而是表现出“鱼尾摆动”的尾流形态，摆动幅度越大，模型位移响应幅值越大，并没有观察到明显的卡门涡与模型表面运动涡相互作用的现象；

(3) 两个涡振锁定区间内，气动升力与位移响应之间的相位差始终存在，并且随着涡振区间的发展而不断增大，在涡振区间的下降段，该相位差甚至达到120°，此时的气动力实际上是抑制模型振动的。

[ 1 ] 许福友,丁威, 姜峰,等. 大跨度桥梁涡激振动研究进展与展望[J].振动与冲击，2010, 29(10): 40-46.

XU Fu-you, DING Wei, JIANG Feng, et al. Research development and forward of vortex induced vibration on large span bridges [J]. Journal of Vibration and Shock，2010, 29(10): 40-46.

[ 2 ] 秦浩, 廖海黎, 李明水. 大跨度双幅连续钢箱梁桥涡激振动特性风洞试验研究[J].振动与冲击，2014, 33(14): 206-210.

QIN Hao, LIAO Hai-li, LI Ming-shui. Vortex induced vibration performance of long span continuous steel twin box beam bridge based on wind tunnel test[J]. Journal of Vibration and Shock，2014, 33(14): 206-210.

[ 3 ] 张志田, 陈政清. 桥梁节段与实桥涡激共振幅值的换算关系[J].土木工程学报，2011, 44(7): 77-82.

ZHANG Zhi-tian,CHEN Zheng-qing. Vibration amplitude relationship between practical bridge and section model[J]. Journal of Civil Engineering，2011, 44(7): 77-82.

[ 4 ] 陈政清. 桥梁风工程 [M].北京: 人民交通出版社, 2005.

[ 5 ] 陈艾荣. 苏通桥主桥高雷诺数下涡激振动及三分力特性试验研究总报告[R]. WT-200418，上海：同济大学土木工程防灾国家重点实验室,2004.

[ 6 ] 陈艾荣,马如进,王达磊,等 基于性能的苏通大桥抗风设计[J]. 公路, 2009(5): 139-145.

CHEN Ai-rong, MA Ru-jin, WANG Da-lei, et al. Wind resistance design based on performance of Sutong bridge[J]. Highway，2009(5): 139-145.

[ 7 ] 陈艾荣,等. 苏通大桥风荷载研究[R]. 上海: 同济大学土木工程防灾国家重点实验室,2004.

[ 8 ] Garrett J L. Flow-induced vibration of elastically supported rectangular cylinders[D]. Iowa: Iowa State University,2003.

[ 9 ] Matsumoto M. Vortex shedding of bluff bodies: a review [J]. Journal of Fluids and Structures,1999, 13(1):791-811.

[10] Tamura Y, Matsui G. Wake-oscillator model of vortex-induced oscillation of circularcylinder[C]//Proceedings of the 5th international conference on wind engineering, Fort Collins, USA, July,1979.

[11] Chen Zheng-qing, Chen Wen, Hua Xu-gang, et al. Higher modes’ vertical vortex-induced vibrations of suspension bridges—Part 2: aeroelastic model study[C]// University of Nottingham. EACWE VII, Cambridge: University of Nottingham,2013.

[12] Eurocode: Actions on structures[S]. Brussels: CEN national Members, 2004.

[13] Sarpkaya T. A critical review of the intrinsic nature of vortex-induced vibrations [J]. Journal of Fluids and Structures, 2004,19(1): 389-447.

[14] Bearman P W, Gartshore I S, Maull D J, et al.Experiments on flow-induced vibration of a square section cylinder[J].J. fluids struct., 1987,1(1):19-34.

[15] Simiu E, Scanlan R H. Wind effects on structures-an introduction to wind engineering[M]. ThirdEdition,1996.

Numerical simulation for two separate vortex-induced vibration lock-in intervals of bridge sections

HUANG Li1, ZHOU Shuai2, LIANG Peng3

(1. College of Water Conservancy and Civil Engineering, South China Agricultural University, Guangzhou 510642, China;2. Wind Engineering Research Center, Hunan University, Changsha 410082, China;3. The First Engineering Company of CCCC Fourth Harbor Engineering Co. Ltd., Guangzhou 510500, China)

For some bridge sections or similar bluff bodies with a large aspect ratio, two separate vortex-induced vibration (VIV) lock-in intervals of the same model shape can be observed in the same section model wind tunnel tests, and the dominant oscillation frequencies of the two lock-in intervals are the same, these do not agree with the traditional Strouhal law. In order to get a further understanding aerodynamic mechanism of these oscillations, a rectangular section with an aspect ratio of 6 was taken as a study object, and based on its 2D section model wind tunnel tests parameters and results, Fluent-based numerical simulations were performed. The simulation results agree well with test ones in both lock-in ranges and amplitude responses. Then, more details about aerodynamic forces and wake vortices were obtained using the post processing of Fluent. The study showed that the wake vortices of the first VIV lock-in interval is the typical Karmen vortex mode, while the second one is full different from the first one, its wake vortices are observed to be “fish tail waving” mode; in the two separate lock-in intervals, there is always a phase difference between aerodynamic lift and vertical displacement response, and the phase difference continuously increases with developing of the lock-in interval; moreover, the jump of the phase difference of the first lock-in interval is bigger than that of the second one.

bridges; vortex-induced vibration; lock-in interval; numerical simulation; wake vortices

10.13465/j.cnki.jvs.2016.11.008

国家自然科学基金(91215302;51278189);广东省自然科学基金(2015A030310164)

2015-09-01修改稿收到日期：2015-12-04

黄俐 女，博士，讲师，1984年生

U446.1

A