紧性和正则性在迁移方程中的应用

吴红星，叶桂英，程国飞

（1.上饶师范学院数学与计算机科学学院，江西上饶334001；2.上饶县第三小学，江西上饶334101）

，由于

紧性和正则性在迁移方程中的应用

吴红星1，叶桂英2，程国飞1

（1.上饶师范学院数学与计算机科学学院，江西上饶334001；2.上饶县第三小学，江西上饶334101）

在L1空间中，利用算子理论、半群理论探讨了具抽象边界条件的非均匀介质的中子迁移算子的谱分布情况。在考虑扰动算子是正则的和边界算子是部分光滑的条件下，运用豫解算子等方法，论证了相应的迁移算子所生成的C0半群所产生的余项R9（t）在L1空间中的弱紧性，获得了该算子的点谱集仅由有限个具有限代数重数的离散本征值构成。

抽象边界条件；紧性；迁移方程；正则性；离散本征值

1955年，Lehner和Wing研究了无限平行板中的中子方程［1］，之后该迁移方程解的渐近行为研究以及该迁移算子谱分布情况研究成为许多数学爱好者感兴趣的课题［2－10］。2001年，Latrach等讨论了带反射边界条件的粒子单能迁移算子的谱分析［2］，论证了迁移算子生产C0半群，详细证明了该半群所产生的Dyson－Phillips展开式的二阶余项的紧性，得到了该迁移算子的谱分布形态。王胜华等在L1空间中讨论了一类带周期边界条件的连续能量和均匀介质的迁移算子的谱分析［3］，论证了相应迁移算子产生C0群V（t）（t≥0）以及其余项的紧性，获得了该迁移算子的谱分布等结果。文献［4］把文献［3］的结果推广到带反射边界条件的情况。文献［5］研究了种群细胞中的Rotenberg模型，运用构造算子、比较算子等方法论证了相应九阶余项R9（t）的紧性，获得谱的存在性等结果。受文献［5］的启发，本文探讨了无限平行板中具抽象边界条件的非均匀介质的迁移算子的谱分布，论证了相应的C0半群所产生的Dyson－Phillips展开式的余项R9（t）的弱紧性，获得该迁移算子的点谱集仅由有限个具有限代数重数的离散本征值构成。

1 预备知识

以下研究一类带抽象边界条件的连续能量和非均匀介质的迁移方程的初边值问题：

其中σ（x，v），k（x，v，μ，v＇，μ＇）分别表示G和D×D0上的有界可测函数。令X＝L1（D）表相域D上有界可测函数全体按范数构成的Banach空间。相空间Di，D0，边界空间Xi，X0，范数‖ψi‖Xi，‖ψ0‖X0和算子B及积分算子K的定义等见文献［4］。

假设（O1）：其中H＝αJ＋N，H＝αJ＋N，121β1212β2α≥0，β≥0，J1和J2都是紧算子，考虑豫解方程（λI－B）ψ＝φ得到，

其中Pλ，Qλ，Dλ和Dλ的定义见文献［7］。

假设（O2）：算子K在X上是正则算子.故可由有限秩算子逼近，从而得到：

其中θi（x）∈L∞（［－a，a］），fi（·，·）∈L1（D0），gi（·，·）∈L∞（D0），I为有限指标集.并令

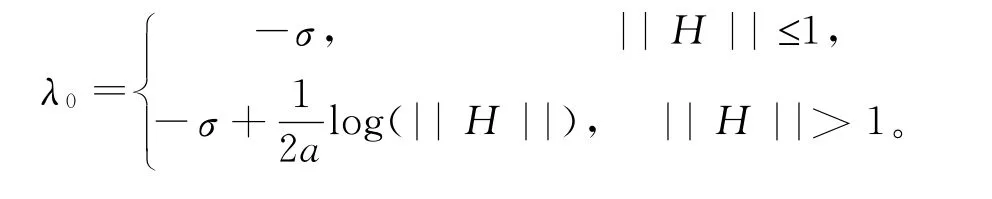
2 主要结果

引理2.1［6］假设T（其型为ω）是巴拿哈空间X中一个强连续半群的生成元，算子K是有界的，且存在m∈N，η＞ω，满足：

（1）对∀，Reλ＞η，（λI－T）－1［K（λI－T）－1］m是紧算子；

定理2.1 若假设（O1）和（O2）满足，则对任意r∈［0，1）有，

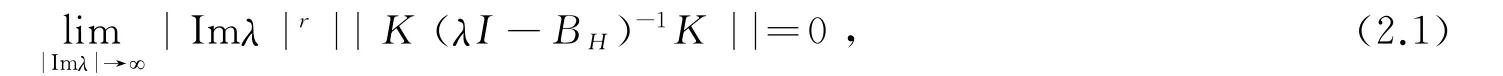
在Γ0＝｛λ∈C｜Reλ≥λ0＋ε｝（ε＞0）上一致成立。

证明 第一步：证明

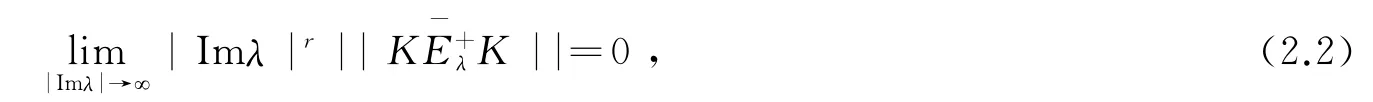
在Γ0上成立。对φ∈X，令，t＝x－μ＇s，可以得到

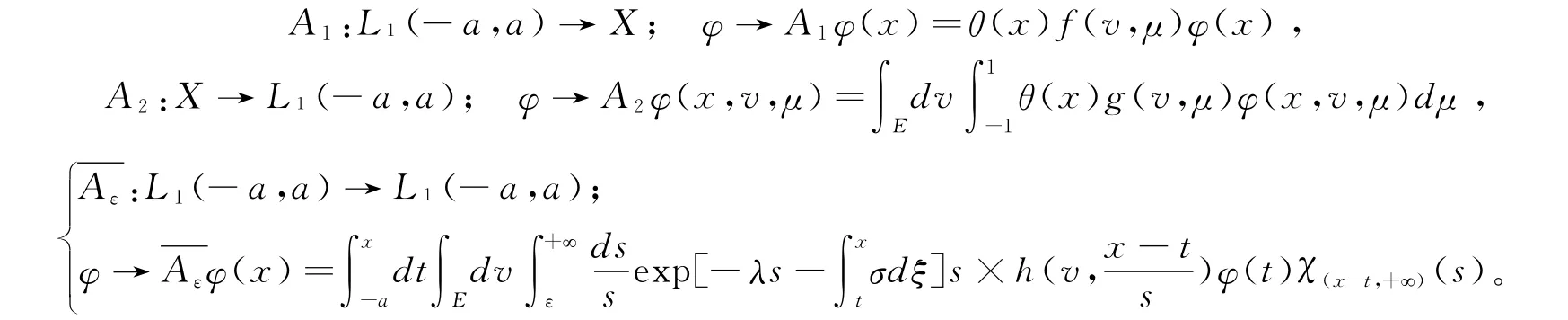
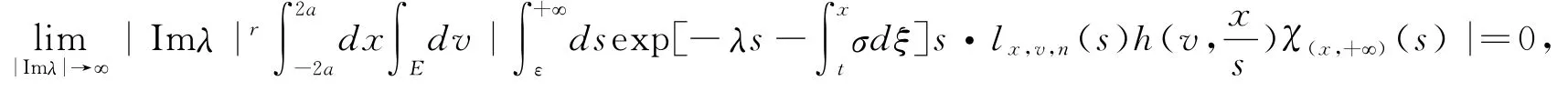
在Γ0成立。对∀n∈N，x∈（－2a，2a）固定，v∈E固定，并假设（si）1≤i≤m是其支撑集上的一个划分，并且对∀i∈｛1，2，···，m－1｝，当s∈［si，si＋1）时，可得Gx，v（s）＝Gx，v（si），故

第二步：证明

在Γ0上成立。对n∈N＼｛0｝，因为不可交换，而且具有下面的形式：，又由于，故即证：

同时Γ0上成立。下面不妨设J1是秩一算子，所以（2.4）式转化为证：

在Γ0内成立。设φ∈X，可得

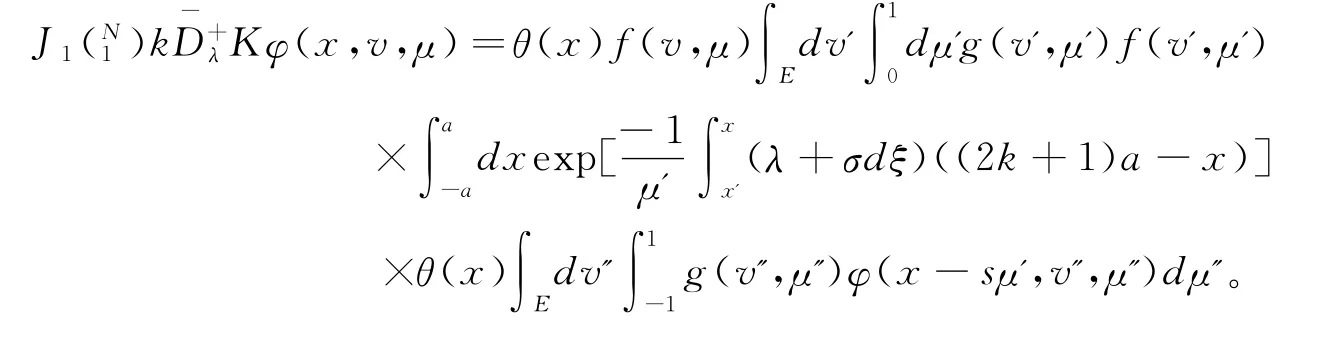
定义如下算子：

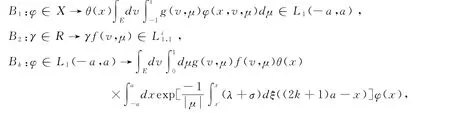
，由于

在Γ0上成立。又假设φ∈L1（（－a，a）；dx），是φ在R上的平凡拓展，于是根据Young不等式，可得：｜Bkφ｜≤｜Fλ｜｜L∞（R）｜｜φ｜｜L1（－a，a）。从而有

得到（2.4）在Γ0上成立。下证（2.5）式成立。由于J1紧算子，则只需证：对任意的r∈［0，1），

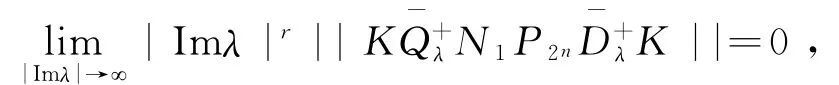
在Γ0上成立。事实上，对φ∈X，令，其中

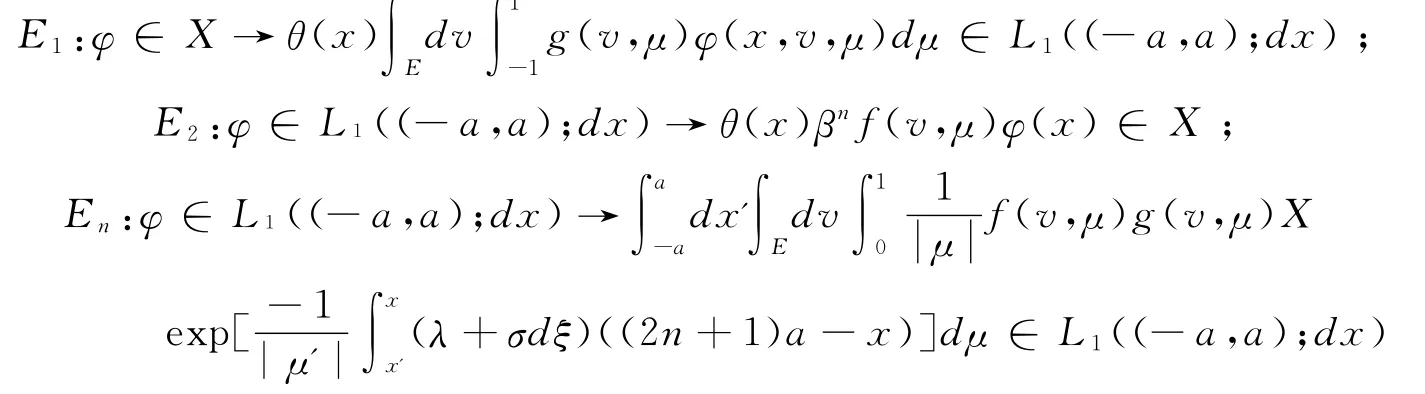
显然E1，E2与λ无关，类似（2.6）式的证明，故（2.3）式成立。

第三步：证明

在Γ0上成立，又由于

故要证（2.7）式在Γ0上成立，即证（2.2）、（2.3）和

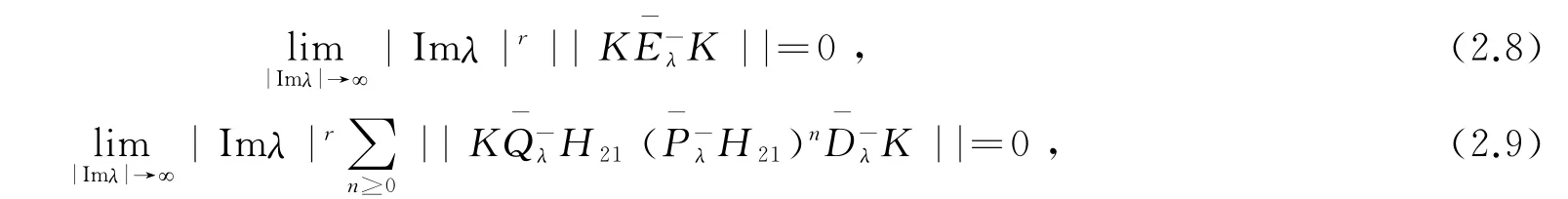
同时在Γ0上成立。由于（2.8）、（2.2）、（2.9）和（2.3）式具有完全相同的结构，故同理可证明（2.8）、（2.9）式在Γ0上成立。故（2.7）在Γ0上成立。

第四步：证（2.1）式在Γ0上成立。显然｜｜K（λI－B）－1K｜｜≤｜｜K（λI－）－1K｜｜，由第三步的证明可以得到在Γ0上成立。

令P（A）＝σ（A）∩Γ0是迁移算子A的谱点集。

定理2.2 若假设（O1）、（O2）被满足，对任意的t＞0，则R9（t）是X上的弱紧算子，并且P（A）仅由有限个具有限代数重数的离散本征值组成。

证明 显然，对任意的Reλ＞λ0，可得（λI－B）－1K是X上的弱紧算子，因为（λI－B）－1在Γ0上有界，故（λI－B）－1［K（λI－B）－1］m是X上的弱紧算子。

令W（λ）＝（λI－B）－1［K（λI－B）－1］4，又由于，所以

［1］Lehner J，Wing G M.On the spectrum of an unsymmetric operator arising in the transport theory of neutron［J］.Communications on Pure and Applied Mathematics，1955，8：217－234.

［2］Latrach K，Dehici A.Spectral properties and time asymptotic behaviour of linear transport equations in slab geometry［J］.Mathematical Methods in the Applied Sciences，2001，24：689－711.

［3］王胜华，贾善德.板几何中一类具周期边界条件迁移算子的谱［J］.西南师范大学学报，2005，30（6）：964－970.

［4］王胜华，吴红星.板几何中具反射边界条件的迁移算子的谱分析［J］.数学的实践与认识，2008，38（22）：197－203.

［5］Latrach K，Megdiche H.Time asymptotic behavior for Rotenberg’s model with Maxwell boundary conditions［J］.Discerte and continuous dynamical systems，2011，29：305－321.

［6］Latrach K，Megdiche H，Taoudi M A.Compactness properties for perturbed semigroups in Banach spaces and application to a transport model［J］.Journal of Mathematical analysis applications.，2009，359：88–94.

［7］王胜华，黄伟.板几何中一类具抽象边界条件迁移算子的谱［J］.应用泛函分析学报，2011，13（3）：267－273.

［8］吴红星，王胜华.板几何中具广义边界条件的迁移算子的谱［J］.南昌大学学报（理科版），2009，33（5）：415－420.

［9］Amar A B，Jeribi A，Mnif M.Some applications of the regularity and irreducibility on transport theory［J］.Acta applicandae mathematicae，2010，110：431－448.

［10］Mokhtar－Kharroubi M.Time asymptotic behaviour an compactness in neutron transport theory［J］.European Journal of Mechanics B Fluids，1992，11：39－68.

Compactness and Regularity of Applications to Transport Equations

WU Hong－xing1，YE Gui－ying2，CHENG Guo－fei1

（1.School of Mathematics and Computer Science，Shangrao Normal University，Shangrao Jiangxi 334001，China；2.Third Primary Schools in Shangrao County，Shangrao Jiangxi 334101，China）

The objective of this paper is to research the transport equation of continuous energy and inhomogeneous medium with abstract boundary conditions in L1space.It is to prove that the transport operator generates C0semigroup and the remained termR9（t）of the Dyson－Phillips expansion of the semigroup is weakly compact in L1space with the boundary operator being partly compact and disturbance operator is regular，and it obtains that the spectrum of the transport operator only consists of finite isolated eigenvalues with finite algebraic multiplicity.The main metheods rely on the theory of linear operators，resolvent and comparison operator.

boundary condition；compactness；transport equation；regularity；discrete eigenvalues

O177.2

A

1004－2237（2016）03－0001－05

10.3969／j.issn.1004－2237.2016.03.001

2016－04－07

国家自然科学基金（11461055）；江西省自然科学基金（20151BAB201029）和江西省教育厅科技项目（151056）

吴红星（1980－），男，江西余干人，副教授，硕士，主要从事迁移方程研究。E－mail：jxsruwhx＠163.com