摩擦摆隔震支座力学模型的探讨
2016-08-02龚健
龚健
(广东省建筑设计研究院,广州 510010)
摩擦摆隔震支座力学模型的探讨
龚健
(广东省建筑设计研究院,广州 510010)
建立了与双线性模型、Bouc-Wen模型以及FP模型相对应的两节点连接单元,模拟FPB在低周反复加载下的滞回特性,比较了3个模型分析结果的异同;最后,通过对FP模型进行参数影响分析,探讨了3个力学模型的适用范围。研究结果表明:在库伦摩擦假定及支座轴力不发生变化的前提下,3个模型所得滞回曲线较为一致,用以模拟FPB均是可行的;FP模型能考虑高速与低速摩擦系数不同,且能考虑动轴力的影响,故该模型更能贴近FPB真实的工作性态,更具广泛适用性,建议优先采用。
摩擦摆隔震支座;力学模型;低周反复;滞回特性;摩擦系数
1 引言
摩擦摆隔震支座/系统(FPB/FPS)除了具有平面滑移隔震装置的对地震激励频率范围低敏感性和高稳定性外,其特有的圆弧滑动面还具有一定的自复位功能,使其在实际应用中更为简便,因而受到了各国学者的广泛关注和深入研究,取得了大量研究成果,而且在不少新建及加固改造工程中,得到应用[1,2]。在研究和应用中,最为关键的技术问题之一是计算模型的选取和参数的确立。本文首先对FPB做了简化理论分析,随后选取了双线性等3种力学模型,分别建立对应的两节点连接单元进行低周反复加载模拟滞回特性并做参数影响分析,最后对比优缺点给出了模型选取建议。
2 摩擦摆隔震支座工作原理和简化理论计算
摩擦摆隔震支座工作原理是:在滑动过程中通过聚四氟乙烯等低摩擦材料的摩擦和摆动并附加阻尼给结构,从而耗散地震能量。摩擦摆隔震系统可简化为一个沿圆弧滑道运动的滑块,通过列力学平衡方程可求解支座的水平力F,限于篇幅,在此仅给出结果[3],F可表示成“回复力”和“摩擦力”之和,
即:

当θ很小时,式(1)可简化为:

式中,R为滑道及滑块底部圆弧面半径;W为滑块承载质量;D为位移;摩擦力f=μW,μ为摩擦系数;θ为滑块相对于滑道竖向对称轴的转角。由式(2)以及支座刚度的各向对称性,可以将其力学模型近似取为双线性模型,如图1所示。

图1 摩擦摆隔震支座的滞回模型
图中,Ki为初始刚度,Ki=μW/Dy;Dy为屈服位移;Kfps为支座的摆动刚度,Kfps=W/R;Keff为等效刚度;Dd为支座的设计位移。
3 摩擦摆隔震支座力学模型
为了避免单元过多而引起的耗时费力,在工程结构整体的分析中,常采用可表达支座恢复力模型的连接单元进行简化替代。鉴于Bouc-Wen模型在一定条件下表现出与双线性一致的特征且为FP模型的演变基础,本文接下来分别采用SeismoStruct中的对称双线性Bl-sym单元、SAP2000中的Plastic(Wen)和Friction Isolator单元,建立双线性、Bouc-Wen以及可考虑动轴力和双方向耦合的FP模型对FPB进行拟合,并通过相关影响参数分析研究了三者的差异及其适用性。
4 两节点单元模型的建立及滞回分析
假定摩擦摆隔震支座参数为:摩擦系数μ=0.1;球面半径R=1.5m;设计位移Dd=0.15m;屈服位移Dv=0.00254m,竖向荷载500kN。对3个模型进行了低周反复加载,对比支座的滞回性能。
4.1 Bl-sym
在SeismoStruct中,将X,Y剪切向采用对称双线性模型,如图2所示。按支座参数计算,分别定义初始刚度19 685 039N/m、屈服强度50000N和屈服后刚度比0.016933;其他方向采用线性并忽略该方向变形。模型按正弦波于顶部节点施加X向位移,频率为0.5Hz,加载2圈,幅值分别为1/2倍和1倍设计位移,即75mm和150mm。
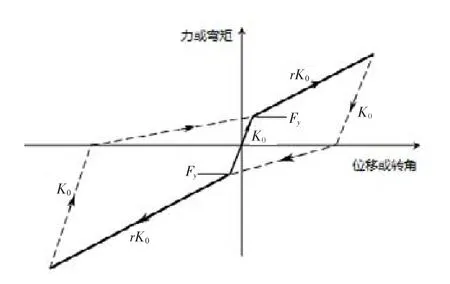
图2 双线性和线性模型
4.2 Pl ast i c(W en)
在SAP2000中建立了代表Bouc-Wen模型的 Plastic(Wen)连接单元,参数如表1所示。对模型进行非线性时程分析,加载采用位移加载,同前所述。

表1 Bouc-W en模型参数
4.3 Fri ct i on Isol at or
在SAP2000中,建立代表FP模型的Friction Isolator单元,模型参数如表2所示。FP模型须施加竖向荷载并定义竖向属性,在此将竖向刚度设为105倍水平向刚度,即认为竖向变形很小,可忽略不计。摩擦系数随速度变化比率的控制参数在此取为30s/m[4]。约束条件和加载历程同前,在此不赘述。

表2 Fri ct i on Isol at or模型参数
4.4 分析结果对比

图3 摩擦摆隔震支座滞回曲线图
通过对以上3种连接单元进行低周反复作用,考察各模型所得滞回性能,并与简化理论分析对比,检验各模型的合理性,对比结果如图3所示。
由图3可知,依照3种模型建立的3个连接单元模型所得滞回曲线极其吻合,与简化理论分析稍有差别,是因为理论分析中假定初始刚度无穷大。
5 影响参数分析
在上述分析中,FP模型也采用库伦摩擦假定,但高速和低速时摩擦系数存在差异[5,6]。因此,为了揭示该模型中的各参数的影响规律,以下将对FP模型进行参数分析,对加载速度、频率以及控制摩擦系数与滑动速度关系的比率参数进行了探讨。各分析工况如表3所示,其余模型参数同表2。各工况滞回曲线对比如图4所示。

表3 分析工况
从图4a可知,由于加载两周的幅值分别为75mm和150mm,而频率为0.5Hz,速度非常快。因此,在该分析中μmax起关键作用,大的则滞回圈明显更大;图4b更为清晰地反映了摩擦系数随加载速度(频率)增大而增大的现象,工况4~工况6相等位移下支座水平力明显在增大。即使在同一个工况中,由于第二圈比第一圈的位移幅值大,即该圈的速度要大,所表现出来的摩擦系数或屈服力也更大;而工况6~工况8由于都处于高速状态,因此摩擦系数基本达到μmax=0.15的稳定状态,故相差不大,各工况的屈服力分别达到72.04kN,74.96kN和75kN。从图4c可发现该摩擦系数-速度比率控制参数对支座的滞回曲线影响不是很大(当取值在15~30s/m范围内时),在支座位移变向时,此处主要表现为位移到达加载该圈的位移峰值处的曲线光滑程度。当比率参数越小时,转角处更光滑,当比率参数越大时,转角处更尖锐,更趋近于双线性模型。
在摩擦摆隔震支座的实际工作中,摩擦系数在高速和低速时确有不同,但在二者相差不大的情况下,如本例中的工况6~工况8,可采用双线性和Bouc-Wen模型进行模拟。地震作用下FPB的工作性态较为复杂[7],因此,如需考虑摩擦系数随速度变化以及轴力的变化,则应采用FP模型。
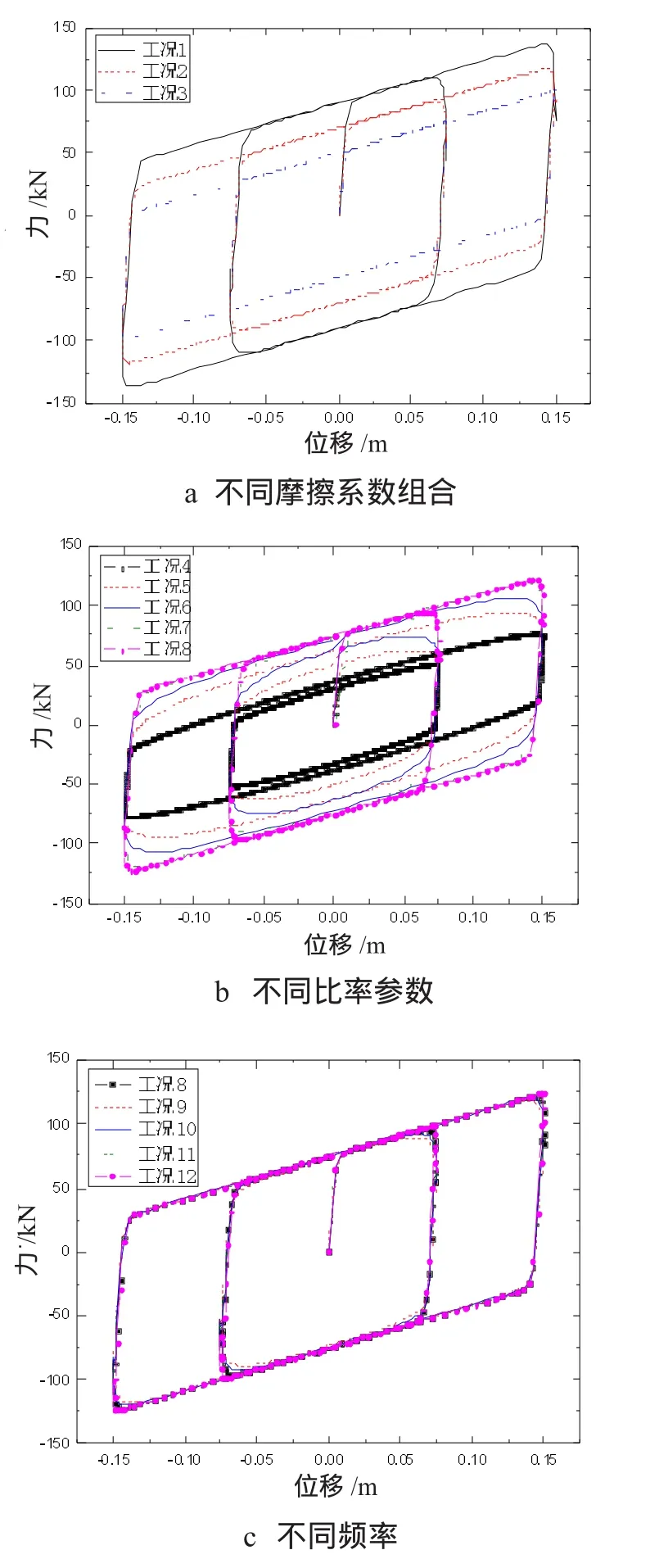
图4 各分析工况下的滞回曲线对比图
6 结论
本文介绍了FPB模型,在SeismoStruct和SAP2000中,分别建立了相对应的两节点连接单元并模拟其滞回性能,同时通过对FP模型的影响参数分析讨论了各模型的优缺点及适用范围。综上所述,可得出以下结论:1)在库伦摩擦假定及支座轴力不发生变化时,用双线性模型、Bouc-Wen模型和FP模型来模拟FPB在一定程度上均是可行的。
2)采用双线性模型和Bouc-Wen模型模拟FPB是有一定局限性的,它无法考虑高速与低速摩擦系数的不同,以及动轴力的影响。相比之下,FP模型更能反映FPB真实的工作性态,具有广泛适用性,建议在摩擦摆隔震结构分析中优先采用。
【1】龚健,周云.摩擦摆隔震技术研究和应用的回顾与前瞻(I)——摩擦摆震支座的类型与性能[J].工程抗震与加固改造,2010,32(3):1-10.
【2】周云,龚健.摩擦摆隔震技术研究和应用的回顾与前瞻(II)—摩擦摆隔震结构的性能分析及摩擦摆隔震技术的应用[J].工程抗震与加固改造,2010,32(4):1-19.
【3】龚健.新型摩擦摆隔震支座及其隔震结构体系研究[D].广州:广州大学,2010
【4】王建强,管品武,李大望.摩擦摆基础隔震结构双向地震反应分析[J].世界地震工程,2005,21(3):11-15.
【5】ConstantinouM.C,MokhaA.,ReinhornA.M.Teflonbearingsinbase isolation II:Modeling[J].J.StructuralEngineering,ASCE,1990,116 (2):455-474.
【6】MokhaA,ConstantinouM C,ReinhornAM.Furtherresultson frictional propertiesofTeflonbearings[J].J.StructuralEngineering, 1991,117(2):622-626.
【7】龚健,周云,邓雪松.某摩擦摆隔震框架结构地震反应分析[J].土木工程学报,2012,45(S2):146-150.
Discussion on the Mechanical Models of Friction Pendulum Bearing
GONG Jian
(TheArchitecturalDesign&Research InstituteofGuangdongProvince,Guangzhou510010,China)
Two-node linkelementsofbilinearmodel,Bouc-WenmodelaswellastheFPmodelareestablished,hystereticpropertyofFPB issimulatedby loadingon low cyclic loads,thesimilaritiesand differencesbetween theanalysisresultsof those threemodelsarecompared. Finally,theapplicationscopeofthe threemechanicalmodelsisdiscussed through theparametersanalysisofFPmodel.Theresultsshow that: under theprem iseofcoulomb frictionassumptionandunchangedaxial force,thehysteretic loopsof thosemodelsarevery consistentso that they'reall feasible tosimulateFPB inacertainextent;thedifferentfriction coefficientsunderhighand low speed,and theimpactofdynamic axialforcecanbothbeconsidered in FPmodel,which ismorecloseto therealbehaviorofFPBby contrast,therefore,FPmodelissuggested to beadopted inpreferencebecauseofitsgeneralapplicability.
frictionpendulum bearing;mechanicalmodel;low cyclic loads;hystereticproperty;frictioncoefficient
TU352.12
A
1007-9467(2016)08-0038-03
10.13616/j.cnki.gcjsysj.2016.08.004
2016-03-15
龚健(1987~),男,江西吉水人,工程师,从事结构抗震抗风与加固研究,(电子信箱)gongjian_07@163.com。
