行车速度对半敞开式公路隧道自然通风的影响

巢万里，李冬霞

(1.湖南省交通科学研究院，湖南 长沙 410015；2.山西省交通职业技术学院，山西 太原 030031)



行车速度对半敞开式公路隧道自然通风的影响

巢万里1，李冬霞2

(1.湖南省交通科学研究院，湖南 长沙 410015；2.山西省交通职业技术学院，山西 太原 030031)

摘要:采用ANSYS中的FLUENT版块，综合考虑隧道长度和通风口面积等影响因素，在通风段布置方式相同的情况下，通过改变行车速度的快慢，进行多次对比计算，研究分析隧道静压、动压及风速的变化情况。研究结果表明：随着行车速度的增加，隧道内流场静压动压和风速等极值增大，且波动幅度增大；随着行车速度的增加，行驶车辆的影响范围逐渐增大。尤其当车辆行驶在通风段中时，通风口之间的对流作用随着车辆行驶速度的增加逐渐加大，对流场的影响范围也显著增加；在通风段布置相同时，随着行车速度的增加，自然通风效果变好。当车速大于30 km/h时，隧道内的静压、动压和风速均出现大幅度的变化，满足自然通风的要求；当行车速度小于30 km/h时候，需要进行局部机械通风。

关键词：自然通风；半敞开式城市隧道；行车速度；静压；动压

行驶在隧道内的车辆具有一定的速度和断面积，会造成隧道内尤其是车体周围空气的流动，这种由车辆运动所引起的隧道气流运动产生的交通通风力为“活塞风”。当沿隧道前进方向的上方(或侧壁)间断设有通风孔与外界大气连通时,隧道内部的气流运动必将在通风孔产生相应的压力,使得通风孔产生排出或吸入气流[1-2]。对于车流量较大、车速较高的单向隧道，由车流运动所产生的交通风压是自然通风的主要动力[3-4]。国内外学者已经对自然通风隧道开展了相关研究。童艳等[5]利用理论分析和实验研究的方法，建立了全长隧道污染物分布模型，在此基础上得到了不同竖井间距、竖井截面、车速和主体长度下，隧道内污染物浓度的分布情况，指出提高车速和降低主体长度能有效改善污染物的分布情况。钟星灿等[6]将公路隧道内随机运动的车流假定为恒定持续的车流,根据动量、能量和质量守恒的基本定律,建立相关的关系式,探索分析这种隧道自然通风的气流运动规律，得出了在有条件设置通风孔的前提下,单向公路交通隧道采用这种自然通风方式是一种有效的通风方案。任韧[7]采用CFD软件对隧道内的交通活塞风进行了数值模拟，讨论了活塞风对隧道内空气速度场和压力场分布的影响，以及2辆汽车错车前后隧道内的流场分布。但是鲜有将隧道长度、通风口面积等因素综合考虑来分析不同行车速度对隧道自然通风的影响的研究。在此，本文通过ANSYS中的FLUENT版块进行二维模拟计算分析，综合考虑隧道长度、通风口面积等影响因素下，研究行车道速度对半敞开式隧道自然通风的影响规律。

1城市隧道自然通风理论

城市自然通风隧道，车辆行驶引起的气流运动以及外界大气是影响隧道内气体流动的主要因素，作用在隧道内气流上的作用包括：交通通风力、交通阻抗力(包括局部阻力、沿程阻力)[8-10]。

1.1交通通风力

单向交通的交通通风力可按下式计算：

(1)

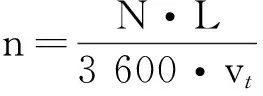
汽车等效阻抗面积可按下式计算：

(2)

式中：Acs为小型车正面投影面积，m2；ξcs为小型车空气阻力系数；Acl为大型车正面投影面积，m2；ξcl为大型车空气阻力系数；rl为大型车比例。

2.2交通阻抗力

交通阻抗力主要包括局部阻力和沿程摩擦阻力。局部阻力和沿程摩擦阻力分别是由隧道进出口、通风孔及隧道壁面摩擦所产生的阻力。

(3)

(4)

根据《隧道通风设计细则》(JTJ/TD70/2—02—2014)第7.1.4条, 本文的风与隧道隧道沿程阻力系数λ取0.02，隧道局部阻力系数ξ取1.0。

2隧道模型的建立

本文模型的建立是依据湖南省拟建京港澳国家高速公路长沙连接线中的矩形双向城市隧道马栏山隧道进行的模拟计算。该隧道U型槽段长619m，地下封闭段长约1 050m，通风口的高度为2.8m，隧道纵断面高度为5.2m。

依托该隧道进行模拟计算，并将模拟隧道的范围扩展到2 500m，模拟隧道长度分别为1 000，1 500，2 000和2 500m。

自然风速：2.67m/s；速度入口处湍流强度：0.05；湍流黏性比：0.1；网格尺寸：0.25m。

车辆进入隧道后匀速前进，在隧道内行进过程中不考虑车辆加减速或停车等情况。车辆的尾部为质量入口，通风口顶部和隧道出口为出流。本文中只考虑CO的排放，其他气体不做研究。本文的计算模型主要考虑交通风压对隧道通风的影响，热压对隧道通风影响的有限，因此在本次模型计算中暂不考虑[11-16]。

2.1几何建模

本文采用二维建模，隧道内通风口组即通风口均匀布置，共设置4个通风口组，因此将隧道全长进行分段，如图1所示，可见隧道共分为9段，若隧道全长为L，则：L=2L1+4L2+3L3，其中L1为缓冲段即隧道进口或者出口至最近通风口边缘的距离。L2为通风段即隧道纵向一个通风口组的长度，L3为相邻2个通风段之间的间隔。经试算，L1长度取为0.1L时，隧道通风效果较好，因此取L1=0.1L。

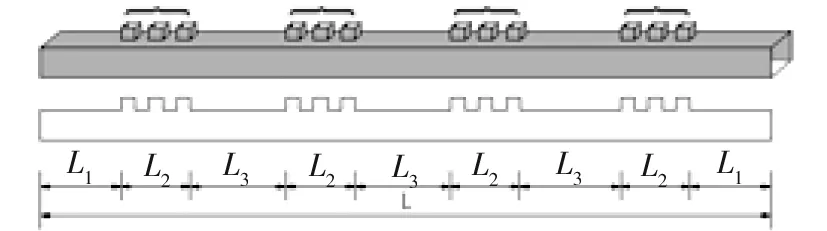
图1　隧道长度示意图Fig.1 Sketch map of the length of tunnel

一个通风段L2的布置见图2。本文模型中单个通风口的长度m=8。h为通风口的高度，m为单个通风口在隧道纵断面的长度，s为一个通风口组内相邻两个通风口之间净距，n为单个通风口的数量，L2=n×m+(n-1) ×s。经试算，在隧道长度为1 000m时，S取为16m时隧道通风效果最好，对于其余长度的隧道，S的距离为16×nm并取整，n为隧道长度的比值。最终试验模型各段长度见表1。

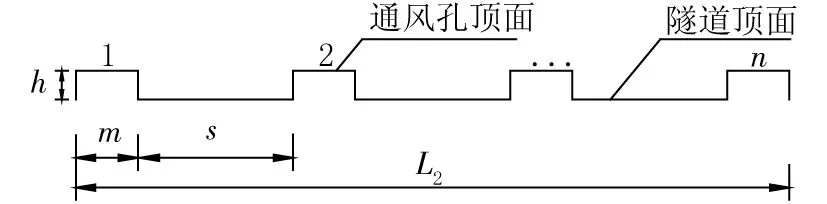
图2　通风段L2的布置示意图Fig.2 Sketch map of the arrangement of ventilation section L2

通过试算可以发现：行驶车辆驶出通风段进入间隔段并行驶一定距离之后对缓冲段和通风段的流场不产生任何影响，且对间隔段的影响也仅仅集中在车辆周边很小的区域内，因此在间隔段中截取L2′长度参与计算，并由试算得出一般情况下L2′长度与缓冲段L1长度相同即可。

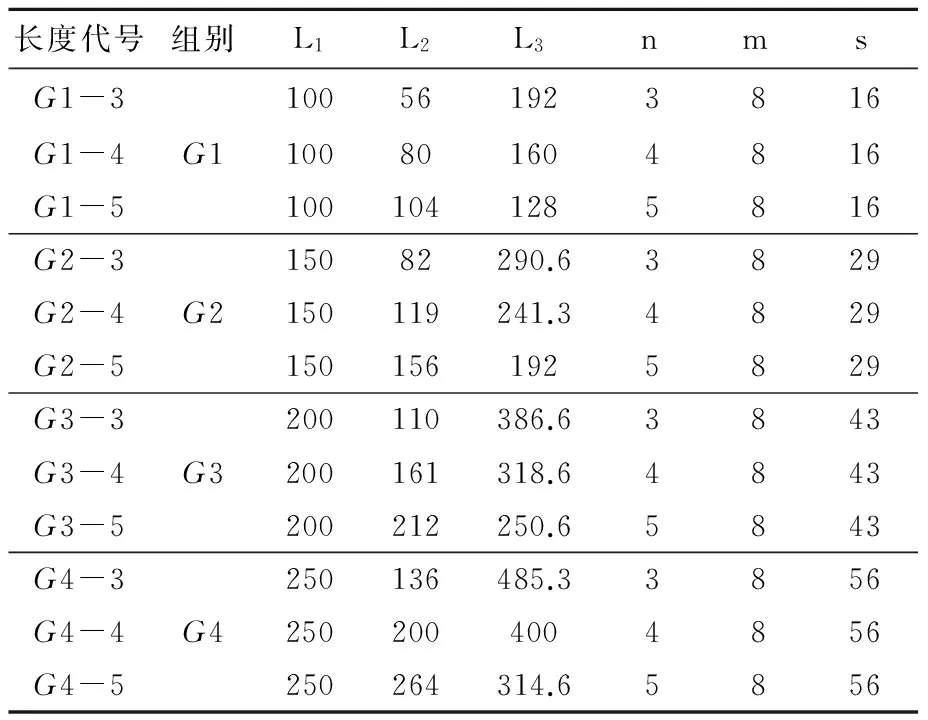
表1　试验模型各段长度Table 1 Length of each part of the final experimental model　m

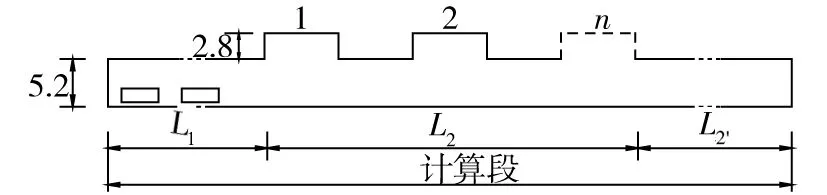
单位：m图3　计算段模型Fig.3 Model of calculation section

2.2对比试验

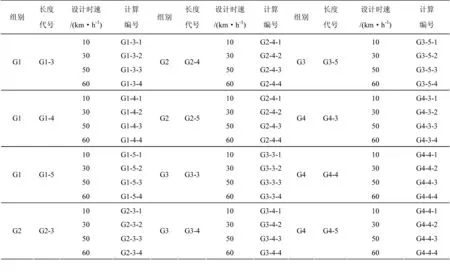
车辆匀速在隧道内行进中，行驶速度不同隧道内通风效果也不同。为了准确分析行车速度对通风效果的影响，选取同一组别、同一长度代号和不同计算编号的计算结果进行分析。若G3-5 内的G3-5-1，G3-5-2，G3-5-3和G3-5-4之间对比为1次分析，则共有12次对比分析,见表2。表中组别G1，G2，G3和G4分别代表隧道长度为1 000，1 500，2 000和2 500m。长度代号G1-n中的n代表通风口的个数。如G1-4-2表示在本次试验中隧道长度为1 000m，隧道1个通风口组有4个通风口，行车速度为30km/h。

1次对比分析中的4个计算模型仅有车辆行驶速度不同，其余完全相同：1)隧道长度相同；2)隧道内通风口布置方式相同：缓冲段、通风段和间隔段完全相同；3)计算长度相同：建模长度完全相同。由于数据量较大，本文仅选择G1-3组进行详细的分析说明。

2.3测点布置

为了方便比较，形象直观地显示计算所得，设置了多个典型测点，X即为隧道纵向(走向)，Y即为隧道高度方向。如图4所示。

表2对比试验

Table2Contrasttest

单位：m图4　测点布置图Fig.4 Observation points arrangement

由于车辆的在隧道内行驶的时刻不同在隧道内的位置不同，因此选择几个典型的时刻进行分析，各个时刻车辆的位置说明如表3所示。

表3　各个时刻车辆位置的说明

3计算结果及分析

3.1计算结果

由于计算数据较多，在此，仅列出测点1～测点3的计算结果。见图5～13所示。

3.2计算结果分析

静压计算结果分析:

1)G1-3-1即阻滞速度下，各个测点在各个时刻的静压变化较小，均在0值左右波动，即和大气压强值左右有微小的变动；

2)各个测点随着车辆行驶速度的增加，静压数据的波动范围逐渐增大，G1-3-4数据形成的折线图将其他折线图“包络”起来；

3)当行车速度大于30km/h时，静压出现明显变化，波动幅度较大。

动压计算结果分析:

1)同静压变化一致，G1-3-1各个测点在各个时刻的动压变化较小，均在0值左右波动，即G1-3-1中车辆产生的运动压强较小；

图5　测点1的静压Fig.5 Static pressure of observation point 1

图6　测点2的静压Fig.6 Static pressure of observation point 2

图7　测点3的静压Fig.7 Static pressure of observation point 3

图8　测点1的动压Fig.8 Dynamic pressure of observation point 1

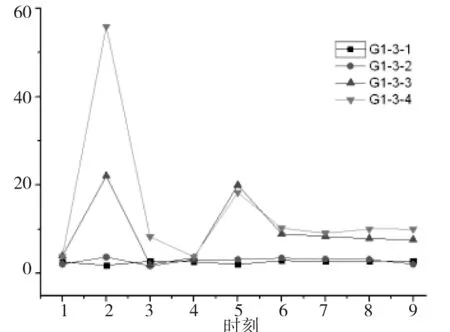
图9　测点2的动压Fig.9 Dynamic pressure of observation point 2

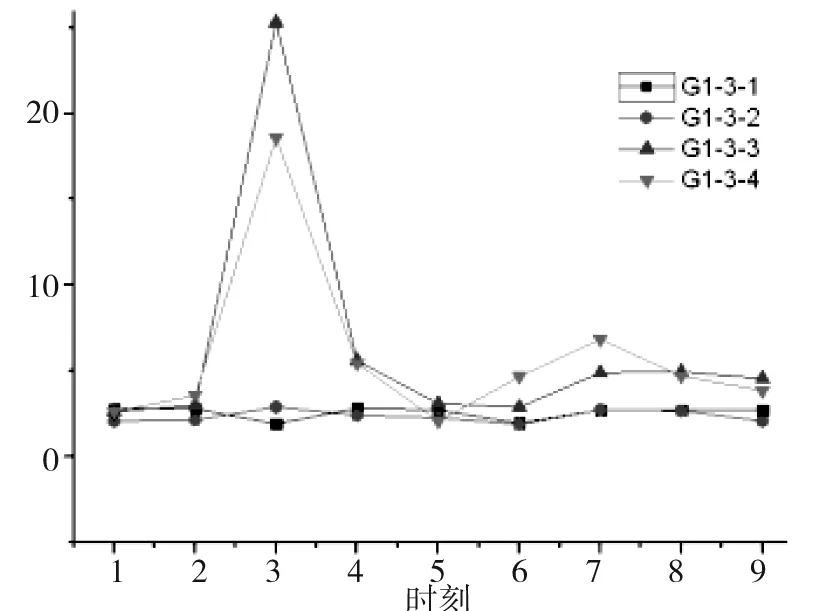
图10　测点3的动压Fig.10 Dynamic pressure of observation point 3

2)从测点1-～测点9的动压变化图可以看出各个速度下，测点1在时刻1，测点2在时刻2，测点3在时刻3，测点4在时刻4，测点5在时刻5，测点6在时刻6，测点7在时刻7，测点8在时刻8，测点9在时刻9时的动压数据为极值；

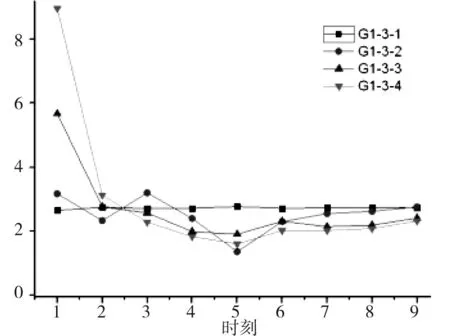
图11　测点1的风速Fig.11 Wind velocity of observation point 1

图12　测点2的风速Fig.12 Wind velocity of observation point 2

图13　测点3的风速Fig.13 Wind velocity of observation point 3

3)测点1～测点18，随着车辆行驶速度的增加，动压数据的波动范围逐渐增大，G1-3-4数据形成的折线图将其他折线图“包络”起来；

4)测点19～测点21，G1-3-1，G1-3-2，G1-3-4的动压波动范围较小，动压数值几乎重合，而G1-3-3动压波动范围最大，形成包络趋势；

5)当行车速度大于30km/h时，动压出现明显变化，波动幅度较大。

风速计算结果分析：

1)同动压变化一致，G1-3-1各个测点在各个时刻的风速变化较小；

2)从测点1-～测点9的风速变化图可以看出：各个行驶速度下，测点1在时刻1，测点2在时刻2，测点3在时刻3，测点4在时刻4，测点5在时刻5，测点6在时刻6，测点7在时刻7，测点8在时刻8，测点9在时刻9时的风速数均为极值；

3)随着车辆行驶速度的增加，风速数据的波动范围逐渐增大，G1-3-4数据形成的折线图将其他折线图“包络” 起来。仅有测点13和测点15分别由G1-3-2和G1-3-3形成的折线图包络；

4)当行车速度大于30km/h时，风速出现明显变化，波动幅度较大。

同理按照G1对比分析中的分析方法，完成了G2～G4各组的分析，与上述结果基本相似。

4结论

1)随着行车速度的增加，隧道内流场静压动压和风速等极值增大，且波动幅度增大；

2)随着行车速度的增加，行驶车辆的影响范围逐渐增大。尤其当车辆行驶在通风段中时，通风口之间的对流作用随着车辆行驶速度的增加逐渐加大，对流场的影响范围也显著增加；

3)在通风段布置相同时，随着行车速度的增加，自然通风效果越好。当车速大于30km/h时，隧道内的静压、动压、风速均出现大幅度的变化，满足自然通风的要求；当行车速度小于30km/h时候，需要进行局部机械通风。

参考文献：

[1] 李冬霞 半敞开式城市隧道通风口均匀布置方案研究 [D].长沙：中南大学，2014.

LIDongxia.Studyonprogramsofsemi-opencitytunnelwithventsevenlyarranged[D].Changsha:CentralSouthUniversity, 2014.

[2] 葛佳美.城市隧道顶部开孔自然通风研究[D].成都:西南交通大学,2010.

GEJiamei.Studyonnaturalventilationofurbantunnelwithuppervents[D].Chengdu:SouthwestJiaotongUniversity, 2010.

[3] 胡春艳.市政公路隧道顶部开孔自然通风研究[D].成都:西南交通大学,2007.

HUChunyan.Studyonnaturalventilationofurbantunnelwithuppervents[D].Chengdu:SouthwestJiaotongUniversity, 2012.

[4] 周湘川,赵望达,倪天晓. 顶隔板对公路隧道火灾烟气蔓延及温度的影响研究[J]. 铁道科学与工程学报,2011, 8(1):77-81.

ZHOUXiangchuan,ZHAOWangda,NITianxiao.Theinfluenceofroofspaceronthesmokespreadandtemperatureinhighwaytunnelfire[J].JournalofRailwayScienceandEngineering, 2011, 8(1):77-81.

[5] 童艳,苏荣华,龚延风.竖井型自然通风公路隧道气流与污染物分布的影响因素研究[J].建筑科学,2011, 27(6):92-98.

TONGYan,SURonghua,GONGYanfeng.Studyoninfluencefactorsaboutairflowandpollutiondistributionforroadtunnelsforwithshaftsundernaturalventilationcondition[J].BuildingScience, 2011, 27(6):92-98.

[6] 钟星灿，曾臻.自然通风公路隧道有害气体浓度分布[J].铁道工程学报，2006(9)：44-49.

ZHONGXingcan,ZENGZhen.Distributionofharmfulgasconcentrationinhighwaytunnelwithnaturalventilation[J].JournalofRailwayEngineeringSociety,2006(9):44-49.

[7] 任韧.对公路隧道交通活塞风的数值模拟研究[D].西安:长安大学,2012.

RENRen.Numericalsimulationresearchonthepistoneffectofvehicleinhighwaytunnel[D].Xi’an:Chang’anUniversity, 2012.

[8] 史力生,彭立敏.公路隧道纵向通风分析与计算[J].长沙铁道学院学报,1997,15(2):100-105.

SHILisheng,PENGLimin.Analysisandcalculationofthelongitudinalventilationintheroadtunnel[J].JournalofChangshaRailwayUniversity, 1997,15(2):100-105.

[9]廖仕超,王薇,徐志胜.基于证据理论的长大隧道火灾风险评价模型[J]. 铁道科学与工程学报,2010, 7(6):80-85.

LIAOShichao,WANGWei,XUZhisheng.Fireriskassessmentmodelbasedonevidencetheoryforlong-highwaytunnel[J].JournalofRailwayScienceandEngineering, 2010, 7(6):80-85.

[10] 彭帆.公路长隧道通风计算分析[J].公路工程, 2008,33(3):88-90.

PENGFan.Analysisandcalculationofventilationoflonghighwaytunnel[J].HighwayEngineering, 2008,33(3): 88-90.

[11]HirschCh.Numericalcomputationofinternalandexternalflows[M].NewYork:JohnWileyandSons,1988.

[12] 金学易,陈文英.隧道通风及隧道空气动力学[M].北京:中国铁道出版社,1983: 71-79.

JINXueyi,CHENWenying.Tunnelventilationandtunnelaerodynamics[M].Beijing:ChinaRailwayPublishingHouse, 1983: 71-79.

[13] 赵望达,李洪,徐志胜,等.基于因次分析的隧道火灾临界风速研究[J].铁道科学与工程学报,2009,6(6): 18-21.

ZHAOWangda,LIHong,XUZhisheng,etal.Tunnelfirecriticalventilationvelocitybasedondimensionalanalysis[J].JournalofRailwayScienceandEngineering, 2009, 6(6):18-21.

[14]AxelBring,Tor-GoranMalmstrom,CarlAlexBoman.Simulationandmeasure-mentofroadtunnelventilation[J].TunnellingandUndergroundSpaceTechnology, 1997,12 (3):417-424.

[15]SpaldingDB.Mathematicsandcomputersinsimulation[M].Holland:NorthHolland,1981.

[16]NoeldeNevers.Airpollutioncontrolengineering[M]. 2ndEdition.Beijing:McGraw-Hill, 2000: 536- 539.

* 收稿日期：2015-09-23

基金项目：湖南省交通科技项目(201023)

通讯作者：巢万里(1978-)，男，湖南汨罗人，高级工程师，从事岩土与地下工程设计与科研工作；E-mail:379034986@qq.com

中图分类号：U453.5

文献标志码：A

文章编号：1672-7029(2016)06-1222-07

Influence of driving speed of semi-open city tunnel on natural ventilation

CHAO Wanli1，LI Dongxia2

(1.HunanCommunicationsResearchInstitute，Changsha410015，China；2.ShanxiTrafficVocationalandTechnicalCollege,Taiyuan030031,China)

Abstract：Considering influence factors such as length of tunnel and the area of vents, a two-dimensional numerical simulation is presented in this paper by using FLUENT section of ANSYS. In the case of the same ventilation section arrangement and the change of driving speed, multiple contrast calculations were performed to analyze the changes of static pressure, dynamic pressure and wind velocity. The calculated example showed: With the increase of driving speed，the maximum of dynamic pressure and wind velocity will increase，and So as the volatility. With the increase of driving speed，influence scope of driving vehicle increase at the sare tine. When vehicle located at ventilation section, convection which between vents increases with the increase of driving speed，as well as the influence scope of the flow distribution. In the case of the same ventilation section arrangement, natural ventilation is better with the increase of driving speed. When driving speed is greater than 30 km/h, static pressure, dynamic pressure and wind velocity change greatly so that the request of natural ventilation can be satisfied; When driving speed is less than 30 km/h, sectional mechanical ventilation is needed.

Key words：natural ventilation; semi-open city tunnel;driving speed; static pressure; dynamic pressure