ARMA模型在浅埋刚性管线变形预测的应用研究

王海涛，宋词，王凯

(1.大连交通大学 土木与安全工程学院，辽宁 大连 116023；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)



ARMA模型在浅埋刚性管线变形预测的应用研究

王海涛1，宋词1，王凯2

(1.大连交通大学 土木与安全工程学院，辽宁 大连 116023；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

摘要:为了研究隧道开挖对浅埋刚性管线的影响，基于平稳时间序列分析理论，通过对ARMA模型的识别与定阶以及参数的估计，建立管线变形监测数据处理与预测的时间序列ARMA模型。利用该模型对大连地铁1号线千山路站浅埋刚性管线的变形进行预测，并将预测数据与实测数据进行比较，结果表明：两者拟合程度很高，ARMA模型取得较好的拟合效果和预测精度。说明ARMA模型对管线变形监测数据处理与预测是十分有效和可靠的，可为隧道开挖过程中，施工人员做出决策提供技术参考。

关键词：地铁隧道；埋地管线；ARMA模型；变形预测

地铁隧道工程一般处于城市中心地带，由于地层中各种管线交错密集、分布复杂，隧道施工必然会对其安全造成不利影响，严重威胁地下管线的正常使用和安全。同时，供水、污水管线等可为工程带来大量地下水，影响工程周围岩土体的稳定，严重时可导致工程事故的发生[1-5]。地下管线是城市的生命线，是城市赖以生存与发展的“神经”和“血管”，工程建设必须保证其安全。施工前应对地下管线进行变形预测，以确定其所受影响程度，并采取必要的保护措施。国内外学者在城市地下工程施工对邻近埋地管线的影响研究方面做了很多工作，研究方法主要包括理论计算[6-7]、现场测试[8]、模型试验[9]和数值模拟[10-11]等。关于地铁隧道施工时地层沉降及管线变形预测研究，主要采用理论计算法和基于实测数据的实测数据分析法[12]。理论计算法主要有以Peck理论为代表而不断发展、完善、改进的经验理论法，以及以有限元法为主的数值预测法等。实测数据分析法是指利用数学方法对统计数据进行处理并做出预测。按照假设前提的不同，实测数据分析法又分为回归分析和时间序列分析两大类。时间序列法包括了灰色预测、指数平滑法和自回归移动平均模型等[13-15]。20世纪70年代，美国统计学家G.E.P.BOX和英国统计学家G.M.Jenkins提出自回归移动平均模型 (Auto-regressivemoving-averagemodel，简称ARMA模型，也称B-J方法)。它是一种精度较高的时序短期预测方法，其基本思想是：某些时间序列是依赖于时间t的一组随机变量，单个序列值具有不确定性，但整个序列的变化是有规律的，可以以数学模型进行描述。ARMA模型强调“让数据自己说话”，不需要事先假定数据存在着一定的结构或模式，而是从数据本身来寻找可以较好描述数据的模式，从而可以保证模型与数据拟合较好。该模型在预测过程中既考虑了研究对象在时间序列上的依存性，又考虑了随机波动的干扰性。与平稳时间序列、周期时间序列模型相比，ARMA模型的建模方法在数学上较为完善，预测的精度较高。本文通过对ARMA模型的识别与定阶以及参数的估计，建立管线变形监测数据处理与预测的时间序列ARMA模型。利用该模型对大连地铁1号线千山路站浅埋刚性管线的变形进行预测，为隧道开挖环境影响评价标准的建立提供理论参考。

1地铁隧道开挖对浅埋刚性管线的影响

地铁隧道开挖时地下管线与土体的相互作用主要表现为：管线对周围土体起约束作用，约束土体的变形，同时，土体对管线有反作用。在地铁隧道开挖之后，初期衬砌达到一定强度之前，围岩应力会发生调整进而产生变形甚至破坏。当围岩变形传递到管线处时，管线产生附加应力和弯矩，进而产生变形。由于管线对土体的锚固作用，土体变形得到一定的约束。管线与土体的相对刚度以及管线周围土体的变形决定了管线变形的大小。当管线轴线平行地铁开挖方向时，周围土体对管线起轴向拉压作用；当管线轴线垂直地铁开挖方向时，周围土体会增大管线接头转角和弯曲应力[16-17]。

1.1刚性管线

隧道开挖产生的地层变形会使刚性管线上产生弯矩，图1所示为采用焊接、法兰等刚性接口，材质较为坚硬的管线所受弯矩及与隧道的位置的关系。管线的弯矩及其抵抗地层变形的能力受接头位置、类型和刚度等的影响。

(a)管线与隧道垂直；(b) 管线与隧道平行图1　隧道开挖引起相邻管线附加弯矩特性图Fig.1 Additional moment characteristics graph of adjacent pipeline caused by tunnel excavation

1.2柔性管线

由若干节管道通过橡胶圈连接而成的承插接口管道(如球墨铸铁管、钢筋混凝土管等)，管材本身刚度较大且基本不产生变形，管线竖向变形主要由相邻接口处的相对转动来实现。当管线两端通过工作井、支墩等设施约束管线位移时，其稳定后中间段均匀沉降，竖向位移等于最大沉降量；其余不均匀沉降段呈折线状，总变形量逐渐增大。试验表明，对于敷设于同种土层中的管线而言，管线不均匀沉降段的相邻两节管道之间均存在一个大小相等的相对转角。通讯电缆等管线材质较为柔软时，则可随地层出现整体变形，变形及变化规律与地层较为一致。

刚性管线和柔性管线的控制标准并不相同，管线的埋深也影响着管线变形的直接测量，根据经验公式，可以将地表沉降值作为管线破坏的控制标准。浅埋刚性管线的控制标准为竖向沉降，由于埋深浅，沉降值可以直接测量。本文以浅埋刚性管线为例，介绍管线累计沉降值的预测方法，其他情形的预测方法及思路与此相同。

2ARMA模型

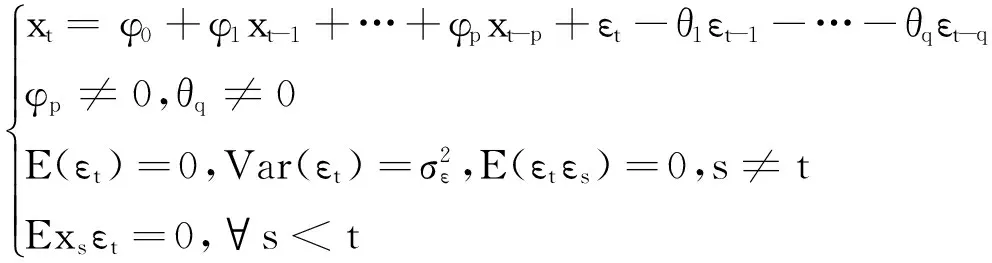
(1)

若φ0=0，该模型称为中心化ARMA(p,q)模型。缺省默认条件，中心化ARMA(p,q)模型可简写为：

xt=φ0+φ1xt-1+…+φpxt-p-θ1εt-1-…-θqεt-q

(2)

默认条件与AR模型、MA模型相同。引进延迟算子，ARMA(p,q)模型简写为：

Φ(B)xt=Θ(B)εt

(3)

式中：

Φ(B)=1-φ1B-…-φpBp，为p阶自回归系数多项式。

Θ(B)=1-θ1B-…-θqBq，为q阶移动平均系数多项式。

显然：当q=0时，ARMA(p,q)模型就退化成了AR(p)模型；当p=0时，ARMA(p,q)模型就退化成了MA(q)模型。所以，AR(p)模型和MA(q)模型实际上是ARMA(p,q)模型的特例，它们统称为ARMA模型。而ARMA(p,q)模型的统计性质也正是AR(p)模型和MA(q)模型统计性质的有机组合。

3基于ARMA模型的浅埋刚性管线变形预测

3.1工程概况及数据采集

大连地铁1号线工程千山路站地貌为冰碛丘陵，场地南高北低，地面高程34.49～38.38m。拟建车站附近建筑物密集，管线、管道众多。本区间范围内上覆第四系人工堆积层(Q4ml)、第四系中更新统冰碛层(Q2gl)、下伏震旦系五行山群甘井子组白云质灰岩(Zwhg)。本区间范围未发现明显的断裂构造，局部受区域构造影响，岩石节理裂隙较发育。场地构造稳定性总体较好。场地内无地表河流经过。千山路站J5527号铸铁管线，管径100mm，埋深0.8m。监测点埋设方法为：成孔深度严格控制在管线顶上方1.0m处，成孔直径φ200mm，然后进行人工掏土。当见管线顶部时，下放直径为φ40mm的钢管，然后在管线顶与钢管接触的部位灌注速凝混凝土，将管线顶部与钢管固结成一体，最后将高出路面的钢管截去。钻孔孔壁和钢管之间用细中砂回填。在孔口四周用砖砌成保护井，顶部为井盖和保护井圈。人工挖孔埋设沉降管回填材料为级配砂石，回填要分层振捣、分层回填、连续作业。必要时用竹竿、铁管、钢筋钎人工辅助插捣，以补充机械振捣不足。回填距离地面lm时，开始浇注混凝土至路面，为防止路面塌陷，雨水渗漏，浇注要密实，并在地面钢管处做保护井。其监测点的布置示意图如图2所示。现场测点实际埋设情况如图3所示。

图2　测点埋设示意图Fig.2 Sketch of measuring points

图3　现场测点埋设图Fig.3 Layout of monitoring point

管线累计沉降曲线如图4所示，管线日沉降量如图5所示。可以看出，地铁开挖导致管线产生沉降，开挖掌子面距离管线较近时管线日沉降量较大，日沉降最大值达0.46mm/d。

图4　管线累计沉降量随时间分布图Fig.4 Cumulative settlement of pipeline with time distribution

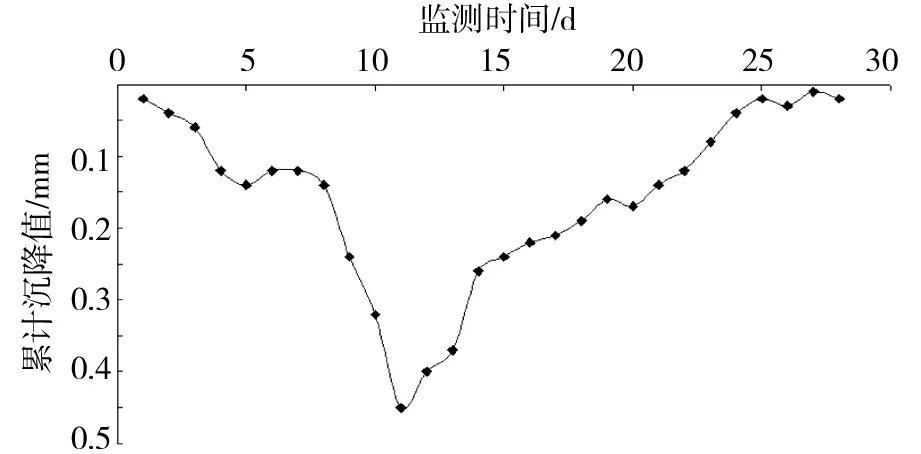
图5　管线日沉降量随时间分布图Fig.5 Day settlement of pipeline with time distribution

3.2数据平稳性检验

只有平稳序列才能直接建立ARMA模型。设累计沉降值序列为x，首先应检验x是否为平稳序列。可以通过序列的自相关系数检验序列的平稳性。自相关—偏自相关分析图如图6～7所示。

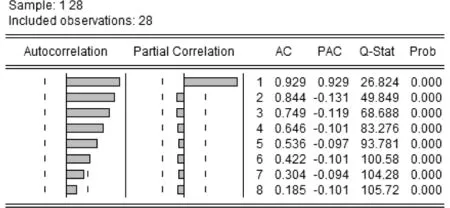
图6　x序列自相关—偏自相关分析图Fig.6 Analysis chart of x series autocorrelation-partial autocorrelation

图7　D(x)序列自相关—偏自相关分析图Fig.7 Analysis chart of D(x) series autocorrelation--partial autocorrelation

由图6可见，x序列的自相关系数并没有很快地落入随机区间，即不趋近于0。故x为非平稳序列。很多非平稳序列可以通过适当处理(比如，逐期差分)转化为平稳序列。对x序列进行二阶逐期差分，设新序列为x2，检验x2的平稳性。x2的自(偏)相关系数如图7所示，可见滞后期大于1时，自相关系数便落入随机区间，因此可以直观地判断x2为平稳序列。

为了更进一步判断x2的平稳性，比较x2样本均值与标准误差的大小关系，当样本均值落入正负2倍标准误差区间时，认为序列满足0均值假设，即序列满足平稳性。计算得到，x2的均值为-0.000 384，不显著为0的自相关系数取第1项，算得x2的标准误差为0.002 732。因此可以认为x2序列为平稳序列，可以建立ARMA模型。

3.3模型的识别与建立

观察图7，从自相关分析图可见，当滞后期大于1时，序列的样本自相关系数趋于0，从偏自相关分析，滞后3期以后的偏自相关系数明显不为0，并且序列的自相关函数和偏自相关函数都具有截尾性，因此可以建立ARMA(3,1)模型。

当p=3，q=1时，模型参数估计与相关检验结果如图8所示。从图8中可以看出：各滞后多项式的倒数根都在单位圆内，说明过程既是平稳的，也是可逆的。

因此，x2序列的表达式可以写成：

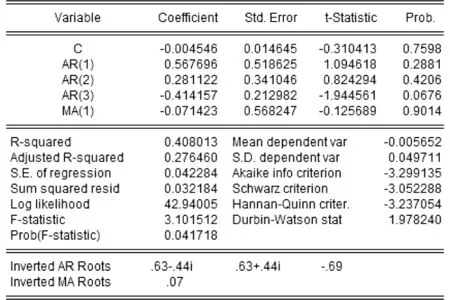
图8　模型参数估计与相关检验结果Fig.8 Model parameters estimation and related inspection result

3.4模型检验

常通过检验模型残差的随机性来评价模型的优劣。对x2序列建立ARMA(3,1)模型，对模型残差及残差平方进行自相关检验，结果如图9～10所示。可以看出，残差及残差平方的自相关系数很快地落入置信区间，从而可以直观地判断出残差序列是纯随机的。另外，用Jarque-Bera法检验残差的正态性，结果如图11所示，服从正态分布的概率为0.903 819。综上所述，模型的残差序列具有随机性，模型通过检验。

3.5管线变形预测

利用x2序列的ARMA(3,1)模型静态预测x序列，预测结果如表1所示。可以看出，两者拟合程度很高，前期数据预测误差相对较大，最大误差精度为8.0%，后期数据的预测精度相对较高，除个别数据有一定误差外，预测数据与原始数据基本重合。

图9　残差自相关—偏自相关分析图Fig.9 Analysis chart of residual error autocorrelation-partial autocorrelation

图10　残差平方自相关—偏自相关分析图Fig.10 Analysis chart of residual square autocorrelation--partial autocorrelation

图11　残差正态性检验Fig.11 Residual normality tests

利用ARMA模型，动态预测未来1个星期管线沉降累计值的变化情况，如表2所示。从表2可知，管线累计沉降量在4.47～4.50mm范围变化，变化幅度较小，即管线沉降已趋于稳定，可为施工人员做出决策提供技术参考。

表1　管线累计沉降预测结果及误差精度

表2　未来1个星期的预测值

4结论

1)基于ARMA模型对大连地铁1号线千山路站浅埋刚性管线的变形进行预测。通过对管线的累计沉降序列进行二阶差分得到序列x2，针对x2序列建立ARMA(3, 1)模型，并利用该模型预测了管线累计沉降，预测数据误差较小，除个别数据有一定误差外，预测数据与实测数据基本重合，表明ARMA模型可以用来预测管线累计沉降。

2)ARMA模型预测方法概念简单，结果反馈迅速，为隧道开挖环境影响评价标准的建立提供理论参考。

参考文献：

[1] 吴贤国，曾铁梅，张立茂,等.地铁施工邻近管线安全风险管理研究[J].铁道工程学报, 2013(9):127-132.

WUXianguo，ZENGTiemei，ZHANGLimao,etal.Researchonsafetymanagementofadjacentundergroundpipelinesinmetroconstruction[J].JournalofRailwayEngineeringSociety, 2013(9):127-132.

[2] 郭典塔，周翠英， 谢琳.近接地铁隧道基坑开挖静动力学行为研究[J]. 铁道科学与工程学报，2015,12(2): 393-401.

GUODianta,ZHOUCuiying,XIELin.Researchonstaticanddynamicperformanceofthefoundationpitexcavationadjacenttosubwaytunnels[J].JournalofRailwayScienceandEngineering, 2015,12(2): 393-401.

[3] 张成平, 张顶立, 王梦恕, 等.城市隧道施工诱发的地面塌陷灾变机制及其控制[J]. 岩土力学, 2010, 31(增1): 303-309.

ZHANGChengping,ZHANGDingli,WANGMengshu,etal.Catastrophemechanismandcontroltechnologyofgroundcollapseinducedbyurbantunneling[J].RockandSoilMechanics, 2010, 31(Suppl1): 303-309.

[4] 王凯.滨海地区钻爆法施工对邻近腐蚀管线的影响及风险评估分析[D]. 大连：大连理工大学, 2013.

WANGKai.Influenceofblastingexcavationonnearbycorrodedpipelineandriskassessmentincoastalareas[D].Dalian:DalianUniversityofTechnology, 2013.

[5] 王净伟, 杨信之, 阮波. 盾构隧道施工对既有建筑物基桩影响的数值模拟[J]. 铁道科学与工程学报，2014,11(4): 73-79.

WANGJingwei,YANGXinzhi,RUANBo.Numericalsimulationofshieldtunnelconstructionontheimpactofneighboringpilesfoundation[J].JournalofRailwayScienceandEngineering, 2014,11(4): 73-79.

[6] 段光杰. 地铁隧道施工扰动对地表沉降和管线变形影响的理论和方法研究[D].北京：中国地质大学, 2002.

DUANGuangjie.Thetheoreticalandmethodiealresearchonsurfacesettlementandpipelinedeformationduetoconstructiondisturbanceinmetrotunnelconstruction[D].Beijing:ChinaUniversityofGeosciences, 2002.

[7]VorsterT,KlarA,SogaK,etal.Estimatingtheeffectsoftunnelingonexistingpipelines[J].JournalofGeotechnicalandGeo-environmentalEngineering, 2005, 131(11): 1399-1410.

[8] 骆建军,张顶立,王梦恕, 等. 北京地铁暗挖车站施工对管线的影响分析[J]. 铁道学报,2007,29(5):34-38.

LUOJianjun,ZHANGDingli,WANGMengshu,etal.StudyontheinfluenceofstationsubsurfaceexcavationonundergroundpipelinesinBeijingMetro[J].JournaloftheChinaRailwaySociety,2007,29(5):34-38.

[9] 吴波, 高波, 索晓明, 等. 城市地铁隧道施工对管线的影响研究[J]. 岩土力学, 2004, 25(4): 657-662.

WUBo,GAOBo,SUOXiaoming,etal.Studyoninfluenceofmetrotunnelexcavationonburiedpipelines[J].RockandSoilMechanics, 2004, 25(4): 657-662.

[10]KlarA,MarshallAM.Shellversusbeamrepresentationofpipesintheevaluationoftunnelingeffectsonpipelines[J].TunnellingandUndergroundSpaceTechnology, 2007, 22: 1016-1022.

[11] 王霆, 刘维宁, 何海健. 地铁车站施工对邻近管线影响的三维数值模拟[J]. 北京交通大学学报, 2008, 32(1): 32-35.

WANGTing,LIUWeining,HEHaijian. 3DNumericalsimulationoneffectoftunnelconstructiononadjacentpipeline[J].JournalofBeijingJiaotongUniversity, 2008, 32(1): 32-35.

[12] 王铁生, 张利平, 华锡生.地铁隧道施工变形预测研究综述[J]. 水利水电科技进展，2003,23(5):62-65.

WANGTiesheng,ZHANGLiping,HUAXisheng.Reviewofpredictionofconstructiondeformationofmetrotunnel[J].AdvancesinScienceandTechnologyofWaterResources，2003,23(5):62-65.

[13] 邓聚龙. 灰预测与灰决策[M]. 武汉:华中科技大学出版社,2002.

DENGJulong.Greypredictionandgreydecision[M].Wuhan:HuazhongUniversityofScienceandTechnologyPress, 2002.

[14] 李世平, 郭泉河. 采用ARMA模型对变形监测数据处理与预报[J]. 矿山测量，2013(5): 70-72.

LIshiping,GUOQuanhe.UsingARMAmodelofdeformationmonitoringdataprocessingandprediction[J].MineSurveying, 2013(5):70-72.

[15] 尹光志, 岳顺, 钟焘, 等. 基于ARMA模型的隧道位移时间序列分析[J]. 岩土力学,2009,30(9):2727-2732.

YINGuangzhi,YUEShun,ZHONGTao,etal.TimeseriesanalysisoftunneldisplacementbasedonARMAmodel[J].RockandSoilMechanics,2009,30(9):2727-2732.

[16] 吴锋波, 金淮,尚彦军. 城市轨道交通隧道周边地下管线变形预测研究[J]. 岩石力学与工程学报,2013,32(增2):3592-3601.

WUFengbo，JINHuai，SHANGYanjun.Undergroundpipelinedeformationpredictionaroundurbanrailtransittunnelengineering[J].ChineseJournalofRockMechanicsandEngineering,2013,32(Suppl2):3592-3601.

[17] 向卫国，徐玉胜. 隧道施工扰动下管线变形三维预测方法及应用[J]. 地下空间与工程学报，2014,10(4): 920-925.

XIANGWeiguo，XUYusheng. 3Dsimulationpredictionmethodforpipelinedeflectionunderdisturbingoftunnelinganditsapplication[J].ChineseJournalofUndergroundSpaceandEngineering, 2014,10(4): 920-925.

* 收稿日期：2015-08-25

基金项目：国家自然科学基金资助项目(51208073)；辽宁省博士启动基金资助项目(20121061)

通讯作者：王海涛(1982-)，男，湖北随州人，副教授，博士，从事岩土工程与地下结构工程方面的研究;E-mail：wht@djtu.edu.cn

中图分类号：TU279.7

文献标志码：A

文章编号：1672-7029(2016)06-1122-07

Research on ARMA model and its application to prediction ofshallow buried rigid pipeline deformation

WANG Haitao1，SONG Ci1，WANG Kai2

(1.SchoolofCivilandSafetyEngineering,DalianJiaotongUniversity,Dalian116028,China;2.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China)

Abstract:In oder to study the effect of tunnel excavation on buried pipeline, the time series ARMA model for processing and forecasting the deformation data of pipeline. The stationary time series analysis theory, the estimation of parameters and the identification of the order of ARMA model is used in the process above. Using the method of time series to model and analysing the deformation monitoring data of shallow buried rigid pipeline in Qianshan Road Station of Dalian metro line one, the prediction are in good agreement with actual measurements; It is proved that the method is basically feasible.

Key words:subway tunnel; buried pipeline; ARMA model; deformation prediction