基于遗传算法的客运电力机车耐撞性优化设计

张凯，许平，姚曙光

(中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙 410075)



基于遗传算法的客运电力机车耐撞性优化设计

张凯，许平，姚曙光

(中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙 410075)

摘要:针对国内某新造客运电力机车，根据厂家实际需求，设计一组车辆端部吸能结构特性曲线，实现机车在25 km/h的碰撞速度下，有序而可控吸能，优化头部主吸能结构的变形长度。基于列车纵向多刚体碰撞动力学模型，构建以D1(头部主吸能结构的变形量)作为目标参数，x1(头部变形吸能元件塑变平台力)，x2(头部主吸能结构塑变平台力)和x3(重联端压溃管塑变平台力)为设计变量，d2(重联端压溃管行程)为约束条件的优化模型。采用遗传算法直接对优化模型进行整体寻优，得到端部吸能结构特性曲线的最优形式。研究结果表明：当x1=1.615 MN，x2=3.130 MN，x3=1.999 MN时，头车主吸能结构的变形长度可缩短至0.178 m，机车满足耐撞性要求，研究结果可用于指导机车的耐撞性设计。

关键词：客运电力机车；列车纵向动力学；耐撞性设计；优化；遗传算法

迄今为止，碰撞仍然是列车面临的主要事故风险之一，随着列车运行速度的不断提高，必然使得事故后果更加严重，因此开展轨道车辆的耐撞性研究，提高轨道交通工具的被动安全性，具有十分重要工程意义。欧美等发达国家率先开展了轨道车辆的碰撞安全性研究，制定了相关碰撞法规[1-3]，对列车强度设计和碰撞计算场景等提出了要求，并在铁道车辆的设计中了得到应用，提升了车辆的耐撞性能。我国在列车被动安全防护技术方面的研究起步较晚，但发展迅速，自7.23甬温线事故以来，轨道车辆的被动安全性更是被提到一个非常重要的地位，开展了大量相关研究[4-7]，但都以单节车耐撞性能的研究为主。与汽车、船舶等交通工具单体撞击不同，列车由多节车辆编组而成，列车各端部吸能结构的匹配情况对列车的耐撞性能有着十分重要的影响。因此对列车被动安全性的研究，不仅要考虑单节车耐撞性能，还要考虑各端部吸能结构的匹配关系。当列车发生碰撞事故时，撞击能量主要集中在头部，很大一部分能量是由头车的主吸能结构来吸收。主吸能结构的长度越长，吸收的能量就越多、撞击缓冲的时间就越长，这有利于提高列车的耐撞性能。但是主吸能结构过长会对机车的外形和结构设计造成巨大的挑战，所以在满足耐撞性需求的前提下应尽量减小头部主吸能结构的长度。本文以国内某新造200km/h客运电力机车为例，开展25km/h碰撞速度下的机车耐撞性设计工作，以头部主吸能结构的变形量作为目标参数，吸能结构的特性曲线为设计变量，通过调整车端吸能结构特性曲线，实现碰撞能量在列车各碰撞界面的合理分配，在满足耐撞性要求的前提下尽量减小头部主吸能结构的变形长度。对于车辆碰撞过程中的优化问题而言，目标参数与设计变量一般具有很强的非线性关系，很难给出目标参数随设计变量变化的显式方程，且工况的计算时间一般较长，常用的方法是借助于代理模型对试验设计生成的样本点进行拟合，得到目标函数随设计变量变化的响应曲面，再结合优化算法进行寻优求解[8-10]。优化算法有很多种，主要有人工神经网络、模拟退火法、自适应响应面法、序列二次规划和遗传算法等[11-13]，分别适用于不同的应用场合。遗传算法(GA)具有较好的全局搜索能力，简单通用，鲁棒性强，适用于解决复杂的非线性问题。本研究基于列车多刚体耦合碰撞模型，采用遗传算法直接对优化问题进行寻优，实现电力机车的前期耐撞性优化设计。

1列车纵向动力学模型

集中质量动力学模型具有模型简单、计算速度快等优点，广泛用于车辆碰撞领域，尤其是在需要大量反复计算的车辆耐撞性前期设计过程[14-15]。本文使用列车纵向动力学模型进行车辆耐撞性的前期设计。根据列车纵向动力学理论，将组成列车的各节车辆简化为单一质点，将连接相邻车辆的车钩缓冲装置考虑为非线性弹簧，非线性弹簧同时考虑了缓冲器的加载、卸载特性及吸能结构的特性曲线。该模型仅考虑了车体沿纵向的运动和变形，每个车体质点所受到的力包括与轨面之间的摩擦力、相邻车体之间的非线性弹簧力，利用牛顿第二运动定律，每个车体质点的运动方程如下：

(1)

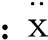
根据厂家要求，本文研究的碰撞速度为25km/h，详细碰撞场景为：2列相同类型的车组前端的碰撞，一列车组以时速不低于25km/h的速度撞击静止在同一平直轨道上未制动的另一列相同类型的车组。每列车组由被试机车和参考车辆组成，被试机车为重联两辆相同机车组成，参考车辆是一辆80t的货车；货车假定为刚性，其连接面的特性按实际连接车钩缓冲装置性能取值，机车碰撞场景如图1所示。

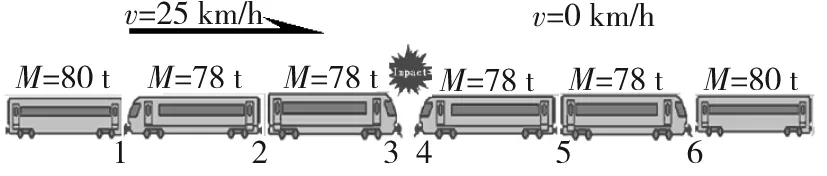
图1　撞击场景Fig.1 Collision scenario

2遗传算法的基本步骤

遗传算法[13-14]是以进化理论为依托的一类机器学习技术。与传统的优化方法不同，遗传算法是一种群体进化技术，基本步骤如图2。

1)编码。编码是遗传算法首先要解决的问题，也是设计遗传算法的一个关键步骤。在遗传算法执行过程中，对不同的具体问题进行编码，编码的好坏直接影响选择、交叉、变异等遗传运算。常用的编码方式有二进制编码，实数制编码等。

2)初始化种群。种群规模对计算效率及优化结果有着十分重要的影响。一般而言，种群规模越大，个体的多样性越高，算法陷入局部解的危险就越小，但是，种群规模太大会导致计算效率下降。另一方面，群体规模太小，会使遗传算法的搜索空间中分布范围有限，容易引起未成熟收敛现象。本文中的种群数目由以下表达式确定。

(2)

式中：GAPOPS为种群数；N为设计变量数目。

3)适应度计算。适应度是评价某个解优劣性的指标。一般而言，适应度函数是由目标函数变换而来的，如式(3)和(4)。按照达尔文适者生存的进化理论，具有高适应度的个体更有可能被选择来繁殖下一代。

若目标函数为最小化问题，则

(3)

其中：f(x) 为目标函数；x为设计变量；Cmax为目标函数的最大值估计；fit(f(x)) 为适应度值。

若目标函数为最大化问题，则

(4)

其中：f(x) 为目标函数；x为设计变量；Cmin为目标函数的最小值估计；fit(f(x)) 为适应度值。

为避免在遗传进化初期产生一些竞争力极强的超常个体，影响算法的全局优化性能。因此，在进化初期必须避免某一个个体适应度过大，通过对适应度进行尺度变换 (fitnessscaling)，改变原适应度值的比例关系。常用的尺度变换方法有线性变换法、幂函数变换法和指数变换法。

4)高适应度个体直接保存。种群中的一小部分高适应度个体直接保存至下一代，这是遗传算法保证解的质量不会降低的重要手段。其比例越高，生成新个体的比例越小，收敛速度增加，缺点是容易造成不成熟收敛。推荐使用比例为1%～20%。

5)选择算子。在当前种群中选择适应度较高的个体遗传到下一代去，选择算子体现适者生存的原理，适应度越高被选中的概率越大。Hyperstudy提供的选择范围为2～5(一般选择2)，其数值越大，意味着适应度值较低的个体被选中的概率越小，具有较高适应度值的个体拥有更大几率去繁殖下一代，但缺点是种群个体的多样性降低，易导致过早收敛。

6)交叉、变异。交叉和变异是生成新个体的重要方法。变异率越大，产生的随机效应越大，遗传算法的全局搜索效果越好，但收敛速度会降低，推荐取值范围为0.001～0.6。

7)计算终止条件。①计算收敛，迭代步数大于给定的最小迭代步数，且此时的优化解是可行的(满足约束条件)，目标函数的与上一迭代步的差值很小(不超过0.001)；②当目标函数收敛特性并不明显时，通过指定最大迭代步数终止优化过程。

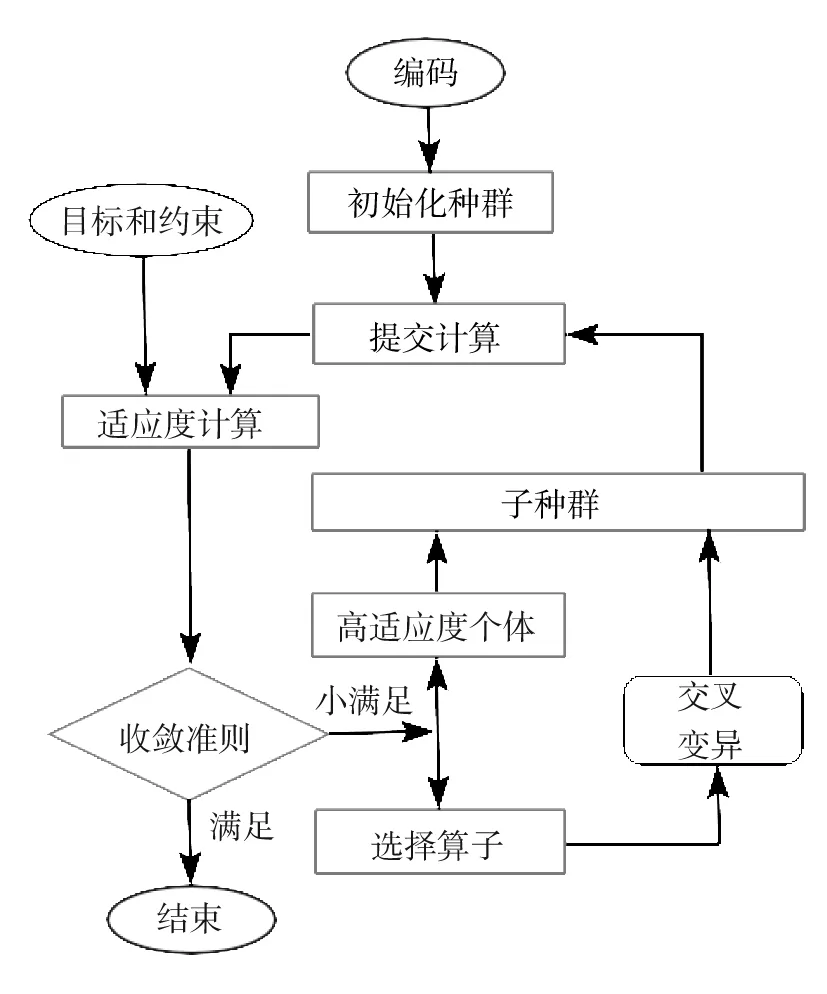
图2　遗传算法Fig.2 Genetic algorithm

3机车端部吸能结构

与动车组、地铁车辆不同，电力机车碰撞质量一般比较大。根据文献[16]，列车碰撞耗能主要集中在头部及次节车碰撞界面，并给出了头部、次节车碰撞界面的碰撞吸能量推荐公式，均与第1节运动车辆的动能成正比。这就意味着在相同的碰撞速度下，机车端部需要耗散的能量更大，对机车耐撞性结构设计提出了更高的要求。

本文研究的客运电力机车为重联2辆相同机车组成。机车头部采用三级吸能结构。车钩缓冲器为HN-1型弹性胶泥缓冲器，缓冲器容量≥80kJ，行程≤73mm，车钩缓冲器特性曲线简化为行程为73mm，最大阻抗力同下级吸能结构一致的斜线段，如图3(a)的OA段；可变形吸能元件安装于钩缓装置后，受空间限制，最大设计可变形长度为100mm，为保证车钩缓冲器在低速冲击作用下，变形吸能元件不会被触发，其设计压溃平台力的下限值取1 600kN，为避免吸能元件压溃吸能时造成车体提前塑变，平台力上限值不超过2 000kN，AB段；车体前端设计为承载式吸能结构，承载式吸能结构不仅要承受碰撞冲击时的动载荷，还要传递静态载荷，碰撞变形能量吸收区的设计必须同时兼顾静强度及碰撞安全性2个方面的要求，刚度取值范围为2 500 ～3 500kN，要求承载式主吸能结构的变形长度尽可能的小，CD段；EF段为车体载人区。

(a)机车头部吸能特性曲线;(b)重联端吸能特性曲线图3　机车端部吸能结构特性曲线Fig.3 Characteristic curves of locomotive end energy-absorbing structure

机车重联端使用二级吸能结构，连接装置为半永久性车钩，车钩一端为橡胶缓冲器，与头部相同，如图3(b)的OA段；另一端安装有压缩行程为200mm的压溃管，压溃管塑变平台力取值范围与头部变形吸能元件一致，AB段；CD段为车体载人区。表1为机车端部吸能结构的设计参数。

表1机车端部吸能结构参数

Table1Parametersoflocomotiveendenergy-absorbingstructure

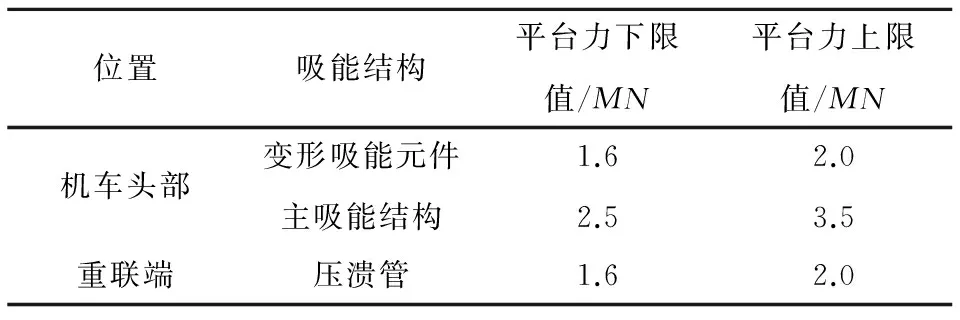
位置吸能结构平台力下限值/MN平台力上限值/MN机车头部变形吸能元件主吸能结构1.62.52.03.5重联端压溃管1.62.0

4机车耐撞性优化设计

车辆碰撞过程中的能量耗散，并不是简单的将各部分吸能结构的设计吸能量相叠加，车辆端部吸能结构的压溃平台力的匹配情况对列车撞击时各个撞击界面的形变和吸能量有十分重要的影响。

本文开展动力学仿真计算，基于多体动力学软件MADYMO建立机车纵向多刚体耦合碰撞模型，研究头部变形吸能元件塑变平台力x1，头部主吸能结构塑变平台力x2和重联端压溃管撞击塑变平台力x3，对机车耐撞性能的影响，设计一组吸能结构特性参数，实现机车在碰撞过程中的有序、可控吸能，优化头部主吸能结构的变形长度。

电力机车的头部主吸能结构的优化问题可描述为：以D1(头部主吸能结构的变形量)为目标参数，x1，x2和x3为设计变量，在重联端压溃管压缩量d2不超过行程的约束条件下，变化x1，x2和x3生成一系列样本点，利用动力学仿真分析求出样本点处的D1，使用二阶响应面法拟合试验样本点，分析各设计变量对目标参数的影响规律，使用遗传算法对优化问题直接求解。表2为优化问题的数学模型。

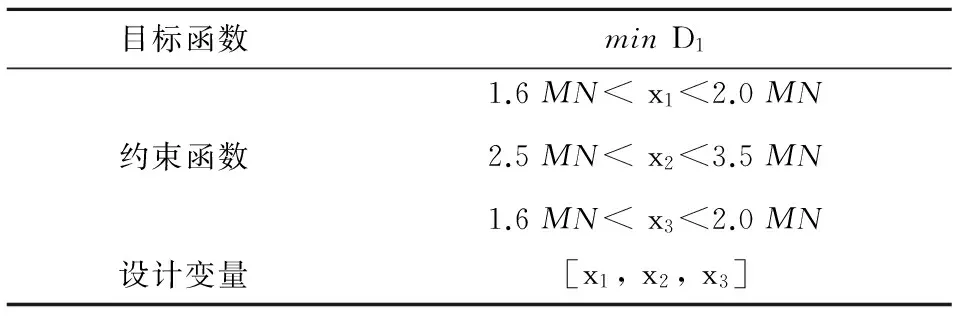
表2　机车耐撞性优化数学模型

4.1试验样本及计算

采用全因子设计方法进行取样。设计变量x1和x3选取5个取值水平，由于设计变量x2的取值范围较大，因此适当加大取值密度，取值水平数为11。本次试验设计的计算次数为5·5·11=275次。表3为仿真得到的部分结果。

采用二阶响应面拟合试验样本点，可以得到各设计变量间的交互作用对目标参数D1和约束条件d2的影响，如图4～5所示。由图4～5可以看出，D1及d2随设计变量变化的一般规律，在设计区间范围内，设计变量x1对D1和d2的影响相对较小，x1增加，D1缓慢减小，d2缓慢增加。D1和d2主要受x2和x3的影响。D1随x2的增加而呈减小的趋势，随x3的增加而呈增加的趋势，但随着x2的增加，x3对D1的影响会越来越小；d2随x2的增加而增加，随x3的增加而减小。

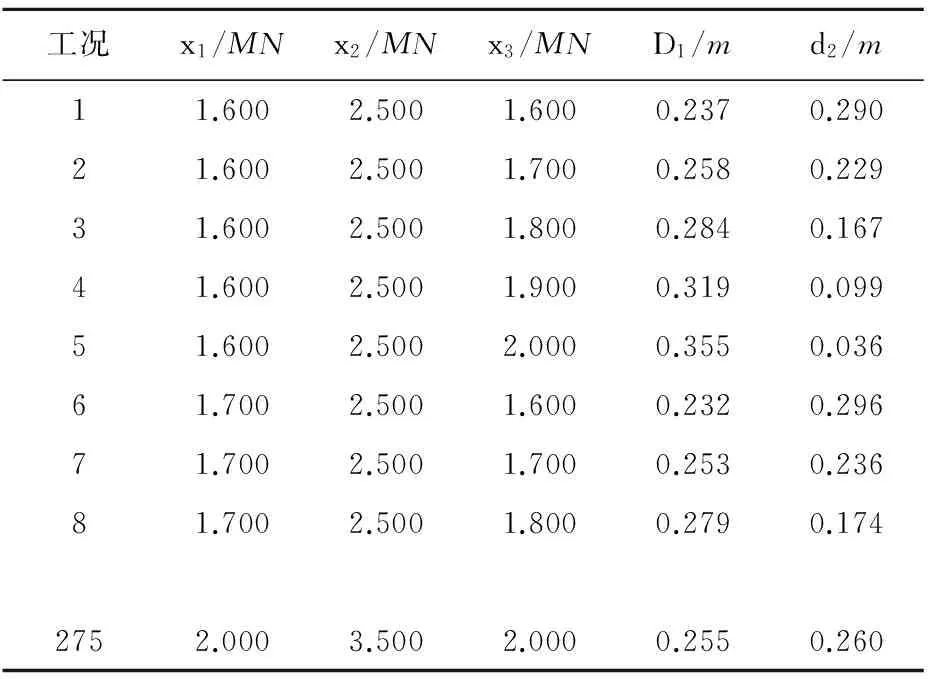
表3　部分计算结果

(a)x1和x2交互作用响应面：D1；(b)x2和x3交互作用响应面：D1；(c)x1和x3交互作用响应面: D1图4　二阶交互作用响应面: D1Fig.4 Quartic interpolated response surface: D1

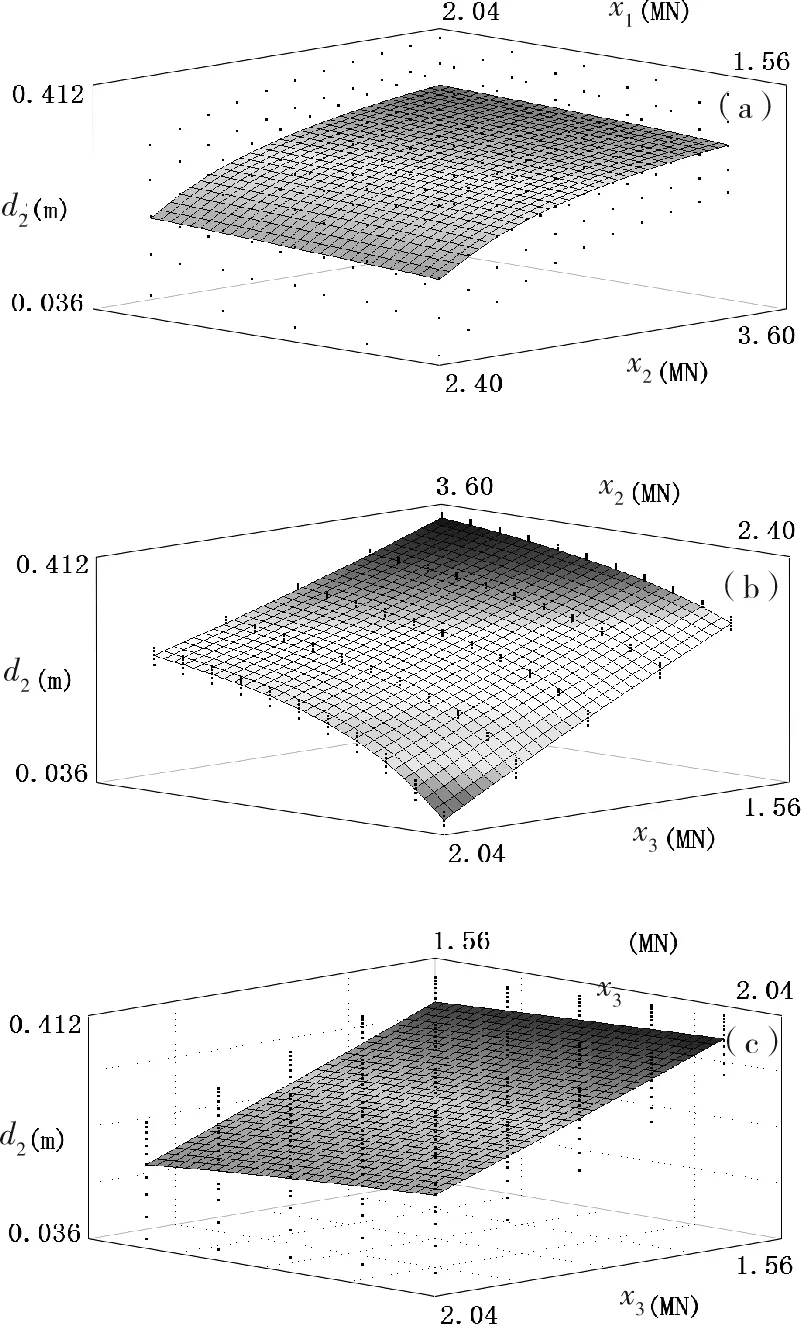
(a)x1和x2交互作用响应面: d2；(b)x2和x3交互作用响应面：d2；(c)x1和 x3交互作用响应面: d2图5　二阶交互作用响应面: d2Fig.5 Quartic interpolated response surface: d2

4.2优化求解

本文采用的计算模型为列车纵向多刚体碰撞模型，计算速度快，每个工况的计算时间约为10s，因此优化过程中直接调用动力学求解器求解，而不借助于代理模型，具有更高的计算精度，优化流程如图6。

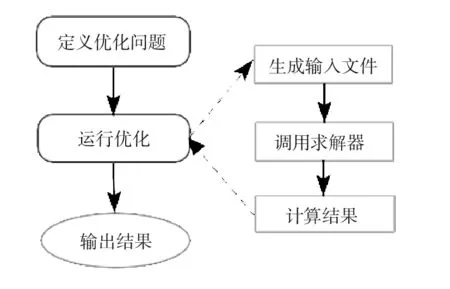
图6　直接调用求解器优化方法Fig.6 Optimization using the analysis solver directly

客运电力机车的耐撞性优化为带约束的目标参数最小化问题，采用遗传算法直接对优化模型进行整体寻优。在设计区间范围内任意选取1组参数(x1=2.0MN，x2=2.8MN，x3=2.0MN)作为计算初值，迭代30步(最大迭代步数为100，最小迭代步数为25)后计算收敛，此时x1=1.615MN，x2=3.130MN，x3=1.999MN，目标参数D1=0.178m，约束条件d2=0.199m。迭代历程如图7。

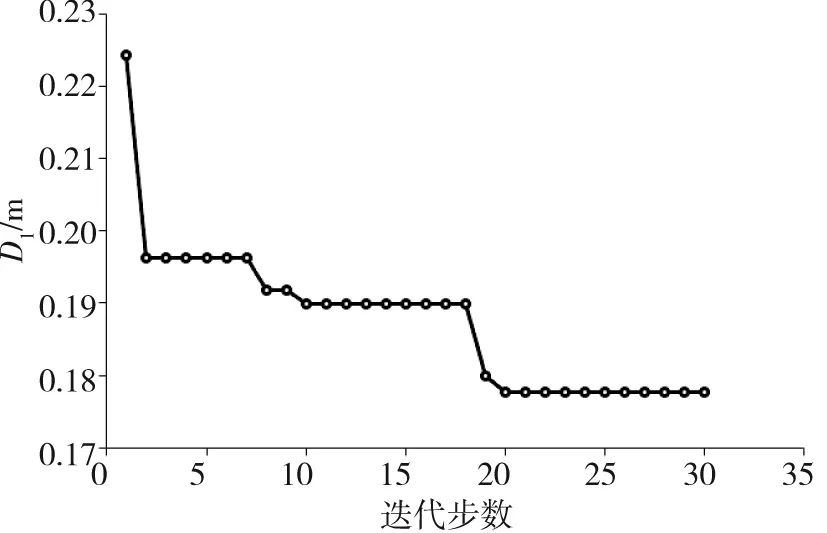
图7　　D1的优化历程Fig.7 Values of D1 in the progress of optimization

其中设计变量x1的优化值接近于设计区间的下限，这是因为在设计区间范围内，变量x1对于约束d2的作用显著于其对D1的作用，其在优化过程中的主要作用是减缓d2的上升趋势；虽然增加x2，减小x3均可以减小D1，但随着x2的增加，x3对D1的影响会越来越小，相对于对D1的影响，x3对约束d2有着更为显著的作用，x3的增加可以很大程度上减缓d2随x2增加而增加的趋势，因此设计变量x3的优化值接近于区间的上限值；变量x2的取值水平是决定D1大小的最重要因素，x2的增加可大幅度减小D1的值，但同时也会导致约束d2增加，目前优化的x2取值接近于约束允许的最大值，继续增加会使得约束超过允许范围。

当x1=1.615MN，x2=3.130MN，x3=1.999MN时的详细计算结果如图8～9。

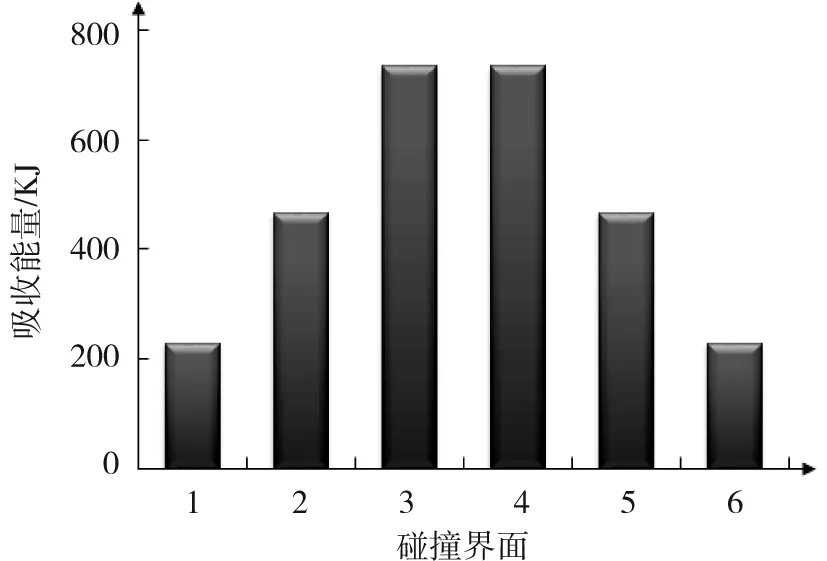
图8　各碰撞界面的能量耗散Fig.8 Energy absorbed distribution on each collision interface

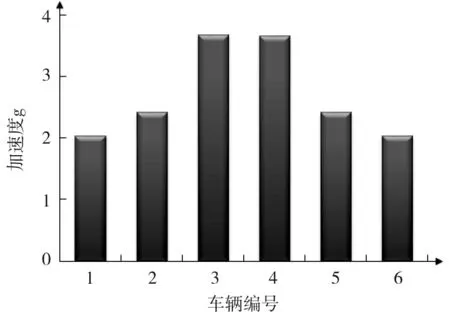
图9　碰撞过程中车辆的最大加速度Fig.9 Maximum acceleration of each vehicle during collision

碰撞过程中的能量耗散主要集中在2-4碰撞界面，车辆的最大加速度不超过5G，机车满足耐撞性要求。

5结论

1)使用二阶响应面对试验设计的样本点进行拟合，得到设计变量关于目标参数和约束条件的变化规律。在设计区间范围内，头部主吸能结构塑变平台力x2是决定D1大小的最重要因素，变形吸能元件塑变平台力x1和重联端压溃管塑变平台力x3主要起减缓约束d2增加的作用。

2)基于遗传算法对建立的优化模型进行整体寻优，优化过程中直接调用动力学求解器进行计算，而不借助于代理模型，具有更高的精度。

3)当x1=1.615MN，x2=3.130MN，x3=1.999MN时，头部主吸能结构的变形长度D1可缩短至0.178m，机车满足25km/h碰撞速度下耐撞性要求，研究结果可用于指导机车的耐撞性设计。

参考文献:

[1]EN12663,Railwayapplications-structuralrequirementsofrailwayvehiclebodies[S].2000.

[2]EN15227,Crashworthinessrequirementsforrailwayvehiclebodies[S]. 2008.[3]GM/RT2100,Structuralrequirementsforrailwayvehicles[S].2000.

[4] 田红旗, 许平. 吸能列车与障碍物撞击过程的研究和分析[J]. 长沙铁道学院学报, 2002, 20(3): 55-60.

TIANHongqi,XUPing.Analysisofcollisionbetweenenergy-absorbingtrainandbarrier[J].JournalofChangshaRailwayUniversity, 2002, 20(3): 55-60.

[5] 张在中, 姚曙光. 城市轨道车辆吸能结构设计[J]. 铁道科学与工程学报, 2013, 10(3): 94-98.

ZHANGZaizhong,YAOShuguang.Designofenergyabsorptionstructureforurbantrackvehicle[J].JournalofRailwayScienceandEngineering, 2013, 10(3): 94-98.

[6] 谢素超, 田红旗, 周辉. 耐冲击地铁车辆设计及整车碰撞研究[J]. 铁道科学与工程学报, 2008, 5(5): 65-70.

XIESuchao,TIANHongqi,ZHOUHui.Thedesignofcrashworthysubwayvehicleandcrashresearchofwholecar-body[J].JournalofRailwayScienceandEngineering, 2008, 5(5): 65-70.

[7] 王文斌, 康康, 赵洪伦. 列车耐碰撞系统有限元和多体动力学联合仿真[J]. 同济大学学报(自然科学版), 2011, 39(10): 1152-1156.

WANGWenbin,KANGKang,ZHAOHonglun.Jointsimulationofcrashworthytrainsetbasedonfiniteelementandmulti-bodydynamic[J].JournalofTongjiUniversity(NaturalScience), 2011, 39(10): 1552-1556.

[8] 舒冬, 姚松. 基于微分进化算法的列车吸能方管结构耐撞性多目标优化设计[J]. 铁道科学与工程学报, 2011, 8(2): 92-96.

SHUDong,YAOSong.Multi-objectiveoptimizationdesignoftraincrashworthytubeandanalysisofenergyabsorptionbasedondifferentialevolutionalgorithms[J].JournalofRailwayScienceandEngineering, 2011, 8(2): 92-96.

[9]ZareiHR,KrögerM.Optimizationofthefoam-filledaluminumtubesforcrushboxapplication[J].Thin-WalledStructures, 2008, 46(2): 214-221.

[10] 谢素超, 周辉. 基于Kriging法的铁道车辆客室结构优化[J]. 中南大学学报(自然科学版), 2012, 43(5): 1990-1998.

XIESuchao,ZHOUHui.OptimizationonpassengercompartmentstructureofrailwayvehiclebasedonKrigingmethod[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2012, 43(5): 1990-1998.

[11]YangSY,WuL,YangL,etal.Robustorientedparticleswarmoptimizationalgorithmappliedtoinverseproblems.International[J].JournalofAppliedElectromagneticsandMechanics, 2012, 33(3-4): 1057-1062

[12]SońskiM.Acomparisonofmodelselectionmethodsforcompressivestrengthpredictionofhigh-performanceconcreteusingneuralnetworks[J].Computers&Structures, 2010, 88(21): 1248-1253.

[13] 梁昔明, 朱灿, 颜东煌. 基于物种选择的遗传算法求解约束非线性规划问题[J]. 中南大学学报(自然科学版), 2009, 40(1): 185-189.

LIANGXiming,ZHUCan,YANDonghuang.Novelgeneticalgorithmbasedonspeciesselectionforsolvingconstrainednonlinearprogrammingproblems[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2009, 40(1): 185-189.

[14] 葛继科, 邱玉辉, 吴春明,等. 遗传算法研究综述[J]. 计算机应用研究, 2008, 25(10): 2911-2916.

GEJi-ke,QIUYuhui,WUChunming,etal.Summaryofgeneticalgorithmsresearch[J].ApplicationResearchofComputers, 2008, 25(10): 2911-2916.

[15]DiasJP,PereiraMS.Optimizationmethodsforcrashworthinessdesignusingmultibodymodels[J].ComputersandStructures, 2004, 82(17): 1371-1380.

[16]LuG.Energyabsorptionrequirementforcrashworthyvehicles[J].ProceedingsoftheInstitutionofMechanicalEngineers.PartF:JournalofRailandRapidTransit, 2002, 216(1): 31-39.

* 收稿日期：2015-10-21

基金项目：国家自然科学基金重点资助项目(U1334208)；国家科技支撑计划项目(2015BAG12B01)

通讯作者：姚曙光( 1970-)，女，湖南邵阳人，博士，从事车辆结构设计研究；E-mail：ysgxzx@csu.edu.cn

中图分类号：U264.0

文献标志码：A

文章编号：1672-7029(2016)06-1186-07

Optimization on electric passenger locomotive crashworthiness design based on genetic algorithm

ZHANG Kai, XU Ping, YAO Shuguang

(KeyLaboratoryofTrafficSafetyonTrackofMinistryofEducation,SchoolofTrafficandTransportationEngineering,CentralSouthUniversity,Changsha410075,China)

Abstract：In order to ensure a new electric passenger locomotive absorbs energy in a regular and controllable way at the collision speed of 25 km/h, a set of vehicle end energy-absorbing structure characteristic curves were designed and the deformation length of the head main energy-absorbing structure was optimized according to the actual demands of the manufacturers. The optimization model of objective parameter (compression value D1 of main energy-absorbing structure in locomotive head) and design variables (plastic deformation platform force of collapse tube in locomotive head x1, plastic deformation platform force of main energy-absorbing structure in locomotive head x2, plastic deformation platform force of collapse tubes in reconnection end x3) were built under the constraint condition (compression value of the collapse tube in reconnection end d2). The optimal absorbing structure characteristic curves were obtained by the optimization model using genetic algorithm (GA) directly. The study indicated that when D1 reached the minimum value 0.178 m, x1=1.615 MN, x2=3.130 MN and x3=1.999 MN. Also, the locomotive meets the crashworthiness requirements. The results are helpful to guide the crashworthiness design of locomotive.

Key words：electric passenger locomotive; train longitudinal dynamics; crashworthiness design; optimization; genetic algorithm