基于选取不同剪力滞广义位移的薄壁箱梁剪力滞效应研究

张玉元，张慧,2，李巍，杨娟

(1.兰州交通大学 土木工程学院，甘肃 兰州 730070；2.兰州交通大学 甘肃省道路桥梁与地下工程重点试验室，甘肃 兰州 730070；3.西南交通大学 土木工程学院，四川 成都 614202；4.甘肃省陇南公路管理局，甘肃 陇南 746000)



基于选取不同剪力滞广义位移的薄壁箱梁剪力滞效应研究

张玉元1，张慧1,2，李巍3，杨娟4

(1.兰州交通大学 土木工程学院，甘肃 兰州 730070；2.兰州交通大学 甘肃省道路桥梁与地下工程重点试验室，甘肃 兰州 730070；3.西南交通大学 土木工程学院，四川 成都 614202；4.甘肃省陇南公路管理局，甘肃 陇南 746000)

摘要:基于箱梁顶板、悬臂板、底板具有不同的翘曲程度，考虑各个翼板应选取不同的最大剪切转角差为剪力滞广义位移。以顶板、悬臂板和底板采用不同的最大剪切转角差和相同的最大剪切转角差2种情况，应用能量变分原理分别推导出单室箱梁受竖向对称荷载下的剪力滞效应微分方程，结合边界条件导出相应的闭合解。针对典型的简支箱梁为算例，利用数值方法和本文解析解方法，研究了满跨均布力和跨中集中力作用下跨中截面的测点应力解，对斜腹板箱梁算例而言，采用不同最大剪切转角差获得的纵向应力解和高阶样条法计算的纵向应力解的误差比较小，基本在4%以内，验证了解析解具有良好的精度；对直腹板箱梁而言，取不同最大剪切转角差的应力解析解更贴近数值解，误差比基本在6%以内，研究表明：各个翼板取不同最大剪切转角差的假设是正确合理的，能够精确的反映剪力滞规律。

关键词：单室箱梁；剪力滞效应；能量变分法；最大剪切转角差；有限元

薄壁箱梁因其有利的受力特性而被广泛应用于现代桥梁工程中。薄壁箱梁发生竖向挠曲变形时，由腹板传递给翼缘板的剪力流使翼缘板在远离腹板处的纵向位移滞后于靠近腹板处的纵向位移，从而使箱梁翼缘板不满足平截面假设，这就是剪力滞效应[1-2]。在薄壁箱梁设计计算中，如果不考虑剪力滞效应的影响，计算得到的挠度值比实际小，不能客观反映箱梁的变形和承载内力，从而对结构造成安全隐患，甚至造成重大事故。当今大悬臂薄壁混凝土箱梁广泛应用于现代桥梁建设中，因此考虑剪力滞对箱梁的影响是有必要的。能量变分原理是研究剪力滞效应常采用的方法之一，运用此方法求解剪力滞效应时，有两个问题需要探讨，第一，剪力滞翘曲位移函数的选定，目前常采用的有抛物线和余弦函数，何余良等[3-5]均采用抛物线为剪力滞翘曲位移函数，国内学者采用抛物线的很多，但是采用余弦函数作为剪力滞翘曲位移函数的学者很少，倪元增[6]在国内提出余弦函数作为剪力滞翘曲位移函数，雒敏等[7]在倪元增等的理论基础上将单箱单室箱梁理论推广到单箱双室，本文采用余弦函数作为剪力滞翘曲位移函数，有如下理由：余弦函数展开成幂级数，从展开式中可以看出是由若干个高次式构成，而这若干个高次式正是抛物线函数里面的二次、三次抛物线等，即抛物线是余弦函数展开式中的某一项，从精度上讲，余弦函数更合适；第二，剪力滞广义位移的确定，常采用的有最大剪切转角差和附加挠度2种、张元海等[1,5]采用附加挠度作为剪力滞广义位移，蔺鹏臻等[9-10]采用箱梁顶板、悬臂板、底板采用相同的最大剪切转角差作为剪力滞广义位移，甘亚楠等[11-12]、考虑到顶板、悬臂板、底板具有不同的翘曲程度，张元海[13]中选取悬臂板和顶板等宽的直腹板单室箱梁为例，从算例实测值和有限元数值解来看，悬臂板端部处的应力值小于顶板中心处的应力值，由此可见应该考虑各个翼板采用不同的最大剪切转角差作为剪力滞广义位移；选择附加挠度为剪力滞广义位移，虽然具有明确的力学意义，便于工程人员理解和使用，但是选择不同的最大剪切转角差作为顶板、悬臂板、底板的剪力滞广义位移，从计算精度上讲更合理。本文选取余弦函数为剪力滞翘曲位移函数，考虑到箱梁各个翼板具有不同的翘曲程度，故讨论各个翼板取不同的最大剪切转角差和相同的最大剪切转角差为剪力滞广义位移2种情况，应用能量变分原理分别推导出箱梁截面控制微分方程，并给出相应边界条件下的闭合解，针对一个典型的简支箱梁为例，验证本文分析方法的精度，此外，本方法计算简单，可以依靠数学软件实现，便于工程应用，可以将此方法进一步拓展到单箱多室。

1截面控制微分方程及边界条件

1.1各个翼板分别取不同最大剪切转角差时的截面控制微分方程及边界条件

如图1所示，XOY为整体坐标系，xoy为局部坐标系，箱梁在竖向任意荷载q(z)作用下的挠曲变形，选取最大剪切转角位移差作为剪力滞广义位移，则箱梁截面任意一点处的纵向位移u(x,y,z)为

u(x,y,z)=-y·w′(z)+ωζ(x,y)·U(z)

(1)其中：w(z)为竖向挠度；ωζ(x,y)为翘曲位移函数；U(z)为剪切变形最大差值；式中第1项为初等梁纵向位移，第2项为剪力滞引起的附加位移。

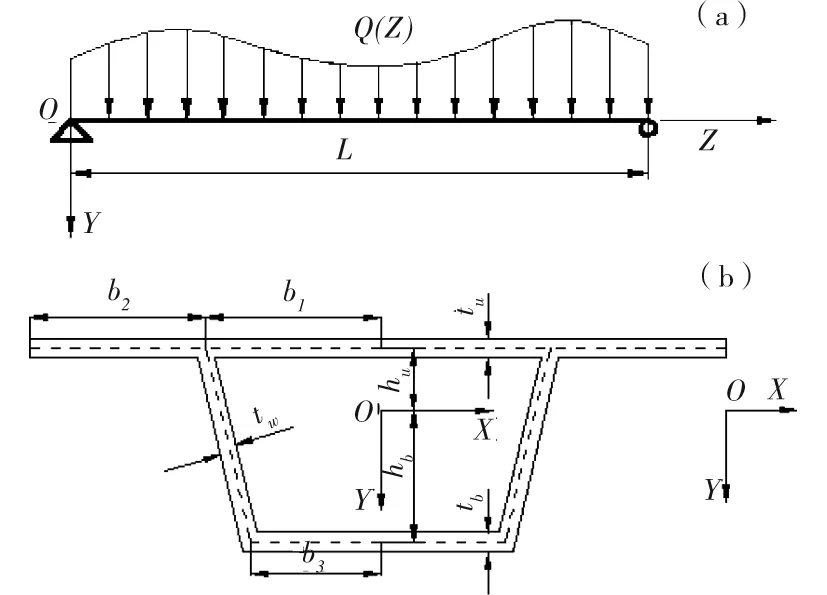
(a)坐标系及荷载；(b)横截面图1　箱型截面简图Fig.1 Box girder with cross section

式(1)中的剪力滞翘曲位移函数取：

(2)

将式(2)代入式(1)，可得顶板、悬臂板、底板的纵向位移表达式：

顶板：

u1(x,y,z)=

(3)

悬臂板：

u2(x,y,z)=hu[w′(z)+

(4)

底板：

u3(x,y,z)=-hb[w′(z)+

(5)

顶板、悬臂板和底板的应变能表达式：

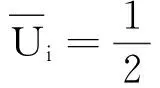
(6)

其中：

(7)

E为弹性模量；G为剪切模量。

箱梁腹板的应变能：

(8)

箱梁外力势能：

(9)

箱梁总势能：

(10)

将以上式代入式(8)可得

(11)

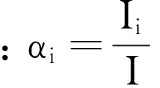
I为箱梁截面抗弯惯性矩；M为箱梁某一截面处的弯矩。

将式(11)求一阶变分，并令δπ=0

δUidz= 0

(12)

根据变分引理，由式(12)可得截面控制微分方程

(13)

(14)

(15)

将式(13)代入式(15)消去w可得

(16)

将式(16)写成矩阵的形式

(17)

其中：Q(z)为箱梁某一截面处的剪力。

求解微分方程组(17)在简支下的边界条件：

1)集中力时：

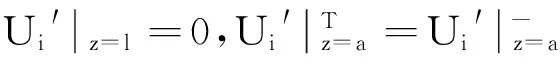
由弹性理论可得各个板的纵向应力表达式：

(18)

1.2各个翼板取相同最大剪切转角差时的截面控制微分方程及边界条件

如图1所示，可以给出顶板、悬臂板、底板纵向位移表达式：

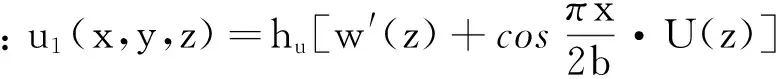
(19)

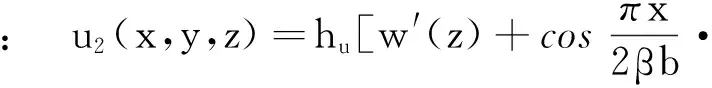
U(z)]

(20)

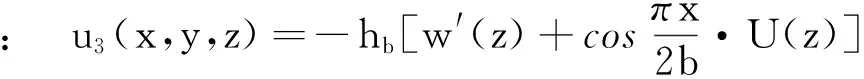
(21)

式(20)中：b1=b，b2=βb，b3=b。

将式(19)～(21)代入式(7)和式(6)，结合式(8)～(10)可得箱梁总势能：

(22)

其中：Is=Isu+Isb

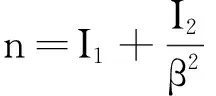
M为箱梁某一截面处的弯矩。

将式(22)求一阶变分，并令δπ=0

(23)

根据变分引理，由式(23)可得截面控制微分方程

(24)

(25)

(26)

将式(24)代入式(26)消去w可得

(27)

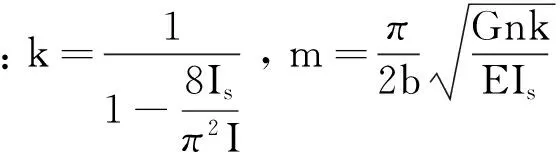
Q(z)为箱梁某一截面处的剪力。

微分方程式(27)的通解可表达为：

(28)

求解微分方程(28)在简支下的边界条件：

1)集中力时：

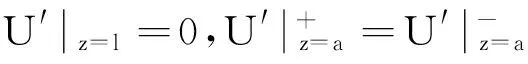
2各个翼板取相同的最大剪切转角差时简支梁剪力滞效应的应力解答

简支梁在集中力作用下如图2(a)，对应考虑剪力滞效应的应力解为:

当时

(29)

当a≤z≤l时

-shma·cthml·shmz)×

(30)

简支梁在均布力作用下如图2(b)，对应考虑剪力滞效应的应力解为：

(31)

(a)简支梁集中力图示；(b)简支梁均布力图示图2　简支梁计算简图Fig.2 Calculation diagram of simple beam

3算例

3.1斜腹板箱梁的剪力滞分析算例

以文献[9]跨度50m的简支混凝土斜腹板箱梁为例,截面尺寸、测点位置见图3，材料E=3.1×104MPa，泊松比μ=1/6。分别受2P=2×10kN和满跨均布线荷载2q=2×1kN/m。

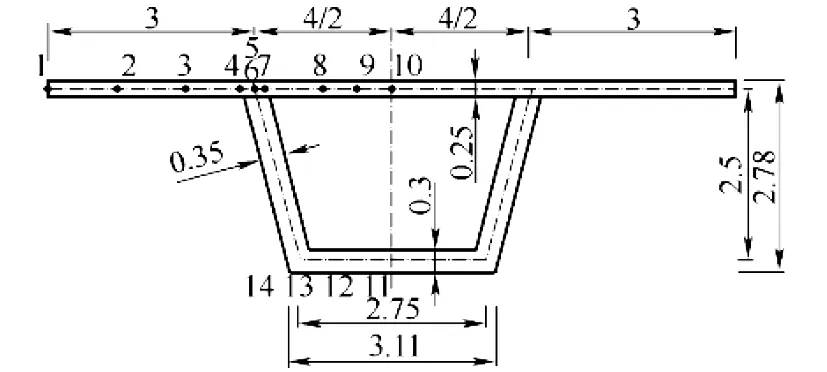
单位：m图3　截面尺寸及测点Fig.3 Cross section size

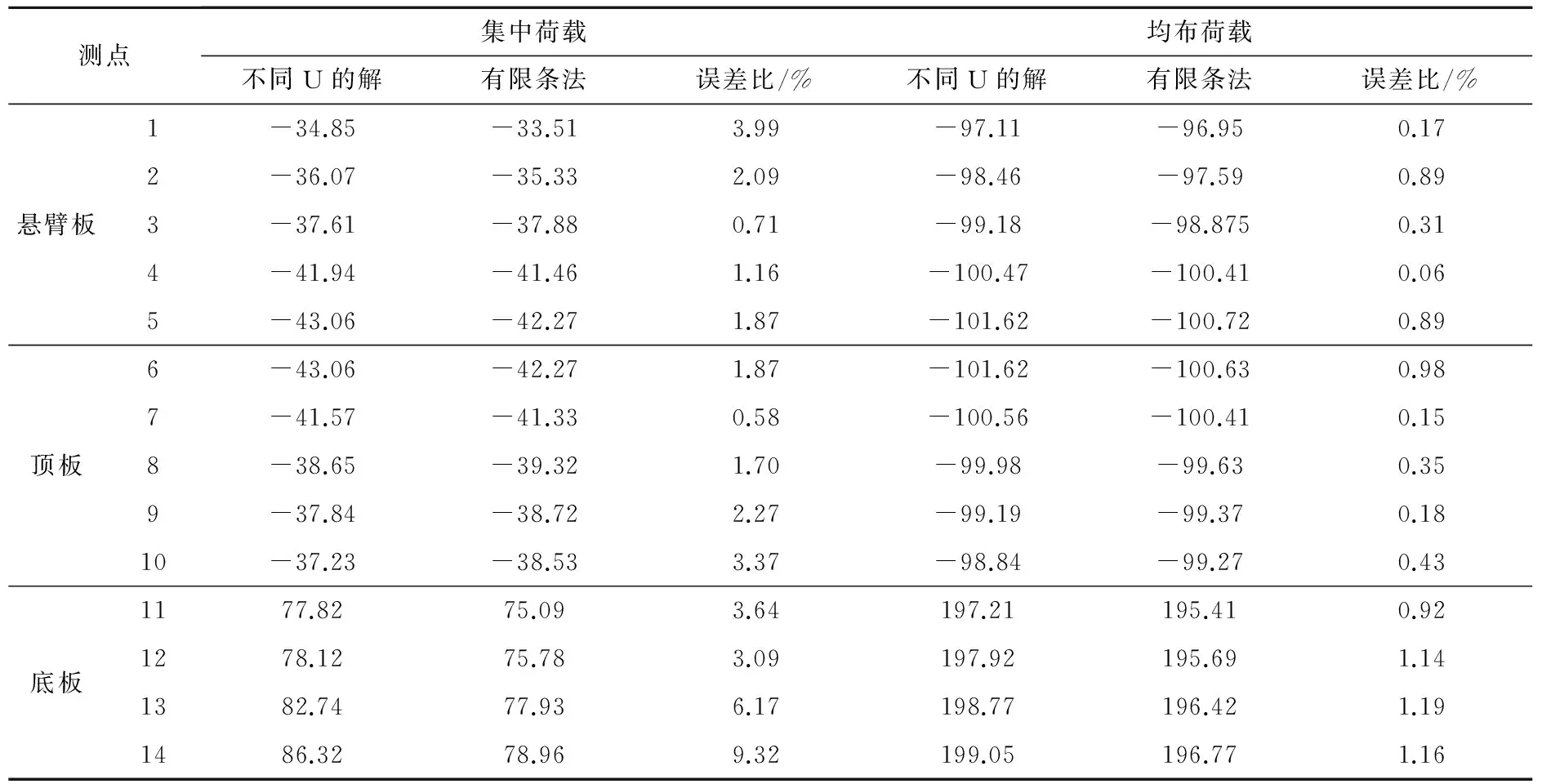
由表1可以看出：各个翼板取不同的最大剪切转角差为剪力滞广义位移，获得的测点应力值与有限样条法计算值相比，吻合良好，误差较小。集中力和均布力下，对于4号、5号、6号和7号关键点误差比在2%以内，13号和14号关键点误差比在10%以内；表中90%的测点误差比均在4%以下，10%的测点误差比在10%以内，表明本文解析解具有良好的精度。

3.2直腹板箱梁的剪力滞分析算例

在3.1中的算例，其材料特性、荷载大小和位置不变，将斜腹板改为直腹板，截面中面图尺寸、测点见图4。

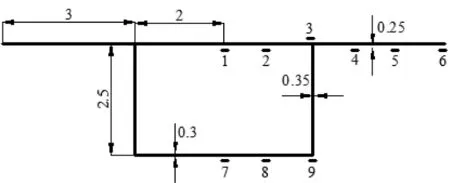
单位：m图4　截面尺寸及测点Fig.4 Cross section size

将该直腹板算例模型，沿跨度方向上每间隔5m取截面，计算简支箱梁集中力作用下的正、负剪力滞系数，绘制正、负剪力滞系数随跨度的变化图，见图5～6。

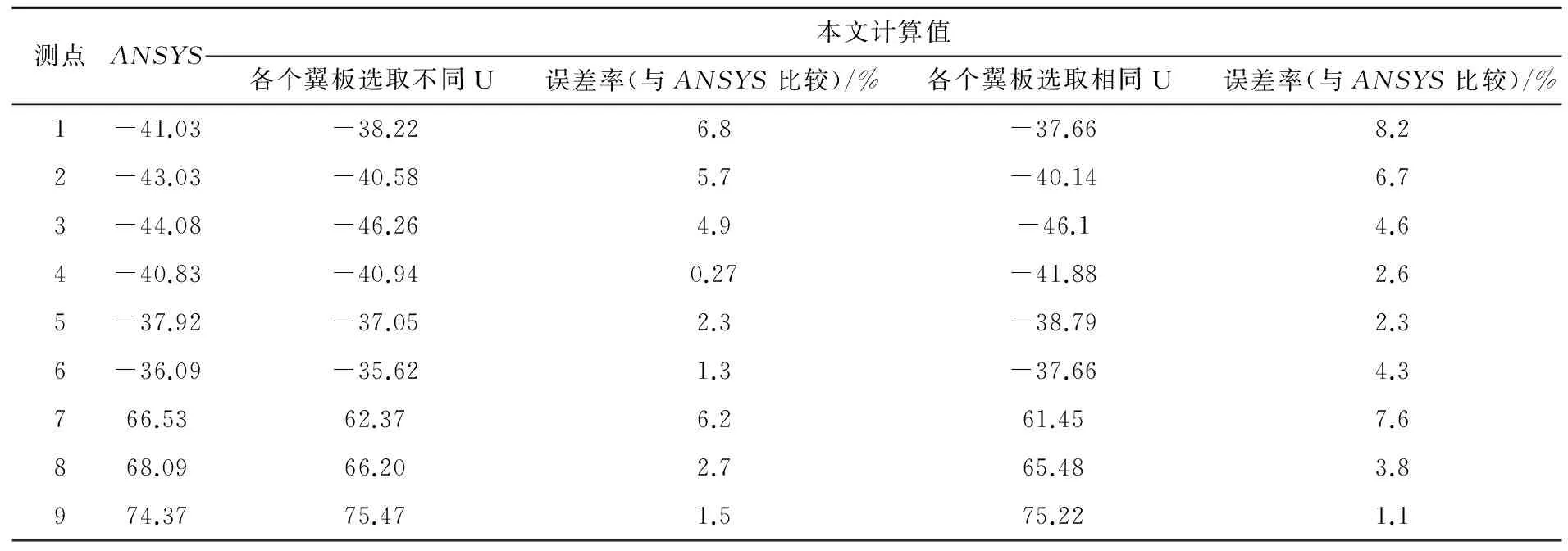
由表2～3可以看出，各个翼板分别取不同最大剪切转角差和相同最大剪切转角差为剪力滞广义位移获得的纵向应力值和Ansys板壳有限元数值解对比发现：不论是集中力还是均布力，取不同最大剪切转角差更贴近板壳有限元数值解，误差比基本在6%以内。表明各个翼板取不同剪力滞广义位移的假设是正确合理的。

由图5～6可以看出：不论是正剪力滞系数还是负剪力滞系数，基本与数值计算方法求得的剪力滞系数重合，结果表明：各个翼板取不同的最大剪切转角差为剪力滞广义位移，更能精确的反映剪力滞规律。

表1简支箱梁跨中截面应力值与有限条法计算值对比

Table1ComparisonofthecalculatedvaluesofthestressandthefinitestripmethodinthecrosssectionofthesimplesupportedboxgirderkPa

测点集中荷载均布荷载不同U的解有限条法误差比/%不同U的解有限条法误差比/%悬臂板1-34.85-33.513.99-97.11-96.950.172-36.07-35.332.09-98.46-97.590.893-37.61-37.880.71-99.18-98.8750.314-41.94-41.461.16-100.47-100.410.065-43.06-42.271.87-101.62-100.720.89顶板6-43.06-42.271.87-101.62-100.630.987-41.57-41.330.58-100.56-100.410.158-38.65-39.321.70-99.98-99.630.359-37.84-38.722.27-99.19-99.370.1810-37.23-38.533.37-98.84-99.270.43底板1177.8275.093.64197.21195.410.921278.1275.783.09197.92195.691.141382.7477.936.17198.77196.421.191486.3278.969.32199.05196.771.16

表2简支箱梁集中力作用下跨中截面应力值对比

Table2StressvaluecomparisonofcrosssectionofsimplesupportedboxgirderundertheconcentratedforcekPa

测点ANSYS本文计算值各个翼板选取不同U误差率(与ANSYS比较)/%各个翼板选取相同U误差率(与ANSYS比较)/%1-41.03-38.226.8-37.668.22-43.03-40.585.7-40.146.73-44.08-46.264.9-46.14.64-40.83-40.940.27-41.882.65-37.92-37.052.3-38.792.36-36.09-35.621.3-37.664.3766.5362.376.261.457.6868.0966.202.765.483.8974.3775.471.575.221.1

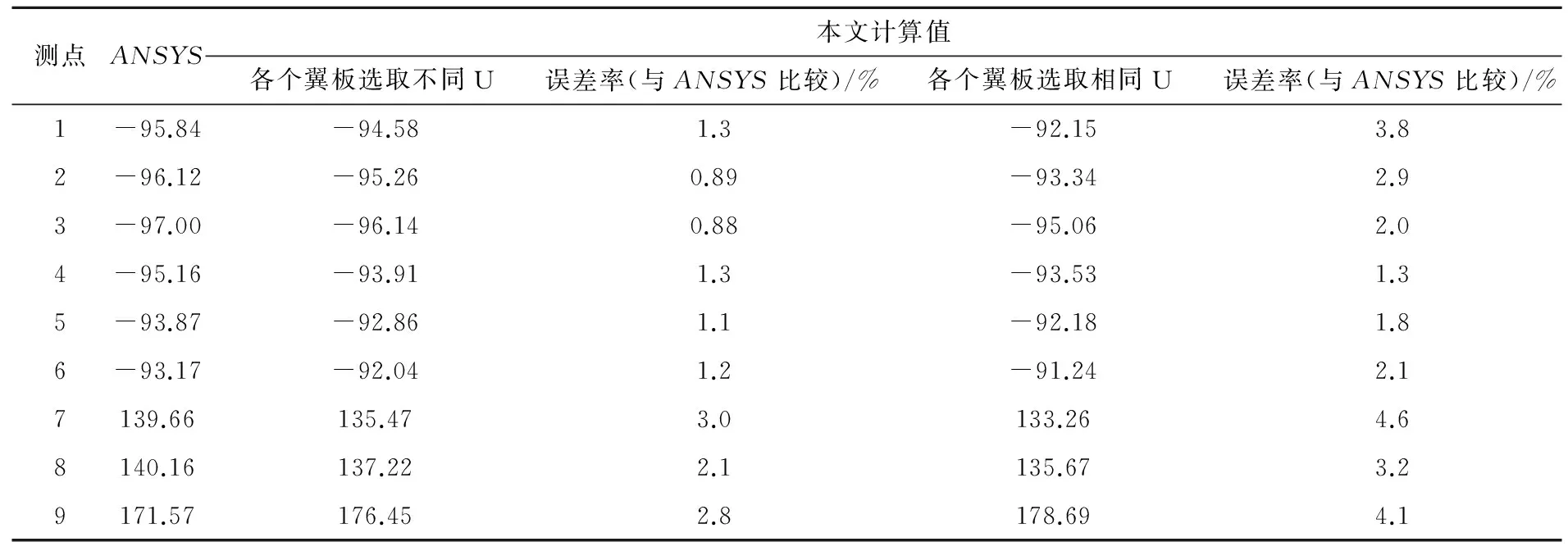
表3　简支箱梁均布力作用下跨中截面应力值对比

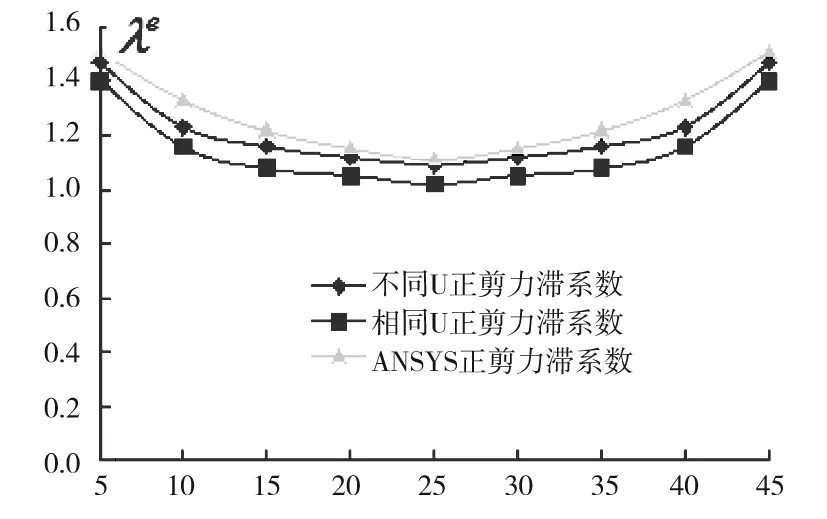
跨度/m图5　正剪力滞系数随跨度的变化图Fig.5 Variation of positive shear lag coefficient with the span

跨度/m图6　负剪力滞系数随跨度的变化图Fig.6 Variation of negative shear lag coefficient with the span

4结论

1)斜腹板下，各个翼板取不同最大剪切转角差时，获得的箱梁跨中截面各个测点纵向应力解与高阶样条数值解相比，吻合程度良好，误差比基本在4%以下，表明本文解析解具有良好的精度。

2)直腹板下，各个翼板取不同最大剪切转角差和相同最大剪切转角差时，应力理论解与有限元板壳数值解结果相比发现，取不同最大剪切转角差的结果更贴近板壳数值解，误差比基本在6%以下，表明各个翼板取不同剪力滞广义位移的假设是正确合理的。

3)从箱梁各个翼板具有不同的翘曲位移这一本质出发，考虑各个翼板选取不同的最大剪切转角差为剪力滞广义位移,通过能量变分原理推导的关于最大剪切转角差U的微分方程组，只要箱梁截面尺寸和荷载给定，就可借助数学软件求解箱梁任意截面的纵向应力，便于工程人员计算和使用。另外，借鉴文中建立两个坐标系来降低构造悬臂板剪力滞翘曲位移函数的复杂性，可将此方法进一步扩展到单箱多室的箱梁中。

参考文献：

[1]张元海，基于翘曲位移模式的薄壁箱梁剪力滞效应分析[J].土木工程学报，2015，48(6)：44-45.

ZHANGYuanhai.Analysisonshearlageffectofthin-walledboxgirdersbasedonamodifiedwarpingdisplacementmode[J].JournalofCivilEngineering,2015,48(6):44-45.

[2]项海帆，姚玲森.高等桥梁结构理论[M].北京：人民交通出版社，2000:51-60.

XIANGHaifan,YAOLinsen.Higherbridgestructuretheory[M].Beijing:ChinaCommunicationsPress,2000:51-60.

[3]何余良，项贻强，李少俊，等.基于不同抛物线函数组合箱梁剪力滞[J].浙江大学学报，2014，48(11)：1934-1940.

HEYuliang,XIANGYiqiang,LIShaojun,etal.Analysisonshearlageffectofcompositegirdersbasedondifferentparabolicwarpingdisplacementfunction[J].JournalofZhejiangUniversity, 2014,48(11):1934-1940.

[4]陈永生，田正龙，桂水荣.单箱多室波形钢腹板箱梁剪力滞研究[J].公路交通科技，2015，32(7)：69-75.

CHENYongsheng,TIANZhenglong,GUIShuirong.Researchonshearlagofsingle-boxmulti-cellgirderwithcorrugatedsteelwebs[J].HighwayTrafficScienceandTechnology, 2015,32(7):69-75.

[5]张元海，白昕，林丽霞.箱梁剪力滞效应的改进分析方法研究[J].土木工程学报，2012，45(11)：153-158.

ZHANGYuanhai,BAIXin,LINLixia.Animproveapproachforanalyzingshearlageffectofboxgirders[J].JournalofCivilEngineering,2012,45(11):153-158.

[6]倪元增.槽型宽梁的剪力滞问题[J].土木工程学报，1986，19(4)：32-41.

NIYuanzeng.Theshearlagproblemofawidebeamwithaslot[J].JournalofCivilEngineering,1986,19(4):32-41.

[7]雒敏，蔺鹏臻，孙理想.单箱双室箱梁的剪力滞效应分析[J].力学与实践，2013，35(6):70-74.

LUOMin,LINPengzhen,SUNLixiang.Analysisofshearlageffectoftwin-cellboxgirders[J].JournalofMechanicsandPractice,2013,35(6):70-74.

[8]杨绿峰，周月娥.基于挠度的剪力滞系数分析箱梁剪力滞效应[J].防灾减灾工程学报，2013，33(5):494-496.

YANGLvfeng,ZHOUYuee.Applicationofdeflection-basedshearlagcoefficienttoanalysisofshearlageffectofbox-girders[J].JournalofDisasterPreventionandMitigationofEngineering,2013,33(5):494-496.

[9]蔺鹏臻，周世军.基于剪切变形规律的箱梁剪力滞效应研究[J].铁道学报，2011，31(3):100-104.

LINPengzhen,ZHOUShijun.Analysisonshearlageffectofboxgirdersbasedonflange-slabshearlagdeformationlaw[J].JournaloftheChinarailwaySociety,2011,31(3):100-104.

[10]冀伟，吴焕庆，刘世忠.附加轴向位移对薄壁箱梁翼板应力的影响[J].公路交通科技，2013，30(9):69-73.

JIWei,WUHuanqing,LIUShizhong.Influenceofadditionalaxialdisplacementonflangestressofthin-walledboxgirder[J].HighwayTrafficScienceandTechnology, 2013,30(9):69-73.

[11]甘亚楠，石飞停.梯形箱梁剪力滞后效应的精细化分析[J].计算力学学报，2014，31(3):351-356.

GANYanan,SHIFeiting.Thedelicateanalysisofshearlageffectontrapezoidalboxgirders[J].JournalofComputationalMechanics,2014,31(3):351-356.

[12]吴幼明，罗旗帜，岳珠峰.薄壁箱梁剪力滞效应的能量变分法[J].工程力学，2003，20(4)：161-165.

WUYouming,LUOQizhi,YUEZhuFeng.Energy-variationalmethodoftheshearlageffectinthin-walledboxgirder[J].EngineeringMechanics, 2003,20(4):161-165.

[13]张元海.箱形梁桥剪滞效应和温度效应理论研究及其应用[D].成都:西南交通大学，2008:21-30.

ZHANGYuanhai,Theoreticalstudyandapplicationofshear-lagandtemperatureeffectinbox-girderbridges[D].Chengdu:SouthwestJiaotongUniversity,2008:21-30.

* 收稿日期：2015-09-05

基金项目：2015人社部留学人员科技活动项目择优资助；国家自然科学基金资助项目(51508255,50968008,51168030)；教育部“长江学者和创新团队发展计划”资助项目(IRT1139)

通讯作者：张慧(1979-)，女，甘肃兰州人，副教授，博士研究生，从事桥梁结构设计理论的研究；E-mail:252757963@qq.com

中图分类号：U441+.5

文献标志码：A

文章编号：1672-7029(2016)06-1083-01

Analysis on shear-lag effect of box girders based on different shear-lag generalized displacement

ZHANG Yuyuan1, ZHANG Hui1,2, LI Wei3，YANG Juan4

(1.SchoolofCivilEngineering,LanzhouJiaotongUniversity,Lanzhou730070,China;2.KeyLaboratoryofRoad&BridgeandUndergroundEngineeringofGansuProvince,LanzhouJiaotongUniversity,Lanzhou730070,China;3.SchodofCivilEngineering,SouthwestJiaotongUniversity,Chengdu614202,China;4.LongnanHighwayAdministrationBureauProvince,Longnan746000,China)

Abstract：It is fourd that the box girder roof, the cantilever plate and the bottom plate have different levels of warping, and each wing should select different maximum shear angle difference as the shear lag of generalized displacement. All wings utilization of different maximum shear angle difference and same maximum shear angle difference as shear-lag generalized displacement, and energy variational principle is applied to deduce respectively shear-lag differential equations of single-cell box girder under the vertical symmetrical load. Closed solutions are also derived by the use of boundary conditious. A typical example of simple box girders,using the numerical method and the analytic solution method in this paper isused to study the stress solution of measuring point in middle span under the uniform force and concentrated force.For inclined web box girder,absolute error rate of using different maximum shear angle difference to obtain the longitudinal stress solution and high step spline solution is very small,about within 4%, verify the analytical solution has good accuracy;For direct web box girder,the stress solution of the wings selection of different maximum shear angle difference is closer to analytical solution, the error ratio is lower than 6%. Research shows that: the assumption of each wing take different maximum shear angle difference as shear-lag generalized displacement is correct and reasonable, can accurately reflect the law of shear-lag.

Key words：single-cell box girder; shear-lag effect; energy variational method; maximum shear angle difference; finite element