基于机器学习的建筑能耗模型适用性研究

田 玮，魏 来，李占勇，孟庆新，宋继田，杨 松（. 天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津科技大学机械工程学院，天津 300；. 天津科技大学后勤集团，天津 300）

基于机器学习的建筑能耗模型适用性研究

田 玮1，魏 来1，李占勇1，孟庆新2，宋继田1，杨 松1
（1. 天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津科技大学机械工程学院，天津 300222；2. 天津科技大学后勤集团，天津 300222）

为进一步分析不同机器学习方法用于建筑能耗模型的适用性，重点比较了6种常用机器学习方法用于预测办公建筑能耗时的准确性，包括线性回归、高斯过程、多元自适应回归样条法、自助多元自适应回归样条法、随机森林和支持向量机.结果表明：多元自适应回归样条法、自助多元自适应回归样条法和随机森林法适用于取暖能耗的模型建立；对于制冷能耗预测，自助多元自适应回归样条法的计算精度最高.同时发现制冷能耗与取暖能耗相比，由于存在更加复杂的非线性关系，其预测难度更大.研究结果不仅可用于在建筑节能分析中确定最佳机器学习方法，而且所得机器学习方法可用于城市建筑能耗模型的建立.

建筑节能；能耗模型；机器学习；模型精度

2013年我国建筑能耗约占全国能源消费总量的19.5%，［1］.因此，为了实现经济可持续发展，推进生态文明建设，我国正在大力推进建筑节能工作［2-3］.建立可靠的能耗模型是建筑节能研究中的重要任务之一.这是因为准确的建筑能耗模型不仅可用于单体新建建筑和既有建筑的节能改造，而且对制定区域性的节能政策有直接指导作用.建筑能耗模型通常是基于热平衡原理的动态建筑能耗模拟，常用的程序包括DEST、EnergyPlus、eQUEST等.这类模型的特点是可以分析不同节能方案对于能耗的影响，确定最优节能措施；其缺点是计算耗时，建模所需时间较长.特别是在建筑能耗不确定性分析、敏感性分析、最优化设计、参数化分析、区域建筑能耗评估时，往往需要大量的模拟计算［4］，根据动态能耗模拟的建筑能耗模型，不能适用于这些场合.一种新的处理方法，是建立有特定参数的机器学习模型，在对其可靠性进行有效评估后，用于需要大量计算的建筑能耗分析中.特定参数指建筑能耗研究中最关注的分析变量，并不考虑其他无关的因素.

国内外学者已经对基于机器学习方法的建筑能耗模型进行了很多研究［4-8］：Tian等［7］利用多元自适应回归样条法得到了英国伦敦中学建筑的能耗模型；Capozzoli等［5］利用多元线性回归和分类回归树模型探讨了意大利北部80所学校的能耗特点；Le等［6］根据支持向量机算法，研究了建筑中遮阳控制的相关计算；Tian等［8］基于高斯过程和主成分回归等机器学习算法，分析了美国佐治亚理工学院校园建筑的能耗特点.目前，还缺少系统地比较这些不同机器学习算法性能的研究.导致的问题是，在建筑能耗分析中对机器学习方法的选择没有明确的标准.

因此，本研究选取典型的办公建筑，比较6种常用机器学习方法用于能耗预测时的适用性，包括线性回归、高斯过程、多元自适应回归样条法、自助多元自适应回归样条法、随机森林和支持向量机.为了提供更可靠的分析，在我国5个不同气候分区中分别选择1个城市，比较6种能耗模型在这5个城市中的预测精度.研究结果为在节能改造中选取可靠的机器学习方法提供了依据，同时可用于城市规模的建筑能耗预测研究.

1 办公建筑能耗模型

1.1 气象数据

建筑所在地区的气候状况对建筑热性能有非常显著的影响.研究中采用的全部气象数据来自于由中国气象局气象信息中心和清华大学建筑技术科学系共同编制的《中国建筑热环境分析专用气象数据集》［9］，包括气温、太阳辐照、相对湿度等.从建筑热工设计的角度，以最冷月和最热月的平均气温为主要分区指标，将全国分为严寒、寒冷、夏热冬冷、夏热冬暖和温和5个地区.在5个不同气候分区中分别选择1个城市，选定为哈尔滨、北京、上海、广州和昆明，利用其气象数据进行建模.5个城市的月平均气温变化情况见图1.

1.2 建筑动态能耗模型建立

研究选定的典型办公建筑根据《公共建筑节能设计标准》［10］确定主要参数.表1列出不同气候分区中外围护结构的热工性能参数.照明功率密度和电器设备功率峰值为10，W/m2和15，W/m2，人员密度设定为5，m2/人.内部得热（包括人员、照明和设备）的时刻表也参照《公共建筑节能设计标准》.暖通系统使用风机盘管系统提供建筑内部的通风、取暖和制冷，风机盘管系统在工作日的运行时间为8：00—18：00，取暖温度和制冷温度分别设定为20，℃和26，℃.建筑热性能评估采用的指标是单位建筑面积的年取暖和制冷能耗（单位：kW·h/m2）.

图1 5个城市的月平均气温Fig. 1 Average temperature by month in five cities

表1 5个城市的外围护结构热工性能参数Tab. 1Thermal properties of building envelope in five cities

表2列出了本研究中输入变量的变化范围，重点分析建筑外形改变导致的建筑能耗变化.办公建筑设定为矩形，所以第1个变量为矩形的长宽比；第2到第5个变量表示4个不同朝向建筑外墙的窗墙比；第6个变量是不同的楼层数，从1层到10层变化；第7个变量是建筑朝向变化，0.表示建筑朝向正北，然后其角度沿顺时针方向递增；最后一个变量表示建筑单层面积的变化，从1，000，m2到5，000，m2增加.动态能耗模拟模型基于美国能源部开发的能耗模拟软件EnergyPlus［11］.EnergyPlus程序经过了严格的验证，并已经得到广泛应用［4，7-8］.

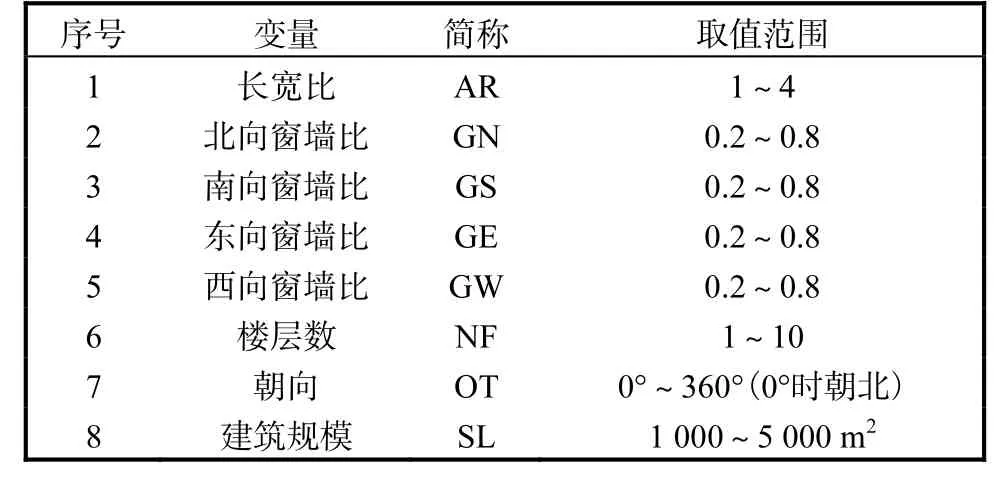
表2 建筑能耗模型中的变量Tab. 2 Variables used in building energy models

2 研究方法

2.1 机器学习方法

机器学习主要是研究人工智能领域中不同的计算机算法，目的是分析数据的特点以获取新知识或发现新规律等［12］.这种方法已经广泛用于不同的学科，在建筑能耗领域，主要是分析建筑能耗的特点，以建立可靠的建筑能耗预测模型.

本研究选取常见的6种机器学习方法（表3）.第1种方法是采用线形回归方法（linear regression）建立线形模型（linear model，LM）.其余5种方法是基于非参数回归方法，包括高斯过程（Gaussian process，GP）、多元自适应回归样条法（multivariate adaptive regression splines，MAS）、自助多元自适应回归样条法（bagging MARS，BMS）、随机森林（random forest，RF）和支持向量机（support vector machine，SVM）.高斯过程模型基于高斯随机过程和贝叶斯理论，适于处理小样本、非线性、多维数据等复杂问题，在机器学习领域得到广泛应用.多元自适应回归样条法是基于回归基函数的，其建模包括前向过程和后向过程两个主要步骤，前向过程加入基函数以提高模型拟合效果，后向过程则删除不必要项以避免模型过拟.自助多元自适应回归样条法是上一类模型的集成学习方法，通过对原始数据进行自助法抽样，产生很多新的训练集，利用多元自适应回归样条法生成相应的很多模型，最后使用平均所有模型预测的方法得到最终结果.这种自助法的主要优点是避免了单一模型预测时的不稳定性.随机森林法也属于集成学习方法，其基于分类回归树法，通过自助法随机选择向量产生大量的树模型，最后也是通过平均这些模型得到预测值.这种方法的优点是适用于变量数目非常大的场合，也可用于有相关自变量的问题.支持向量机基于核函数的小样本统计理论，确定不同类别之间的最优超平面，所以这种方法只是利用了有限的样本，可以避免过度拟合的问题，其中根据不同数据集的特点，核函数的选择多样包括线性、多项式、径向基等.关于6种方法的更多信息可以阅读文献［12-13］.

表3 6种机器学习方法Tab. 3 Six machine learning methods

需要强调的是，除了简单的线性模型外，大多数机器学习方法都可以调整至少1个参数，以提高模型的预测效果.例如随机森林法中树节点预选的变量个数，多元自适应回归样条法中剪枝个数和交互作用级数等都可以变化.在本文给定的机器学习方法中，每个可变化参数均有10个可能值，采用交叉验证法确定每个可能值时的模型预测效果，预测效果用均方根误差（root mean square error，RMSE）和决定系数（coefficient of determination，简写为R2）表示.

交叉验证法的基本思想是，将数据集等分为k组，首先选取第1组作为测试集，其余k-1组数据作为训练集以得到模型，所得模型利用第1组测试集评估模型预测效果；然后，选定第2组为测试集，其余k-1组为训练集；这个过程重复k遍，得到k个模型的预测效果值，取平均后得到这个模型的最终预测值.本研究中取k为10的情况，称为10折交叉验证法，也是机器学习方法中最常用的选择［13］.

均方根误差和决定系数是表达模型精度的常用统计量［12］.均方根误差可视作模型的平均误差，其优点是与输出变量有相同的单位.均方根误差越小，表明模型预测效果越好.决定系数是模型中变量可以解释的方差与总方差的比值，所以决定系数越大，表明模型精度越高.决定系数的取值位于0和1之间.

2.2 计算步骤

（1）确定机器学习方法中的变量及其变化范围（表2）.由于本研究是使变量在其变化范围内分布尽可能均匀，所以可取均匀分布.

（2）利用拉丁超立方（Latin hyper-cube）方法得到不同变量的组合，通常抽样次数至少为变量的10倍，本次研究选取100次以保证计算结果收敛.拉丁超立方抽样方法是一种在计算机仿真不确定性分析领域得到广泛使用的方法，其主要特点是保证抽样后的数据在空间内保持均匀性，并且不同变量可指定为不同的概率密度函数.

（3）利用R语言计算环境［14］生成EnergyPlus能耗模拟模型.R语言是免费的数据分析和可视化软件，具有非常强大的统计分析功能［14］.由于本次研究分为5个城市，每个城市需要建立100个模型，总共需500个能耗模型，不可能手动完成，所以利用R语言的文本编辑功能，自动完成能耗模型的生成.

（4）运行500个EnergyPlus模型，并用R语言收集计算结果.

（5）基于交叉验证方法选择机器学习方法中的参数，以确定其最优模型.最后，分析比较这些不同模型的建筑能耗预测效果.本文中的所有统计计算均在R语言环境［14］中完成.

3 结果与讨论

3.1 取暖能耗模型的比较

图2为在5个城市中6种机器学习方法用于建立取暖能耗模型时的准确性对比.图2（a）是根据均方根误差进行评估.通过交叉验证法得到的均方根误差越小，表明模型的预测精度越高.可以看出，根据自助多元自适应回归样条法建立的取暖能耗模型，在哈尔滨、上海和广州具有最高的准确度，而随机森林法在北京有最好的预测精度，多元自适应回归样条法更适合昆明地区.高斯过程和支持向量机有类似的精度，但与上述3种模型相比误差较大.线性模型在这6种模型中预测精度最差.综上所述，自助多元自适应回归样条法的模型在不同地区均有很好的效果，可以作为最优选择，多元自适应回归样条法和随机森林法作为辅助模型，以进一步确证取暖模型的预测效果.

图2（b）是依据决定系数所得的计算结果，可得出类似的结论.通过交叉验证法得到的决定系数越大，表明模型精度越高.3种最好的模型是自助多元自适应回归样条法、多元自适应回归样条法和随机森林法.

图25 个气候分区中办公建筑取暖能耗模型准确度对比Fig. 2Comparison of heating energy predicting accuracy by six machine learning methods in five cities

本文所采用的算法，不仅可以计算出不同能耗模型精度的点估计，而且能得到这些模型的不确定性分布.图3为将不同机器算法用于北京地区的采暖能耗模型的不确定性分布，图中圆点代表模型精度的中位数，变化区间表示95%，的可能变化范围.由图3可见，根据图2得到的3种性能较优的模型，包括多元自适应回归样条法、多元自适应回归样条法和随机森林法，不仅点估计值要好于其他3种性能较差的模型，而且其不确定性较小，进一步表明这3种模型非常适用于建立我国不同区域建筑的取暖能耗模型.

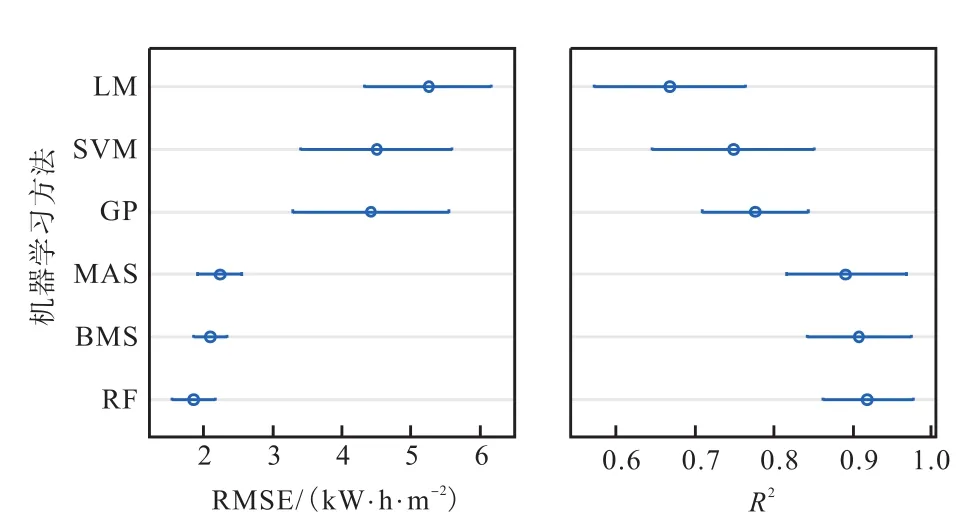
图3 北京地区6种机器学习方法的采暖能耗模型不确定性比较Fig. 3 Uncertainty of six machine learning approaches for predicting heating energy use in Beijing

3.2 制冷能耗模型的比较

图4给出在5个不同气候分区城市中6种机器学习方法用于预测制冷能耗时的精度对比.

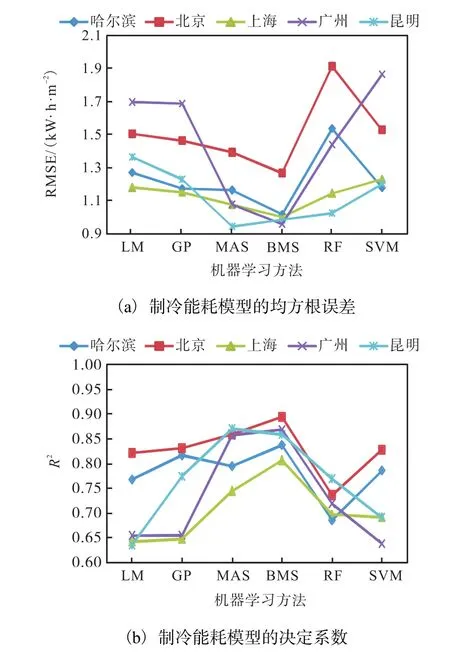
图4 5个气候分区中办公建筑制冷能耗模型准确度对比Fig. 4 Comparison of cooling energy predicting accuracy by six machine learning methods in five cities

6种方法预测制冷能耗时的均方根误差情况见图4（a），除了昆明外，其他4个城市中预测精度最高的都是基于自助多元自适应回归样条法所建立的模型.位于昆明的办公建筑，精度最好的是依据多元自适应回归样条法建立的模型，但与自助多元自适应回归样条法相比，误差相差较小.图4（b）为根据决定系数计算出的6种模型的准确度对比，与图4（a）得出的结论类似，自助多元自适应回归样条法是计算精度最好的机器学习方法.

由图4也可看出，基于高斯过程、随机森林和支持向量机的非参数回归模型，与简单的线性模型相比，预测精度相差较小，表明线性模型的预测能力并不一定低于复杂的非参数模型，这与Tian等［8］根据校园建筑能耗的研究结果一致.另外，由于线性模型具有更好的解释变量重要性及易于使用的优点，在建筑能耗研究中仍然具有重要的作用.

通过对比图2和图4可看出，取暖的决定系数要大于制冷的决定系数.特别是对于3种性能较优的模型（自助多元自适应回归样条法、多元自适应回归样条法和随机森林法），取暖模型的决定系数接近于1.这表明相比办公建筑中的取暖能耗，建筑外形与制冷能耗之间的相互关系要更加复杂，导致采用机器学习算法预测制冷能耗更加困难.由图2（b）和图4（b）还可发现，线性模型与本研究中表现最好的自助多元自适应回归样条法相比，取暖模型决定系数的提高比制冷模型要更加明显.这也表明办公建筑用于制冷时能耗变化的非线性关系要更加复杂.

图5给出广州地区6种机器学习方法用于制冷预测时模型精度95%，的变化区间.虽然不同机器学习方法的精度具有很多的相互重叠区域，但是多元自适应回归样条法及其自助法（自助多元自适应回归样条法）的性能明显优于其他4种机器学习方法.

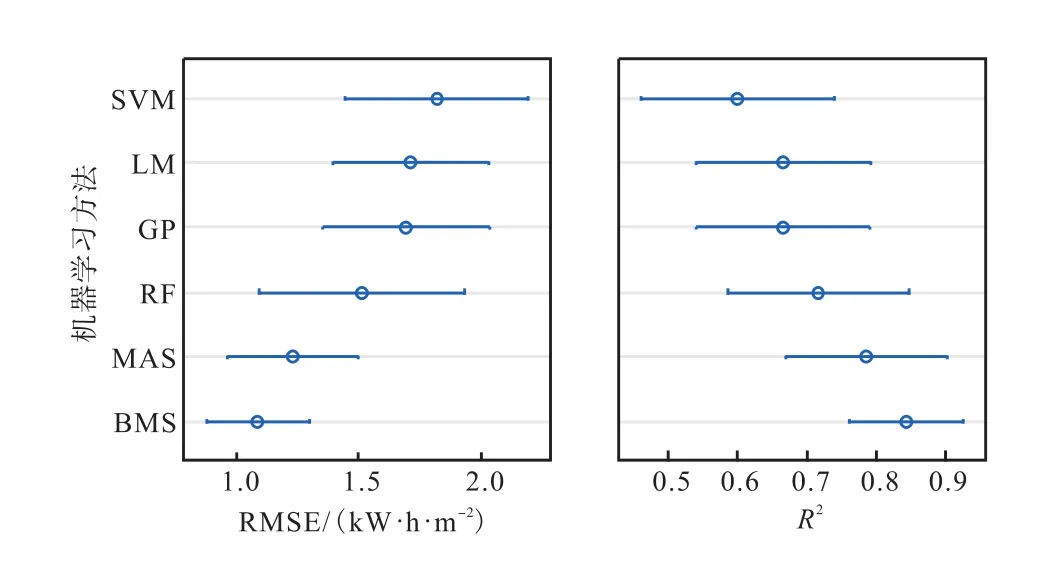
图5 广州地区6种机器学习方法的制冷能耗模型不确定性比较Fig. 5Uncertainty of six machine learning approaches for predicting cooling energy use in Guangzhou

根据研究得到性能最佳的机器学习模型，由于其计算速度快，一次模型运算时间小于1，s，非常适合于需要大量计算的能耗统计分析.例如，贝叶斯反演计算经常需要上万次的模型计算，使用工程EnergyPlus模型，对于复杂建筑的1次模型计算通常至少需要1，min，因此贝叶斯方法很难直接用于建筑能耗反演分析中，但采用本文得到的机器学习模型，则可方便快捷地应用贝叶斯方法进行模型反演分析.

4 结 论

（1）机器学习方法适用于建立建筑的取暖和制冷能耗模型，建立的模型计算速度快，适用于需要大量模型计算的研究中，如不确定性和敏感性分析、贝叶斯分析和最优化计算等.

（2）自助多元自适应回归样条法、多元自适应回归样条法和随机森林法这3种方法适于我国不同气候分区中建筑取暖能耗模型的预测中，计算精度高，而且误差区间较小.自助多元自适应回归样条法在不同气候分区的制冷能耗模型中有最好的计算精度.综合考虑取暖和制冷能耗，自助多元自适应回归样条法有最好的模型预测效果.需要说明的是，对其他类型的建筑，需要更多的研究确定此机器学习方法的适用性.

（3）与取暖能耗模型相比，制冷能耗与其影响因素之间有更加复杂的非线性关系，其模型预测要更困难.

［1］ 清华大学建筑节能研究中心. 中国建筑节能年度发展研究报告：2015［M］. 北京：中国建筑工业出版社，2015.

［2］ 张智超，李振亮，李亚，等. 链牵引式外遮阳百叶窗结构设计及其性能分析［J］. 天津科技大学学报，2013，28（6）：52-55.

［3］ 谢继红，乔木，陈东，等. 利用工质设计实现制冷热泵近卡诺循环的分析［J］. 天津科技大学学报，2006，21（1）：79-83.

［4］ Tian W. A review of sensitivity analysis methods in building energy analysis［J］. Renewable and Sustainable Energy Reviews，2013，20：411-420.

［5］ Capozzoli A，Grassi D，Causone F. Estimation models of heating energy consumption in schools for local authorities planning［J］. Energy and Buildings，2015，105：302-313.

［6］ Le K，Bourdais R，Gueguen H. From hybrid model predictive control to logical control for shading system：A support vector machine approach［J］. Energy and Buildings，2014，84：352-359.

［7］ Tian W，Choudhary R. A probabilistic energy model for non-domestic building sectors applied to analysis of school buildings in greater London［J］. Energy and Buildings，2012，54：1-11.

［8］ Tian W，Choudhary R，Augenbroe G，et al. Importance analysis and meta-model construction with correlated variables in evaluation of thermal performance of campus buildings［J］. Building and Environment，2015，92：61-74.

［9］ 中国气象局气象信息中心气象资料室，清华大学建筑技术科学系. 中国建筑热环境分析专用气象数据集［M］. 北京：中国建筑工业出版社，2005.

［10］ 中华人民共和国建设部，中华人民共和国国家质量监督检验检疫总局. GB 50189—2005 公共建筑节能设计标准［S］. 北京：中国建筑工业出版社，2005.

［11］ U. S. Department of Energy. EnergyPlus V8.3［R］. Washington：U. S. Department of Energy，2015.

［12］ Hastie T，Tibshirani R，Friedman J. The Elements of Statistical Learning：Data Mining，Inference，and Prediction［M］. 2nd ed. New York：Springer-Verlag，2009.

［13］ Kuhn M，Johnson K. Applied Predictive Modeling［M］. New York：Springer-Verlag，2013.

［14］ R Development Core Team. R：A language and environment for statistical computing［EB/OL］. ［2015-10-14］. http://www.R-project.org/.

责任编辑：常涛

Building Energy Models Based on Machine Learning Methods

TIAN Wei1，WEI Lai1，LI Zhanyong1，MENG Qingxin2，SONG Jitian1，YANG Song1
（1.Tianjin Key Laboratory of Integrated Design and On-line Monitoring for the Light Industry and Food Engineering Machinery and Equipment，College of Mechanical Engineering，Tianjin University of Science & Technology，Tianjin 300222，China；2.Logistics Group，Tianjin University of Science & Technology，Tianjin 300222，China）

This paper focuses on a comparison of predicting accuracy of six different machine learning approaches for estimating energy use in office buildings，including linear regression，GP（Gaussian process），MARS（multivariate adaptive regression splines），bagging MARS，RF（random forest） and SVM（support vector machine）.The results indicate that three methods（Bagging MARS，MARS，and RF）have better accuracy in predicting heating energy，whereas the bagging MARS performs best in estimating cooling energy.It is also found out that the prediction of cooling energy is more difficult than that of heating energy in office buildings.These conclusions can be used to provide some reference for machine learning method choosing in building energy assessment.Moreover，the models obtained from this research can also be used to create a building stock model at urban scales.

building energy saving；energy model；machine learning；model accuracy

TU17

A

1672-6510（2016）03-0054-06

10.13364/j.issn.1672-6510.20150158

2015-10-14；

2015-12-07

天津市应用基础与前沿技术研究计划资助项目（14JCYBJC42600）；教育部留学回国人员科研启动基金资助项目

田 玮（1975—），男，山西太谷人，教授，weitian@tust.edu.cn.

数字出版日期：2016-03-02；数字出版网址：http://www.cnki.net/kcms/detail/12.1355.N.20160302.1741.002.html.