间壁式单程换热器两侧流体温度分布的研究
2016-08-02晏丽红谢中华天津科技大学化工与材料学院天津300457天津科技大学理学院天津300457
晏丽红,谢中华(. 天津科技大学化工与材料学院,天津 300457;. 天津科技大学理学院,天津 300457)
间壁式单程换热器两侧流体温度分布的研究
晏丽红1,谢中华2
(1. 天津科技大学化工与材料学院,天津 300457;2. 天津科技大学理学院,天津 300457)
通过考察温度分布函数及其一阶导数和二阶导数,分析了3种情况下冷、热两种流体在间壁式单程换热器两侧的温度分布情况.结果表明:当两侧恒温时,温度分布线是平行于横轴的直线;一侧恒温一侧变温时,有温度变化流体的热容流量大小影响其温度分布线的单调性和凹凸性;当两侧变温且两种流体并流时,冷、热流体热容流量的大小影响温度分布线的单调性和凹凸性,热容流量的相对大小影响温度分布变化的相对快慢;当两侧变温且两种流体逆流时,冷、热流体热容流量的大小影响温度分布线的单调性,热容流量的相对大小影响温度分布线的凹凸性和变化的相对快慢.
间壁式单程换热器;温度分布;冷流体;热流体;热容流量
传热学是化工原理课程的主要内容之一,间壁式单程换热器又是传热学中重点讲授的换热设备类型.在介绍冷、热两种流体在间壁式单程换热器两侧的总传热过程时,需推导两种流体在整个换热器上的平均温差,因此要分析冷、热流体在间壁两侧的温度分布情况,但是在大部分的传热学[1]和化工原理[2]教材中只是粗略画出了温度分布曲线,并未深入探讨这些温度分布曲线的单调性和凹凸性.一些文献[3-8]研究了两种流体在间壁两侧的温度沿程变化,但只考虑了两侧变温的情况.本文通过考察冷、热流体的温度分布函数及其一阶导数和二阶导数,讨论两侧均恒温、一侧恒温一侧变温和两侧均变温3种情况下冷、热两种流体在间壁两侧的温度变化,分析影响温度分布曲线形状的因素,总结温度分布的规律.
1 研究方法
本文采用微分方法来推导两种流体的温度分布函数.推导过程中,忽略换热器的热量损失.以换热器的换热面积A作为自变量,并以热流体的流动方向作为换热面积A的正方向,冷、热流体的温度作为因变量,在换热器上任取一个微元换热面积dA.

首先,在dA上列出微分传热速率方程再分别列出热、冷流体有温度变化时的微分热量衡算方程:
热流体放出的热量

式中:ms1、ms2分别为热、冷流体的质量流量,kgs;cp1、cp2分别为热、冷流体的平均比定压热容,kJ/(kg⋅℃);T、t分别为热、冷流体在dA处的温度,℃;Q为总传热速率,W;K为换热器的平均总传热系数,W/(m2⋅℃);A为换热器的传热面积,m2.
由式(1)和式(2)得到热流体温度变化的微分式

由式(1)和式(3)得到并流时冷流体温度变化的微分式

由式(1)和式(4)得到逆流时冷流体温度变化的微分式

联立上述微分方程,解出冷、热流体的温度沿程分布方程;再求出温度分布函数的一阶导数和二阶导数,以确定温度分布曲线的单调性和凹凸性.
2 不同情况的分析方法
2.1 两侧均恒温
在蒸发器和再沸器中,热流体是饱和水蒸气,冷流体是饱和液体,则饱和水蒸气在间壁一侧冷凝,饱和液体在另一侧沸腾,两种流体的温度均不变.
2.2 一侧恒温,一侧变温
当一种流体在饱和状态下于间壁式换热器的一侧发生相变,另一种流体在另一侧升温或降温,则这种情况属于一侧恒温一侧变温.
2.2.1 一侧是热流体为饱和蒸气冷凝,另一侧是冷流体被加热
当发生相变的流体是饱和蒸气,例如用饱和水蒸气加热某种流体,则饱和蒸气冷凝成饱和液体并在饱和温度下排出;因此热流体温度不变,冷流体被加热,温度升高.
当冷流体与热流体并流时,冷流体的温度变化分析如下.
将式(6)分离变量得
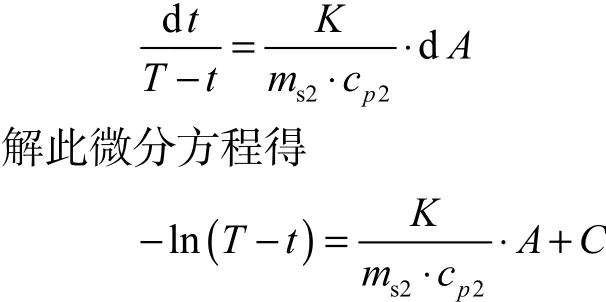
式中:C为常数.初始条件为:A=0,t=t1(t1为冷流体进口温度).代入上式并整理得
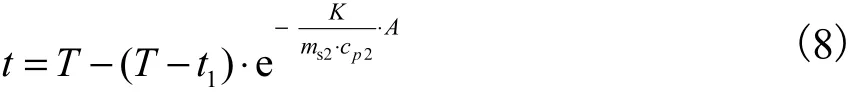
式(8)即冷流体的温度沿程分布函数.若要进一步分析温度分布线的单调性和凹凸性,则需对此方程求一阶导数和二阶导数.
对式(8)求一阶导数得
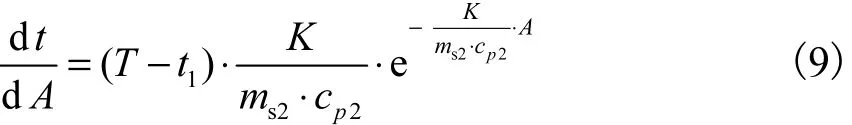
由此可知冷流体的温度沿着换热器的变化是单增的.
对式(8)求二阶导数得
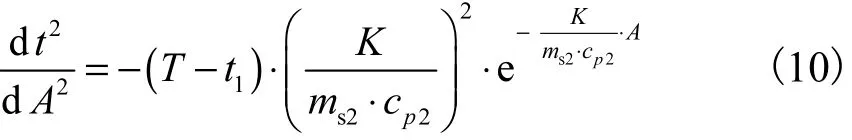
由此可知此条温度分布线是向上凸的.
当冷流体与热流体逆流时,同理可得冷流体的温度分布函数及其一阶导数和二阶导数.
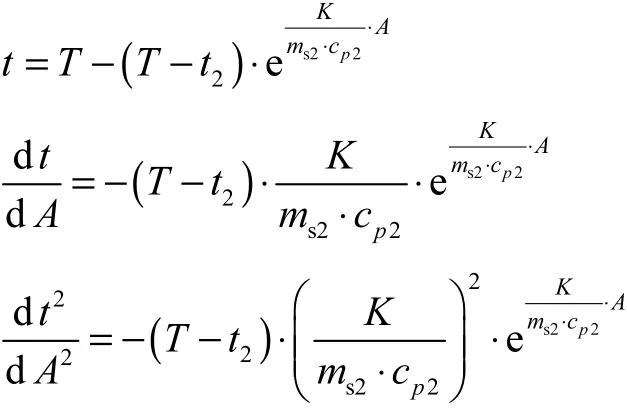
2.2.2 一侧是冷流体为饱和液体沸腾,另一侧是热流体被冷却
当发生相变的流体是饱和液体,则饱和液体在换热器的一侧沸腾成为饱和蒸气,温度不变;无论逆流还是并流,温度分布线都是平行于横轴的直线.另一侧热流体温度降低.热流体的温度分布分析如下.
将式(5)分离变量,解微分方程并代入初始条件,得到热流体的温度分布函数

式中:t为冷流体的温度,℃;1T为热流体在换热器进口处的温度,℃.一阶导数为

因此,热流体的温度分布曲线是单调减小并向下凹的.
2.3 两侧均变温
当间壁式两侧的流体均不发生相变,而是被加热或被冷却,则两种流体的温度都随着换热器变化,本文分别讨论两种流体并流和逆流的情况.
2.3.1 两种流体并流
由式(2)和式(3)可得


式中:1tΔ为热流体入口侧热冷流体的温差.
式(15)即温差分布函数,对此函数求一阶导数得
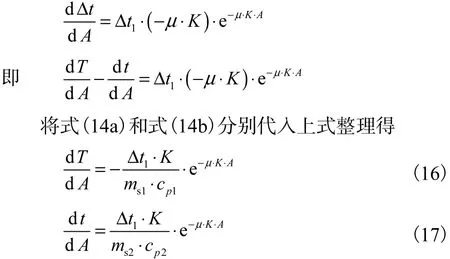
分别解式(16)和式(17)这两个微分方程,并将初始条件代入,得到热、冷流体的温度沿程分布函数

2.3.2 两种流体逆流
先讨论冷、热流体的热容流量相等,即ms1⋅cp1=ms2⋅cp2的情况.据式(5)和式(7)知,此时dT=dt即d(T−t)=0,两条温度分布线之间的垂直距离处处相等,则T−t=Δt1,则式(5)和式(7)可分别表示为
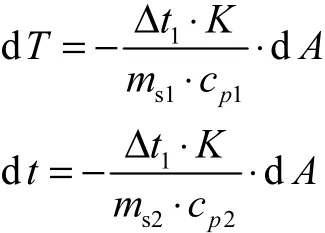
分别解上述2个微分方程,并将初始条件代入,可得
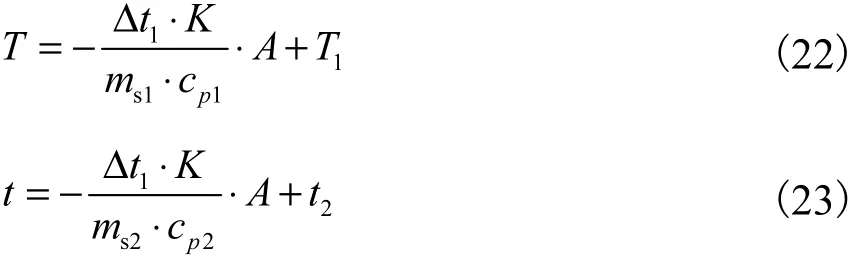
可看出冷、热流体的温度分布线均为直线,且斜率相等,故不必再求一阶和二阶导数.
再讨论冷、热流体的热容流量不相等,即ms1⋅cp1≠ms2⋅cp2时的情况.

解上述微分方程并把初始条件代入并整理得

式(25)即温差沿程分布函数,求此函数的一阶导数
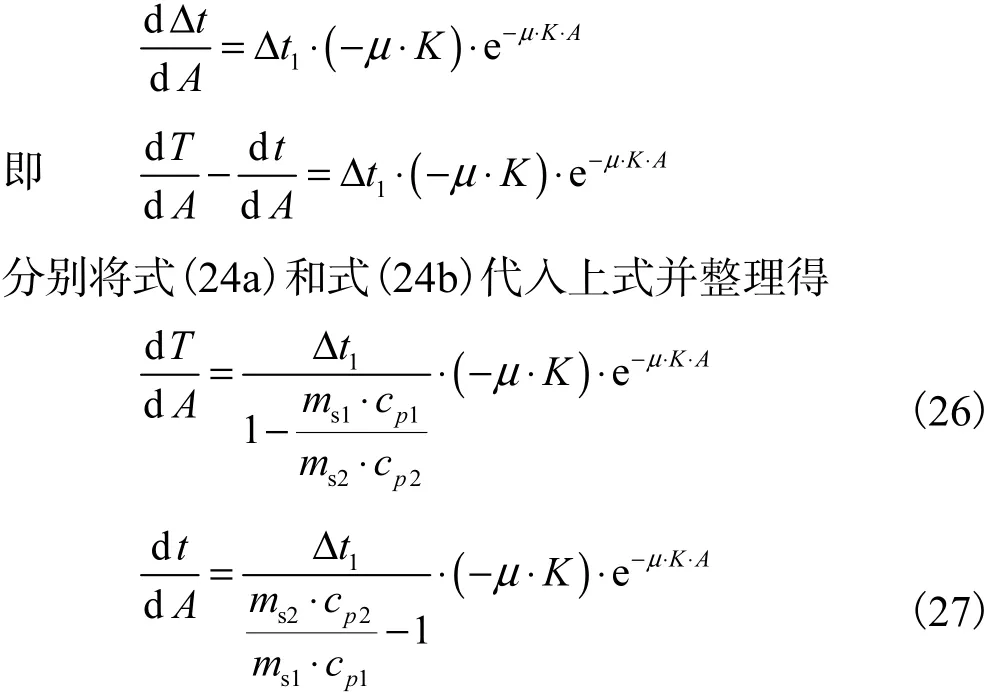
解上述微分方程并把初始条件代入,得热、冷流体的温度沿程分布函数

再对式(26)和式(27)分别求二阶导数得
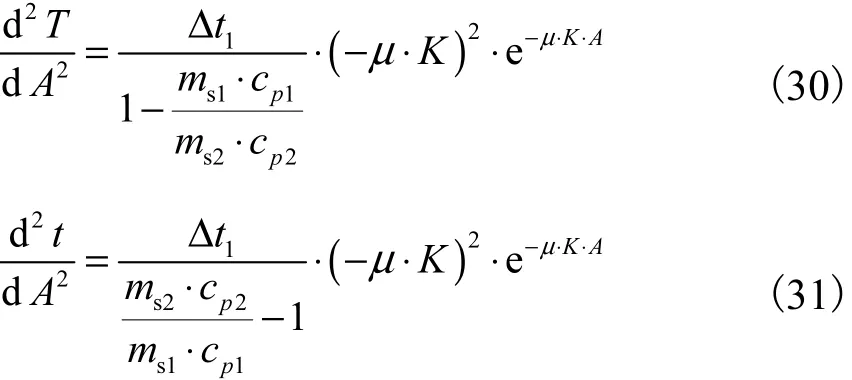
3 结果与讨论
3.1 两侧恒温时的温度分布
这种情况下冷、热流体的温度分布线最简单,是两条与横轴平行的直线(见图1),即温度分布与两种流体的流向和热容流量的相对大小无关.
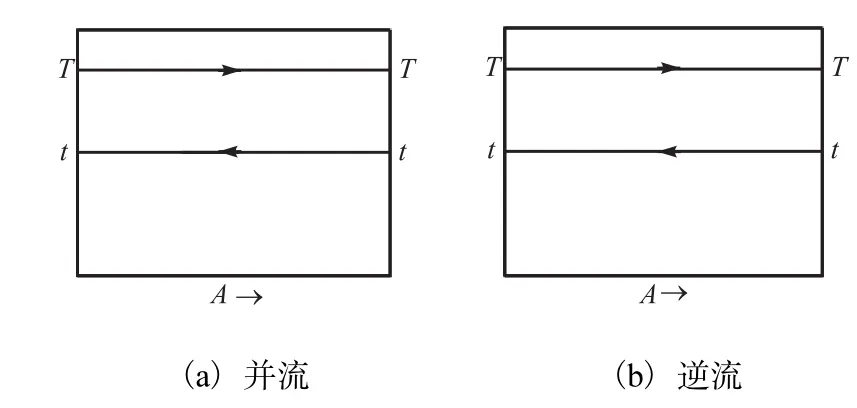
图1 两侧恒温的温度分布Fig. 1Temperature profile for constant temperatures inside and outside heat exchanges
3.2 一侧恒温一侧变温时的温度分布
一侧恒温一侧变温时,有温度变化的流体的温度分布曲线形状只由该种流体的热容流量的大小决定.一侧恒温一侧变温情况下的温度沿程变化情况见表1.
3.3 两侧变温时温度分布
3.3.1 并流
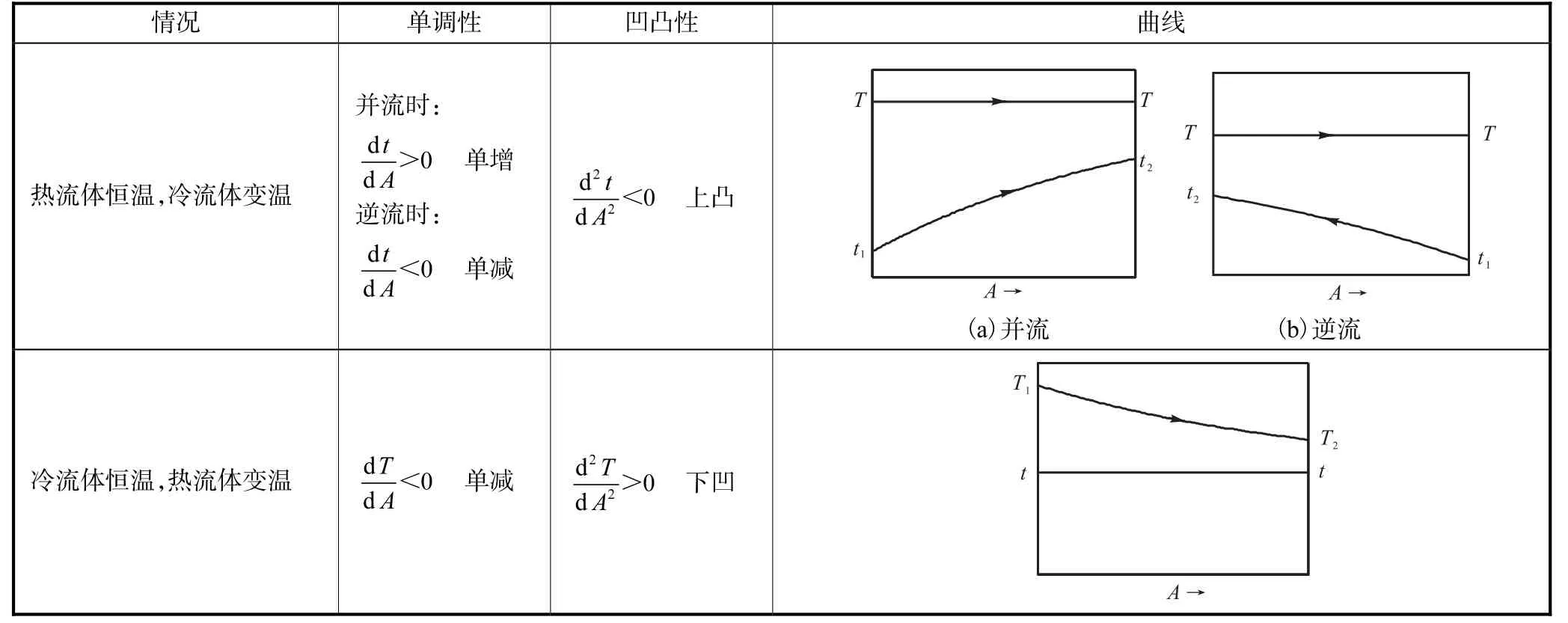
表1 一侧恒温一侧变温冷热流体的温度变化情况Tab. 1 Temperature profile for variable temperatures
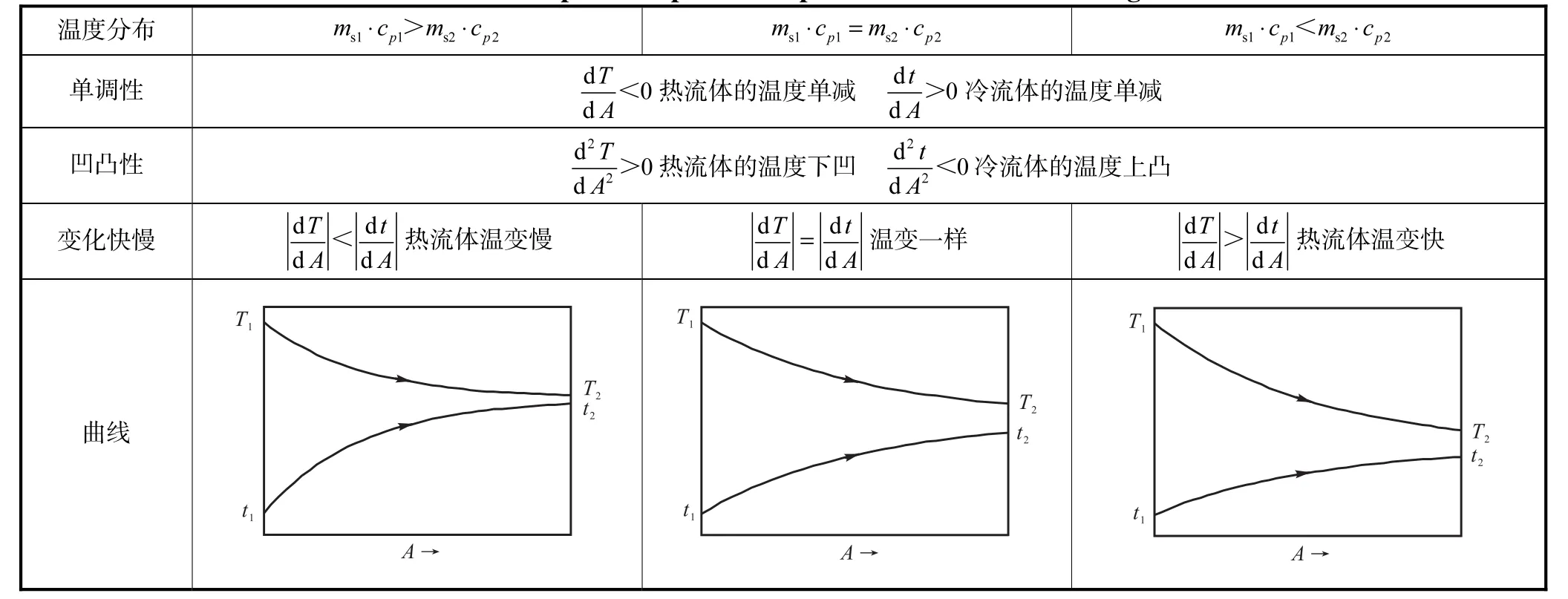
表2 两侧变温并流时两种流体的温度沿程分布Tab. 2 Temperature profile for parallel flow in heat exchanges
3.3.2 逆流
由前推导可知,逆流时冷、热流体的温度分布的单调性由该种流体的热容流量的大小决定,两个温度分布函数的一阶导数均小于0,故两条温度曲线都是单调减小的.
冷、热流体温度分布线的凹凸性和变化快慢由两种流体热容流量的相对大小决定:当ms1⋅cp1=ms2⋅cp2时,两个温度分布函数的一阶导数相等且二阶导数为0,说明两条温度变化线是斜率相等且为负值的直线;当ms1⋅cp1>ms2⋅cp2,两个温度分布函数二阶导数小于0,说明两条曲线是向上凸的,并且由于所以热流体的温度变化要比冷流体慢;当ms1⋅cp1<ms2⋅cp2,两个温度分布函数的二阶导数大于0,说明两条温度变化曲线是向下凹的,并且由于,所以热流体的温度变化比冷流体快.逆流时两种流体的温度沿程分布见表3.
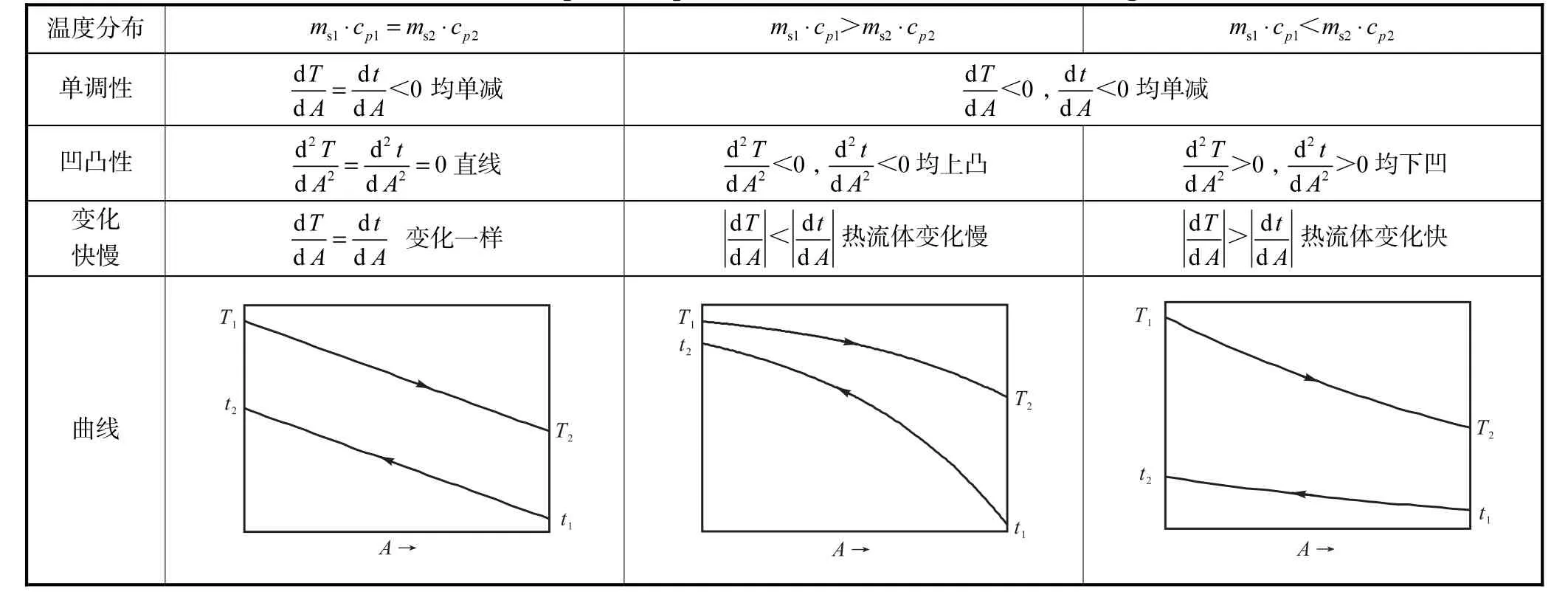
表3 两侧变温逆流时两种流体的温度沿程分布Tab. 3 Temperature profile for counter flow in heat exchanges
4 结 论
影响单程型间壁式换热器两侧流体的温度沿程分布的主要因素有两种流体的流向、两种流体的热容流量的大小以及相对大小.
(1)当两侧恒温时,温度分布线是平行于横轴的直线.
(2)当一侧恒温一侧变温时,恒温的流体温度分布线是平行于横轴的直线,有温度变化的流体温度分布线的形状只受该种流体的热容流量大小的影响.
(3)当两侧变温且两种流体并流时,冷、热流体的热容流量的大小影响温度分布线的单调性和凹凸性,热流体温度分布线总是单减下凹,冷流体温度分布线总是单增上凸.热容流量的相对大小影响两条温度分布线变化的相对快慢:当ms1⋅cp1=ms2⋅cp2时,二者变化速率一样;当ms1⋅cp1>ms2⋅cp2,热流体的温度变化比冷流体慢;当ms1⋅cp1<ms2⋅cp2时,热流体的温度变化比冷流体快.
当两侧变温且两种流体逆流时,冷、热流体的热容流量的大小影响两条温度分布线的单调性,两条温度分布线总是单减.热容流量的相对大小影响温度分布线的凹凸性和变化的相对快慢:当ms1⋅cp1=ms2⋅cp2,两条温度分布线是斜率相等的直线,二者变化速率一样;当ms1⋅cp1>ms2⋅cp2时,两条温度分布线均上凸,且热流体的温度变化比冷流体慢;当ms1⋅cp1<ms2⋅cp2,两条温度分布线均下凹,且热流体的温度变化比冷流体快.
[1] 杨世铭,陶文铨. 传热学[M]. 4版. 北京:高等教育出版社,2006.
[2] 谭天恩,窦梅. 化工原理:上册[M]. 4版. 北京:化学工业出版社,2013.
[3] 许光映. 顺逆流换热器部分冷热流体温度凸凹变化的数学解析[J]. 浙江海洋学院学报:自然科学版,2009,28(2):133-136.
[4] 雷筱芬. 单程换热器流体温度沿程分布函数[J]. 南昌大学学报:理科版,2007,31(6):583-585.
[5] 梁日忠. 间壁换热器流体的温度分布[J]. 化学工业与工程技术,2000,21(3):1-4.
[6] 李铭新,李振强,陈密. 热交换器温度曲线形状[J]. 吉林化工学院学报,1996,13(3):20-23.
[7] 陶金连. 顺、逆流换热器温度分布曲线的形状分析[J].安徽工学院学报,1993,12(1):92-96.
[8] 黄文瀛. 间壁式换热器逆流或并流时载热体温度的沿程分布[J]. 江西工业大学学报,1986,8(2):40-46.
责任编辑:周建军
Temperature Profile of Wall-type Heat Exchangers with Single Pass
YAN Lihong1,XIE Zhonghua2
(1.College of Chemical Engineering and Materials Science,Tianjin University of Science & Technology,Tianjin 300457,China;2.College of Science,Tianjin University of Science & Technology,Tianjin 300457,China)
Three cases of temperature profile of cold and hot fluids in wall-type heat exchangers with single pass were analyzed by considering temperature distribution functions, their first derivatives and second derivatives. The results show that the temperature profile is of two lines parallel to the horizontal axis when the temperatures of two fluids on the two sides of heat exchangers are constant. The monotonicity, concavity and convexity of temperature profile are influenced by the specific heat capacity flow rate value of the fluidof different temperature when the temperature of one fluid is constant and the temperature of the other fluid is varied. The monotonicity, concavity and convexity of temperature profile for parallel flow in heat exchanges are influenced by the specific heat capacity flow rate values of two fluids. The relative speed of temperature change is influenced by the specific heat capacity flow rate relative values of two fluids when the temperatures of two fluids are variables. The monotonicity of temperature profile for counter flow in heat exchanges is influenced by the specific heat capacity flow rate values of two fluids. The concavity and convexity of temperature profile and the relative speed of temperature changes are influenced by the specific heat capacity flow rate relative values of two fluids when the temperatures of two fluids are variables.
wall-type heat exchanger with single pass;temperature profile;cold fluid;hot fluid;specific capacity flow rate
TQ021.3
A
1672-6510(2016)03-0048-06
10.13364/j.issn.1672-6510.20150247
2015-12-15;
2016-01-18
晏丽红(1977—),女,山西人,讲师,yanlih@tust.edu.cn.
