三步法求解下层最优解不唯一的二层规划

王　剑　胡铁松　汪　琴

(武汉大学 水资源与水电工程科学国家重点实验室， 武汉　430072)



三步法求解下层最优解不唯一的二层规划

王剑胡铁松汪琴

(武汉大学 水资源与水电工程科学国家重点实验室， 武汉430072)

摘要：下层最优解不唯一的二层规划存在乐观和悲观情形，基于此提出乐观和悲观可行解的定义，并设计了求解乐观和悲观最优解的三步法．而后分别用三步法和以往的两步法求解了4个下层最优解不唯一和1个下层最优解唯一的算例，计算结果表明了三步法的有效性．

关键词：二层规划；乐观最优解；悲观最优解

二层规划可行上层决策对应的下层规划问题最优解数目通常并非唯一，二层规划的下层问题具有唯一解是一类特殊二层规划问题，只有当对应下层规划为凸规划且目标函数为严格凸函数时，其最优解才唯一[1]．下层规划最优解不唯一的二层规划的求解难点在于：对于一个可行的上层决策变量，其对应下层最优解的数目难以确定，目前尚缺乏一种解法可以求解出下层问题的所有最优解并将其反馈到上层规划．因此，研究与探讨下层最优解不唯一的二层规划问题具有重要价值．

下层最优解不唯一的二层规划的最优解尚无一个公认的定义，Lucchetti R, Mignanego F等[2]提出了三个定义，其中第一条和第二条定义分别对应Dempe[3]提到的乐观和悲观形式二层规划的最优解，也是较为通用的解定义，而第三条定义条件非常严苛，因而使用得极少．另外有一些学者，通过对原二层规划问题进行处理，使得下层问题最优解唯一．Bialas和Karwan[4]提出在下层决策者配合上层决策者时，用f2+εf1来代替下层目标函数f2，其中f1为上层目标函数，ε为一个适当小的正数；相应地Ben-Ayed O[5]提出在下层决策者不配合上层决策者时，用f2-εf1来代替下层目标函数f2．但两者只是提出了一种思路，并没有指出ε应当如何选取，并且即使在替换了下层目标函数以后，也不能保证下层最优解唯一．Dempe则提出了两种正则化方法对原二层规划进行扰动，第一种[6]是针对乐观情形，在下层目标函数为凸函数，且上层目标函数正定的情况下，在下层目标函数中添加αF，α为一个适当小的正数，并用梯度法进行求解；第二种[7]是在下层规划为凸规划时，在目标函数中添加α‖x‖，并用聚束法进行求解．相类似地，P.Loridan和J.Morgan针对下层问题严格拟凸与否，提出了两种ε-正则法[8-9]，并讨论了一定条件下解的存在问题，也提出了几个较为简单的算法．但不论是Dempe还是P.Loridan和J.Morgan提出的方法都存在两个问题：第一，对下层问题有一定的要求，针对的是较为简单的二层规划问题，提出的方法难以解决一个一般的下层最优解不唯一的二层规划问题；第二，改变了原二层规划问题，并不能保证最后求得的解满足下层问题的最优性．

近年来有一类解法，上下层都采用启发式算法进行求解，因为该类算法使用了两次启发式算法，可以归类为两步法，如基于遗传算法的[10]，基于粒子群算法的[11]等．但用两步法求解下层最优解不唯一的二层规划，下层规划将随机返回一个最优解到上层，因而算法结果将不稳定，无法保证求得乐观最优解或者悲观最优解．

本文从乐观和悲观二层规划的定义出发，提出乐观和悲观可行解的定义，分析了这两类可行解的求解思路，而后设计了三步法求解下层最优解不唯一的二层规划的乐观和悲观最优解．下文将按照如下顺序展开：第1部分描述二层规划的相关数学定义及乐观和悲观最优解，第2部分提出乐观和悲观可行解的定义和求解乐观和悲观最优解的三步法，第3部分是算例及结果分析，第4部分是结论和未来工作．

1二层规划的两类最优解

考虑如下形式的二层规划问题(记为问题1)：

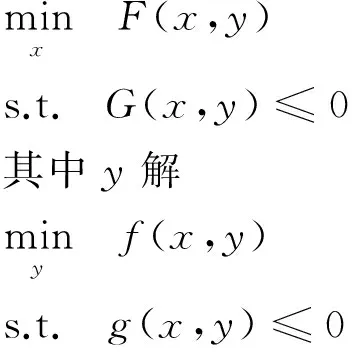
(1)

其中x∈Rn1，y∈Rn2，F，f：Rn1×Rn2→R，G：Rn1×Rn2→Rm1，g：Rn1×Rn2→Rm2.

1)约束域：

上下层约束条件的交集称为约束域A，即：A={(x，y)|G(x，y)≤0，g(x，y)≤0}.

2)可行上层决策变量：

将满足x∈A的上层决策变量x称为可行上层决策变量，所有的可行上层决策变量的集合用X表示，它表示约束域A在上层决策空间的投影，即：X={x|(x，y)∈A}.

3)反应集：

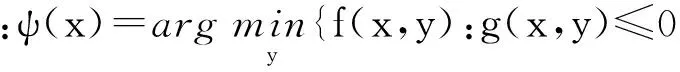
当二层规划的可行上层决策变量x，对应的下层问题的最优解并非唯一时，下层问题返回的最优解具有不确定性．此时，有两种决策方式，相应地有两类最优解．

1.1乐观最优解

乐观决策者认为下层完全配合上层目标，总是将对上层目标最有利的最优解返回给上层，这种情况下的二层规划称为乐观二层规划，得到的最优解即为乐观最优解．

乐观二层规划的数学表达[3]：

(2)

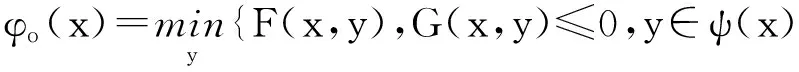
1.2悲观最优解

P.Loridan和J.Morgan[12]提出在下层决策者不配合上层决策者时，上层决策者为了使得风险最小，认为下层决策者总是选择最不利于上层的最优解，这种情形下的二层规划称为悲观二层规划，得到的最优解即为悲观最优解．

悲观二层规划的数学表达[3]：

(4)

2三步法求解乐观和悲观最优解

2.1等价约束

对于任意一个固定的上层决策变量x，如果下层问题存在最优解，那么下层问题一定存在唯一的最优值f*，显然，对于任意一个x′∈X有：{y|f(x′，y)=f*}={y|y∈ψ(x′)}．

2.2乐观可行解

根据乐观二层规划的定义，对于一个x′∈X，当y是如下问题o的最优解时，这个y才会被乐观上层决策者接受，从而(x′，y)才是乐观二层规划的一个可行解，称为乐观可行解．

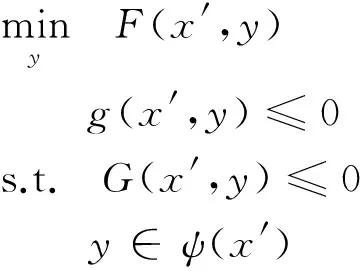
(7)

由于ψ(x′)数目无法确定，也无法全部求出，故用f(x′，y)=f*代替y∈ψ(x′)可以得到问题o的等价问题3：

(8)

2.3悲观可行解

同理，根据悲观二层规划的定义，对于一个x′∈X，当y是如下问题p的最优解时，(x′，y)是悲观二层规划的一个可行解，称为悲观可行解．

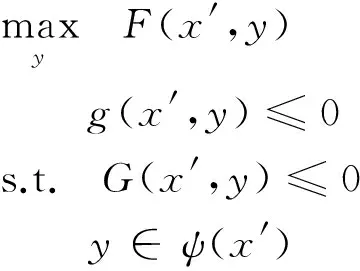
(9)

与乐观可行解求解类似，可以得到问题p的等价问题4：

(10)

2.4乐观&悲观可行解求解

根据上文的分析，可以通过如下3个步骤求解乐观和悲观可行解：第1步，确定一个满足x′∈X的x′；第2步，求解x′对应下层规划问题2的最优值f*；第3步，求解x′对应的问题3(4)，得到最优解y，最终得到一个乐观(悲观)可行解(x′，y)．

2.5三步法求解乐观&悲观最优解

上文给出了求解单个乐观(悲观)可行解的方法，如果使上层决策变量在X内变化，并求解对应的乐观(悲观)可行解，最后比较这些乐观(悲观)可行解的适应度(上层目标函数值)大小，适应度最小的乐观(悲观)可行解就是原二层规划问题的乐观(悲观)最优解，具体过程如图1所示．

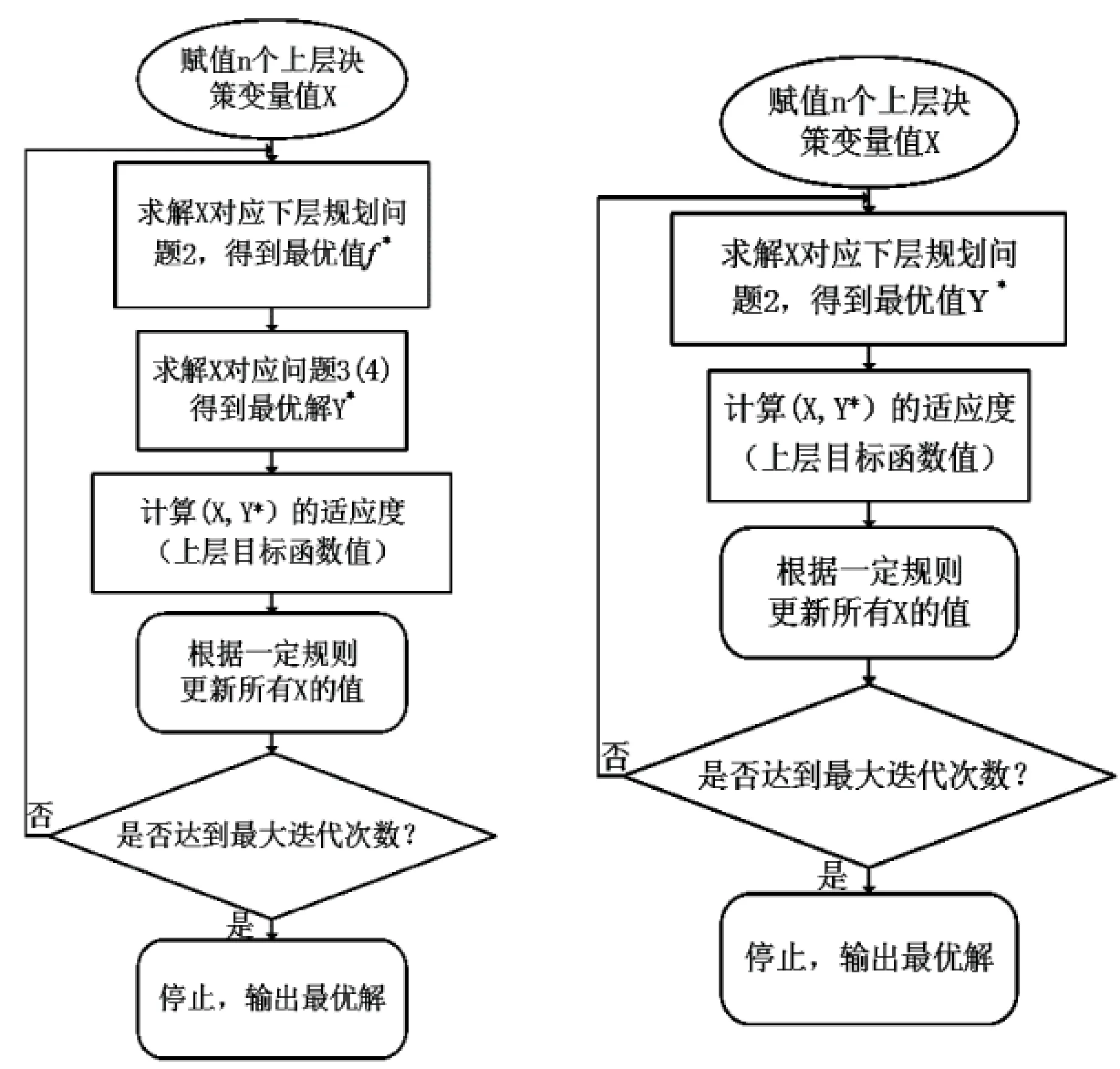
图1　三步法运行过程　　　　图2　两步法迭代过程

2.6三步法和两步法对比

新方法是一个求解策略，并不针对某一种特定的算法，为了使得算法适用性更广，可以采用启发式算法和新方法结合．新方法总共使用了3次启发式算法，故而命名为三步法．为了方便对比，将两步法的流程列入图2，可以看出三步法和两步法差别就在于是否有问题3(4)的求解，且两步法在下层问题完成求解后直接返回了下层最优解Y*，三步法返回的是下层最优值f*，再经过问题3(4)的求解返回Y*．

3算例及结果

为了验证新方法的有效性，下面分别用基于粒子群的两步法和三步法对5个算例进行求解．算例1，2，3节选自文献，算例4，5为作者构造算例；算例1，2，4，5下层最优解不唯一，算例3下层最优解唯一；算例4，5决策变量维数可变，计算时算例4包括1+2和2+3维，算例5包括2+2维和4+4维．为了方便对比，三步法和两步法的问题1和问题2的的粒子数和迭代次数均相同．

算例1[3]：

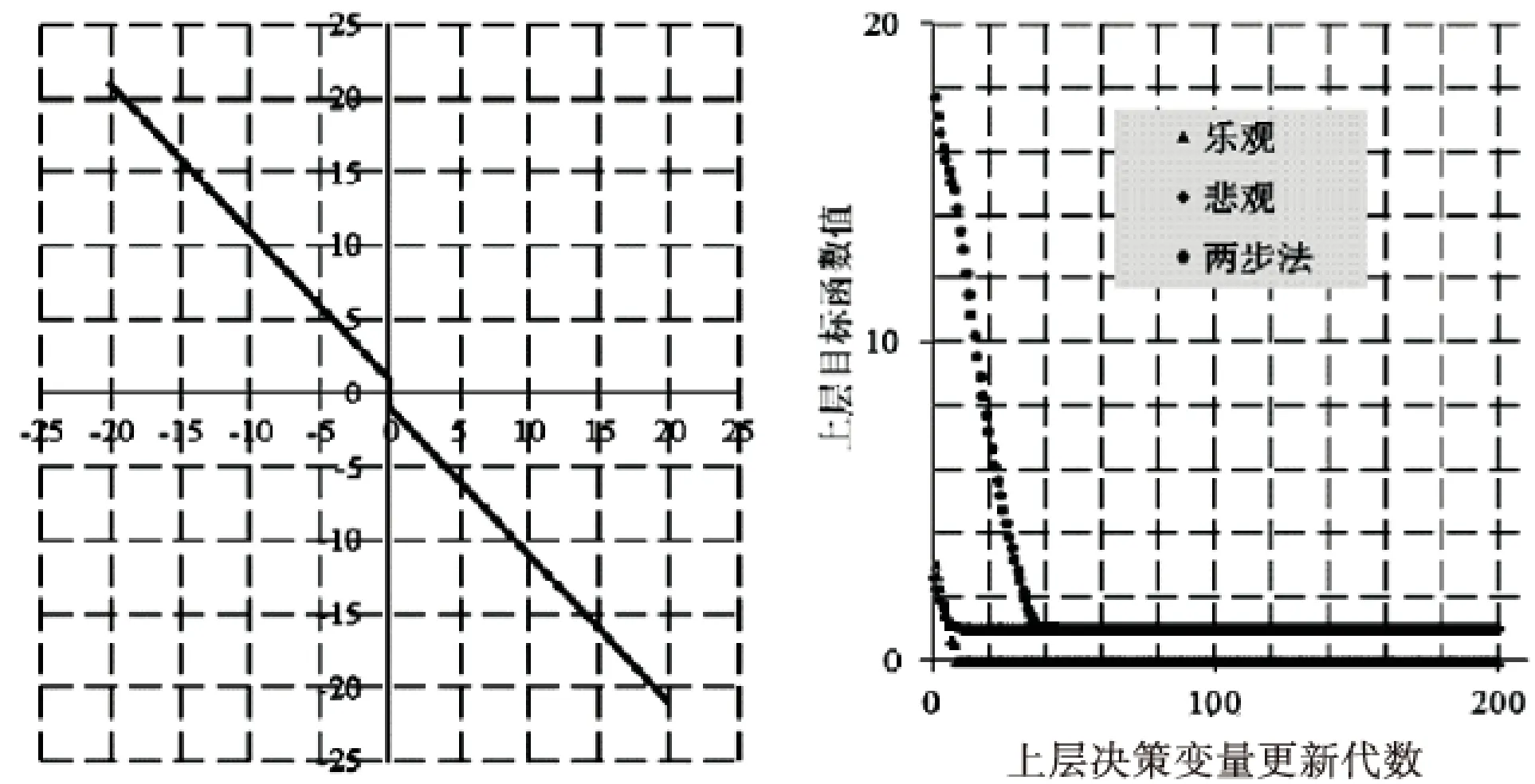
图3　算例1可行域　　　　图4　算例1迭代过程

3种迭代都进行了多次计算，乐观和悲观迭代过程不尽相同，但收敛结果一致，上图只是选取了其中一次；两步法的迭代过程不尽相同，迭代也不一样，上图也只是选取了其中一次(下文算例同)．乐观过程收敛代数为51，收敛最优解为(-1.62e-23，2.22e-24)，最优值为0；悲观过程收敛代数为176，收敛最优解为(2.66e-04，1.003 11)，最优值为1.000 091；两步法收敛代数为146代，收敛最优解为(4.02e-09，-1)，最优值为1．三步法顺利求解了乐观最优解和悲观最优解，而两步法也刚好求解出了悲观最优解，这是一个特例．

算例2[2]：

算例2反应集为：ψ(x)={(y1，y2)|y1+y2=1，x+y1-y2≤1，0≤x≤2}，可行域如图5所示，任意一个x对应下层规划有无穷多个最优解．

乐观最优解为：(x*，y*)=(0，1)，对应乐观最优值为1 000；悲观最优解为：(x*，y*)=(2，0)，对应悲观最优值为200．三步法和两步法的迭代过程如图6所示．

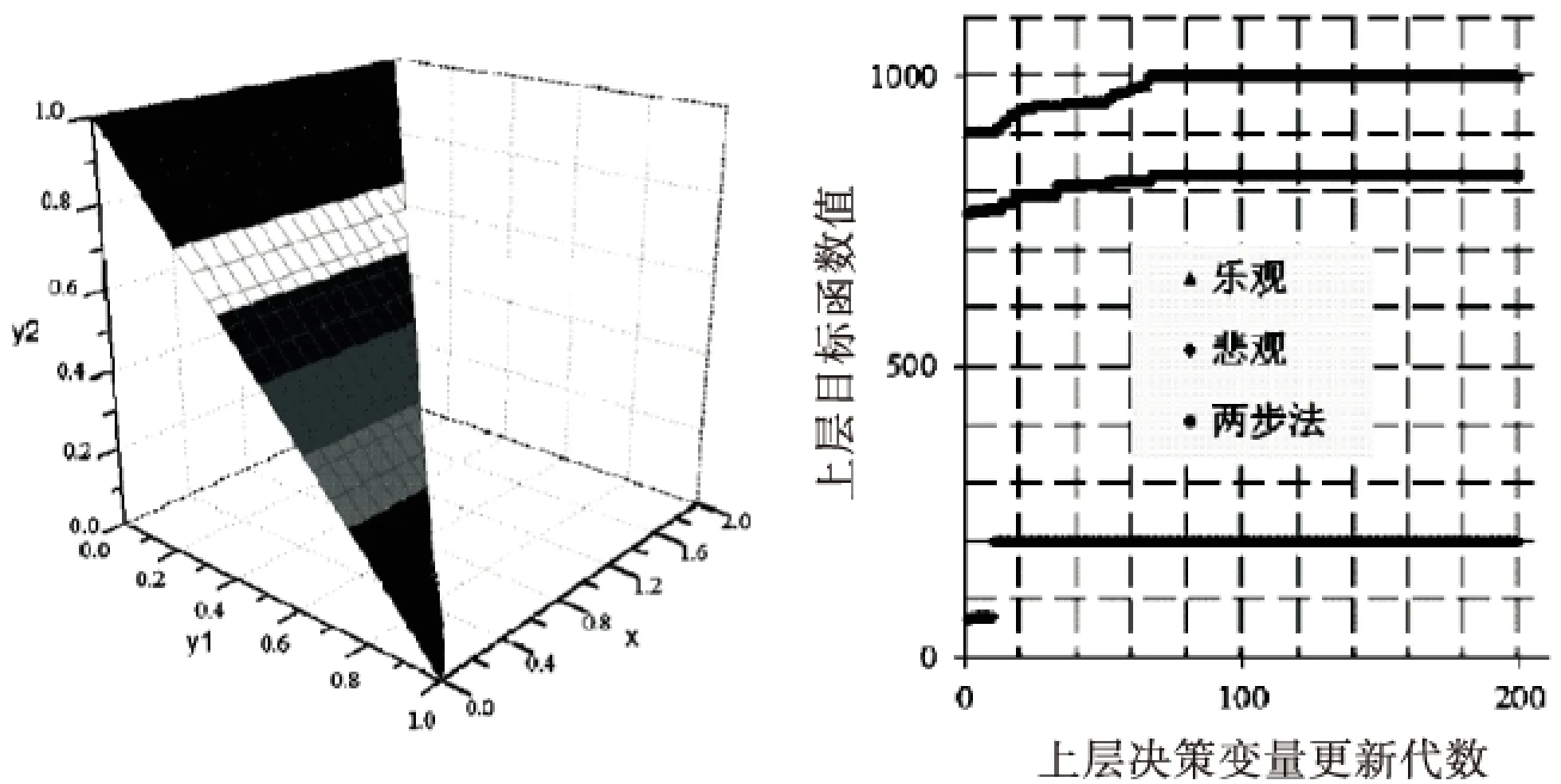
图5　例2可行域　　　　　　图6　例2迭代过程

乐观过程收敛代数为130，收敛最优解为(-1.56e-03，1.001 06，-5.04e-04)，最优值为1 000.870；悲观过程收敛代数为126，收敛最优解为(2.000 03，-2.94e-04，1.003 45)，最优值为199.699 6；两步法收敛代数为68代，收敛最优解为(0.203 076 1，0.895 614 0，0.104 396)，最优值为829.162 5．三步法分别求解了乐观最优解和悲观最优解，而两步法求解不了乐观最优解和悲观最优解的任意一种．

算例3[13]：

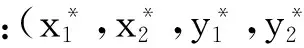
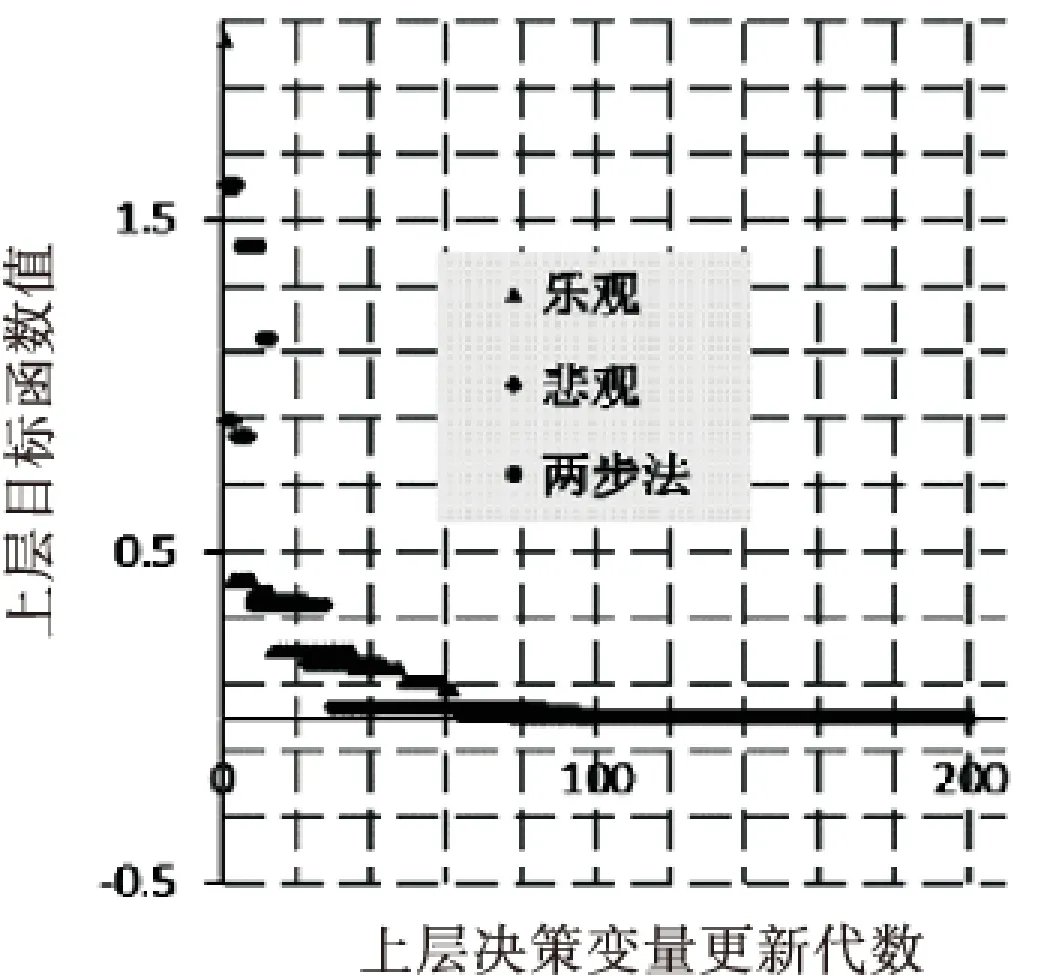
图7　算例3迭代过程

乐观过程收敛代数为200，收敛最优解为(-1.11e-03，29.995 2，-10.000 1，9.997 54)，最优值为-2.934e-03；悲观过程收敛代数为198，收敛最优解为(-1.18e-03，29.995 5，-10.000 1，9.997 66)，最优值为-2.658e-03；两步法收敛代数为149代，收敛最优解为(-1.07e-03，29.995 2，-10.000 1，9.997 56)，最优值为-3.038e-03．3种迭代过程大同小异，收敛的最优解和最优值都较为接近，3种迭代运算应该还有继续收敛到更优解的可能，但最优解和最优解的精度已经很高．

算例4：

s.t.0≤xi≤4

yj≥0

算例4的反应集为：

对于任意一个可行上层决策变量，下层最优解均为无穷多个．乐观最优解为：

乐观最优值为0，悲观最优解为：

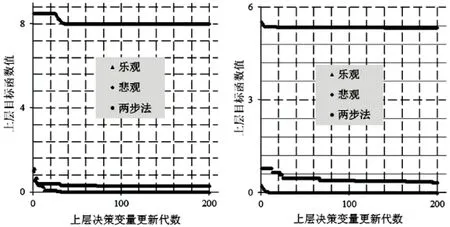
图8　算例4迭代过程(左边1+2维，右边2+3维)

对于1+2维：乐观过程收敛代数为105，收敛最优解为(0，4.88e-04，4)，最优值为2.387e-04；悲观过程收敛代数为39，收敛最优解为(2.001 68，1.998 83，3.08e-08)，最优值为8.002 304；两步法收敛代数为132代，收敛最优解为(0.519 99，0，3.480 51)，最优值为0.270 642 1．三步法分别求解了乐观最优解和悲观最优解，而两步法求解不了乐观最优解和悲观最优解的任意一种．

对于2+3维：乐观过程收敛代数为48，收敛最优解为(0，0，3.50e-03，0，3.996 97)，最优值为2.366e-04；悲观过程收敛代数为199，收敛最优解为(1.362 97，1.310 36，1.327 18，2.63e-08，0)，最优值为5.336 414；两步法收敛代数为195代，收敛最优解为(0.494 50，0.273 02，0，6.046 59e-02，3.172 52)，最优值为0.322 986 4．3种迭代运算应该还有继续收敛到更优解的可能，但最优解和最优值的精度已经很高，可以认为三步法分别求解了乐观最优解和悲观最优解，而两步法求解不了乐观最优解和悲观最优解的任意一种．

算例5：

算例5的反应集为：

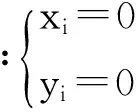
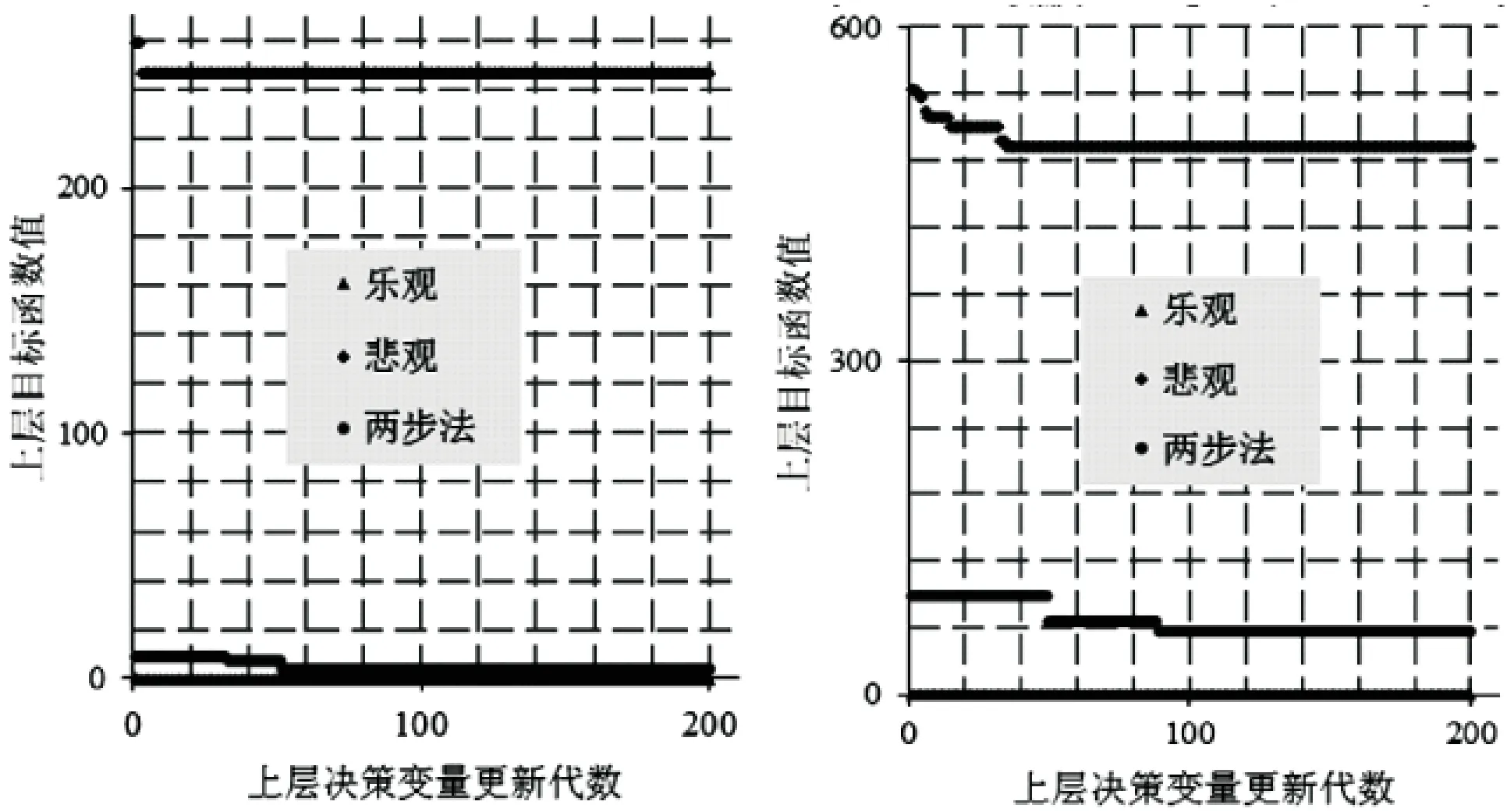
图9　算例5迭代过程(左边是2+2维，右边是4+4维)

对于2+2维：乐观过程收敛代数为189，收敛最优解为(1.05e-08，-3.20e-10，1.01e-08，-8.76e-10)，最优值为2.125e-016；悲观过程收敛代数为6，收敛最优解为(1，-1，-11.056 0，11.056 0)，最优值为246.471 4；两步法收敛代数为132代，收敛最优解为(0.421 2，1，0.435 6，1.570 8)，最优值为3.835 109．三步法分别求解了乐观最优解和悲观最优解，而两步法求解不了乐观最优解和悲观最优解的任意一种．

对于4+4维：乐观收敛代数为144代，收敛最优解(3.31e-10，3.57e-10，1.20e-08，4.80e-12，4.19e-09，-3.39e-08，2.89e-09，-4.73e-09)，最优值为1.342e-15；悲观过程收敛代数为35，收敛最优解为(1，-1，1，1-11.056 1，11.560 4，-11.056 1，-11.056 0)，最优值为492.945 5；两步法收敛代数为89代，收敛最优解为(0.799 921 9，0.497 671 3，-0.978 888 6，1.000 000，-4.068 758，-5.762 273，-1.364 951，1.570 795)，最优值为56.934 84．三步法分别求解了乐观最优解和悲观最优解，而两步法求解不了乐观最优解和悲观最优解的任意一种．

4结论

上述5个不同类型的算例的计算结果，不仅证明了三步法对于下层最优解不唯一的二层规划的适用性，也证明了对于下层最优解唯一的二层规划，三步法同样能有效地求解出其最优解，从而三步法对于二层规划具有普遍适用性．

由于三步法中多次进行了单层求解运算，运算时间相对较长．未来将致力于解决三步法的运算时间问题，并且将三步法运用于实际二层规划当中．

参考文献：

[1]运筹学教学编写组．运筹学[M]．北京：清华大学出版社，2005：143．

[2]Lucchetti R， Mignanego F， Pieri G. Existence Theorems of Equilibrium Points in Stackelberg[J]． Optimization, 1987, 18(6)：857-866．

[3]Dempe S. Foundations of Bilevel Programming[M]． Springer Science & Business Media, 2002．

[4]Bialas W F, Karwan M H. Two-level Linear Programming[J]． Management Science, 1984, 30(8)：1004-1020．

[5]Ben-Ayed O. Bilevel Linear Programming[J]． Computers & Operations Research, 1993, 20(5)：485-501．

[6]Dempe S, Schmidt H. On an Algorithm Solving Two-level Program Ming Problems with Nonunique Lower Level Solutions[J]． Computational Optimization and Applications, 1996, 6(3)：227-249．

[7]Dempe S. A bundle Algorithm Applied to Bilevel Programming Problems with Non-unique Lower Level Solutions[J]． Computational Optimization and Applications, 2000, 15(2)：145-166．

[8]Loridan P, Morgan J. ε-regularized Two-level Optimization Problems：Approximation and Existence Results[M]//Optimization. Springer Berlin Heidelberg, 1989：99-113．

[9]Loridan P, Morgan J. On Strict ε-solutions for a Two-level Optimization Problem[C]//Papers of the 19th Annual Meeting/Vortr?ge der 19. Jahrestagung. Springer Berlin Heidelberg, 1992：165-172．

[10] Sinha A, Malo P, Deb K. Test Problem Construction for Single-objective Bilevel Optimization[J]． Evolutionary Computation, 2014, 22(3)：439-477．

[11] Gao Y, Zhang G, Lu J, et al. Particle Swarm Optimization for Bi-level Pricing Problems in Supply Chains[J]． Journal of Global Optimization, 2011, 51(2)：245-254．

[12] Loridan P, Morgan J. Approximate Solutions for Two-level Optimization Problems[M]． Birkhäuser Basel, 1988．

[13] Aiyoshi E, Shimizu K. A Solution Method for the Static Constrained Stackelberg Problem Via Penalty Method[J]． Automatic Control, IEEE Transactions on, 1984, 29(12)：1111-1114．

[责任编辑王康平]

收稿日期：2015-11-05

基金项目：国家自然科学基金(51479142,51339004)，湖北省水利重点科研项目(HBSLKL201304)，湖北水利科研项目(HBSLKY201401)

通信作者：胡铁松(1964-)，男，教授，主要研究方向为运筹学．E-mail：tshu@whu.edu.cn

DOI：10.13393/j.cnki.issn.1672-948X.2016.02.023

中图分类号：O224

文献标识码：A

文章编号：1672-948X(2016)02-0102-06

Three-step Method for Solving Bilevel Programming with Non-unique Lower Level Optimal Solutions

Wang JianHu TiesongWang Qin

(State Key Laboratory of Water Resources & Hydropower Engineering Science, Wuhan Univ., Wuhan 430072, China)

AbstractBased on optimistic and pessimistic bilevel programming with non-unique lower level optimal solutions, the definitions of optimistic and pessimistic feasible solution is proposed, three-step method for solving bilevel programming with non-unique lower level optimal solutions is also proposed. Finally, the proposed three-step method and two-step method proposed before have been applied to 5 benchmark problems. The numerical results demonstrate the feasibility and effectiveness of three-step method.

Keywordsbilevel programming;optimistic optimal solution;pessimistic optimal solution