基于PFC2D的镁碳质耐火材料断裂行为模拟研究

常庆明，程　钊，袁丹丹，张　浩，桑绍柏，潘成刚

(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北 武汉，430081)



基于PFC2D的镁碳质耐火材料断裂行为模拟研究

常庆明，程钊，袁丹丹，张浩，桑绍柏，潘成刚

(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北 武汉，430081)

将镁碳质耐火材料视为骨料和细粉基质组成的两相复合材料，采用基于离散元的颗粒流模拟软件PFC2D，将材料离散成刚性颗粒组成的模型，把颗粒细观参数的变化与宏观力学特性联系起来，构建镁碳质耐火材料在1000 ℃下的试验模型，模拟试样三点弯曲的载荷-位移曲线，对材料裂纹的扩展进行分析，并通过改变摩擦系数、平行粘结刚度比、孔隙率以及平行粘结弹性模量，对比分析细观参数对载荷力峰值大小的影响情况。结果表明，采用PFC2D可准确模拟镁碳质耐火材料在三点弯曲时的断裂行为；材料的摩擦系数和平行粘结弹性模量与试样所受最大载荷力呈正比关系，而孔隙率和平行粘结刚度比与试样所受最大载荷力呈反比关系。

镁碳质耐火材料；离散元；三点弯曲；断裂行为；细观力学；颗粒流；PFC2D

镁碳质耐火材料因具有优良的抗渣侵蚀性和抗热震性，被广泛用于转炉、电炉、RH炉内衬以及钢包渣线等部位。随着高效率、低成本洁净钢冶炼新技术的发展以及节能降耗要求的提高，传统镁碳质耐火材料的低碳化成为必然的发展趋势。但低碳化后，镁碳质耐火材料的抗热震性会急剧劣化。镁碳质耐火材料热震损坏过程的实质是材料中裂纹扩展引起的失稳过程。由于实验的局限性，目前针对耐火材料断裂行为的研究主要以数值模拟为主，然而通常的数值模拟，例如有限元法，对于耐火材料破裂过程中多裂纹体系的扩展计算效果并不好，难以全面阐释耐火材料的损毁机理。

离散元法作为一种新的数值计算方法，它可以用来描述材料的大变形问题，通过在散粒体颗粒之间施加上链接，便可用来模拟在外荷载作用下连续介质向非连续介质转化的力学问题[1]。基于离散元的颗粒流模拟软件PFC把整个介质看作由一系列离散化、独立运动的颗粒组成，通过圆形颗粒的运动及其相互作用来研究物质的力学性能。PFC被广泛应用于颗粒材料损伤断裂机理的研究中，如常明丰等[2]对不同颗粒粒径范围的颗粒材料双轴试验进行PFC模拟，分析了围压变化对不同材料的弹性模量和强度的影响,以及在不同加载速率下材料的弹性模量、泊松比和强度的变化规律，但尚未见PFC在耐火材料断裂行为相关研究中的应用。由于耐火材料颗粒之间存在胶结材料，通常的数值模拟无法直观模拟其作用，而采用PFC模拟，模拟程序中的平行粘接模型可以在相互接触的颗粒间传递力和力矩[3-5]，更加符合耐火材料的特性，因此具有很强的优越性。为此，本文拟利用PFC2D软件，采用反向模拟法确定镁碳质耐火材料的细观参数，对其在1000 ℃下三点弯曲时裂纹的产生、扩张及贯通行为进行模拟，并分析各细观参数对材料载荷力峰值的影响。

1　试样的制备

以70%(质量分数，下同)的电熔镁砂骨料和含22%的氧化镁粉末、5%的鳞片石墨及少量金属铝粉和单质硅粉的预混合细粉为原料，以热固性酚醛树脂为结合剂，在小型混砂机中依次加入电熔镁砂骨料、液态酚醛树脂以及预混合细粉混匀，在150 MPa的成型压力下成型为140 mm×25 mm×25 mm的条状试样后在200 ℃下保温24 h进行固化处理，最后在埋炭气氛下于1000 ℃下热处理3 h后取出试样。经过以上处理后的试样，在室温下进行三点弯曲实验，即可观察到近似于耐火材料在1000 ℃下三点弯曲时的开裂行为。

2　PFC2D模型的建立

在PFC2D中建立实样三点弯曲实验的二维模型，建模尺寸及建立的二维模型如图1所示。建模时，首先采用Clump(丛簇)模型，根据电熔镁砂的密度(3000 kg/m3)和颗粒半径(1.1～1.3 mm)，用圆形颗粒来随机生成骨料，再用细小的圆形颗粒生成细粉基质(密度为2000 kg/m3，颗粒半径为0.25～0.5 mm)[4,6]。由于系统在自动生成颗粒单元的过程中，容易出现局部部分颗粒无法与周围颗粒形成有效接触而形成悬浮，这些悬浮的颗粒会使粘结模型生成较大的孔隙，并且对模型的受力状态有很大的影响，造成计算结果失真，因此，在给模型细观力学参数赋值之前，悬浮的颗粒必须消除[3]。

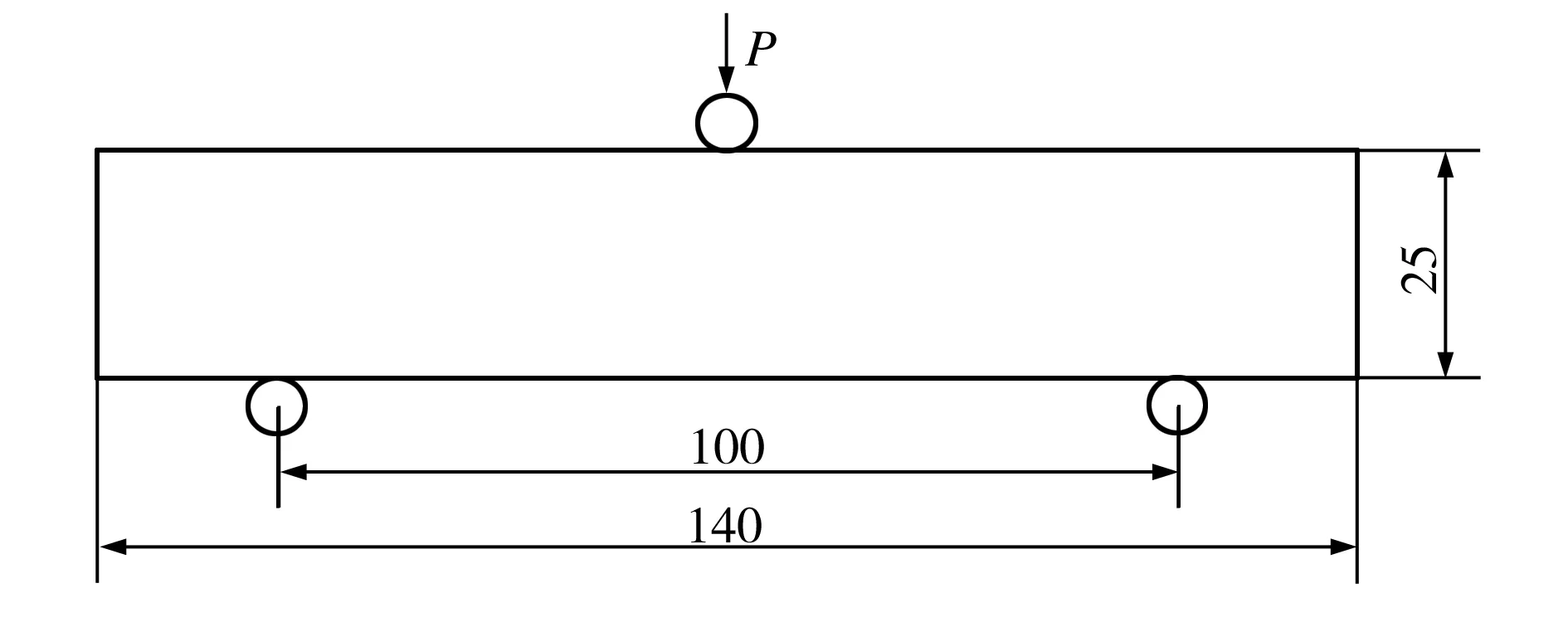
(a)模型的几何尺寸

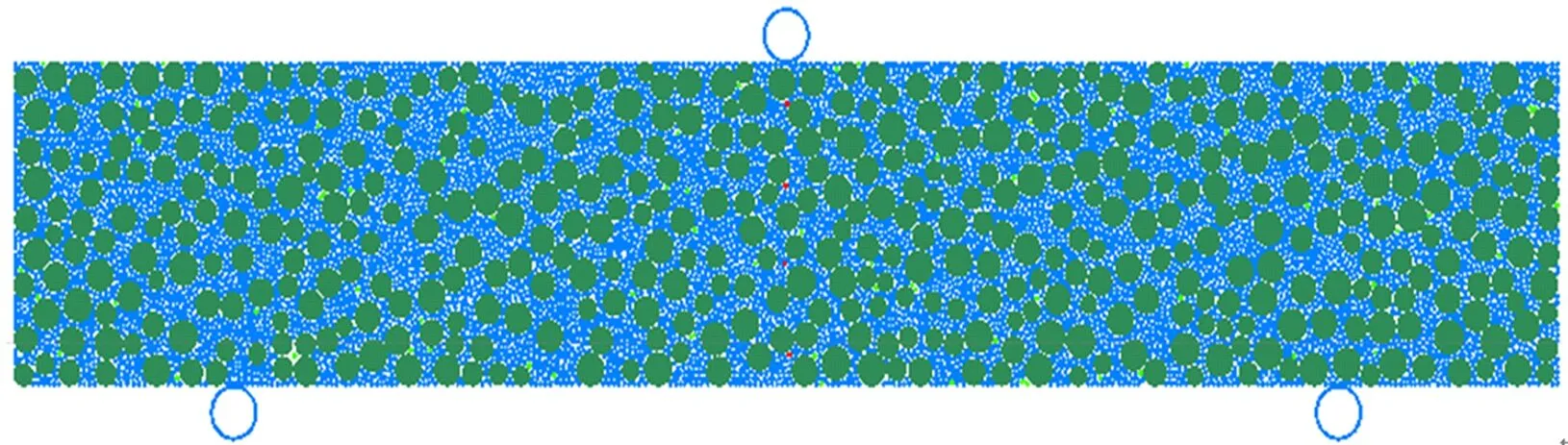
(b)PFC2D模型

3　细观力学参数的确定

耐火材料宏观力学性能不仅受到原料颗粒大小、形状和分布的影响，还与颗粒、基质胶结物的变形和强度特性有关。通过实验可以很方便地调试连续体模型介质中的宏观力学参数。但对于PFC2D而言，其模型不同于连续体介质模型，模拟仿真时模型细观参数值主要采用反向模拟的方法来确定，即将模拟结果与实验结果进行对比，不断地调整组成模型材料的各个基本颗粒单元的级配和链接方式，直至模拟结果与试验结果的误差达到要求[7]。

本文采用反向模拟的方法确定了镁碳质耐火材料在1000 ℃时骨料和基质的细观参数如表1所示，其中平行粘结刚度比等于平行粘结法向刚度与平行粘结切向刚度之比。此参数下模拟得到的三点弯曲试样载荷力-位移曲线与实验结果的比较如图2所示。由图2中可以看出，实验及模拟结果的峰值分别为695.98 N 和727.32 N，两者的误差仅为4.5%，也就是说，此时数值模拟结果与实验结果基本相符。

表1　骨料和基质的细观参数

图2　载荷力-位移曲线

4　裂纹扩展过程分析

图3所示为试样三点弯曲破坏过程中裂纹的产生、扩张过程的模拟结果。从图3(a)可以看出，裂隙大致在试样的中间位置开始产生，最终破裂位置与实验破坏情况相符。由图3(b)中可见，实验开始阶段，试样受力产生弯曲变形，当载荷力达到某一值时，试样会在局部出现细小裂纹，此时并没有表现裂纹的宏观性；随着载荷力的持续增加，细小裂缝扩张，且沿着骨料边界曲折扩展，骨料与基质的界面粘结失效，在界面处的裂纹越来越明显，最终互相延伸、连接以及贯通，形成宏观裂纹。

图4、图5分别为试样三点弯曲实验中载荷力达到最大值时内部颗粒的速度矢量图及运动时内部颗粒受不平衡力的矢量图。从图4中可见，试样只有断裂面颗粒与基质有较明显的相对运动，而断裂面以外的其余颗粒速度基本为零；试样在受到载荷力时，试样中部的颗粒速度方向是分别向两边运动的，表明产生裂纹处受到的是拉应力，这就解释了裂纹从中间产生的原因。从图5中可以看出，试样与载荷物的接触处以及试样中部受力最大。

(a)最终裂纹

(b)裂纹扩展过程

图4　速度矢量图

图5　不平衡力矢量图

5　细观参数对试样最大载荷力的影响

如前所述，PFC2D模拟分析中细观参数的确定需通过反向模拟法与实验值进行反复比较得到，其过程较为复杂。为了减少反向模拟中的计算量，在此探讨细观参数对材料宏观力学性能的影响规律，以期为PFC2D模拟中细观参数的快速选择提供借鉴。由于耐火材料可以看作是由骨料和基质组成的二相复合材料，因此基质与骨料之间的细观参数对材料的宏观力学性能有较大的影响。由于单独改变某一个细观参数进行模拟时，得到的载荷力-位移曲线趋势大致相同，只是峰值大小不同，故本文仅探讨各细观参数的改变对试样最大载荷力的影响。

试样在三点弯曲实验的模拟中，材料断裂时的最大载荷力与各细观参数之间的关系如图6所示，其中图6(b)为基质和骨料的平行粘结法向刚度分别为4×109N/m和4×1010N/m时的结果。从图6中可以看出，随着颗粒间摩擦系数的增大，试样的最大载荷力逐渐增大，这是因为颗粒间的摩擦系数越大，颗粒滑移时所需的力越大，所建立起来的骨架结构强度越高，材料的承载能力就越高；当平行粘结法向刚度不变时，随着平行粘结刚度比的增大，试样的最大载荷力逐渐减小，这是因为当平行粘结法向刚度值为一定值，随着平行粘结的法向刚度与切向刚度比值的增加，相当于按比例减小了平行粘结切向刚度值，导致其能承受的最大载荷随之减小；随着孔隙率的增大，试样的最大载荷力逐渐减小，这是由于孔隙率增大，材料内部的空隙增多，相应地微裂缝越多，越容易出现裂纹，因此其承载能力降低；颗粒间的平行粘结弹性模量越大，试样的最大载荷力越大，且近似呈线性变化，这是由于耐火材料的宏观变形是由颗粒实体本身的变形和颗粒与颗粒之间的位置改变造成的，随着平行粘结弹性模量的增大，颗粒集合体抵抗外部载荷的能力也增加，抗压强度增大，所能抵抗的最大载荷力也增大。

(a)摩擦系数

(b)平行粘结刚度比

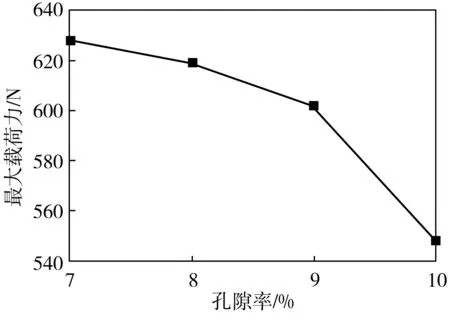
(c)孔隙率

(d)平行粘结弹性模量

综上所述，根据以上4个细观参数对试样三点弯曲时最大载荷力的影响趋势，可以较方便地通过改变这4个参数来调节模拟时的最大载荷力。

6　结论

(1)采用基于离散元法的颗粒流模拟PFC2D模拟耐火材料在1000 ℃时三点弯曲实验，可以观察到在加载过程中颗粒运动的速度矢量及不平衡力矢量分布，清晰再现材料破坏过程，其得到的材料破坏位置及裂纹扩展形式与实验结果相一致，验证了该模拟方法的可行性。

(2)采用PFC2D对镁碳质耐火材料三点弯曲实验中裂纹的扩展进行离散元模拟分析时，骨料与基质的细观参数中摩擦系数和平行粘结弹性模量与试样所受载荷力的峰值呈正比关系，而孔隙率和平行粘结刚度比与试样所受载荷力的峰值呈反比关系，因此可以依据以上规律，通过合理改变这4个细观参数来快速调节最大载荷力的大小。

[1]刘凯欣，高凌天．离散元法研究的评述[J]．力学进展，2003，33(4)：483-490．

[2]常明丰，裴建中，陈拴发．颗粒材料双轴试验离散元数值模拟[J].交通运输工程学报,2010,10(5):1-7.

[3]宿辉，唐阳，聂汉江．基于PFC2D不同细观参数对生态混凝土宏观破坏分析[J]．科学技术与工程，2014，14(28)：118-124．

[4]许尚杰，尹小涛，马双科，等．基于颗粒流的混凝土材料数值实验研究[J]．实验力学，2009，24(3)：251-258．

[5]Cho N，Martin C D，Sego D C．A clumped particle model for rock[J]．International Journal of Rock Mechanics and Mining Sciences，2007，44：997-1010．

[6]周健，池永，池毓蔚，等．颗粒流方法及PFC2D程序[J]．岩土力学，2000，21(3)：271-274．

[7]周博，汪华斌，赵文锋，等．黏性材料细观与宏观力学参数相关性研究[J]．岩土力学，2012，33(10)：3171-3178．

[责任编辑郑淑芳]

PFC2D-based simulation study of the cracking behavior of MgO-C refractory

ChangQingming，ChengZhao，YuanDandan，ZhangHao，SangShaobai，PanChenggang

(Key Laboratory for Ferrous Metallurgy and Resources Utilization of Ministry of Education, Wuhan University of Science and Technology, Wuhan 430081, China)

MgO-C refractory material is regarded as a two-phase composite material consisting of aggregate and fine powder. In this study, particle flow simulation software PFC2D,which is based on discrete elements,was employed to discretize the material into a rigid particle model, and the microscopic variation of the particles was related to the macroscopic mechanical properties of the material. Under 1000 ℃, the experimental model of the MgO-C material was established, and three-point bending load-displacement curves of the samples were simulated. Material crack propagation was analyzed, and by changing the friction coefficient, parallel bond stiffness ratio, porosity and elastic modulus of the whole model, the influence of microscopic parameters on the value of the peak load was compared. The results show that PFC2Dcan accurately simulate the three-point bending fracture behavior of the magnesium carbon refractory material. The friction coefficient and parallel bond elasticity modulus of the material are proportional to the peak load force of the samples, and the porosity and the parallel bond stiffness ratio of the material are inversely proportional to the peak load force of the samples.

magnesia-carbon refractory；discrete element；three-point bending；fracture behavior；micro mechanics；particle flow；PFC2D

2016-01-27

国家自然科学基金资助项目(51372176).

常庆明(1964-)，男，武汉科技大学教授，博士.E-mail:qmchang@163.com

TQ175.1+5

A

1674-3644(2016)04-0273-05