基于最小二乘法离场航迹构造方法
2016-08-01张晓娜耿笑寒
张晓娜 叶 子 薛 成 耿笑寒 谢 颖
基于最小二乘法离场航迹构造方法
张晓娜1叶子2薛成2耿笑寒2谢颖2
1.中国民航大学理学院;2.中国民航大学计算机科学与技术学院张晓娜,女,本科,中民民航大学,研究方向为计算机图形学。
国家级基金项目:中国民航大学大学生创新创业训练计划项目(201510059012)

行业曲线
创新点 :本文提出了一种基于最小二乘法离场航迹逆向构造方法。此方法与目前的构造方法相比较创新点有三点:第一点,采用最小二乘法结合两种离场方式特征逆向推出离场航迹最佳匹配函数,使得离场水平面航迹更加准确、平滑;第二点,解决了在离场数据、飞行计划及气象资料缺失的情况下,无法对飞机离场航迹进行构造的问题;第三点,构造了基于贝叶斯推理的飞机离场航迹选择评分函数,从而保证了离场方式的准确性。
本文提出了一种基于最小二乘法离场航迹逆向构造方法。该方法解决在离场数据、飞行计划及气象资料缺失的情况下,无法对飞机离场航迹进行构造的问题。通过构造基于贝叶斯推理的飞机离场航迹选择评分函数,验证离场方式的选取方法的有效性。实验表明该方法不仅解决了在飞机离场信息缺失的情况下离场航迹的构造问题,而且确保了飞机起飞方式的准确性。
飞机离场航迹是飞机起飞过程的形象化体现。目前,飞行航迹的构造方法通常采用两类方式,第一类是在飞行计划确定及气象资料完整的情况下,结合飞行动力学和运动学模型正向推导的方法。飞机起飞航迹计算方法研究 提出了对不同机型统一的离场航迹构造方法,该方法主要针对离场航迹剖面进行了构造,缺少对水平投影面构造的方法;基于ANP数据库的飞机起飞仿真研究是基于详细的飞行资料和性能参数的前提下,提出了飞机离场剖面航迹构造方法;离场航迹降噪优化设计的多目标智能方法是一种利用航段飞行特征约束求解离场航迹的方法。第二类是在拥有较为准确的雷达位置信息点的情况下对雷达数据去噪,拟合出最佳函数匹配从而得到平滑的航迹。经纬仪目标交汇测量及航迹曲线拟合文中提出根据不同时刻的坐标,用最小二乘法对目标航迹进行拟合,从而推测下一时刻的位置速度及加速度;三维航迹的B样条曲线拟合算法利用B样条曲线的几何性质,解决了飞行器三维航迹拟合中的边界条件等约束问题。第二类多用于飞机离场结束后航迹的拟合。上述提出的两类方法用于离场航迹的构造存在以下三种问题:一是由于飞机离场属于低空飞行,雷达捕捉飞行器在低空飞行的位置信息不准确,飞机离场的雷达点相比于真实点误差较大,且飞机离场的方式不同,导致无法单一的利用拟合离场雷达数据的方法确定离场航迹。二是现有方法多为对离场剖面航迹进行构造,忽略由于离场方式的不同导致水平面航迹存在误差。三是在离场数据、飞行计划及气象资料缺失的情况下,无法对飞机离场航迹进行构造的问题。由此本文为了解决上述问题,采用最小二乘法结合两种离场方式特征,提出离场航迹逆向构造方法。
相关工作
飞机离场过程是指飞机高于起飞表面450m(1500ft),并完成从起飞到航路形态的转变,达到规定的速度和爬升梯度。飞机起飞过程包括起飞场道滑跑阶段和起飞航道阶段。起飞航迹依据飞机的构型、发动机的推力状态、对爬升梯度的要求等分为第一爬升阶段、第二爬升阶段、第三平飞阶段、最后爬升阶段等四个阶段。本文忽略平飞过程,把此过程与第四阶段融合在一起下文统称第三阶段,分别对第一、二及三阶段分别进行构造。
最小二乘法是通过最小化误差的平方和求得待定系数从而寻找数据的最佳函数匹配。假设多项式:
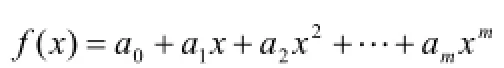
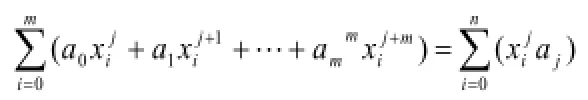
得方程组:
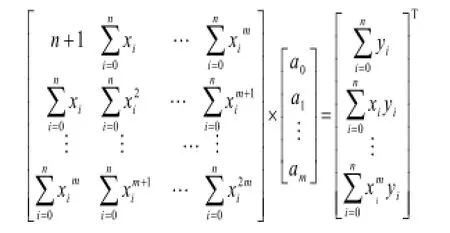
该方程组称为多项式拟合的法方程,令:
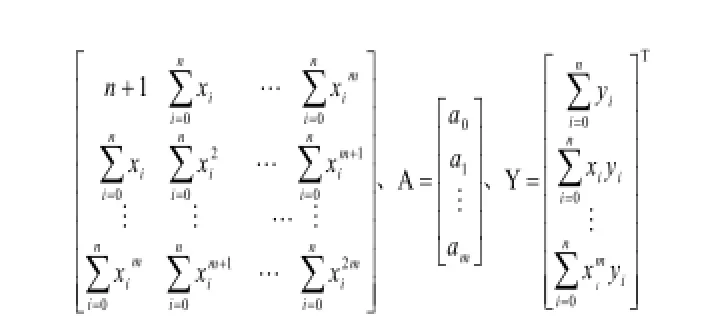
贝叶斯推理需要根据当前所观察到的样本信息及现有经验和知识得出结论,以估计和假设检验为基础发展出的一种归纳推理方。具体方法为已知一个事件集其中每一Bi的概率为p(Bi),又知在Bi已发生的条件下A事件发生的条件概率p(A/Bi),就可通过以下公式得出在给定A已发生的条件下任何Bi发生的条件概率p(Bi/A)即:
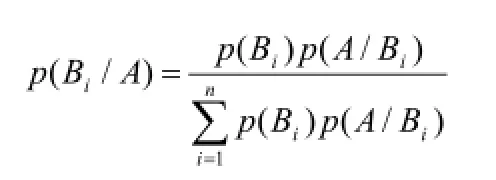
基于最小二乘法飞机离场航迹逆向构造方法
飞行高度在350m以上的雷达监测位置信息点较为准确,本文把航迹投影到水平面和剖面分别构造,并利用准确数据逆推离场航迹。首先根据两种离场方式特征判别离场方式,其次利用350m以上的雷达监测位置信息点分别拟合两种离场方式的第三阶段航迹水平面投影,最后计算各阶段关键参数确定滑跑航迹及运动过程。不得不提在离场数据、飞行计划、气象资料缺失前提下。起飞过程模拟难度很大,为了确保模拟的航迹准确性,不可避免需要根据飞机的离场规则,假设合理数值。点为已知飞机在跑道滑跑的加速始点,此点的各方向速度均为V0=0,点为飞机的离地点,其中z1已知为地平面高度,为直线离场时高度为z21=122+z0时的坐标点 ,转弯离场时为转弯点,为已知雷达数据第一个点。
基于贝叶斯推理的飞机离场方式估计方法
直线离场方式特征:特征一,起始离场航线与跑道中线方向角度相差小于15°;特征二,离场航迹偏于跑道中线一侧而在DER(离场末端)的横向距离不大于300m。但只要实际可能,离场航线就应与跑道中线延长线一致。转弯离场方式特征:离场过程中出现离场角度要求大于15°的转弯,并且规定在飞机起飞离场到达DER标高之上才允许转弯,在此之前为直线飞行。
由于已知雷达数据的高度值不同分为以下两种情况,利用不同的离场特征分别作为判别离场方式的依据。
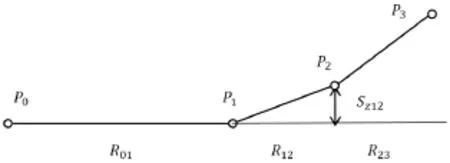
图1 飞机离场示意图
(1) 现有雷达数据高度值在450m以上,飞机可能已经结束离场并立即发生转弯,由雷达数据得到的航线与跑道中线的夹角大于15°不能说明转弯发生在离场过程中,因此不能用特征一判断,利用特征二更加适合。利用特征二区分时,计算雷达数据第一个点与跑道直线的水平距离如果小于300m则为直线,否则为转弯。
(2)现有雷达数据高度值在450m以下,飞机还未结束离场,利用特征一就可以判断。已知离场结束后航迹的雷达数据,前几个点组成的航迹是顺沿离场航迹的方向产生,继承了离场方向变化趋势。利用特征一区分时,利用前四个数据点进行一次的最小二乘法拟合方程,跑道直线方程,由正切公式计算两直线夹角,则,当时为转弯离场,否则为直线离场。
为了检验上述判断方法的准确性构建飞机离场方式选择评分函数。因为飞机离场方式主要分为两种,一为直线(line)式离场,一为转弯(arc)式离场,两类飞机离场模型互相独立互为补集。所以根据以上特征,简单化问题,可以化为非此及比的模型。由此就可以根据概率论的乘法定理及贝叶斯公式求得P(line/w)及P(arc/w)。P(line/w)物理意义为在一定特征事件的基础上飞机是直线离场,P(arc/w)物理意义为在一定特征事件的基础上飞机是转弯离场。公式:
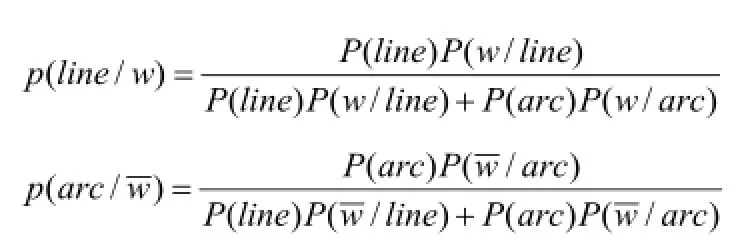
综上,评分规则为:满分为100分。若直线起飞方式分数为P(line/w)×100,转弯起飞方式起飞分数为,
通过分数检验离场方式区分方法的准确性。
爬升阶段构造方法
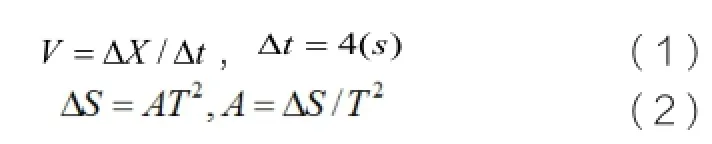

其中V0=0得。
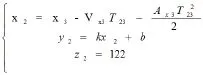
转弯离场方式:利用现有雷达数据点作二次的最小二乘法拟合,拟合出的曲线方程为F2(x)。跑道中线坐标已知,任取跑道中线两点坐标计算跑道直线方程F1(x)。拟合出的二次曲线方程与跑道中线求交点,此交点为转弯点P2。
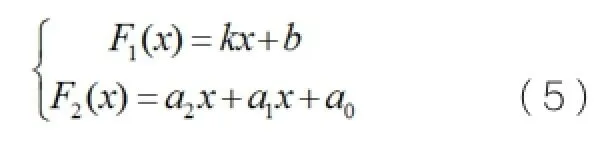
解得:
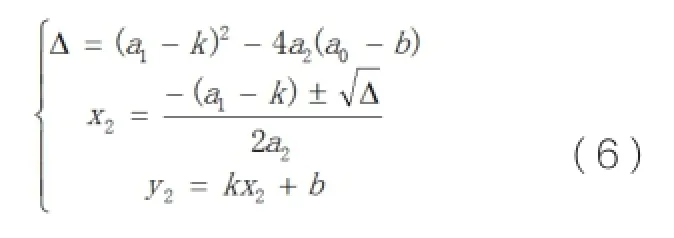
机起飞的方向比对两种计算结果的大小,决定∆的正负情况,当起飞方向X轴上的数值是增加的则取两种计算结果较大值,反之取较小。
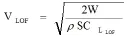
计算X、Y轴方向的离地速度

并对其进行单位转换。其中θ=arctan(k),k为跑道直线方程斜率。转弯离场P2点X轴坐标已知,但高度未知。转弯离场的计算方法与直线不同,转弯离场,由公式(3),(4),(5)计算:
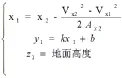
计算转弯离场点的Z轴方向坐标。转弯高度计算公式:
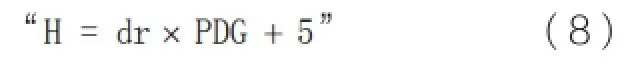
补充两个阶段之间每隔四秒的坐标。直线离场方式:利用X、Z轴加速度及F1(x)直线方程及坐标P1(x1,y1,z1)及P2(x2,y2,z2)计算。转弯离场方式:利用X、Z轴加速度及F2(x)计算。下方公式中j表示第j阶段,n表示为j阶段第n个坐标值,t等时间间隔4s,T为j阶段的总时间,
公式为:
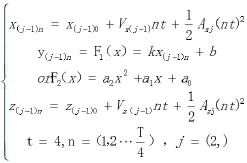
起飞场道阶段构造方法
飞机在地面加速滑跑时,其受到的外力包括发动机推力T、升力L、阻力D、地面的支撑力N、摩擦力F、起飞地面滑跑阶段通常认为飞机的迎角、发动机的安装角均为小量。实际上近似计算飞机滑跑距离时,可将地面滑跑阶段发动机的推力取平均值并视为常数,同样计算摩擦系数也取其平均值并看作常数,于是可得飞机地面起飞滑跑阶段速度为V0=0加速到离地速度VLOF的滑跑距离为:
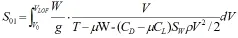
便于估算引入“换算摩擦系数”µ',其值为:
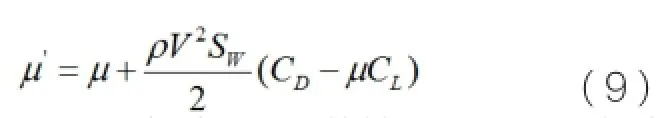
在实际计算起飞滑跑距离时,可以将地面滑跑期间发动机的推力取平均值并视为常数,同样换算摩擦系数也取其平均值并看作常数,飞机地面滑跑距离的近似估算公式:
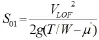
距离差已知公式为:
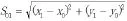
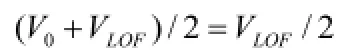
作为地面滑跑时的平均速度,则有
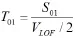
合加速度单位为m2/s
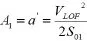
得X、Y轴加速度为:
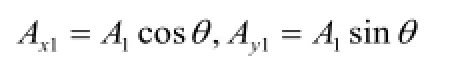
利用X、Z轴加速度、速度、F1(x)直线方程及坐标P0(x0,y0,z0)补充三个阶段之间每隔四秒的坐标。公式为:
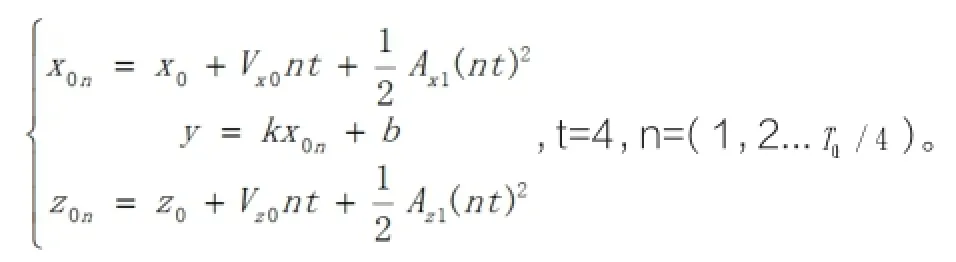
综上飞机离场航迹由此确定。
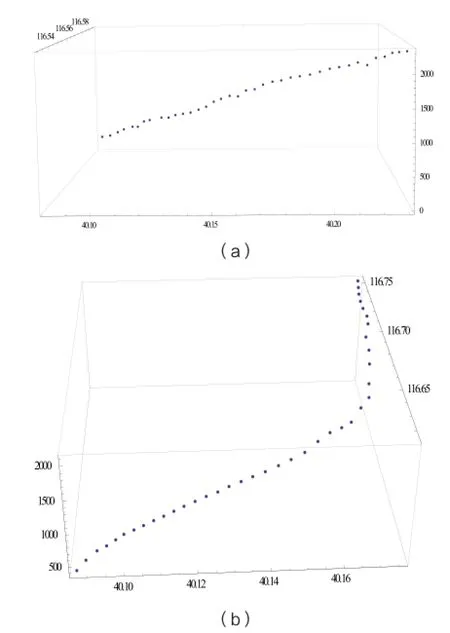
图2 原始数据三维散点图

图3 航迹构造前后对比结果
方法验证
本实验以首都机场为例,采用首都机场提供的2013 年4、5月的飞机飞行数据及机场地理位置信息,随机抽取1000条离场航迹进行实验。首先,依据构造方法对数据进行处理拟合出离场航迹,利用拟合出的航迹计算出飞机离场滑跑距离及转弯高度,查看计算出的上述参数是否符合飞机离场规定,从而验证方法的有效性。利用基于贝叶斯推理的飞机离场方式选择评分函数计算分数,验证飞机离场方式选择方法的准确性。
为了大致了解离场航迹线的特点,利用雷达数据做出三维散点图。进而根据航迹线水平面的投影的特征对航迹线进行分类。航迹线水平面投影类型分为两类,第一类为近似顺延跑道延长线如图2(a)。第二类为偏离跑道延长线,在跑道的一侧与跑道延长线形成较大夹角如图2(b)。从对雷达数据初步分析可以看出本文对离场模型的分类假设是正确的。
图3(a)和(b)分别为直线离场实验前350m以上原始雷达数据三维曲线图和实验后效果图。图2(c)和(d)分别为转弯离场实验前350m以上原始雷达数据三维曲线图和实验后效果图。通过实验效果前后对比可以看出利用本文方法构造出的离场航迹与实际情况较为一致。
由表1可以看出转弯高度均允许转弯高度值120m以上。滑跑距离在均合理范围以内。
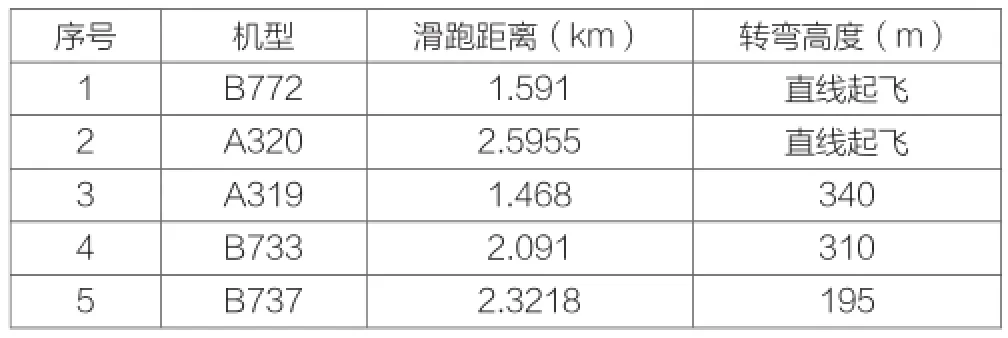
表1 飞机离场参数计算结果
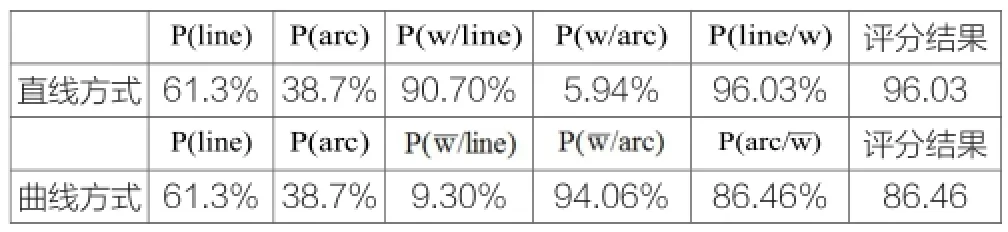
表2 离场方式的评分结果
由统计学办法得出P(line)及P(arc)。利用飞机离场方式选择方法从直线离场航迹中筛选出符合直线起飞特征的航迹及符合转弯起飞特征的航迹,从转弯离场航迹中筛选符合直线起飞特征的航迹及符合转弯起飞特征的航迹,利用统计学办法得出。最后利用评分方法计算评分。评分结果均在85分以上表明离场方式选择方法的准确度较高。
由图1和表2可以看出本文对离场模型的分类假设是正确的,离场方式选择方法准确度较高。由图2和表1可以看出本文构造出的离场航迹与实际情况一致。由此验证了基于最小二乘法离场航迹构造方法的有效性及准确性。
结语
本文提出了一种基于最小二乘法离场航迹逆向构造方法。新方法的可行性已在多次实验中得到验证。并利用基于贝叶斯推理的飞机离场航迹选择评分函数计算评分,评分结果理想,验证了离场方式的选取方法的有效性。新方法不仅可以利用于解决在飞行计划和气象资料缺失的前提下,无法对飞机离场航迹进行构造的问题,还可以为场间雷达与空中雷达连接方案的制定提供有利参考。
DOI:10.3969/j.issn.1001- 8972.2016.13.019
