非均匀组织医学超声非线性传播仿真
2016-08-01郑音飞
周 浩,郑音飞
(浙江大学 生物医学工程教育部重点实验室,浙江 杭州 310027)
非均匀组织医学超声非线性传播仿真
周浩,郑音飞
(浙江大学 生物医学工程教育部重点实验室,浙江 杭州 310027)
摘要:为了实现仿真医学超声波在非均匀组织中的传播过程,建立超声非线性传播计算模型.由软组织中一阶非线性波动方程推导得出“声压-质点振动速度”耦合超声非线性波动方程以降低求解复杂度.采用k空间方法对非线性波动方程组求解,在保证数值计算精度的同时降低计算的内存占用量和计算时间.通过与一维问题的解析解和二维问题的时域有限差分(FDTD)求解结果对比,验证所述模型的精度.在空间采样率为声波波长的1/9、Courant-Friedrichs-Lewy(CFL)数为0.3的情况下,所述模型的平方误差为0.012 5%,而时域有限差分方法(FDTD)的平方误差为42.5%.利用体腹壁组织数字模型,进行医学超声谐波成像仿真,验证谐波成像较基波成像能够提高深部组织区域的图像质量.
关键词:非线性声学;波动方程;超声成像;k空间方法;谐波成像
临床医学中应用的医学超声通常处于较高频带范围(1~10 MHz),这导致超声波在生物组织的传播过程中伴随有显著的非线性现象.医学超声的非线性效应已被应用于医学超声成像、高强度聚焦超声治疗和低强度超声理疗等方面[1-4].生物组织中超声非线性传播仿真可应用于医学超声换能器设计、新型成像算法开发、声束畸变校正研究和医师培训等领域[5-9].相较于传统线性声场的积分求解方法[10],生物医学超声非线性传播仿真的关键在于求解超声传播的非线性微分方程.利用算子分裂求解非线性Khokhlov-Zabolotskaya-Kuznetsov(KZK)方程是超声非线性传播仿真的常用方法[11-13],但KZK方程为抛物线型方程,仅能在较小的发射孔径内保证仿真精度,难以获得后向散射回波[14].利用时域有限差分方法求解非线性全波方程(full-wave equation),在仿真超声前向传播的同时可以获得后向散射回波,但由于超声波速与频率的限制,需要极高的时间-空间采样率以保证仿真精度[14-16].与时域有限差分(finite-difference time-domain, FDTD)方法不同,k空间方法采用傅里叶变换计算波动方程中的空间导数项,利用修正的差分算子计算时间导数项,从而可在较低的计算开销下保证仿真精度[17-18];然而,传统的k空间方法难以获得超声非线性传播时介质内质点振动速度分布情况,也难以直接应用完全匹配层(perfect matched layer, PML)方法抑制声波在仿真计算区域边界处的周期性入射.
本文在推导出一阶耦合超声非线性波动方程组的基础上,采用k空间方法模拟超声在组织中的非线性传播,同步获得生物组织中声压与质点速度的分布特性.此外,采用声压-速度耦合的波动方程组,可以直接将PML应用于k空间方法.通过超声非线性传播的解析解和FDTD解验证所提出方法的准确性.最后将该方法用于医学超声谐波成像仿真.
1理论
生物软组织中一阶非线性波动方程[19]为
(1)
式中:ρ′为超声传播导致的介质密度变化量,u为质点速度,p为声压,B/A为非线性参量,c0和ρ0分别为介质的平衡声速和密度,μ与μB分别为切变和膨胀黏滞系数,κ为热传导系数,cv与cp分别为定容和定压比热,t为时间.式(1)的数值求解较为复杂,为降低计算复杂度,式(1)可进一步合并:
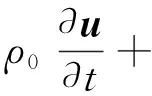
(2)

(3)
式中:β=1+Β/(2Α)为介质非线性参数,
δ1=κ(1/cv-1/cp)/ρ0,δ2=(μB+4μ/3)/ρ0,
两者分别为由热传导和组织黏滞导致的超声衰减参数;δ1+δ2=δ,δ为声衰减参数,由于在生物组织中热传递导致的声衰减占总衰减比例甚少[19],在本研究中经验性地认为δ2=0.01δ.为了对式(3)以k空间方法求解,需要对等号右边的非线性项进行改写.式(3)中的非线项为二阶小量,而声压与质点振动速度线性关系在一阶精度下成立:

(4)
可将式(4)代入式(3)中的非线性项而不影响等式推导的精度[13],则式(3)可写为

(5)
利用时间交错网格,设Δt为时间步进长度,采用时域显格式在时域采样点nΔt (n=1, 2, …)上对声压p进行离散、在时域采样点(n+1/2)Δt上对质点运动速度u进行离散,则离散后的一阶非线性波动方程组(2)与(5)可写为

ξ=x, y,z.
(6)
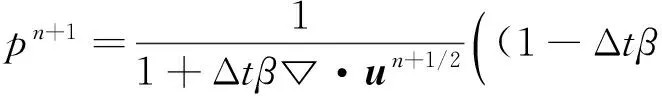
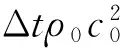
(7)
式中:n为时间节点,ξ为质点速度矢量方向标志.为了抑制时间导数离散引起的数值色散,利用k空间方法计算式(6)与(7)中的空间导数:
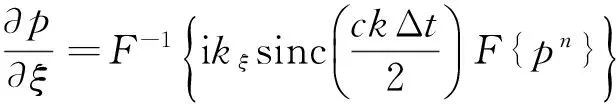
(8)

(9)

由于离散傅里叶变换具有周期性,从计算边界一侧入射的声波会从对侧边界出射,本研究中直接利用一阶完全匹配层方法使声波在计算边界处发生衰减[18,20].
2仿真实验
2.1均匀介质中的非线性传播仿真
为了验证所述方法对声波非线性传播模拟的精度,对单频平面波在衰减介质中的传播进行仿真.在单频连续平面声波非线性传播的情形下,式(1)转化为Burgers方程,其解析解由文献[21]给出.在本研究中,设定源点声压为
p=p0sin(2πf0t).

图1 单频平面波在衰减介质中非线性传播仿真结果Fig.1 Plane wave nonlinear propagation simulation in homogeneous lossy medium

2.2非均匀介质中的非线性传播仿真
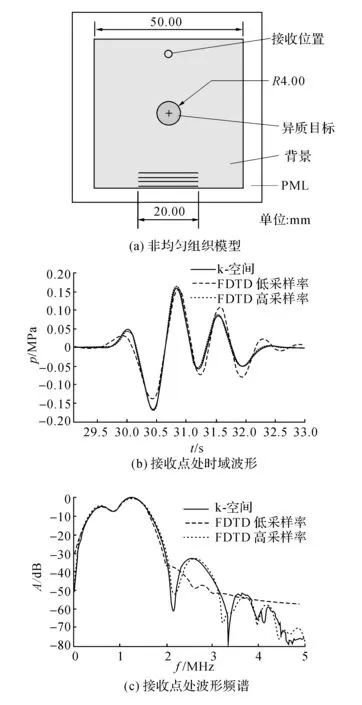
图2 非均匀介质超声传播仿真Fig.2 Acoustic wave nonlinear propagation simulation in a heterogeneous medium
由于人体组织声学参数的非均匀性,医学超声波在人体组织中传播时将发生折射、散射等现象.为了验证所述方法对非均匀介质声波非线性传播的准确性,令声波在如图2(a)所示的二维非均匀介质中传播.此非均匀介质由圆形异质物和均匀背景组成,均匀背景为50mm×50mm矩形,圆形异质物半径为4mm,位于均匀背景中央,距圆形异质物中央20mm处设置声波接收点.为了与人体各类型组织间声学参数相似,均匀背景介质声速设为1 500m/s,密度为1 000kg/m3,非线性参数为3.5,并设其为无衰减介质;圆形异质物的声速设为1 575m/s,密度为1 050kg/m3,非线性参数为4.0,超声衰减参数为1×10-4m2/s.令超声发射孔径位于均匀背景介质的底端,以平面波方式向介质内发射声波.声波发射孔径为20mm,发射波形为加Hanning窗的2周期正弦波,正弦波频率为1MHz,发射波形最高幅度为0.25MPa.在使用k空间方法时,设定空间采样间隔为非均匀介质中声波最小波长的1/9,CFL=0.3.采用同样的仿真参数,利用FDTD方法进行仿真以对比结果,分析在较低空间分辨率下两种方法的精度.同时,以空间采样间隔为非均匀介质中声波最小波长的1/27,CFL=0.1为仿真参数,进行高时间-空间分辨率下FDTD仿真以对非均匀介质中声波传播仿真提供基准.图2(b)为3种仿真方法下,声波接收点接收到的声压波形,可见k空间方法所得结果与基准结果高度符合,体现出k空间方法在低空间分辨率情况下的优势.图2(c)为声波接收点接收波形的频谱A(f).k空间方法所得波形频谱与基准波形在基频与一次谐波附近吻合较好;由于k空间方法采用的空间采样率较低(9倍基频波波长),对4MHz以上的频率成分不能有效采样.由图2(c)还可见,在低空间分辨率下FDTD方法几乎不能有效包含声波的非线性频率成分.
2.3超声谐波成像仿真
在验证了所述方法对超声波在非均匀介质中传播仿真准确性的基础上,对医学超声线阵探头所发聚焦声波在非均匀人体组织中的传播进行模拟,并采集后向散射回波,进行超声谐波成像仿真.

图3 超声谐波成像仿真Fig. 3 Simulation of tissue harmonic ultrasound imaging
仿真中设定空间采样间隔为33.87μm,CFL=0.3,模拟的换能器型号为UltrasonixL9-4/34高频线阵换能器,阵元数N=128,阵元中心间距为0.304 8mm,换能器中心频率fc=5.0MHz.模型采用文献[22]提供的数字化二维人体腹壁组织图为仿真介质.该腹壁组织结构如图3(a)所示,包含水(W)、结缔组织(C)、肌肉(M)及脂肪(F).各类介质所对应的声学参数已由实验测得(见表1)[17].在此基础上,对声速和密度分别加以幅度为相应物理量平均值3%的随机波动,以在超声传播过程中产生后向散射回波,并在22mm深度处设置充满水的均匀圆形区域作为囊性病变.相对k空间方法仿真的空间采样率要求,原始组织切片图像分辨率相对较低(300dpi),仿真前须对图像进行最邻近点插值以提高空间采样率.仿真时,设定区域的上边界为换能器发射表面,通过水与腹壁组织进行声学耦合;换能器发射信号赋值于y轴方向质点速度采样点,以仿真换能器纵向振动模式;换能器振动信号为加Hanning窗的2周期4MHz正弦信号,换能器振动的最高速度为0.5m/s(可以在焦点处等效产生0.5MPa的空间峰值声压).

表1 腹壁组织声学参数
设定换能器发射焦点距离F=22mm,发射阵元数为32(发射孔径数F/#=2.3),发射线数为32.在仿真聚焦声波传播过程中,同步记录计算区域上边界的声压值作为阵列换能器接收到的回波信号.对回波信号进行波束合成、解调、抽取、对数压缩、双线性插值,获得基频B型超声图像[23],如图3(b)所示.利用Butterworth带通滤波器滤取波束合成信号的二次谐波成分,可获得谐波图像[1],如图3(c)所示.对比图3(b)与(c)可见,谐波成像所获得的囊性暗区边界比基频成像所获囊性暗区边界清晰,验证了谐波成像的优势.由图3(c)可见,谐波成像模式不能对5mm以内的浅层组织良好显像,这是由于超声谐波须在组织中传输一定距离后才能生成,较浅深度范围内回波中的谐波能量仍较弱.
3讨论
本文所述方法使用基于傅里叶变换的k空间算子计算超声非线性方程组中的空间导数(式(8)与(9)),计算精度要高于FDTD中的空间、时间差分运算,因而允许仿真时采用较FDTD方法更低的时间-空间采样率.本文方法还可精确获取超声传播时介质内质点的振动速度,从而可用于超声传播时组织内声强矢量分布和组织升温的仿真计算[24].
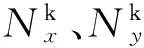

(10)

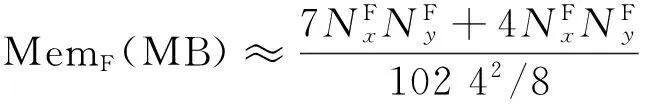
(11)

除与离散傅里叶变换相关运算过程外,式(6)与(7)所描述的迭代步进计算可以在空间各采样点上并行完成.为了展示并行运算对仿真的加速效果,改变2.2节中所述问题的采样点数目,在计算机操作系统中将CPU分别设置为单核与双核运行条件下,测量k空间方法在时间域上单步步进所需的计算时间.测量结果如图4所示,可见随着网格数量(Gsize)的上升,双核对仿真计算的加速效果逐渐明显.尤其是可利用在通用图形处理器(generalpurposegraphicprocessingunit,GPGPU)中运行的并行快速傅里叶变换程序[25],将本文所述方法移植到GPGPU中进一步提高运算速度.
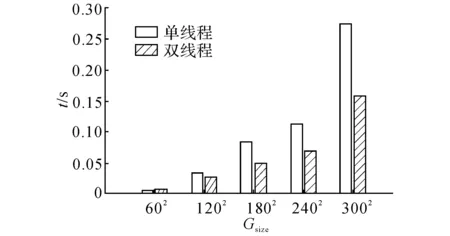
图4 不同矩阵规模下单、双线程程序单步计算时间对比Fig.4 Comparison of compute time between single and double-thread programs under different computation grid sizes
4结语
本文在推导出一阶超声非线性波动方程的基础上,提出了利用k空间方法仿真超声在非均匀组织中传播的模型,同步获得介质内声压与质点振动速度分布情况.与FDTD方法相比,k空间方法能够显著降低仿真时的内存占用量和计算用时.通过仿真声波在一维衰减组织与二维非均匀组织中的传播,验证了k空间方法的准确性,并在此基础上进行了超声谐波成像的仿真.超声谐波成像的仿真结果表明,谐波成像较基波成像能够明显提高深部组织区域的图像质量.
参考文献(References):
[1]SZABOTL. Diagnostic ultrasound imaging [M]. Burlington: Elsevier, 2004:381-428.[2] 周浩, 王友钊, 郑音飞. 医学超声编码激励技术研究进展 [J]. 浙江大学学报:工学版, 2011, 45(2):387-391.
ZHOU Hao, WANG You-zhao, ZHENG Yin-fei. The advance of medical ultrasonic coded excitation [J]. Journal of Zhejiang University:Engineering Science, 2011, 45(2): 387-391.
[3] JI X, BAI J F, SHEN G F, et al. High-intensity focused ultrasound with large scale spherical phased array for the ablation of deep tumors [J]. Journal of Zhejiang University SCIENCE B, 2009, 10(9):639-647.
[4] YING Z M, LIN T, YAN S G. Low-intensity pulsed ultrasound therapy: a potential strategy to stimulate tendon-bone junction healing [J]. Journal of Zhejiang University SCIENCE B, 2012, 13(12): 955-963.
[5] DHANALIWALA A H, HOSSACK J A, MAULDIN F W. Assessing and improving acoustic radiation force image quality using a 1.5-D transducer design [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2012, 59(7): 1602-1608.
[6] VARRAY, F, BASSET O, TORTOLI P, et al. Extensions of nonlinear B/A parameter imaging methods for echo mode [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(6): 1232-1244.
[7] 郑音飞, 邱飞岳, 李鹏, 等. 基于发射束迭代算法的超声波色差抑制方法研究 [J]. 传感技术学报, 2009, 22(2): 240-243.
ZHENG Yin-fei, QIU Fei-yue, LI Peng, et al. Study of reduction aberration of ultrasound image based on iteration of transmit [J]. Chinese Journal of Sensors and Actuators, 2009, 22(2): 240-243.
[8] GJERALD S U, BREKKEN R, HERGUM T, et al. Real-time ultrasound simulation using the GPU [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2012, 59(5): 885-892.
[9] HØILUND-KAUPANG H, MÅSØY S E. Transmit beamforming for optimal second harmonic generation [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(8): 1559-1569.
[10] 吴施伟, 吴海腾, 金浩然, 等. 聚焦探头水浸检测下的频域合成孔径聚焦技术 [J]. 浙江大学学报:工学版, 2015, 49(1):110-115.
WU Shi-wei, WU Hai-teng, JIN Hao-ran, et al. Frequency-domain synthetic aperture focusing technique for immersion testing using focused transducer [J]. Journal of Zhejiang University:Engineering Science, 2015, 49(1):110-115.
[11] VARSLOT T, TARALDSEN G. Computer simulation of forward wave propagation in soft tissue [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2005, 52(9): 1473-1482.
[12] JING Y, CLEVELAND R O. Modeling the propagation of nonlinear three-dimensional acoustic beams in inhomogeneous media [J]. Journal of the Acoustical Society of America, 2007, 122(3): 1352-1364.
[13] 刘伟, 杨军, 田静. 有限振幅波的三维时域建模[J]. 声学学报, 2010,36(4): 349-357.
LIU Wei, YANG Jun, TIAN Jing. Time-domain modeling of finite-amplitude sound beams in three-dimensional Cartesian coordinate system [J]. Acta Acoustica, 2010, 36(4): 349-357.
[14] 解卓丽, 周浩, 郑音飞. 非均匀组织医学超声发射声场仿真. 声学学报, 2013, 38(6):657-662.
XIE Zhuo-li, ZHOU Hao, ZHENG Yin-fei. Simulation of the acoustic field emitted from medical linear transducer in a heterogeneous tissue [J]. Acta Acoustica, 2013, 38(6):657-662.
[15] HALLAJ O, CLEVELAND R O. FDTD simulation of finite-amplitude pressure and temperature fields for biomedical ultrasound [J]. Journal of the Acoustical Society of America, 1999, 105(5):L7-L12.
[16] PINTON G F, DAHL J, ROSENZWEIG S, et al. A heterogeneous nonlinear attenuating full-wave model of ultrasound [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(3): 474-488.
[17] JING Y, WANG T, CLEMENT G T. A k-space method for moderately nonlinear wave propagation [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2012, 59(8): 1664-1673.
[18] TABEI M, MAST T D, WAAG R C. A k-space method for coupled first-order acoustic propagation equations [J]. Journal of the Acoustical Society of America, 2002, 111(1): 53-63.
[19] HAMILTON M F, MORFEY C L. Model equations [M]∥ Nonlinear Acoustics. Melville: Acoustical Society of America, 2008: 41-62.
[20] YUAN X, BORUP D, WISKIN J W, et al. Formulation and validation of Berenger’s PML absorbing boundary for the FDTD simulation of acoustic scattering [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1997, 44(4): 816-822.
[21] BLACKSTOCK D T, HAMILTON M F, PIERCE A D. Progressive waves in lossless and lossy fluids [M]∥ Nonlinear Acoustics. Melville: Acoustical Society of America, 2008: 65-147.
[22] MAST T D, HINKELMAN L M, ORR M J, et al.. Simulation of ultrasonic pulse propagation through the abdominal wall [J]. Journal of the Acoustical Society of America, 1997, 102(2): 1177-1190.
[23] ZHOU H, ZHENG Y F. An efficient quadrature demodulator for medical ultrasound imaging [J]. Frontiers of Information Technology and Electronic Engineering, 2015, 16(4): 301-310.
[24] COX B. Acoustics for ultrasound imaging [EB/OL]. [2015-3-10]. http:∥www.ucl.ac.uk/medphys/staff/people/bcox/bens_lecture_notes.
[25] NVIDIA Corporation. cuFFT [CP/OL]. [2015-3-10]. https://developer.nvidia.com/cufft.
DOI:10.3785/j.issn.1008-973X.2016.03.023
收稿日期:2015-01-04.
基金项目:中央高校基本科研业务费专项资金资助项目(2015FZA5019,2016FZA5015).
作者简介:周浩(1984-),男,博士生,从事医学超声成像技术研究. ORCID:0000-0001-6894-1139. E-mail:bmezhou@zju.edu.cn 通信联系人:郑音飞,男,副教授. ORCID:0000-0001-6837-2634. E-mail:zyfnjupt@126.com
中图分类号:TN 98
文献标志码:A
文章编号:1008-973X(2016)03-06-0574
Simulation of nonlinear ultrasound propagation in heterogeneous tissue
ZHOU Hao, ZHENG Yin-fei
(KeyLaboratoryforBiomedicalEngineeringofMinistryofEducation,ZhejiangUniversity,Hangzhou310027,China)
Abstract:A numerical model was proposed for the simulation of the nonlinear ultrasound propagation in heterogeneous tissue. First, the coupled nonlinear wave equations for pressure and velocity were obtained based on 1-st order nonlinear wave equations in soft tissue to reduce the complexity of numerical computation. Then, k-space method was used to solve the derived nonlinear wave equations to reduce the memory usage and the computation time of the simulation, while preserving the computation accuracy. Compared with the analytic solution of a 1-dimensinal problem and the finite-different time-domain (FDTD) results of a 2-dimensinal problem, and the accuracy of the proposed model was validated. With grid size of 1/9 of the wavelength and Courant-Friedrichs-Lewy (CFL) of 0.3, the square errors of the proposed model and the FDTD method are 0.0125% and 42.5%, respectively. Medical harmonic ultrasound imaging was simulated using the proposed method based on a digital human abdominal map. The results show that image quality can be improved in the deeper tissue by using the harmonic signal.
Key words:nonlinear acoustics; wave equation; medical ultrasound imaging; k-space method; harmonic medical ultrasound imaging
