考虑注浆圈作用水下隧道渗流场解析解

应宏伟, 朱成伟, 龚晓南

(浙江大学 滨海和城市岩土工程研究中心,软弱土与环境土工教育部重点实验室,浙江 杭州 310058)



考虑注浆圈作用水下隧道渗流场解析解

应宏伟, 朱成伟, 龚晓南

(浙江大学 滨海和城市岩土工程研究中心,软弱土与环境土工教育部重点实验室,浙江 杭州 310058)

摘要:总结水下隧道衬砌外水压力以及隧道涌水量的理论研究,采用镜像法构造一个虚拟源,与水下隧道形成“源-汇”系统.将半无限实际渗流场转化为2个无限虚拟渗流场的叠加,推导水下大埋深隧道孔隙水压力以及隧道涌水量的解析解.该解在保证精确性的同时,能考虑注浆圈以及衬砌的作用.在毛洞情况下,本文解退化到古德曼方程以及Harr解,验证了本文解的正确性.采用该解对隧道工程实例进行分析,和已有解进行比较,进一步验证本文解的合理性.发现当埋深增加或者注浆圈抗渗性变差时,已有解和本文解结果差距变大.指出增加注浆圈的抗渗性,可以有效地降低隧道涌水量及衬砌外水头,并发现隧道涌水量及衬砌外水头和隧道埋深近似呈线性增加关系.

关键词：水下隧道；衬砌外水头；涌水量；镜像法；解析解

隧道无论在国民经济还是交通出行方面都扮演着越来越重要的角色.在隧道的设计和建设环节,特别对于高水位山岭隧道以及海底隧道,如何确定衬砌压力和排水量是2个关键问题.实际渗流场求解是一个十分复杂的问题,因为不仅要考虑各种土体参数,还要选择合适的本构关系.事实上,土层中的固相和液相是相互作用的,即所谓的流固耦合.为了使问题简化,大多学者将求解隧道衬砌水压力以及涌水量的问题简化为饱和各向同性、均质的半无限多孔介质土层表面作用一初始水平水位并挖去一个圆形隧道的问题.

Harr[1]基于镜像法原理求得了适用于深埋高水头圆形洞室的围岩孔隙水压力计算公式,该解对高水压深埋隧道孔隙水压力求解计算具有较高的精度.Bobet等[2-3]通过解析模型研究了有水和无水围岩中的衬砌应力,开创了解析法研究不同渗流量下衬砌结构应力的先例.Polubarinova[4]通过假定隧道周围渗流场为稳定流,推导出圆形隧道经常涌水量的近似公式.Kolymbas等[5]在文献[4]的基础上采用复变函数保角映射变换,推导了高水头水下圆形隧道经常涌水量的精确解析解,提出了围岩孔隙水压力分布计算方法.Park等[6-8]利用保角变换,分别将半无限渗流场转化为不同形式的渗流场,并假设不同的边界条件从而获得若干特定情况下的解析解.Joo等[9]利用镜像法求得层流和紊流下隧道渗流量和衬砌外水压力之间的关系,但出现了推导错误.

王建宇[10]假定围岩为各向同性均匀连续介质,将圆形隧道近似为轴对称问题,根据达西定理和无限含水层竖井理论得出涌水量及水压力表达式.王秀英等[11]在文献[10]的基础上,进一步获得山区高水位隧道注浆圈外水头的表达式.李鹏飞等[12-13]结合复变函数和王建宇简化方法,推导由围岩、注浆圈、衬砌混凝土组成的水下隧道渗流场解析解.文献[10-13]均建立在近似解基础之上.谢兴华等[14-17]利用数值法研究了该问题.

综上,在解析解方面,主要存在2种解法,一是复变函数保角变换方法,二是王建宇[10]提出的基于达西定律和无限含水层竖井理论的近似解法.复变函数保角变换方法求解严谨但求解过程较为复杂,且无法考虑注浆圈以及衬砌的作用.文献[10]中的方法简单,可以考虑注浆圈以及衬砌的作用,但因引入了无限渗流边界与实际的半无限边界不符而只能算是近似解.本文将半无限渗流场划分为围岩、注浆圈、衬砌3部分,利用镜像法求解该问题,获得该问题的解析解.

1水下隧道渗流场解析解

1.1计算模型及基本假定

本文研究对象为饱和、均质、各向同性的半无限多孔介质海床,在海床表面作用高度为Hw的水头,并在内部挖去一个半径为rl的隧道；衬砌内半径为r0,渗透系数为kl；注浆圈外半径为rg,渗透系数为kg；隧道中心到海床距离为hc,定义为埋深,海床渗透系数为ks,基准面建立在隧道中心水平面上,如图1所示.区域Ⅰ、Ⅱ、Ⅲ、分别代表围岩、注浆圈以及衬砌.实际工程中,衬砌内部都会设置排水设施,使得隧道内部保持干燥.因此,假定衬砌内部水头为0.

基于以上分析,作以下假定：

1) 围岩、注浆圈、衬砌均质各向同性；

2) 隧道处于稳定渗流状态；

3) 水流服从达西定律；

4) 隧道为大埋深,即rg≪hc；

5) 衬砌内部水头为0.

图1　水下隧道渗流模型Fig.1　Model of seepage around subaqueous tunnel

1.2模型求解

水下隧道半无限渗流场边界条件无法在笛卡尔坐标系或者极坐标系内简单表示,利用镜像法可以简化问题.利用镜像法,将半无限渗流场转化为2个无限渗流场的叠加,如图2所示,实际隧道称为“汇”,对应汇渗流场,而虚构的对称隧道称为“源”,对应源渗流场.r1为任意点M到汇的距离,r2为点M到源的距离.源的出流速度等同于汇的入流速度,根据对称性,可以得到海床面为一个等势面的边界条件.

图2　镜像法示意图Fig.2　Schematic diagram of method of images

当渗流速度较小,处于层流状态时,渗流满足达西定律：v=ki,得

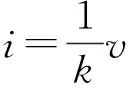
(1)

式中:v为渗流速度,k为渗透系数,i为水力梯度.根据水力梯度以及渗流速度的定义,在区域Ⅰ有

(2)

式中:φ=z+p/γw,为总水头,z为位置水头,p为孔隙水压,γw为水的重度,Q为隧道涌水量(流量以流入为正,流出为负),j=1, 2.对式(2)进行积分,可得

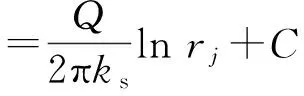
(3)

式中:C为积分常数.

源中心在x=0、z=2hc处,流量为-Q；汇中心在x=0,z=0处,流量为+Q.由式(3)可得区域Ⅰ两个渗流场水头的表达式：

(4)

(5)

式中：φ1为汇渗流场水头,φ2为源渗流场水头,C1、C2为对应的积分常数.

实际渗流场总水头等于φ1、φ2之和,即

(6)

当r1=r2时,即z=hc,φ=H=Hw+hc,故可得

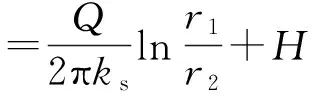
(7)

当r1=rg时,即在区域Ⅰ和区域Ⅱ的交界处,由于rg≪hc,有

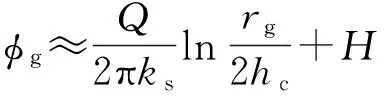
(8)

对于区域Ⅱ和Ⅲ,由于隧道为大深埋,可以认为区域Ⅱ和Ⅲ内渗流为径向流动.

由式(3)可得区域Ⅱ内：

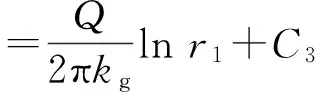
(9)

区域Ⅲ内：

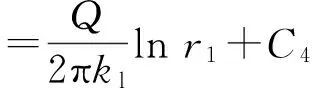
(10)

式中:C3、C4为积分常数.

隧道衬砌内部φ=0,因此

故在区域Ⅲ内：

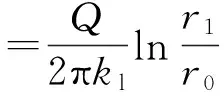
(11)

在区域Ⅱ和Ⅲ界面上,即当r1=rl时,

(12)

代入到式(9)可得

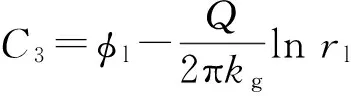
因此在区域Ⅱ内：

(13)

在区域Ⅰ和Ⅱ界面上,即当r1=rg时,

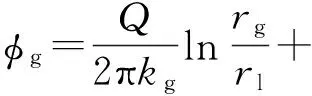
(14)

联立式(8)、(12)、(14)可得

(15)

将式(15)代入式(7)、(11)、(13)，分别得到区域Ⅰ、Ⅱ和Ⅲ内总水头的表达式.

区域Ⅰ：

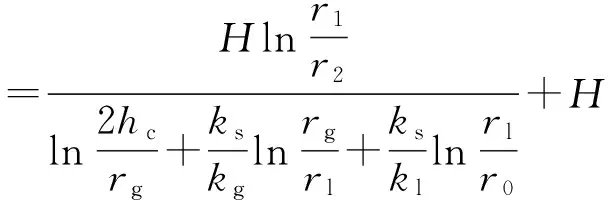
(16)

区域Ⅱ：

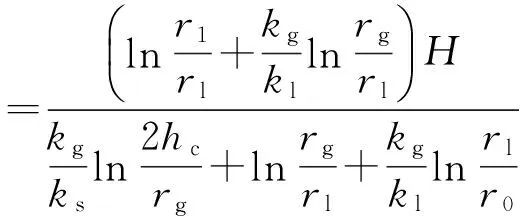
(17)

区域Ⅲ：

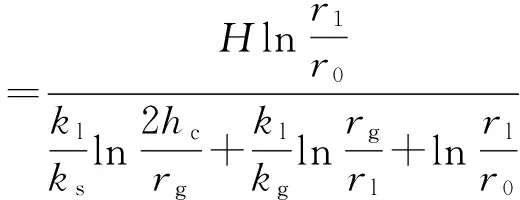
(18)

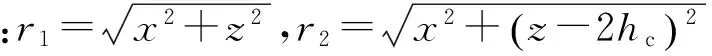
将式(15)代入式(12)和式(14)可得区域Ⅱ和Ⅲ界面以及区域Ⅰ和Ⅱ界面总水头的表达式:

(19)

(20)

则衬砌外水压力为

(21)

注浆圈外水压力为

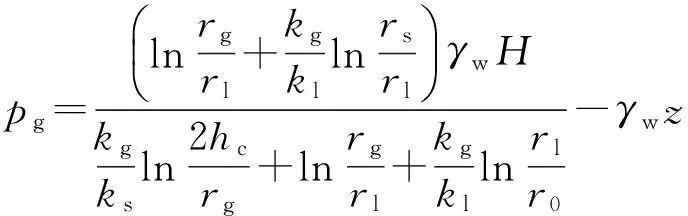
(22)

1.3解的验证

古德曼方程[9]在计算高水头隧道毛洞涌水量时具有非常高的准确度.当隧道为毛洞状态时,认为rg=rl=r0或者ks=kg=kl,此时,式(15)可退化为

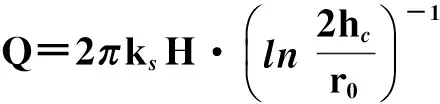
(23)

式(23)即为古德曼自由出流方程.

由式(16)可得毛洞下情况,海床内任意一点的水压力：

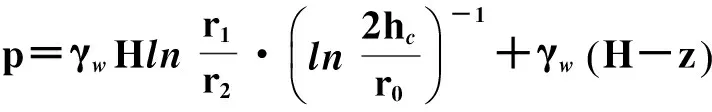
(24)

式(24)即大埋深假定下的Harr解[18].

本文解析解能退化到计算高水头隧道毛洞涌水量的古德曼方程以及水压力的经典解——Harr解,验证了本文解的正确性.

2算例分析

由式(15)可知,影响涌水量的参数可以分为2类,即几何参数hc/rg、rg/rl、rl/r0和渗透系数参数ks/kg、ks/kl.由式(15)可以看出各个几何参数以及渗透系数参数对解析解的影响类似,以下结合算例分别讨论本文解和文献[10]的解的差异,以及埋深和注浆圈渗透系数等参数对解的影响.

某海底隧道工程,衬砌内半径r0=5m,衬砌外半径rl=6m,海床渗透系数ks=5.0×10-6m/s,水深30m,衬砌渗透系数kl=1.0×10-7m/s,注浆圈厚度取4m.定义埋深比nd为埋深和隧道内半径之比,相对渗透系数nk为海床渗透系数和注浆圈渗透系数之比.隧道涌水量及衬砌外水头和埋深比及相对渗透系数的关系如图3～6所示.

图3为隧道涌水量和nk的关系图,图5为衬砌外水头和nk的关系图.由图3和5可知，提高注浆圈的抗渗性能可以有效地降低隧道涌水量以及衬砌外水头,但随着注浆圈抗渗性能的增加,对于隧道涌水量以及衬砌外水头降低的作用趋于平缓.随着埋深的增加,提高注浆圈抗渗性对于降低隧道涌水量以及衬砌外水头作用越明显.图4为隧道涌水量和nd的关系,图6为衬砌外水头和nd的关系,由图4和6可知，隧道涌水量及衬砌外水头随着nd增加而增加,且近似成线性关系.从图3～6还可以看出,文献[10]的解高估了衬砌外水头和隧道涌水量,且随着注浆圈抗渗性的下降以及埋深的增加,文献[10]的解和本文解差距逐渐增大.

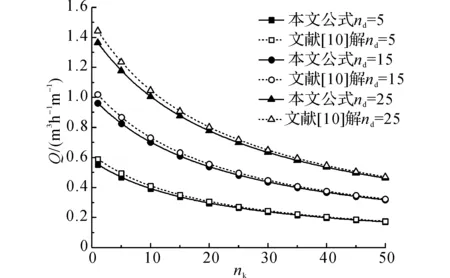
图3　隧道涌水量和注浆圈相对渗透系数的关系Fig.3　Relationship between water inflow of tunnel and relative coefficient of grouting circle permeability

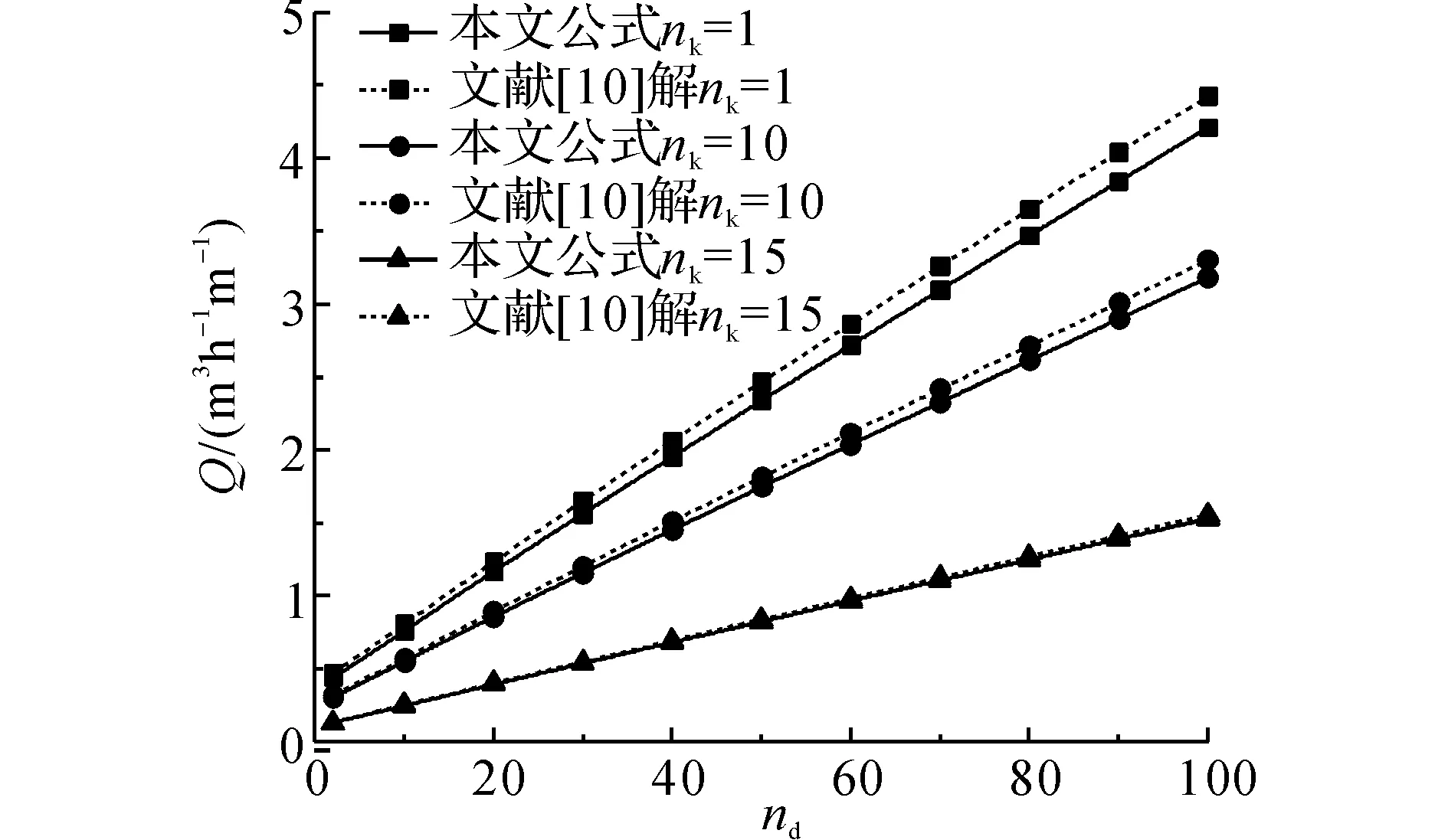
图4　 隧道涌水量和埋深比的关系Fig.4　Relationship between water inflow of tunnel and ratio of burial depth to inner radius of tunnel

图5　衬砌外水头和注浆圈相对渗透系数的关系Fig.5　Relationship between hydraulic head around lining and relative coefficient of grounting circlepermeability

图6　衬砌外水头和埋深比的关系Fig.6　Relationship between hydraulic head around lining and ratio of burial depth to inner radius of tunnel

3工程应用

工程实例一：王育奎等[19]根据相似理论,以某海底隧道右线Ⅳ级围岩中的断面YK6+905为原型,进行模型试验以及数值计算研究.试验参数如下：几何尺寸相似常数为1∶100,重度相似常数为1∶1.33,隧道毛洞半径6.1 cm,上覆土层26.2 cm,海床渗透系数为0.05 m/d,拱顶处水深分别为32.1 cm及44.8 cm.

如表1所示,在不同的水头高度下,无论本文解还是文献[10]的解,相对于模型试验结果或者数值计算结果都偏大,但是本文解比文献[10]的解更加接近试验结果以及数值计算结果.

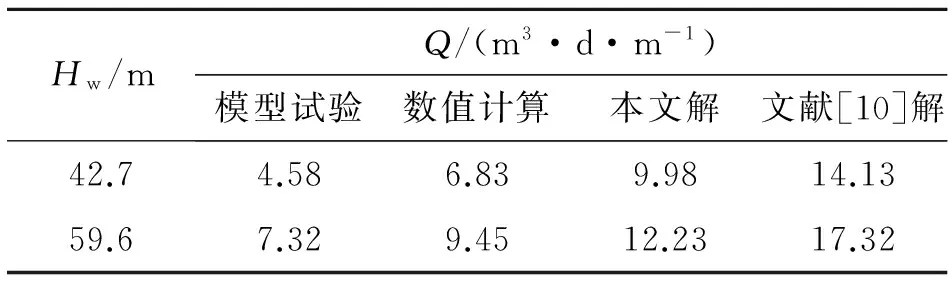
表1　不同方法涌水量值

工程实例二：某海底隧道工程处在断裂破碎带,洞径r0=5 m,衬砌外半径rl=6 m,注浆圈外半径rg=11 m,上覆土层h=30 m,海水深度H=30 m.海床的渗透系数为5.0×10-6m/s,注浆圈的渗透系数为1.0×10-7m/s,衬砌的渗透系数为5.0×10-8m/s.陈俊儒等[20]利用FLAC2D对该工程问题进行数值模拟,得出数值模拟情况下每延米涌水量为3.39 m3/d/m；王建宇解计算结果为3.55 m3/d/m；根据本文解,计算结果为3.50 m3/d/m.

由以上2个工程实例计算结果对比可知,相比较而言,本文解相对于文献[10]解更为合理.

4结论

(1)已有基于无限含水层竖井理论的水下隧道渗流解高估了衬砌外水头和隧道涌水量,随着注浆圈抗渗性的下降以及埋深的增加,已有解和本文解差距变大.

(2)提高注浆圈抗渗性能,可以有效地降低隧道涌水量及衬砌外水压力.

(3)隧道涌水量及衬砌外水压力和隧道埋深比近似呈线性增加的关系.

参考文献(References)：

[1] HARR M E. Groundwater and seepage [M]. New York: McGraw-Hill, 1962: 249-255.

[2] BOBET A. Effect of pore water pressure on tunnel support during static and seismic loading [J]. Tunneling and Underground Space Technology, 2003, 18(4): 377-393.

[3] BOBET A. Analytical solutions for shallow tunnels in saturated ground [J]. ASCE Journal of Engineering Mechanics,2009, 127(12): 1258-1266.

[4] POLUBARINOVA K P Y. Theory of Ground Water Movement [M]. Princeton: Princeton University Press,1962.

[5] KOLYMBAS D, WAGNER P. Groundwater ingress to tunnels: the exact analytical solution [J]. Tunneling and Underground Space Technology, 2007, 22(1): 23-27.

[6] PARK K H, ADISION O, LEE J G. Analytical solution for steady-state groundwater inflow into a drained circular tunnel in a semi-infinite aquifer: a revisit [J]. Tunneling and Underground Space Technology, 2008, 23(2): 206-209.

[7] 皇甫明.暗挖海底隧道围岩稳定性及支护结构受力特征的研究[D].北京: 北京交通大学, 2005.

HUANG Fu-ming. Researsh of excavated rock tunnel stabbility and supporting structure stress characteristics [D]. Bejing: Beijing Jiaotong University, 2005.

[8] 吴金刚,谭忠盛,皇甫明.高水压隧道渗流场分布的复变函数解析解[J].铁道工程学报,2010,9(1): 31-36.

WU Jin-gang, TAN Zhong-sheng, HUANG Pu-ming. Analytic solution of complex function to distribution of seepage field of tunnel with high pressure [J]. Journal of Railway Engineering Society, 2010, 9(1): 31-36.

[9] JOO E J, SHIN J H. Relationship between water pressure and inflow rate in underwater tunnels and buried pipes [J]. Geotechnique, 2014, 64(3): 226-231.

[10] 王建宇.再谈隧道衬砌水压力[J].现代隧道技术,2003, 40(3): 5-9.

WANG Jian-yu. Once more on hydraulic pressure upon linning [J]. Modern Tunneling Technology, 2003, 40(3): 5-9.

[11] 王秀英,王梦恕,张弥.计算隧道排水量及衬砌外水压力的一种简化方法[J].北方交通大学学报,2004,28(1): 8-10.

WANG Xiu-ying, WANG Meng-shu, ZHANG Mi. A simple method to calculate tunnel discharge and external water pressure on lining [J]. Journal of Northern Jiaotong University, 2004, 28(1): 8-10.

[12] 李鹏飞,张顶立,赵勇,等.海底隧道复合衬砌水压力分布规律及合理注浆加固圈参数研究[J].岩石力学与工程学报,2012, 31(2): 280-288.

LI Peng-fei, ZHANG Ding-li, ZHAO Yong, et al. Study of distribution law of water pressure acting on composite lining and reasonable parameters of grouting circle for subsea tunnel [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 280-288.

[13] 杜朝伟,王梦恕,谭忠盛.水下隧道渗流场解析解及其应用[J].岩石力学与工程学报,2011, 30(增2): 3567-3573.

DU Chao-wei, WANG Meng-shu, TAN Zhong-sheng. Analytic solution for seepage field of subsea tunnel and its application [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Suppl. 2): 3567-3573.

[14] 谢兴华,盛金昌,速宝玉,等.隧道外水压力确定的渗流分析方法及排水方案比较[J].岩石力学与工程学报,2002, 21(增2): 2375-2378.

XIE Xing-hua, SHENG Jing-chang, SU Bao-yu, et al. Seepage analysis method for determination of the external water pressure of tunnel and comparison of some drainage schemes [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(Suppl. 2):2375-2378.

[15] 房倩,张顶立,黄明琦.基于连续介质模型的海底隧道渗流问题分析[J].岩石力学与工程学报, 2007,26(增2): 3776-3784.

FANG Qian, ZHANG Ding-li, HUANG Ming-qi.Analysis of seepage problem induced by subsea tunnel excavation based on continuum medium model [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Suppl. 2): 3776-3784.

[16] 许金华,何川,夏炜洋.水下盾构隧道渗流场应力场耦合效应研究[J].岩土力学,2009,30(11): 3519-3527.

XU Jin-hua, HE Chuan, XIA Wei-yang. Research on coupling seepage field and stress field analyses of underwater shield tunnel [J]. Rock and Soil Mechanics, 2009, 30(11): 3519-3527.

[17] 徐帮树,李树忱,李术才,等.海底隧道涌水量和覆岩厚度关系研究[J].力学与实践,2007, 29(1): 34-37.

XU Bang-shu, LI Shu-chen, LI Shu-cai, et al. The relation between seepage volume and rock cover thickness in subsea tunnel [J]. Mechanics in Engineering, 2007, 29(1): 34-37.

[18] 杜朝伟.海底隧道衬砌水压力及结构受力特征研究[D].北京:北京交通大学, 2011.

DU Chao-wei. Research on water pressure on lining and the stress characteristics of lining structure of subsea tunnel [D]. Beijing: Beijing Jiaotong University,2011.

[19] 王育奎,徐帮树,李树才,等.海底隧道涌水量模型试验研究[J].岩土工程学报,2011, 33(9): 1477-1482.

WANG Yu-kui, XU Bang-shu, LI Shu-cai, et al. Laboratory method tests on water flow rate of submarine tunnel [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1477-1482.

[20] 陈俊儒,王星华.海底隧道涌水量的预测及其应用研究[J].现代隧道技术,2008,45(5):18-27.

CHEN Jun-ru, WANG Xing-hua. Prediction and research on water inflow for a subsea tunnel [J]. Modern Tunneling Technology, 2008, 45(5): 18-27.

收稿日期：2015-05-27.

基金项目：国家自然科学基金资助项目(51278462,51338009).

作者简介：应宏伟(1971—),男,副教授，从事岩土工程方面的教学和科研工作. ORCID: 0000-0003-2079-6504. E-mail: ice898@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.06.002

中图分类号：TU 431

文献标志码：A

文章编号：1008-973X(2016)06-1018-06

Analytic solution on seepage field of underwater tunnel considering grouting circle

YING Hong-wei, ZHU Cheng-wei, GONG Xiao-nan

(ResearchCenterofCoastalandUrbanGeotechnicalEngineering,MOEKeyLaboratoryofSoftSoilsandGeoenvironmentalEngineeringofMinistryofEducation,ZhejiangUniversity,Hangzhou310058,China)

Abstract:Summarize the research about the water pressure around the lining and the water inflow into the tunnel. A virtual source was constructed using the method of images, which formed a “source-collection” system together with the under water tunnel. This method can transform the semi-infinite seepage field in reality into the superposition of two virtual infinite ones. The analytic solutions of water pressure around lining and water inflow were derived, considering the effects of the grouting circle and the lining of the tunnel. The solutions could degenerate to the classical Goodman free inflow equation and the hydraulic Harr solution at the condition of unlined tunnels, and were compared with the existing solutions by analyzing two tunnel cases. The study results indicate that the difference between the existing solution and our solution is more significant with a bigger tunnel burial depth or worse grouting circle condition. It is also found that the water inflow and the hydraulic head outside of the lining decrease efficiently with better grouting circle condition. Moreover, the water inflow and the hydraulic head outside of the lining have an approximately linearly increase with the burial depth of the tunnel.

Key words:underwater tunnel; hydraulic head around lining; water inflow; the method of images; analytic solution