中医脉诊的模糊数学处理方法研究
2016-07-31金伟张艳倪家升
金伟,张艳,倪家升
1.山东省中医药研究院,山东 济南 250014;
2.山东省科学院激光研究所山东省光纤传感重点实验室,山东 济南 250014
·专题论坛·
中医脉诊的模糊数学处理方法研究
金伟1,张艳1,倪家升2
1.山东省中医药研究院,山东 济南 250014;
2.山东省科学院激光研究所山东省光纤传感重点实验室,山东 济南 250014
本文针对中医脉诊特征信息处理,研究了模糊数学算法在中医脉诊客观化分析中的应用。通过剖析传统分析方法在中医脉诊中的局限性,给出了模糊数学算法引入的科学根据,并结合实际临床数据,验证了模糊数学算法引入的正确性。
脉诊客观化;模糊数学;金氏脉学
脉诊是中医诊断学的核心内容之一,是数千年来中医诊断的基本手段。由于传统脉诊缺乏客观指标,一直以来各种脉象的辨别依据仅是医生的指下感觉,缺乏统一的客观标准,严重影响了脉诊的准确性。现代科学的突飞猛进,为中医脉诊研究创造了条件,借助先进的电子仪器、计算机技术和生物力学的方法,分析脉象形成的多种因素,将脉象搏动的指感用仪器客观地描记下来,对其进行函数表达和曲线族等量化研究,能较清晰地反映脉象在多维空间的动态变化。迄今为止,虽然在脉诊客观化仪器设备上有了长足进步,但对于脉搏信息的分析处理因缺乏适当的方法论指导,准确性不高。如何对获取的脉搏信息进行合理分析处理,是今后中医脉诊客观化必走之路。
1 传统脉搏信息处理方法及存在的问题
传统脉诊仪通过传感器获取到人体脉搏后,根据传统中医的分析方法进行处理和分析,包括:①时域分析法,主要分析波幅的高度和脉动时相的关系,即脉象图的波、峡的高度、相应时值 t、脉图面积(收缩期面积 As、舒张期面积 Ad),从而了解脉动频率和节律、脉力的强弱、脉势的虚实和脉象形态特征等,但在不同的切脉压力下波形是有变化的,所以,波形不可能包含脉象的全部信息。②频域分析法,即把脉搏波分解成为一系列频率为基本频率整数倍的简谐振动,构成一个频率谱,用频谱与倍频的不同来分析脉象的不同。但脉象波形在频域是否存在更明显特征还处于探索阶段。③速率图分析法。脉象速率图又称为脉象微分图,即波形的微分波。如脉波为压力波时则微分图为dP/dt图形,如脉波为动脉管的位移波时则为位移的微分。④时差图的识别。时差是将心电导联R波叠加于前一心动周期脉图降支上,它可测算从R到脉图起点时间,提示脉搏波传导速度的快慢,血管顺应性如何。⑤自回归-滑动平均模型。这是运用时间序列分析建立的信号回归-滑动平均信号模型,提取波形的特征参数,比较各特征参数的组内离均差与总离均差的比值,然后作F检验、确定判别能力大小进行筛选,利用Bayes准则求判别函数而进行识别。⑥计算机分析。此法是用计算机对脉图进行分析,筛选各项指标,挑出主要指标,运用多因素分析法建立判别及诊断比较。⑦综合性脉象图谱分析法。它是由脉波-脉位趋势图、脉象波形图、脉道形态示意图和脉率趋势图4种图形,加上脉波幅值定标信号构成的中医脉象图谱。
以上分析方法在某些疾病判断上取得一定成果,但大部分方法仍是回到传统中医的老思路上,没有给出客观的量化指标,依然不能称之为真正的客观化;另外一部分过多抛弃了传统脉诊方法,忽视了人体整体性带来的宏观性。
中医传统诊断(指下)与西医最大的区别就是主客观问题,中医往往通过大量的临床经验总结出一套分析方法,且不同的医师分析方法和标准也不同,对疾病的判断并非简单量化可以实现,往往带有“主观感觉”。而西医是根据人体各项具体的指标来判断病症,完全客观化。中医的优点在于考虑到了人的整体性,把人体作为一个有机系统,从而在诊断上能够起到宏观把控的效果;西医的优点在于准确性,依赖先进的医疗设备,对局部病变能够实现高准确度诊断和治疗。中西医优势具有非常明显的互补特性,因此,在中医的客观化进程中,必须既要考虑人体的复杂性,又要借鉴西医判别的客观性,这对于分析算法提出了很大挑战。
2 模糊数学处理方法在金氏脉学中的体现
模糊数学主要是研究没有明确外延的模糊概念的学科,是连接定性和定量之间的桥梁。对一些难以明确量化的概念可以通过模糊数学的处理,使定性的分析转化为定量的分析,对事物给予更严密、更恰当的描述,从而深刻揭示客观事物内在性质和数量之间的规律性,这对脉搏信息的量化处理及脉形的评价具有十分重要的意义。
传统指下号脉过程中,对脉搏判断是依据经验医师的主观判断来确定的,主观判断是存在一定的不确定性或者模糊性的,特别是某些临界值,是与非只是一念间的判断,这就是模糊理论在中医客观化中不可避免的原因。在客观化的脉诊信息处理过程中,某些脉图所属脉象不甚明确,是与否的界限也不很明显,而采用模糊数学的方法,可按模糊理论中的择近原理,将数据进行类比,定出脉象的类型。该方法可避免手指主观感觉的误判,使难以区别的脉象得到较准确的识别。
前期研究通过近30年20万人次的临床实践,笔者确定了脉诊的客观指标,建立了脉诊诊断疾病的数学模型,使脉诊诊断准确率有了很大提高,称之为金氏脉学[1]。但由于脉搏特征(如硬冲搏、软冲搏,致密软涩搏、致密硬涩搏、粘滞性涩搏等)的内涵及外延很难界定,一直影响着脉诊综合诊断的准确性。金氏脉学把这些内涵及外延不分明的特征称为模糊特征。模糊特征在脉学中十分常见,尤其随着脉学研究的深入,构成脉形的元素也愈发复杂。复杂事物有2个突出特点:一是影响该事物的因素众多,人们不可能认识其全部因素,只能在有限的因素上考察事物,由于其他因素的缺乏或丢失,造成本来清晰的现象变得模糊了;二是深度延长(难度增加),这带来了数学模型的复杂化,于是模糊性逐次积累,变得不可忽略,显然传统的集合论对此无能为力。为此,美国计算机与控制论专家扎德(L.A.Zadeh)于1965年提出了“模糊集合论”,并总结出一条互克性原理,即随着系统复杂性的增长,我们对其特性作出精确而有意义的描述能力相应降低,直到达到一个阈值,一旦超过它,精确性和有意义性(或贴近性)几乎成为两个互相排斥的特征[2]。这就是说,复杂程度越高,模糊性越强,精确化程度也就越低,说明模糊性来源于复杂性,解决这个矛盾的有效方法之一,就是在“高复杂性”与“高精度”之间应用模糊数学进行处理。
金氏脉学诊病的依据是脉形。脉形是由特征组成的,理论上组成脉形的特征信息数量越多,对疾病的诊断准确率越高。但事实并非如此,有些脉形特征数量过多,诊断准确率反而降低。其原因是构成脉形的每一个特征在采集识别时都存在着误差参数,所有特征的误差参数组合起来就构成了脉形的总误差参数,故脉形的误差参数与特征的数量正相关。但从另一角度来看,脉形是由许多个特征构成的,简言之,特征数量越多,越会接近理想的脉形特征,即特征数量与脉形的准确性成正比。用数学曲线来分别表现以上两个角度下的误差与特征数量的关系曲线,如图1所示。
从图1可以看出,误差与特征数量呈现出的是两种截然相反的发展趋势,但这两种趋势曲线并不矛盾,而是由于促成机理不同形成的两种趋势,因此,在临床实验中应当中庸地选取特征数量来实现中医的客观化,以找出一个比较合理的特征数量范围。对于脉形分析系统而言,复杂性增长了,准确性和特异性成为了两个反比的特点,这就是互克性原理在金氏脉学中的体现。
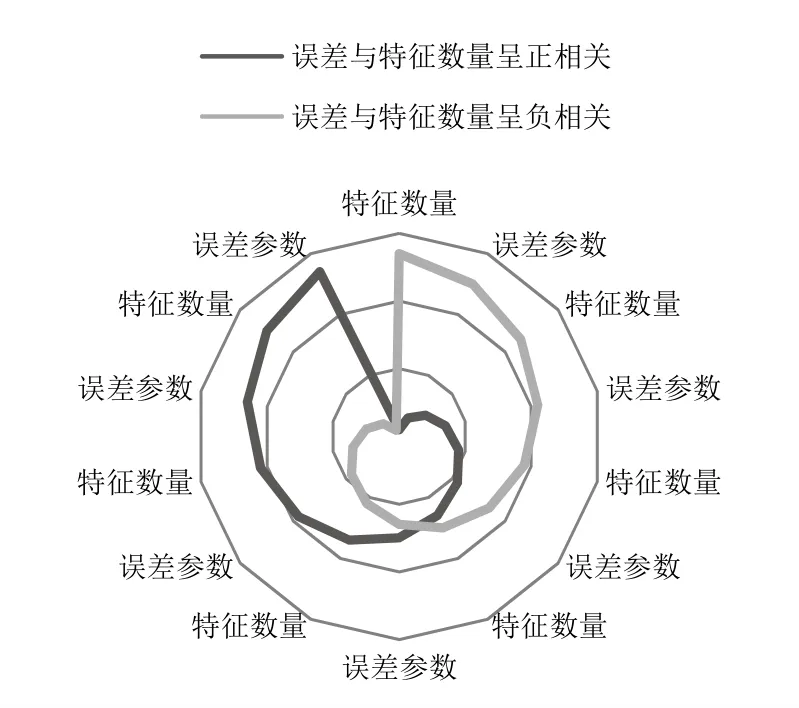
图1 误差与特征数量的两种趋势曲线示意图
2.1 脉病的对应关系
利用模糊数学的论域和模糊子集理论,以脉病的对应关系为论域U,将确定的198种脉形和198种疾病的对应定义为U上的模糊子集A,则U上的元素u对于A的隶属程度可以用隶属度A(u)表示。
从理论意义上讲,人类所有的疾病都应该在脉搏信息上反映出来,并能利用脉学的知识建立起相应的脉形,即为“有其病必有其脉,有其脉必有其病”。一般情况下,建立一个成熟脉形需要经过两个过程,即基本脉形过程和成熟脉形过程。基本脉形过程有两个阶段:第一阶段是试验,这一阶段是从100例已明确诊断的同一种疾病的患者脉搏上寻找特异性特征,如特异性特征达到75%以上就算试验成功。然后进入第二阶段。第二阶段是验证。这一阶段完全使用盲试法,如经50例患者验证特异性特征符合率不低于70%,基本脉形即可建立。基本脉形建立之后,继续用盲试法在临床上做进一步验证,若通过500例患者验证假阳性率不超过30%,才能成为成熟脉形。实际上,由于受患者病种来源的局限及笔者时间精力的限制,更重要的是受人手指触觉敏感性的局限,许多微弱的脉搏信息不能或很难触及和分辨,所以通过近30年的临床实践,才成功建立起了198种成熟脉形,则这198种脉形对A的隶属度为A(u)=1,完全隶属于A;同时,还有部分脉形正在建立中,因病例数还未达到要求,这部分脉形尚待完善,隶属度为0<A(u)<1,在 A(u)的程度上隶属于 A;对许多疾病,笔者在临床中尚未遇到(如艾滋病),无法建立对应的脉形,隶属度为A(u)=0,完全不隶属于A。
2.2 脉形结论与疾病实际的吻合
以脉形和疾病的对应关系为论域U,脉诊结论与病情实际的吻合情况为 U上的一个模糊子集,则 U上的元素u隶属于A的程度可以用隶属度确定。
临床实践中,脉诊确诊率为百分之百的很少,大多数疾病的临床确诊率都达不到百分之百,即0<A(u)<1,在A(u)的程度上隶属于A;没有病理脉形呈现时,A(u)=0,完全不隶属于A。
从临床实际来讲,脉诊确诊率与脉搏清晰度、脉形特异性、特征的稳定程度及采集误差等因素密切相关,而脉搏清晰度、脉形特异性、特征稳定性等又与疾病的轻重程度息息相关,即临床诊断准确率与疾病的轻重程度是正相关的。当机体从亚健康状态刚刚发展进入病理状态时,确诊率低,即A(u)在 0和1之间更靠近0。随着疾病的发展,病情越严重,A(u)的值越靠近1甚至接近1。从另一方面来讲,患者经过及时合理的治疗后,疾病向愈,则 A(u)的值就逐渐离开1向0靠近,疾病痊愈后,A(u)=0,完全不再隶属于A。
2.3 生理信息、中介信息和病理信息
我们设人体脉搏信息的全体为金氏脉学的论域U,病理信息是U上的一个模糊子集A,可以用隶属度来考虑U上的元素u隶属于A的程度。人体脉搏信息分为生理信息、中介信息和病理信息3类。生理信息与病理信息是两个对立的概念,即生理信息完全不属于病理信息,即A(u)=0;病理信息即是其本身,故A(u)=1;中介信息实际上是生理信息和病理信息的过渡状态,体现了生理状态和病理状态相互转化的中间连续变化,是模糊的界定。这时,0<A(u)<1,既不为0(生理信息),又不为1(病理信息)。
机体由健康状态因某些病理因素的作用发展到亚健康状态,脉搏相应呈现出些微特异性变化。脉搏信息从生理信息变化为中介信息,即隶属度从A(u)=0发展到A(u)>0;随着影响因素的增强或机体免疫功能的减弱,脉搏中介信息强度增加,则隶属度从0向1发展,但仍然在0和1之间,只不过隶属于A的程度增加,还没有完全隶属于A;随着影响因素继续增强或机体免疫功能继续减弱,中介信息发展成为病理信息,隶属度达到了A(u)=1,完全隶属于A。反之,当机体呈现为病理状态时,随着及时合理治疗,机体的免疫功能逐渐增强,病理信息开始向中介信息转化,隶属度从A(u)=1退化到A(u)<1;治疗继续进行或机体的免疫功能继续增强,中介信息的强度继续下降,隶属度仍然在0和1之间,隶属的程度减小,还是隶属于A;机体逐渐恢复到健康状态,此时,A(u)=0,中介信息恢复到生理信息,完全不隶属于A。
中介脉形中的直线演变就是隶属度在0和1之间的演变。上线演变是隶属度从0到1的发展,下线演变是从1到0的退化,迂回演变是隶属度的另一种演变形式。上变迂回演变是隶属度从1到小于1再回到1的变化,下变迂回演变是隶属度从0到大于0再恢复为0的演变。
3 小结
脉形是复杂多变的,其变化与许多因素有关,如何评价脉形的好坏优劣,一般的数学方法难以做到。本研究通过模糊数学的综合评判模型考虑各种影响因素的权重来确定脉形适用性的强弱,根据脉形适用性的强弱,判断机体发生某一病变的可能性。所以,模糊数学是从定性到定量诊断的桥梁。
中医脉诊中的模糊数学分析方法融合了中医的整体观、辨证施治的合理性以及西医的具体问题具体分析的辩证法思想,在疾病和呈现于人体脉搏上的信息之间建立了一种映射,通过对脉搏信息的分析处理评价,从而得出与机体状态基本吻合的诊断结论。
笔者已经建立了有关脉形确诊疾病的理论确诊率的公式、肿瘤恶性度判定公式、根据脉形的类权值判断疾病的预向度和实向度,以及计算肿瘤体积、溃疡面大小的数学模型等,这是模糊数学在脉诊理论中可以得到广泛应用的例证。
[1] 金伟.金氏脉学[M].济南:山东科学技术出版社,2000:3-15.
[2] ZADEHL A.模糊集合、语言变量及模糊逻辑[M].陈国权,译.北京:科学出版社,1982:15-27.
Study on Fuzzy Mathematical Algorithm Used in Traditional Chinese Medicine Pulse Diagnosis
JIN Wei1, ZHANG Yan1, NI Jia-sheng2
(1. Shandong Academy of Traditional Chinese Medicine, Jinan 250014, China; 2. The Key Laboratory of Optical Fiber Sensing Technology of Shandong Province, Laser Institute of Shandong Academy of Sciences, Jinan 250014, China)
Targeting characteristic information processing of TCM pulse diagnosis, this article studied the application of fuzzy mathematics in objectifying pulse diagnosis. By analyzing limitations of traditional analytic methods, this article offered the scientific evidence of using mathematical algorithm in pulse diagnosis. At the same time, combined with actual clinical data, it also verified the correctness of introduction mathematical algorithm in TCM pulse diagnosis.
objectifying pulse diagnosis; fuzzy mathematics; Jin's Sphygmology
10.3969/j.issn.1005-5304.2016.06.001
R2-05
A
1005-5304(2016)06-0001-04
2014-01-02)
(
2015-12-18;编辑:梅智胜)
国家科技支撑计划(2012BAI25B04)
