基于合作博弈的大型基础工程各方利益分配机制研究

孙　　蕾，孙绍荣　

（上海理工大学　管理学院，上海　200093，E-mail：telesa_sun@163.com）

基于合作博弈的大型基础工程各方利益分配机制研究

孙蕾，孙绍荣

（上海理工大学管理学院，上海200093，E-mail：telesa_sun@163.com）

摘要：针对大型基础工程中经济利益的分配问题。对地方政府，项目法人和农户3个参与方的收益进行了分析并获得了其利益模型。建立了三方合作博弈模型并分析了其在不同联盟下的利益分配，依据各参与方的收益与其Shapley值分配收益相等的原理，确定了项目法人对地方政府的最佳补偿价格的计算模型及地方政府对农户的最佳补偿价格的计算模型。并利用数值模拟对三方在初始价格下的收益与在最佳补偿价格下的收益进行了比较，结果表明3个参与方之间的补偿价格是决定三方最终收益能否公平合理分配的关键，调整后的补偿价格能够改变利益分配的格局，使利益较为公平合理分配，为有效治理冲突及大型基础工程的顺利实现提供保障。

关键词：合作博弈；利益分配；冲突治理；Shapley值

对于大型基础工程的研究，国外学者主要从经济评估，利益均衡及运行管理等方面对其本国相应的大型基础工程做了较多研究［1，2］，国内学者在对大型基础工程及与土地相关的保障各方利益的研究中，策略型的研究比较多，在针对利益分配的研究中博弈理论被广泛应用，如Wang Xiqin等［3］，马本江等［4］分析了各利益相关者在经济利益博弈模型中的最优策略，王刊良等［5］从微观角度分析了在非对称信息下，农户与地方政府的讨价还价模型，提出了贴现因子等对最后谈判结果的影响。这些策略型研究的前提是参与者具有相同的话语权或者对等的地位，但是在实际问题中对于参与权及话语权有限的农户而言，这增加了在讨价还价中的难度，更难以保证能获得公平合理的经济利益。

合作博弈的理论思想体现了公平与效率，孔祥荣等［6］通过计算按照合作博弈规则划分的运输网络，提出了新型的运输分配方法。Giovanni等［7］从成本分摊的角度研究了合作博弈中参与方的收益问题。Shapley值法作为合作博弈利益分配的优秀机制，应用到许多方面［8～10］。

公平合理的利益分配机制是保证大型基础工程参与主体间合作关系得以发展的关键，也是治理农地冲突的主要内容。孙绍荣等［11，12］通过制度设计来治理不良行为，从行为制度的角度，为某些特定问题提供了治理利益冲突的措施与方法，是对治理利益冲突研究的良好借鉴。

本文以现有的基础工程为研究对象，利用合作博弈的理论从合作的角度为治理农地冲突提供一种新的解决思路和办法，能够改变利益分配的格局，使参与方利益分配相对较为公平合理。

1　基本分析

1.1冲突分析

在土地征收与征用中当农户对利益分配所得产生不满时，地方政府经常会采取拖延与压制措施，这种行为不但不能解决问题反而会引起当事农户的大力反抗，从而引发了许多大规模群体性事件。本文在分析研究大型基础工程中各方利益的基础上拟通过合作博弈的方法与理论，改变不合理的经济利益分配，使各参与方在土地征收与征用过程中都得到合理分配，达成合作，解决上述的冲突（见图1）。

图1　　利益分配与冲突治理关系图　

1.2参与方行为及利益诉求

本文主要分析的参与方行为有地方政府，农户及项目法人。中央政府委托项目法人对重大基础工程进行管理与建设，委托地方政府完成征地与移民等工作及相关政策的落实，往往也会对地方政府的征地行为进行监督，并对违法征地现象进行查处。同时中央政府会出台针对土地征收与征用相应的扶持政策，也会对地方政府进行相应的财政补贴，在中央的税收和补贴下地方政府的收益会提高。地方政府除了落实来自中央政府的政策还承担着组织或协调征地拆迁、移民安置的职责和配套工程建设的组织协调等工作。在现实中征地冲突的对立双方往往是地方政府和失地农民，造成冲突的直接原因多半是地方政府出于自身利益考虑违法强行征地，而农户为了维护自己的土地权益，自发组织起来维权，这是造成冲突引发群体事件的直接原因。

2　大型基础工程参与方利益模型

根据上述对各参与方及相关利益的分析，需建立参与方的利益模型，将模型参数定义如下：

g1：项目法人对地方政府的单位土地补偿价格；g2：地方政府对农户的单位土地补偿价格；g3：项目法人对农户的单位土地补偿价格；k：单位土地价格；RB：项目法人获得的利益；RL：地方政府获得的利益；R3i：农户获得的利益；xi：农户被征收的土地（单位为亩）；（B，L，Pi）：分别表示项目法人，地方政府，参与土地征收及征用的任一农户；δ：中央政府对地方政府的土地征收及征用单位扶持力度即补贴因子；M：预期单位土地工程收益；c：地方政府征地成本费用占补偿金额的比率。

项目法人，地方政府与农户参与的联盟为：｛B，L，1，2，3，…，n｝，1，2，3，…，n代表参与的农户，假设非合作博弈达成的原始分配为：项目法人与地方政府达成的交易价格为g1，地方政府与农户达成的交易价格为 g2。土地价格 的高低取决于可以获取的预期土地收益（地租）的高低和利息率的大小。用公式表示为：土地价格=地租/利息率。k=Q/r。

（1）B（项目法人）所获得的利益。可表示为：

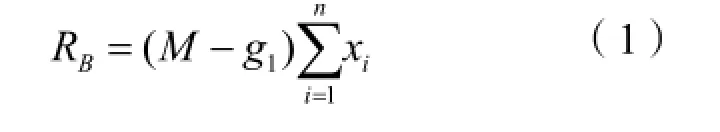
（2）地方政府所获得的利益。可以看作两部分，一部分为得到的上级政府的补贴和政策扶持资金，另一部分为补贴给农户的差价与项目法人的报价差值。

L（地方政府）所获得的利益可以表示为：

式中，g1δ为地方政府获得的来自中央政府的补贴；g1c为地方政府用于土地征收或征用的单位成本费用。

（3）农户所获得的利益。可以表示为：

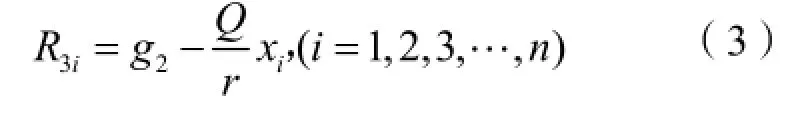
3　大型基础工程经济利益合作博弈模型

设B（N；v）为有n个参与主体的联盟博弈，N=｛1，2，3，…，n｝，P（N）表示参与人集合的所有非空子集的集合，即所有联盟的集合：

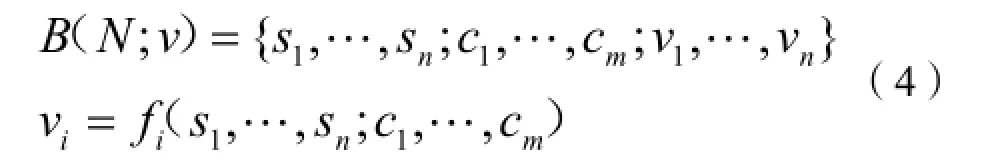
式中，s1，…，sn表示各个参与方的策略空间；c1，…，cm表示参与方联盟所达成的协议；vi表示第i个参与方的特征函数，它是联盟协议和各参与方策略的多元函数；V（S）为联盟保证水平，表示联盟中成员合作时所能获得的最大利益或者节约的成本，V（S）：P（N）→R。

（2）只有地方政府与农户参与的子联盟（L，P1，P2，P3，…Pn）。在该联盟中，地方政府始终参与联盟，农户的参与人数不定。该种联盟能够实现的价值为0。

（3）只有项目法人与地方政府参与的子联盟（B，L）。在该联盟中，由于没有参与征地的农户参与，是没有意义的联盟，因此联盟价值有V（S）=0。

综上，假定每个参与联盟的农户被征地量相等，均为y，单位为亩。则大联盟的总利益v（N）为：

则有：

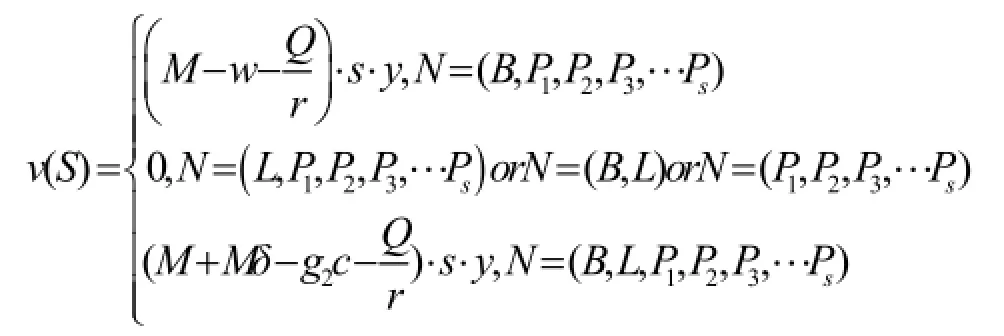
根据以上对三方利益函数的分析，农户的利益为地方政府对其的补偿减去农户本来拥有的土地的价值，项目法人的利益为工程项目的收益减去与地方政府达成的补偿协议，地方政府的利益为与项目法人达成的补偿标准与农户达成的补偿标准的差价加上中央政府的扶持资金与征地成本的差。

4　Shapley值下各参与方利益分配

4.1农户收益分析

考虑农户i参与的联盟，有如下情况：S=｛1，2，3，…，s｝，V（S）=0只有农户参与的联盟，其特征函数为0。

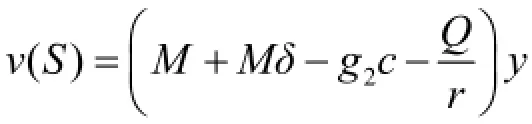
当|S|=4时，联盟S有3种情况：①S=｛B，L，Pi，Pt｝，Pt的选择有，也可以将S的种情况视为一类来处理。，在联盟S中，有两个农户参与其中，因此s=2，Pt，Pk是不同于Pi的任意两个成员，其共有种选择，③S=｛L，Pi，Pt，Pk｝，v（S）=0，v（S｛Pi｝）=0。

当|S|=5时，联盟S有3种情况：①S=｛B，L，Pi，Pt，Pk｝，Pt，Pk的选择有，也可将S的种情况视为一类处理。在联盟S中，有3个农户参与其中，因此s=3，；②S=｛B，Pi，Pt，Pk，Pl｝，Pt，Pk，Pl是不同于Pi的任意三个成员，其共有种选择，，。③S=｛L，Pi，Pt，Pk，Pl｝，v（S）=0，v（S｛Pi｝）=0。

以此类推，当|S|=n+2时，S=｛B，L，Pi，Pt，Pk，Pl…，Pn-1｝，Pt，Pk，Pl…，Pn-1是不同于Pi的其他农户，联盟S共有种，

农户Pi的Shapley值：

4.2项目法人收益分析

考虑所有项目法人B参与的联盟：

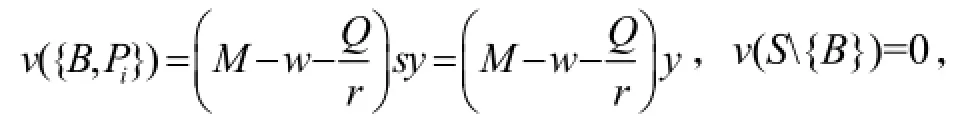
当|S|=4时，有效联盟S=｛B，L，Pi，Pt｝及S=｛B，Pi，Pt，Pk｝①在联盟 S=｛B，L，Pi，Pt｝中 Pt，Pk的选择有，也可以将S的种情况视为同一类来处理。联盟中有两个农户参与其中，因此 S=2，v（S｛B｝）=0，Pi，Pt，Pk｝，Pi，Pt，Pk是任意3个参与联盟的农户成员，其共有种选择，

以此类推，当|S|=n+2时，有效联盟S=｛B，L，Pi，Pt，Pk，Pl，Pn｝，这样的联盟 S共有种，

4.3地方政府收益分析

当|S|=2时，S=｛L，Pi｝及S=｛L，B｝，v（｛L，Pi｝）=0，v（S｛B｝）=0，v（｛L，B｝）=0，v（S｛B｝）=0。

当|S|=4时，有效联盟S=｛B，L，Pi，Pt｝，Pi，Pt的选择有，也可以将S的种情况视为同一类来处理。，在联盟S中，有两个农户参与其中，因此S=2，=

以此类推，当|S|=n+2时，S=｛B，L，Pi，Pt，Pk，Pl，…，Pn｝，这样的联盟S共有种，v（S）=

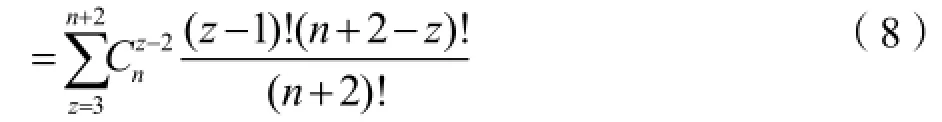
5　最佳补偿价格计算模型

依据参与方利益与Shapley值相等的原理得到如下关系式：

在上述三方利益的分析中每个参与联盟的农户被征地量相等，均为y：

求得：

以上为求得项目法人对地方政府及地方政府对农户的相对合理的土地补偿价格计算模型。根据以上推导结果可以把 Shapley值当做一个反馈机制，计算出能够合理公平进行利益分配的两个补偿价格，在该补偿价格及补贴因子下三方获得的收益与Shapley值分配下的收益相等。

6　数值模拟及结果分析

结合实际调查与访谈将模型参数标准化假设如表1所示。

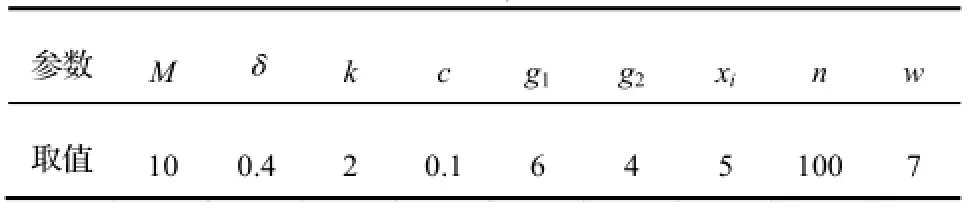
表1　　模型参数设定　

以上参数满足关系式：M＞g1＞g2＞k，δ＞c，

计算给定条件下的补偿价格及补贴因子得：

计算补偿价格调整前的初始分配得：

当补偿价格调整为g1，g2，项目法人、地方政府、农户三方的收益为：

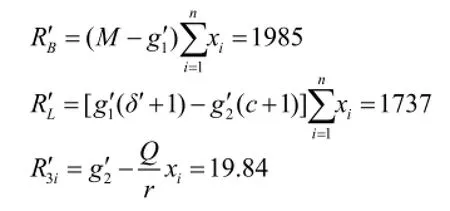
大型基础工程的成本分为两部分，一部分为能够产生效益的成本，如对材料，土地等的投入，称为效益成本。另一部分为不能产生效益的成本为非效益成本，也可称为灰色成本。设工程非效益成本为C，计算调整前的非效益成本，经过调整所得的项目法人对农户的补偿价格g1，地方政府对农户的补偿价格g2，调整后的非效益成本为，显然C2＜C1。

计算结果显示，调整后的非效益成本 C2小于调整前的非效益成本 C1，同时项目法人的收益，地方政府的收益φ′L＜RL，农户的收益，即在其他条件不变的情况下，调整最佳补偿价格后项目法人获得的收益小于初始分配，地方政府获得收益也小于初始分配，农户获得的收益大于初始分配。在非效益成本降低并保证农户收益的基础上，均衡了三方收益，使得地方政府与项目法人的收益均有所下降，其中地方政府的收益大幅下降。

7　结语

3个参与方之间的两个补偿价格是决定最终收益能否公平合理分配的关键，调整项目法人对地方政府的土地补偿价格，及地方政府对农户的补偿价格会改变利益分配的格局，均衡各方收益，使利益的分配相对公平合理，以减少利益方之间的冲突。Shap ley值正好提供了一个合适的方法去确定合理分配下的最佳补偿价格，调整后的价格与补贴因子能够保证在其他条件不变的情况下，实现三方利益合理公平分配。在这种分配机制下保证了在以基层政府为利益权利人的体制下农户的合理利益。为治理农地冲突减少大规模群体事件提供了解决方法，也为提升工程管理水平，为工程实践管理提供科学理论保障，具有一定的现实意义。

参考文献：

［1］Evangelos K Christakos，Glikeria Kalfakakou.An econom ic evaluation model for concession on convention infrastructure projects in Greece［J］.Operational Research，2007，7（1）：147-164.

［2］Ke Yongjian，Liu Xinping，Wang Shouqing.Equitable financial evaluation method for public-private partnership projects［J］.Tsinghua Science and Technology，2008，13 （5）：702-707.

［3］Wang Xiqin，Zhang Yuan，Zeng Yong，et al.Resolving Trans-jurisdictional Water Conflicts by the Nash Bargaining Method［J］.Water Resources Management，2013，27（5）：1235-1247.

［4］马本江，邱菀华.一次交易中的讨价还价策略及其博弈分析［J］.管理工程学报，2005，19（4）：123-125.

［5］王刊良，王嵩.非对称信息下讨价还价的动态博弈：以三阶段讨价还价为例［J］.系统工程理论与实践，2010，30（9）：1636-1642.

［6］孔祥荣，韩伯棠.基于合作博弈的运输分配方法［J］.系统工程理论与实践，2010，30（7）：1340-1344.

［7］Giovanni M Sechi，Riccardo Zucca，Paola Zuddas.Water Costs A llocation in Complex Systems Using a Cooperative Game Theory Approach［J］.Water Resources M anagement，2013，27（6）：1781-1796.

［8］Freixas J.On ordinal equivalence of the Shapley and Banzhaf values for cooperative games［J］.International of Game Theory，2010，39（4）：513-527.

［9］Petrosjan L，Zaccour G.Time consistent Shapley value allocation of pollution cost reduction［J］.Journal of Econom ic Dynamics and Control，2003，27（3）：381-398.

［10］薛俭，谢婉林，李常敏.京津冀大气污染治理省际合作博弈模型［J］.系统工程理论实践，2014，34（3）：810-816.

［11］孙绍荣.行为管理制度设计的符号结构图及计算方法［J］.管理工程学报，2010，24（1）：77-81.

［12］孙绍荣.行为管理制度的失效率治理设计的措施优化组合方法—以工程招投标制度为例［J］.系统工程理论与实践，2012，32（10）：2173-2185.

上海市教委科研创新重点项目（11ZS138）；

上海市哲学社会科学规划课题（2011BGL006）.

中图分类号：F283

文献标识码：A

文章编号：1674-8859（2016）03-088-06

DO I：10.13991/j.cnki.jem.2016.03.015

作者简介：

孙蕾（1990-），女，博士研究生，研究方向：工程管理，行为制度研究；

孙绍荣（1954-），男，教授，博士生导师，研究方向：工程管理，企业管理，行为制度研究。

收稿日期：2016-03-29.

基金项目：国家自然科学基金项目（70871080，71171134）；

Interest Conflict and Governance M echanism of Large Scale Infrastructure Project Based on Cooperative Game

SUN Lei，SUN Shao-rong
（Business School，University of Shanghai for Science and Technology，Shanghai200093，China，E-mail：telesa_sun@163.com）

Abstract：This paper mainly studies conflicts caused by land expropriation and requisition of large scale infrastructure project in china between farmer and government.Cooperative game theory and Shapley Value were used to govern conflict by balance benefit of participants，two com pensation price calculation models were obtained and the calculation result is proved through practical application.First on the analysis of participant's behavior and interests in the implement process of large-scale infrastructure project，and connecting w ith the actual identified three interest models for local government，the project legal person and the farmer's.Established the tripartite cooperation game model under different alliance and studies its interest distribution under the corresponding alliance.Second on the basis of equal princip le betw een participants interest and Shapley value benefit distribution under cooperative game，the best compensation price calculation model for project legal person to local governments and the local government to the farmer's were obtained.At last，by using the numerical simulation of the three parties under the initial price and the best compensation price gains were compared.The result indicates that，two compensation prices of three participants is the key to decide w hether the interests can be allocated fairly and reasonable.The adjusted com pensation price can change the pattern of interests distribution，make sure every participants get a fair and reasonable allocation，that provide realization meaning supporting measures for effective governance conflict in the large-scale infrastructure project in china.

Keywords：cooperative game；benefit distribution；conflict governance；Shapley value