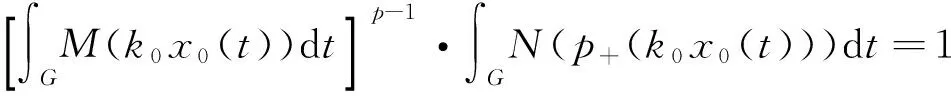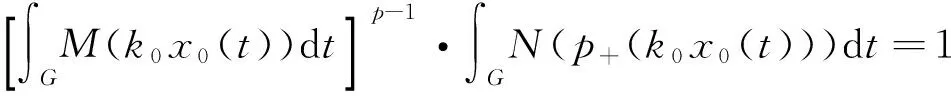赋广义Orlicz范数的Orlicz函数空间的k一致凸点

段丽芬，程亚焕，左明霞

(1. 通化师范学院 数学学院，通化 134002； 2. 哈尔滨理工大学 应用科学学院，哈尔滨 150080)



赋广义Orlicz范数的Orlicz函数空间的k一致凸点

段丽芬1，程亚焕1，左明霞2

(1. 通化师范学院 数学学院，通化 134002； 2. 哈尔滨理工大学 应用科学学院，哈尔滨 150080)

摘要：利用Banach空间基本理论和广义Orlicz范数的特征，研究赋广义Orlicz范数的Orlicz函数空间的局部k一致凸性，得到了由右导函数为连续函数的N-函数所生成的赋广义Orlicz范数的Orlicz函数空间中k一致凸点的判别准则，并且获得该空间局部k一致凸的条件.

关键词：k一致凸点； k一致凸性； 广义Orlicz范数； Orlicz函数空间

k凸性是Banach空间几何学中的重要性质，随着应用范围的扩大，理论研究不断深入[1-5].局部k一致凸(LocalkUniform Rotundity， LKUR)的概念是由Sullivan最先引入的[6]，关于LKUR空间的若干几何性质相继获得[7-9]，赋Orlicz范数和Luxemburg范数的Orlicz空间LKUR的判据也已证明[10-11].本文借鉴文献[10]对赋Orlicz范数Orlicz函数空间k一致凸(kUniform Rotundity， KUR)点判据的刻画思路，针对广义Orlicz范数远远复杂于Orlicz范数的特点，运用特殊的技巧和方法，给出了由右导函数为连续函数的N-函数所生成的赋广义Orlicz范数的Orlicz函数空间中单位球面上的点为k一致凸(KUR)点的判别准则(结论不同于文献[10]赋Orlicz范数的情形)，并据此获得了Orlicz函数空间局部k一致凸的条件(结论相同于文献[10]赋Orlicz范数的情形).

1预备知识

设X是一个Banach空间，X′是其共轭空间，B(X)和S(X)分别表示X的闭单位球和单位球面.

定义1[10]x0∈S(X)称为KUR点是指若

若Banach空间单位球面上每一点都是KUR点，则称X是LKUR的.

定义M(u)的余函数N(v)为

用p+和q+分别表示M和N的右导数.如果存在常数k≥2和x0>0，当|x|≥x0时，满足M(2x)≤kM(x)，则称M满足Δ2条件，记为M∈Δ2.用M∈2表示M的余函数N∈Δ2.设(G，Σ，μ)为一无原子有限测度空间，L0是定义在G上的可测实函数全体，记ρM(x)=∫GM(x(t))dt(x∈L0).Orlicz空间

及其闭子空间

关于Orlicz范数：

Luxemburg范数：

‖x‖M=inf{λ>0：ρM(x/λ)≤1}，

及广义Orlicz范数：

2主要结果

定理1设M是N-函数，p+(u)连续，x0∈S(LM，p)(1

证充分性.由文献[12]定理1可知，条件满足时x0∈S(LM，p)(1

必要性.首先，证明M∈Δ2.若不然，则存在un↑∞，满足

则

注意到

则‖yn‖N，q→‖y0‖N，q=1，故

则

故

又

则

若x0(t)≥0(t∈G0)，取fi： fi(x)=∫Gx(t)χGi(t)dt(∀x∈LM，p)，并记‖fi‖N，q=m0，则

注意到

由定理1立即可得下面的定理.

定理2设M是N-函数，p+(u)连续，则对任何1

参考文献：

[1]SINGER I. On the set of best approximation of an element in a normed linear space [J].RevRoumMathPurApp， 1960，5(2)： 1629-1640.

[2]南朝勋，王建华.k-严格凸性与k-光滑性 [J].数学年刊，1990，11A(3)： 321-324.

[3]冼军，黎永锦.若干k-凸性的等价条件 [J].中山大学学报(自然科学版)，2003，42(1)： 12-15.

[4]SIMSEK N， SAVAS E， KARAKAYA V. On geometrical properties of some Banach spaces [J].AppliedMathematics&InformationSciences， 2013，7(1)： 295-300.

[5]陈利国，罗成，王君.局部凸空间的中点局部k-一致凸性与中点局部k-一致光滑性 [J].中山大学学报(自然科学版)，2013，52(2)： 52-56.

[6]SULLIVAN F. A generalization of uniform rotund Banach spaces [J].CanadJMath， 1979，31： 628-636.

[7]王建华，余健波.LK-UR空间的一些性质 [J].安徽师大学报(自然科学版)，1988(1)： 1-5.

[8]NAN C X， WANG J H. On the Lk-UR and L-kR spaces [J].MathProcCambridgePhilisSoc， 1988，104(3)： 521-526.

[9]HE R Y. The dual properties of LK-UR and k-SS space [J].SoutheastAsianBulletinofMathematics， 2002，26(2)： 215-221.

[10]王廷辅，崔云安.Orlicz空间的K-UR点 [J].黑龙江大学自然科学学报，1995，12(3)： 13-20.

[11]CHEN S T. Geometry of Orlicz spaces [M].Warszawa： Dissertations Math， 1996.

[12]段丽芬，左明霞，王宏志.赋广义Orlicz范数的Orlicz函数空间的UR点和WUR点 [J].中山大学学报(自然科学版)，2014，53(2)： 29-32.

[13]姜镕泽，王俊明，刘复生.赋p-Amemiya范数Orlicz空间的k-端点和k-强端点(1≤p≤∞) [J].哈尔滨理工大学学报，2011，16(2)： 90-93.

k-uniform Rotund Points in Orlicz Function

文章编号：0427-7104(2016)03-0304-06

收稿日期：2014-12-03

基金项目：国家自然科学基金(11226127)；吉林省教育厅“十二五”科技项目(2014-400)；黑龙江省教育厅基金(12531137)

作者简介：段丽芬(1967—)，女，硕士，教授，E-mail： duanlf@126.com.

中图分类号：O 177.3

文献标志码：A

Spaces Endowed with the Generalized Orlicz Norm

DUAN Lifen1， CHENG Yahuan1， ZUO Mingxia2

(1.SchoolofMathematics，TonghuaTeachersUniversity，Tonghua134002，China；2.SchoolofAppliedSciences，HarbinUniversityofScienceandTechnology，Harbin150080，China)

Abstract：Using the fundamental theories of Banach spaces and the characteristics of the generalized Orlicz norm， locally k -uniform rotundity of the Orlicz function spaces endowed with the generalized Orlicz norm is discussed. For the Orlicz function spaces generated by a N-function whose derivative on the right is continuous and endowed with the generalized Orlicz norm， the criterion of k -uniform rotund points in these spaces is presented. And both sufficient and necessary conditions are obtained to make these spaces be locally k -uniform rotund.

Keywords：k -uniform rotund point； locally k -uniform rotundity； generalized Orlicz norm； Orlicz function space