四元数方程AXB+CYD=E通解中复矩阵分量极秩

连德忠，谢锦山，吴敏丽，袁　飞

(1. 龙岩学院 信息工程学院，龙岩 364000； 2. 厦门大学 数学科学学院，厦门 361005)



四元数方程AXB+CYD=E通解中复矩阵分量极秩

连德忠1，谢锦山1，吴敏丽1，袁飞2

(1. 龙岩学院 信息工程学院，龙岩 364000； 2. 厦门大学 数学科学学院，厦门 361005)

摘要：借助四元数矩阵的复表示方式Φ(·)，将四元数体上的线性矩阵方程AXB+CYD=E转换为复数域上的等价复矩阵方程Φ(D)=Φ(E).同时，利用该复矩阵方程的通解和分块矩阵的极秩性质，求出原四元数矩阵方程通解中复矩阵分量集{X0}、{X1}、{Y0}和{Y1}的最大秩、最小秩公式.作为这些极秩公式的应用，推导出了该四元数矩阵方程通解中包含复矩阵解或全为复矩阵解的充要条件.

关键词：四元数； 矩阵方程； 复表示； 分块矩阵； 极秩

在四元数代数理论中，有关四元数矩阵方程通解及其最大秩、最小秩问题，是近年来国内外学者比较关注的热门课题[1-4].由于四元数之间的乘积不可交换，造成四元数体上矩阵之间的运算比复数域上矩阵之间的运算要复杂得多，例如复矩阵常见的基本性质

本文将借助四元数矩阵的复表示，探讨四元数体上常见的一类线性矩阵方程

AXB+CYD=E

(1)

的可解性和通解中的复矩阵分量集的最大秩、最小秩问题，其中，四元数矩阵A、B、C、D、E已知.

A=A00+A01i+A10j+A11k∈Hm×p(A00，A01，A10，A11∈m×p)，

记

A00+A01i=A0∈Cm×p，A10+A11i=A1∈Cm×p，

那么

A=A00+A01i+A10j+A11ij=A00+A01i+(A10+A11i)j=A0+A1j(A0，A1∈Cm×p).

同理，四元数矩阵B、C、D、E，四元数变量矩阵X、Y也可以这样表示.因此，对于每一个四元数矩阵，都可以引进一种等价的复矩阵Φ(·)表示，借助这种复表示，可将矩阵方程(1)转换为等价的复矩阵方程，而该方程的复矩阵解又可以等价映射为矩阵方程(1)的四元数矩阵解.

本文用I代表特定阶数的单位矩阵，分别用R(A)和N(A)表示四元数矩阵A的列右空间和行左空间.由文献[1]可知，dimR(A)=dimN(A)，故将dimR(A)或dimN(A)称为A的秩，并记为r(A).另外，本文沿用A+代表A的莫菲(Moore-Penrose)逆，本文用LA=I-A+A和RA=I-AA+代表由A诱导出的两个算子.

1方程(1)的解集中复矩阵分量极秩

定义1[5-6]对于实四元数体上的任意一个矩阵M=M0+M1j，(M0，M1∈Cm×n)，定义

为矩阵M的复表示矩阵.

依照定义1，不难验证四元数矩阵的复表示矩阵具有以下性质.

引理1[5-6]对于任意矩阵M、N∈Hm×n，

(a) M=N⟺Φ(M)=Φ(N)；

(b)Φ(M+N)=Φ(M)+Φ(N)，Φ(MN)=Φ(M)Φ(N)，Φ(kM)=kΦ(M)(k∈)；

(d) r[Φ(M)]=2r(M)；

(e) [Φ(MH)]=[Φ(M)]H.

引理2[5-6]对于任意矩阵M∈Hm×n，

(a) [Φ(M+)]=[Φ(M)]+；

(b)Φ(RM)=RΦ(M)，Φ(LM)=LΦ(M).

引理3对于任意复矩阵Y∈C2m×2n，存在唯一一个四元数矩阵X∈Hm×n，满足

下面介绍类似于方程(1)的复矩阵方程有解的充要条件，文献[3]中的相关结论在复数域上自然成立.

那么复矩阵方程

(2)

有解的充要条件为

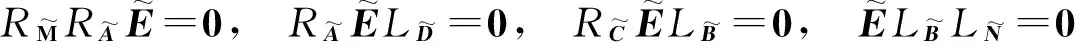
其通解可表示为

本文还用到下列有关分块矩阵秩的引理.

引理5[7-8]设复矩阵A∈Cm×n、B∈Cm×k、C∈Cl×n、D∈Cj×k、E∈Cl×i，那么它们满足：

引理6[7-8]假设复矩阵A∈Cm×n、B1∈Cm×p1、B2∈Cm×p2、C1∈Cq1×n、C2∈Cq2×n都已知，那么

下面，我们考察四元数矩阵方程(1)中的复矩阵解集极秩.

定理1(a) 设四元数矩阵A=A0+A1j∈Hm×p、B=B0+B1j∈Hq×m、C=C0+C1j∈Hm×s、D=D0+D1j∈Ht×n、E=E0+E1j∈Hm×n都已知，那么四元数矩阵方程(1)可解的充要条件是复矩阵方程

(3)

可解；

(b) 如果四元数矩阵方程(1)可解，记

那么

(4)

(5)

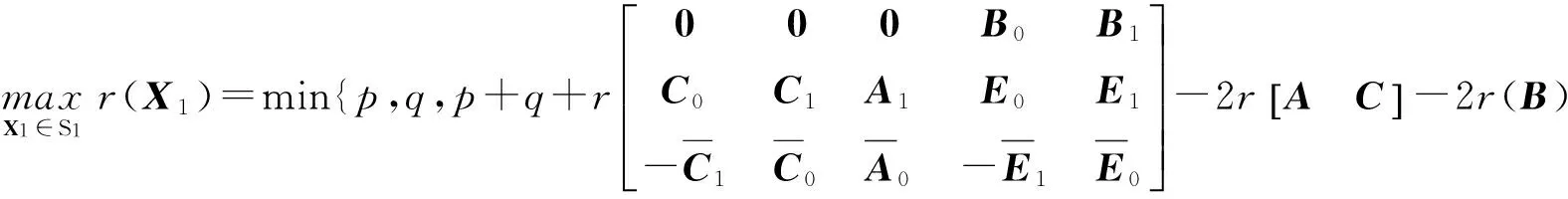
(6)

(7)

(8)

(9)

(10)

(11)

证(a)如果四元数矩阵方程(1)有一对四元数矩阵特解{X0，Y0}，那么{X0，Y0}满足方程(1)，对该等式两边都取四元数矩阵实表示，可得

Φ(A)Φ(X0)Φ(B)+Φ(C)Φ(Y0)Φ(D)=Φ(E).

根据引理1中的性质(c)，可知

即{X0，Y0}就是四元数矩阵方程(1)的一对特解.

(b) 假设四元数矩阵方程(1)有一对特解{X0，Y0}，那么复矩阵方程(3)至少有一对特解{Φ(X0)，Φ(Y0)}.根据引理4可知复矩阵方程(3)的通解为

其中：U∈C2s×2t、V∈C2p×2q、W∈C2p×2q、Z∈C2s×2t、K∈C2s×2t，U、V、W、Z、K为任意复矩阵.

根据引理2的性质可知，

LΦ(A)=Φ(LA)，RΦ(B)=Φ(RB)，

因此，复矩阵方程(3)的通解可表示为：

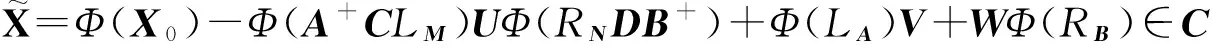
设

由引理3可知

又记

那么

利用引理1的性质(c)，可得

而

即

因此

令

上述各分块矩阵的秩均可按引理5进行化简，其中：

由

MLM=0=RACLM，RNN=0=RNDLB，

可得

AA+CLM=CLM，RNDB+B=RND.

因此

Φ(A)Φ(A+CLM)=Φ(CLM)=Φ(C)LΦ(M)，Φ(RNDB+)Φ(B)=Φ(RND)=RΦ(N)Φ(D).

上述分块矩阵的秩等于

同样的方法可推导出其他分块矩阵的秩：

根据上述结论可证明极秩等式(4)和(5)成立.

用类似的方法可以证明，极秩等式(6)～(11)也成立.

2复矩阵分量极秩的应用

借助定理1，不难判断四元数矩阵方程(1)是否包含复矩阵解、方程(1)的通解是否全为复矩阵解.

(12)

(13)

(b) 如果四元数矩阵方程(1)可解，那么方程(1)所有的解均为复矩阵的充要条件是下列两个秩等式同时成立：

(14)

(15)

四元数矩阵方程(1)所有的解均为复矩阵的充要条件是

由定理1中的极秩等式(6)、(7)、(10)、(11)不难推导出等式(12)～(15).

参考文献：

[1]HUNGERFORD T W. Algebra [M]. New York： Spring-Verlag， 1980.

[2]ZHANG F. Quaternions and matrices of quaternions [J].LinearAlgebraanditsApplications， 1997，251： 21-57.

[3]王卿文，薛有才.体和环上的矩阵方程 [M].北京： 知识出版社，1996： 167-183.

[4]WANG Q W， ZHANG H S， YU S W. On solutions to the quaternion matrix equation AXB+CYD=E [J].ElectronicJournalofLinearAlgebra， 2008，17： 343-358.

[5]JIANG T S， CHEN L. Algebraic algorithms for least squares problem in quaternionic quantum theory [J].ComputerPhysicsCommunications， 2007，176(7)： 481-485.

[6]JIANG T S， ZHAO J L， WEI M S. A new technique of quaternion equality constrained least squares problem [J].JournalofComputationalandAppliedMathematics， 2008，216(2)： 509-513.

[7]TIAN Y G. Completing triangular block matrices with maximal and minimal ranks [J].LinearAlgebraandItsApplications， 2000，321(1-3)： 327-345.

[8]TIAN Y G， LIU Y H. Extremal ranks of some symmetric matrix expressions with applications [J].SIAMJournalonMatrixAnalysisandApplications， 2006，28(3)： 890-905.

[9]连德忠.四元数向量和矩阵的实表示 [J].厦门大学学报(自然科学版)，2003，42(6)： 704-708.

[10]连德忠，袁飞.四元数方程AXAH=B厄米特解中的复矩阵极秩 [J].厦门大学学报(自然科学版)，2014，53(3)： 305-309.

文章编号：0427-7104(2016)03-0288-10

收稿日期：2015-02-09

基金项目：国家自然科学基金(10271099)；福建省科技厅自然科学基金(2015J05010)；福建省教育厅科技A类重点项目(JA14299)；龙岩学院国家基金培育项目(LG2014001)；龙岩学院博士科研启动基金(LB2014018)

作者简介：连德忠(1963—)，男，副教授，E-mail： liandezhong@163.com.

中图分类号：O 151.23

文献标志码：A

Extremal Ranks of Complex Components in General Solutions of Quaternion Equation AXB+CYD=E

LIAN Dezhong1， XIE Jinshan1， WU Minli1， YUAN Fei2

(1.CollegeofInformationEngineering，LongyanUniversity，Longyan364000，China；2.SchoolofMathematicalSciences，XiamenUniversity，Xiamen361005，China)

Abstract：By using a complex representation of quaternion matrix Φ(·)， the linear matrix equation AXB+CYD=E over quaternion field is changed into the matrix equation Φ(D)=Φ(E) over complex field. According to the general solutions of this complex matrix equation and many properties about extremal ranks of block matrix， the maximal and minimal ranks of complex matrices {X0}，{X1}，{Y0}，{Y1} are formulated. These complex matrices are the complex components of the general solutions {X=X0+X1j，Y=Y0+Y1j} of the quaternion matrix equation. As an application， we give the necessary and sufficient conditions for these special cases： (a) There is at least a pair of complex matrices0} in the general solutions of the quaternion matrix equation；(b) All matrices in the general solutions of the quaternion matrix equation are complex.

Keywords：quaternion； matrix equations； complex representation； block matrix； extremal ranks