杏鲍菇切片热风干制数学模型的建立

王存堂，王伟，张雄峰

（1.齐齐哈尔大学食品与生物工程学院，黑龙江齐齐哈尔161006；2.江西省烟叶科学研究所，江西南昌330025）



杏鲍菇切片热风干制数学模型的建立

王存堂1，王伟1，张雄峰2

（1.齐齐哈尔大学食品与生物工程学院，黑龙江齐齐哈尔161006；2.江西省烟叶科学研究所，江西南昌330025）

摘要：研究杏鲍菇切片在不同干制温度（70、80、90℃）和切片厚度（2、4 mm）下的薄层热风干制特性及干制过程数学模型的建立，分析切片厚度和热风干制温度对干制特性的影响。试验结果表明，杏鲍菇切片热风干制的过程以降速干燥为主。杏鲍菇切片热风干制时的水分转移符合Fick's扩散模型。从R2、Χ2和RMSE三个统计数据分析，Page方程模型与杏鲍菇切片干制过程拟合度较高。

关键词：杏鲍菇切片；热风干制特性；薄层干燥模型

杏鲍菇属真菌门、伞菌目、侧耳科，又称刺芹侧耳，是最近几年成功栽培有食用、食疗、药用于一体的珍惜食用菌品种［1］。杏鲍菇营养丰富，含有大量的蛋白质、糖类、碳水化合物、维生素（VC、VB1、VB2）以及钙、镁、锌、铜、铁等矿物质，经常食用杏鲍菇可以降低血液中胆固醇含量，对肝炎、心血管疾病、胃溃疡、糖尿病有一定的治愈及预防作用［2］。新鲜杏鲍菇子实体的水分含量较高，不宜贮藏，在2℃～10℃低温下贮藏保鲜期仅10 d～15 d，其采后保鲜加工成为杏鲍菇产业发展亟待解决的问题［3］。通常果蔬干制有多种方式，如晒干、烘干、减压干制以及冷冻干制等。然而晒干过程容易被微生物污染，产品卫生质量差，质量不均一，烘干和冷冻干燥耗时耗能。为了缩短干制时间，减少营养成分损失和能量消耗，物料切片后再干制被广泛应用在果蔬的脱水干制加工中［4］。果蔬干制过程中水分变化对于干燥过程意义重大，直接影响产品品质。然而限于现代干燥技术，实现物料在干燥过程中在线检测水分仍是个难题，所以对干燥过程中水分的变化规律进行研究将为实际脱水蔬菜的生产提供更多的数据支持。目前，已有学者对苹果［5］、萝卜［6］、大枣［7］等果蔬物料切片的热风干燥特性和动力学模型进行了研究。然而关于杏鲍菇切片热风薄层干制数学模型方面的研究鲜见报道。因此，在本试验研究中将杏鲍菇切片处理后在进行热风干制，考查杏鲍菇切片热风干制温度和切片厚度对干制特性的影响并建立干制过程的数学模型，期望为生产加工实践提供基础数据支持。

1　材料与方法

1.1试验材料

新鲜杏鲍菇：购于齐齐哈尔农贸市场，选择成熟度七八成、果型大、具有典型杏鲍菇风味、果肉具有一定硬度的杏鲍菇。

1.2主要仪器设备

数显101A-2型电热鼓风干燥箱：上海浦东荣丰科学仪器有限公司；BS222S电子天平：赛多利斯科学仪器（北京）有限公司。

1.3方法

在干制试验开始之前2 h，将热风干燥箱开机并选定温度。在获得稳定的干制条件后，将杏鲍菇清洗后垂直与长轴方向分别切成2 mm厚和4 mm圆形薄片。准确称取200 g杏鲍菇切片，单层平铺置于铁丝网上在电热鼓风干燥，干制试验开始。干制温度分别为70、80、90℃，风速恒定为1.0 m/s。每隔10 min记录一次重量变化（水分损失情况），精确至0.01 g，每次称重不超过20 s，直至连续3次重量不在变化为止。所有的干制实验重复3次。

1.4热风干制特性

1.4.1数学模型

杏鲍菇薄层干制试验的水分比（Moisture Ratio：MR）和干制速率（Drying Rate：DR）分别采用方程（1）和（2）计算：

以上方程中各字母表示如下，均为干基含水率，以每克干重计：M为任意时刻的水分含量，（g/g）；M0为初始水分含量，（g/g）；Me为平衡水分含量，（g/g）；Mt为t时刻的水分含量，（g/g）；Mt+dt为t+dt时刻的水分含量，（g/g）；t为干制某一时刻t，min。

当干制时间较长时，与M或M0相比，Me的值比较小，可以忽略不计［5］。所以：MR=M/M0。

1.4.2相关系数和误差分析

为了选择合适的数学模型描述杏鲍菇切片的干制过程，本研究利用理论模型-扩散模型和常见的5个经验薄层干制模型方程来分别描述杏鲍菇切片的干制曲线［5-7］。见表1。

表1　杏鲍菇干制使用的经典薄层干制数学模型Table 1　Thin-layer drying models used for mathematical of drying of pleurotus eryngii slices

采用OriginPro8.5数学统计软件分析线性和非线性回归方程，并给出各统计参数如相关系数（R2），卡方（Χ2）和均方根误差（root mean square error，RMSE）。最好的描述物料薄层干制模型的统计分析参数是R2最大，并且Χ2和RMSE最小。Χ2和RMSE根据以下方程计算：

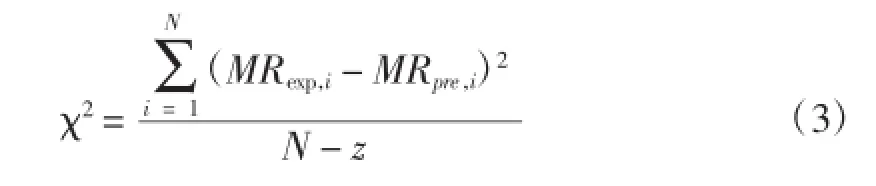
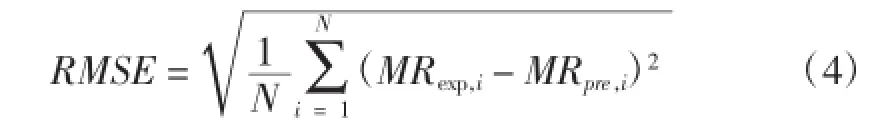
在上述方程中，MRexp，i和 MRpre，i分别为试验的MR和预测的MR，N为观测点的数量，z为干制数学模型中常数的数量。

2　结果与讨论

2.1干制特性曲线

干制特性曲线是MR与干制时间之间的关系曲线，它表明了物料水分含量随干制时间的延长而逐渐下降的过程。杏鲍菇在不同干制温度，不同切片厚度下的MR与干制时间之间的关系曲线见图1。

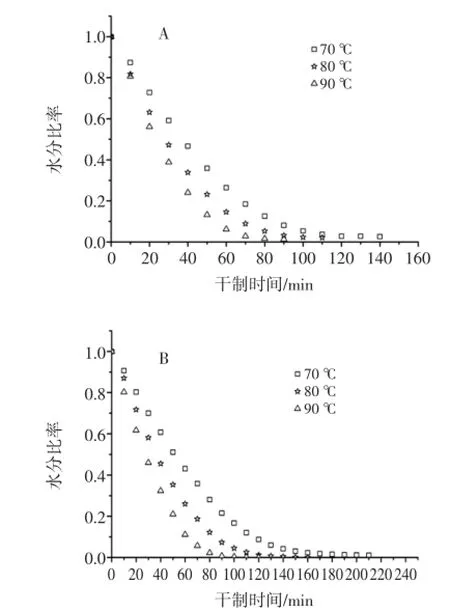
图1　 杏鲍菇不同干制温度和切片厚度（A：2 mm；B：4 mm）下的热风薄层干制曲线Fig.1　Thin-layardryingcurvesofpleurotuseryngiisliceatdifferent temperature for sample thickness of（A）2 mm and（B）4 mm

由图1可知，MR随干制时间延长而逐渐下降。热风温度与切片厚度对干制时间的影响是显著地。在干制温度分别为70、80、90℃干制条件下，切片厚度2 mm杏鲍菇获得平衡水分的时间分别为140、110、90 min，而切片厚度4 mm杏鲍菇获得平衡水分的时间分别为210、160、110 min。在选定的干制温度下（70、80、90℃），提高热风温度和减小切片厚度都使干制时间缩短。在干制温度分别为70、80、90℃时，切片厚度2 mm的杏鲍菇是切片厚度4 mm的杏鲍菇干制时间的67%、68%、81%，很明显温度一定时切片厚度越大干制时间越长。这是因为切片厚度小，水分蒸发时转移距离缩短和单位质量样品蒸发面积增加导致的［8］。相似的结果在梨切片干制［9］和番茄切片干制［10］时也被报道。

2.2干制速率曲线

杏鲍菇切片热风干制速率根据方程（2）计算。对于切片厚度分别是2 mm和4 mm的切片，其干制速率随水分含量的变化见图2（A：2 mm）和（B：4 mm）。

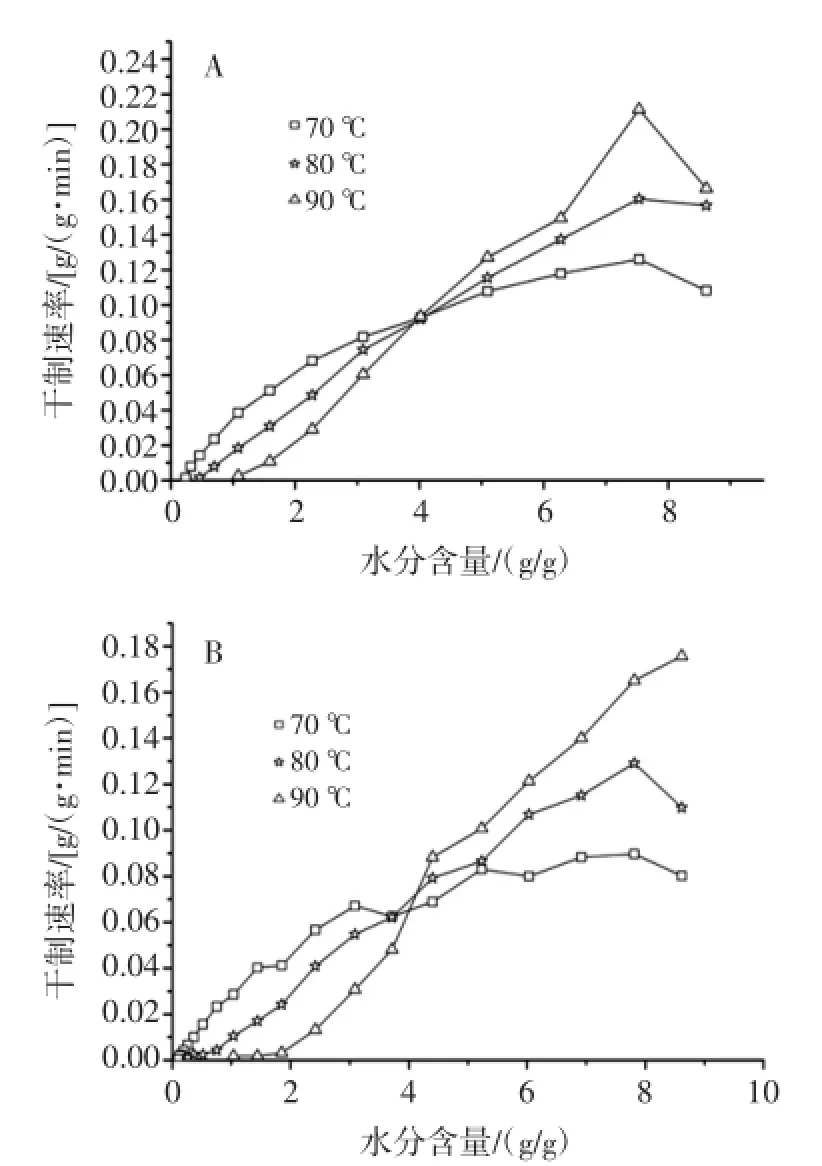
图2　杏鲍菇切片不同干制温度和不同切片厚度（A：2 mm；B：4 mm）下的干制速率-水分含量曲线Fig.2　Dryingrateversusdryingtimeofpleurotuseryngiiatdifferent temperatures for sample thickness of（A）2 mm and（B）4 mm

从图2中可以看出杏鲍菇的干制速率随水分含量的持续下降而降低。同时也可以看出，当热风温度升高，并且切片厚度减小时，干制速率也随之增加。在切片厚度分别为2 mm和4 mm；杏鲍菇水分含量大于1.0 g水/g干物质和0.7g水/g干物质时，干制温度越高，干制速率越大；而当杏鲍菇水分含量小于1.0 g水/g干物质和0.7g水/g干物质时，干制温度越高，干制速率越小。这说明在切片厚度相同时，在干制后期，水分含量越低时，干制的速率越小，水分越难以除去。有许多研究也报道，在干制后期，采用其他干制方式如微波干制处理，加快后期水分蒸发的速率，从而缩短干制的时间［11］。

2.3杏鲍菇切片热风干制数学模型

干制试验的水分含量数据可以转化为含水率，然后根据方程（1）计算MR，作为模型拟合的原始数据。然后根据表1的经验薄层干制方程模型拟合，从而选择合适的杏鲍菇干制模型。根据不同模型的统计结果以及R2，Χ2和RMSE的值，得出拟合度较高的数学模型（表2）。评价标准如下：最好的薄层干制模型要求最高的R2，最低的Χ2和RMSE的值。对于所有的干制实验，其R2，Χ2和RMSE的值变化范围分别为0.988 7～0.999 7，0.000 012～0.001 132，0.004 1～0.033 7。

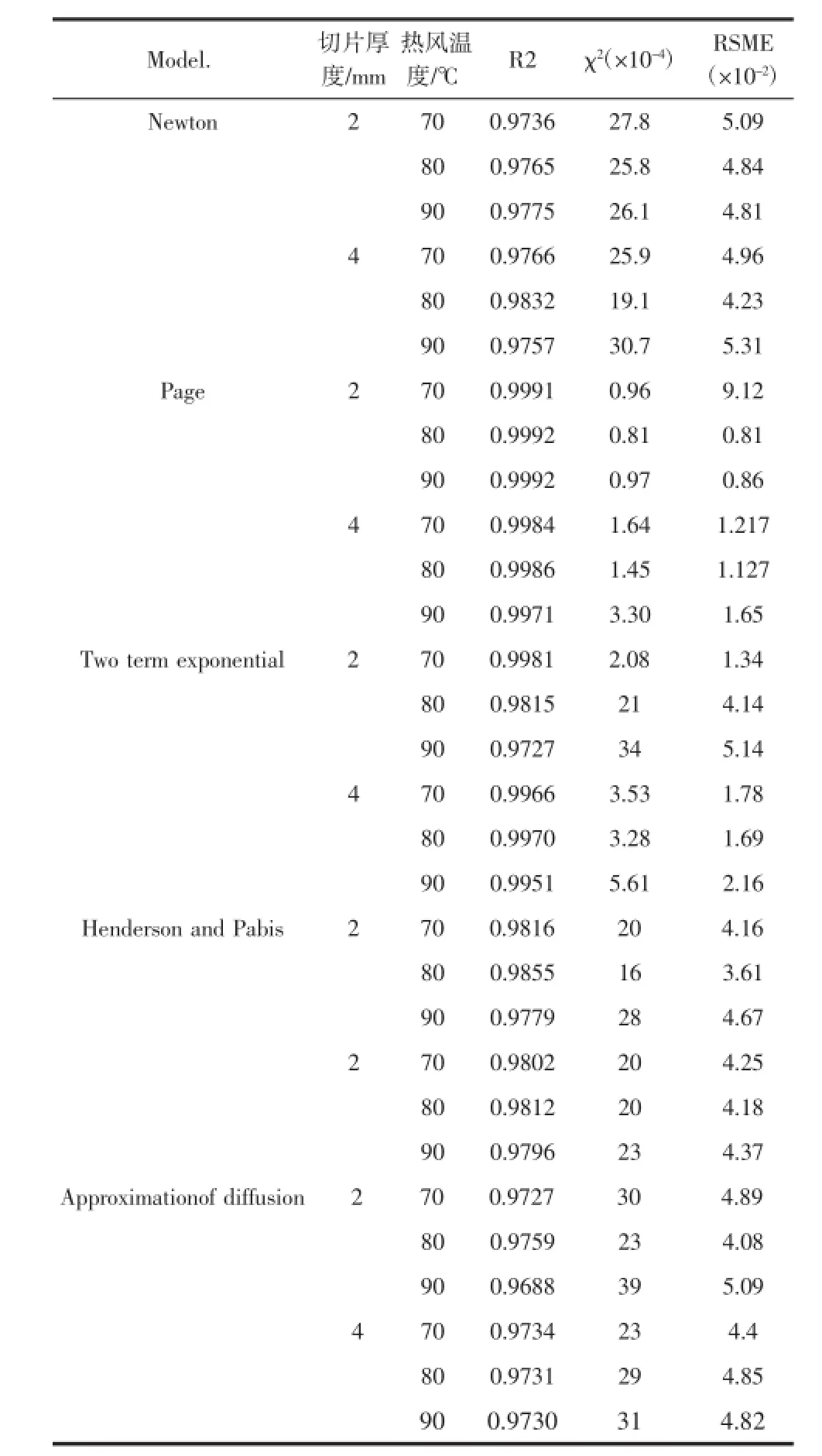
表2　不同薄层干制模型所模拟的统计结果Table 2　Statistical results obtained from various thin-layer drying models

从表2可知，从Page方程模型计算得到的R2最大，Χ2和RMSE最小，拟合度较高，能很好的描述杏鲍菇的薄层干制过程。

2.4杏鲍菇切片热风干制数学模型的验证

杏鲍菇切片热风干制数学模型的验证图见图3。

图3　对比Page模型下不同干制条件时的实验的MR和预测的MRFig.3　Comparison of experimental and predicted moisture ratio by the page model for various drying condition

由图3可以看出，杏鲍菇切片不同厚度试验MR与预测的MR是一条大约45°的直线。这就说明Page模型能很好的描述杏鲍菇热风干制的过程。其他研究者也报道Page模型能很好的描述热风干制过程，如番茄切片［10］，苹果切片［12］的热风干制模型等。

杏鲍菇切片热风薄层干制的预测模型Page方程的参数见表3。

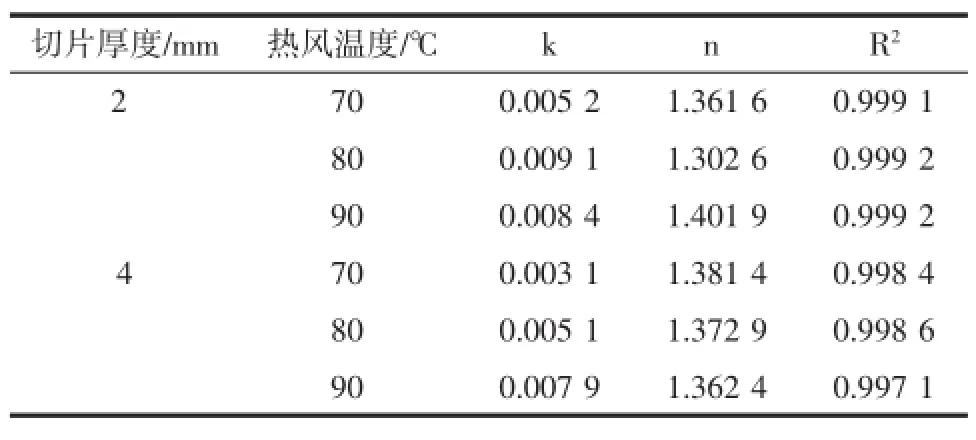
表3　杏鲍菇切片热风薄层干制Page方程不同温度和切片厚度下的模型参数Table 3　Estimated values of parameters of page model used for thin-layer drying of pleurotus eryngii slices at different sample thicknesses and temperatures

3　结论

1）热风温度、切片厚度对杏鲍菇切片薄层热风干燥特性的影响是显著的。在试验温度范文内，热风温度越高、切片越薄，杏鲍菇切片的干燥速率越快，干燥时间越短。

2）杏鲍菇切片薄层热风干燥过程只有开始时短暂的升速阶段，其后为降速干燥阶段，没有恒速阶段。

3）经验数学模型的拟和结果表明，Page模型拟和优值最好，R2值最高，Χ2和RMSE最小，是描述杏鲍菇切片薄层热风干燥过程最适合的数学模型，该模型能准确地表达和预测杏鲍菇切片薄层热风干燥过程中不同条件的任一时刻的水分含量和干燥速率。

参考文献：

［1］邢淑婕，刘开华.不同干制方法对杏鲍菇品质的影响［J］.食用菌学报，2010（17）1：83-85

［2］陈健凯，林河通，李辉，等.杏鲍菇的热风干燥特性与动力学模型［J］.现代食品科技，2013，29（11）：2692-2699

［3］陈健凯，林河通，李辉，等.杏鲍菇微波真空薄层干燥数学模型建立与评价［J］.真空科学与技术学报，2013，33（12）：1184-1190

［4］Zafer E，Filiz I.A review of thin layer drying of foods：theory，modeling，and experimental results critical［J］.Reviews in Food Science and Nutrition，2010，50（5）：441-464

［5］Antonio VG，Kong AH，Marcelo C，et al.Effect of temperature and air velocity on drying kinetics，antioxidant capacity，total phenolic content，colour，texture and microstructure of apple（var.Granny Smith）slices［J］.Food Chemistry，2012，132（1）：51-59

［6］Jun Ho Lee，Hui Jeong Kim.Vacuum drying kinetics of Asian white radish（Raphanus sativus L.）slices［J］.LWT-Food Science and Technology，2009，42（1）：180-186

［7］Jun H L，Li Z.Mathematical modeling on vacuum drying of Zizyphus jujubeMiller slices［J］.Journal Food Science Technology，2013，50（1）：115-121

［8］Sacilik K and Elicin AK.The thin layer drying characteristics of organic apple slices［J］.Journal of Food Engineering，2006，73：281-289

［9］DoymazI and I.smail O.Experimental characterization and modelling of drying of pear slices［J］.Food Science and Biotechnology，2012，21 （5）：1377-1381

［10］Engin D，Tulek Y.Thin-layer drying of tomato（Lycopersicum esculentum Mill.cv.Rio Grande）slices in a convective hot air dryer ［J］.Heat and Mass Transfer，2012，48（5）：841-847

［11］Arikan M F，Ayhan Z，Soysal Y，et al.Drying Characteristics and Quality Parameters of Microwave-Dried Grated Carrots［J］.Food and Bioprocess Technology，2012，5（8）：3217-3229

［12］Menges H O.and ErtekinC.Mathematical modeling of thin layer drying of Golden apples［J］.Journal of Food Engineering，2006，77 （1）：119-125

DOI：10.3969/j.issn.1005-6521.2016.11.008

基金项目：齐齐哈尔大学青年教师科研启动支持计划项目（2014K-M25）

作者简介：王存堂（1980—），男（汉），副教授，博士，主要从事农产品贮藏及加工方向的研究工作。

收稿日期：2015-04-27

Mathematical Modeling on Hot-air Drying of Pleurotus eryngii slices

WANG Cun-tang1，WANG Wei1，ZHANG Xiong-feng2

（1.College of Food and Biological Engineering，Qiqihar University，Qiqihar 161006，Heilongjiang，China；2.Tobacco Research Institute of Jiangxi Province，Nanchang 330025，Jiangxi，China）

Abstract：Pleurotus eryngii slices were dried as thin-layers with thickness of 2 mm and 4 mm in the ranges of 70℃-90℃of drying hot-air temperature in a convective dryer.The effect of drying hot-air temperature and slice thickness on the drying characteristics was analyzed.Resultsindicated that drying took place in the falling rate period.Moisture transfer from Pleurotus eryngii slices was described by applying the Fick'sdiffusion model. A non-linear regression procedure was used to fit eight thin-layer drying models available in the literature to the experimental moisture loss data.The mathematical models comparedaccording to the three statistical parameters such as the coefficient of determination（R2），reduced chi-square（Χ2）and root means squareerror（RMSE）be

tween the observed and predicted moisture ratios.In conclusion，the Pagemodel satisfactorilydescribed the dry

ing characteristics of Pleurotus eryngii slices.

Key words：Pleurotus eryngii slice；hot-air drying characteristic；thin layer drying model