结构设计参数对轮胎振动噪声的影响

安登峰，赵 璠，王国林

（1.北京橡胶工业研究设计院，北京 100143；2.江苏大学 汽车与交通工程学院，江苏 镇江 212013）

高速行驶时的轮胎噪声已成为汽车噪声的主要来源。为限制轮胎噪声，欧盟、美国、日本、韩国、巴西等相继出台了轮胎标签法规，对轮胎噪声提出了明确限值要求。国际轮胎法规政策日益严苛，而国内先进轮胎技术匮乏，严重影响我国轮胎产业在世界市场角逐的竞争力，因此低噪声轮胎结构设计新技术研究迫在眉睫。

研究表明，以纵向花纹沟槽为主的载重子午线轮胎在行驶过程中的花纹噪声较小，结构振动辐射噪声起主要作用[1]。轮胎振动辐射噪声的产生分为振动激励、振动响应和声辐射3个阶段。S.K.Byoung[2]根据Boehm提出的子午线轮胎薄壳运动方程得到胎体振动方程，求得胎面径向位移，从而计算出胎体振动辐射的比声压。V.Q.Doan等[3]通过试验和有限元分析证明了噪声与胎面振动的关系，研究了结构改变对胎面振动的影响。包秀图[4]分析了不同工况和结构参数对轮胎振动噪声的影响。石焕文等[5]分析了轮胎辐射声场的特征，求解了轮胎在径向激励力作用下的辐射效率、辐射声功率、表面振动速度及轮胎声场指向性。周海超等[6]利用正交试验方法研究了使用因素对子午线轮胎噪声水平的影响。

国内外学者已从理论分析、有限元方法及试验等方面对轮胎的振动辐射噪声进行了深入研究，但目前尚未形成较为完善的理论与方法。基于声传递向量（Acoustic Transfer Vector，ATV）和模态声学传递向量（Modal Acoustic Transfer Vector，MATV）的振动噪声分析方法已在汽车行业得到广泛应用，但采用MATV方法对轮胎振动辐射噪声进行预测则鲜有报道。

本工作以载重子午线轮胎295/80R22.5为研究对象，利用Abaqus软件建立有限元分析模型，结合声学边界元理论，采用MATV方法计算轮胎在滚动过程中的振动辐射噪声，利用轮胎外轮廓声学贡献度方法，分析水平轴位置和加强层高度对振动噪声性能的影响。

1 理论基础

1.1 ATV方法

ATV是系统的固有属性，表征结构表面法向振速与场点声压之间的关系，其物理意义为单元或节点在特定频率下的单位速度在场点上引起的声压值[7]。当压力扰动较小时，声学方程可看作线性的，在系统的输入和输出之间建立一种线性关系。如将结构表面离散为有限个单元，则在声场某点处的声压可表示为

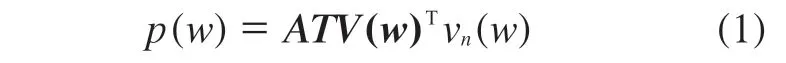
式中，p为空间某一位置处的声压，v(w)n为结构表面的法向振动速度，ATV(w) 为声传递向量。声压取决于振动表面的几何形状、声传递介质的物理属性、声学响应的场点位置和分析频率等，与振动结构的载荷和结构响应无关。

1.2 MATV方法

MATV的物理意义可理解为单元或节点在特定频率下由单位模态响应在声场某点处引起的声压值[8]。其中，模态参与因子表征的是模型的模态与场点声压的关系。轮胎各阶模态乘以相应的权重系数，继而叠加，形成声压波动。MATV方法是用模态和模态参与因子表示振动，即：

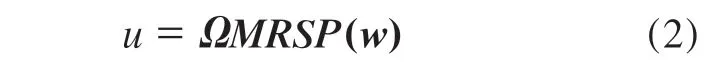
式中，u为结构位移，Ω为结构模态向量组成的矩阵，MRSP(w) 为模态参与因子组成的向量。

将结构位移向量投影到结构表面法线方向，即可得结构在法线方向上的振动速度：

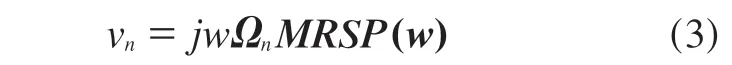
式中，Ω n为结构振动模态在结构表面法线方向的分矢量组成的矩阵，j为虚数单位，w为频率，声场任意点处的声压为

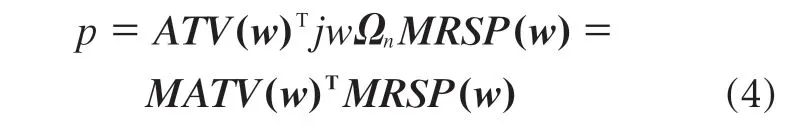
式中，MATV(w)T为模态声传递向量。

MATV方法不依赖于工况，效率更高，与结构的几何形状、分析频率、声介质的物理参数和结构模态形状等参数有关。

1.3 声学边界元求解方法

采用声学边界元法求解声压，考虑了轮胎与路面的接触过程，对模拟轮胎/路面相互作用产生的轮胎振动辐射噪声具有较高的计算精度[9]。

在三维直角坐标系中，波动方程可写为

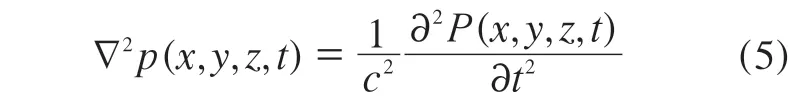
式中，∇表示劈形算符，c表示声速，t表示时间。

令p(x,y,z,t) =p(x,y,z) ejwt，得到声学Helmholtz方程：

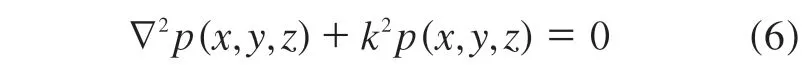
其中，k=w/c。

声学方程的基本解为

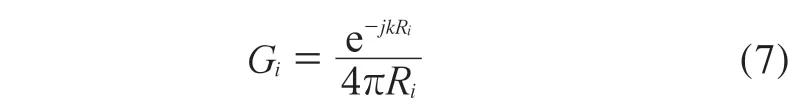
式中，Gi为格林函数的基本解，Ri表示声源点到观测点之间的距离。

结合Helmholtz方程和格林公式，可得Vi外部空间点处声压的积分方程：

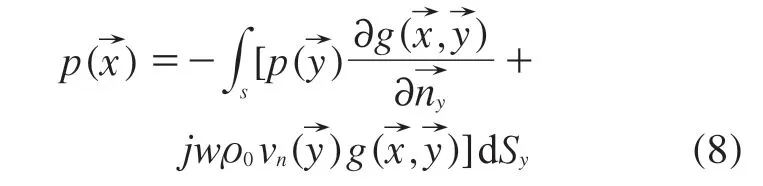
式中，ρ0为空气密度，g（x，y）为格林函数的偏导数。计算求得结构表面S上节点的声压p(和振动速度v n()，即可求得空间域Ve内任意空间点处的声压值p(x)。

2 轮胎振动辐射噪声数值计算

首先，采用Abaqus/Explicit方法进行轮胎显式滚动分析，提取轮胎与路面的激励力；然后，运用模态声学传递向量的方法预测轮胎振动辐射噪声；最后结合轮胎外轮廓各部件的声学贡献度，分析峰值频率下轮胎各部件的贡献度。

2.1 轮胎有限元分析模型

以295/80R22.5载重子午线轮胎为研究对象，利用Abaqus软件，采用文献[3]中的方法建立轮胎有限元模型，如图1所示。橡胶部分采用CGAX3和CGAX4R单元进行模拟，钢丝帘线采用SFMGAX1和REBAR单元进行模拟。橡胶的本构模型采用Neo-Hooke模型，材料参数采用单轴拉伸试验数据进行曲线拟合得到。路面定义为解析刚体，路面与轮胎之间的摩擦采用库伦摩擦定律描述。

图1 轮胎三维有限元模型

有限元分析过程采用标准负荷3 550 kg和标准气压900 kPa。在Abaqus软件中完成对轮胎的装配、充气、加载和自由滚动分析。滚动分析时轮胎与路面的摩擦因数取0.7，滚动速度为70 km·h-1。

2.2 轮胎模态试验及有限元分析

模态分析是一种以试验为基础的结构动态特性分析方法。为验证轮胎有限元模型建立的正确性，采用法国OROS公司的动态试验设备进行轮胎的模态试验。试验过程中，轮胎处于自由悬置状态，轮胎表面设置81个均匀分布的测点。

试验采用锤击法激励，利用加速度传感器测量响应信号。将激励和响应信号放大后输入动态分析仪，分析处理得到0～200 Hz范围内的传递函数。试验得到轮胎自由悬置状态下前6阶固有频率和振型，如图2所示。

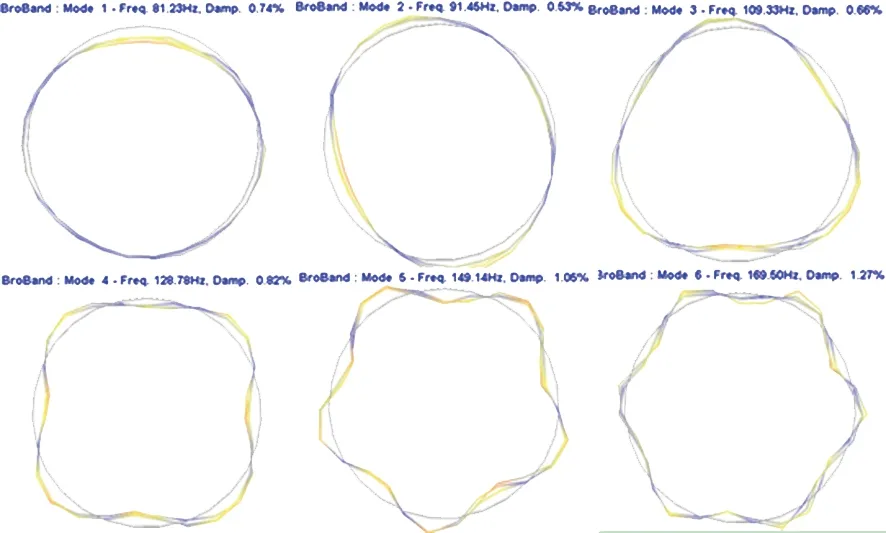
图2 轮胎前6阶模态振型

轮胎自由模态分析采用Block Lanczos法，求出其计算模态，并与试验模态进行比较。有限元分析和试验得到的固有频率对比见表1。由表1可见，应用Abaqus建立的轮胎有限元模型能很好地计算轮胎的各阶模态。计算模态频率普遍比试验模态偏低，其原因主要是建立轮胎有限元分析模型时对其结构进行了简化，且忽略了轮辋，使计算结果产生一定的误差。该误差满足分析要求，验证表明该有限元模型是正确的。

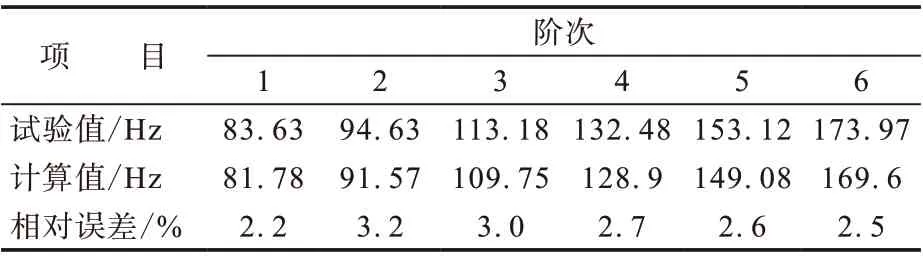
表1 轮胎试验模态与仿真模态对比

2.3 轮胎振动辐射噪声数值分析

2.3.1 轮胎声学边界元模型建立

将自由滚动状态下的轮胎有限元模型导入Hypermesh中提取面网格，为了避免声能量泄露，在轮辋处设置圆形区域，将声学边界元模型封闭起来，轮胎声学边界元模型如图3所示。

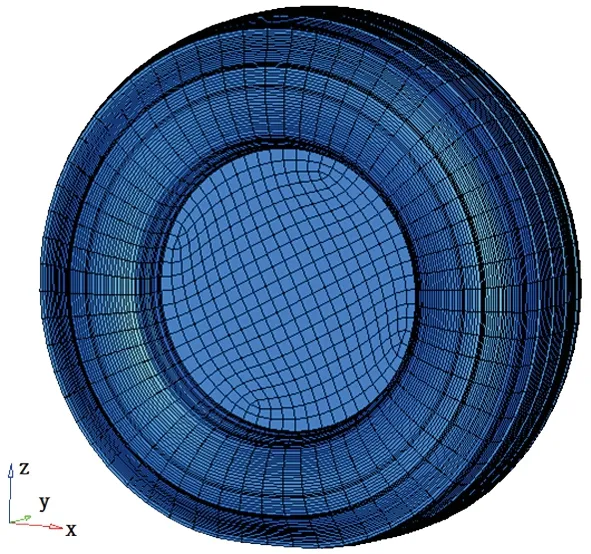
图3 轮胎声学边界元模型

所建立的边界元模型共16 440个单元，16 434个节点。该模型的节点与滚动分析的有限元模型相应的节点号和节点坐标完全一致。从而保证了有限元振动信号传递到边界元网格的准确性。

考虑到轮胎的对称性，根据GB/T 3767—1999《声学 声压法测定噪声源声功率级 反射面上方近似自由场的工程法》，在其周围建立半径为1 m的半圆罩型模型，该模型定义了19个声学观测点。分析时定义路面为刚性反射面。轮胎振动噪声声压值通过声压叠加的方法计算场点网格19个观测点的A计权声压均值。通过计算分析得知，场点网格上的19个声学测点的声压频响函数曲线变化趋势一致，只是声压值的大小不同。不失一般性，本工作以观测场点网格上第15个场点为声学观测点，分析轮胎外轮廓结构各部件的声学贡献度。声学分析模型与声学观测点如图4所示。

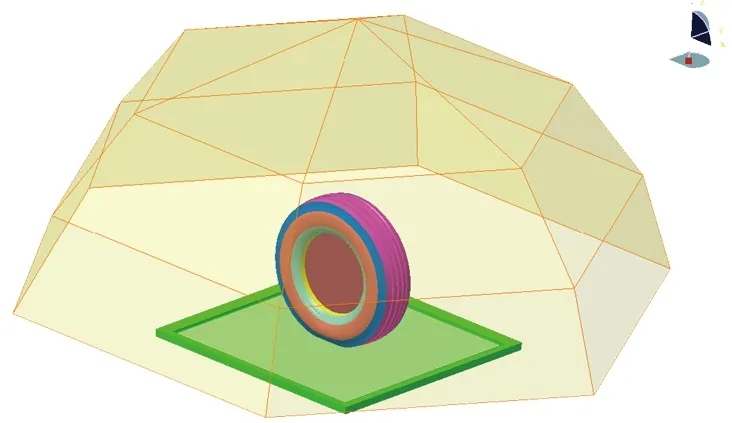
图4 声学分析模型与声学观测点

2.3.2 轮胎振动辐射噪声数值分析

提取轮胎在路面稳态滚动时所受的径向激励力，如图5所示。采用傅里叶变换方法将其转化为声学计算时频域边界条件，如图6所示。以此力作为激励力施加在轮胎与路面接触的中心点，导入轮胎模态分析结果，求其模态参与因子。声压求解过程中，通过数据转移将轮胎表面节点信息映射到声学网格上，运用模态声学传递向量技术计算原始设计20～400 Hz轮胎振动辐射噪声A计权声压值为76.88 dB。

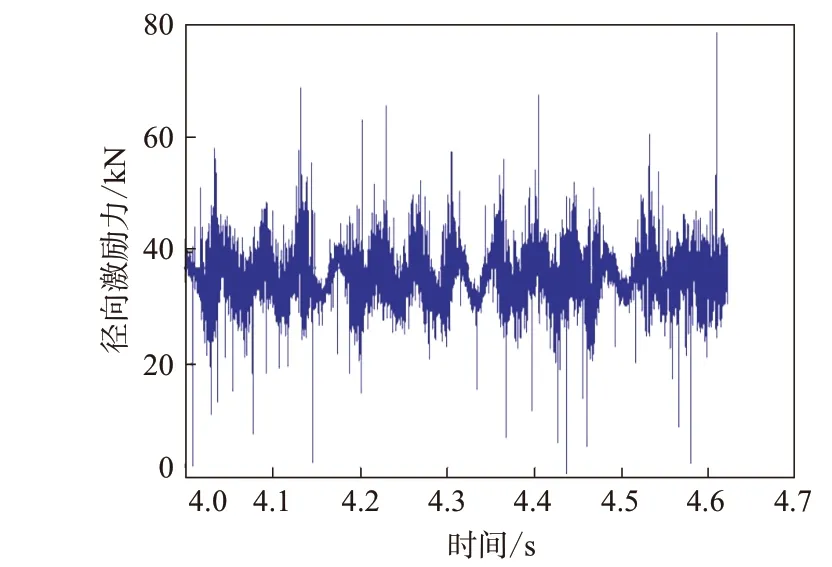
图5 轮胎径向激励时域图

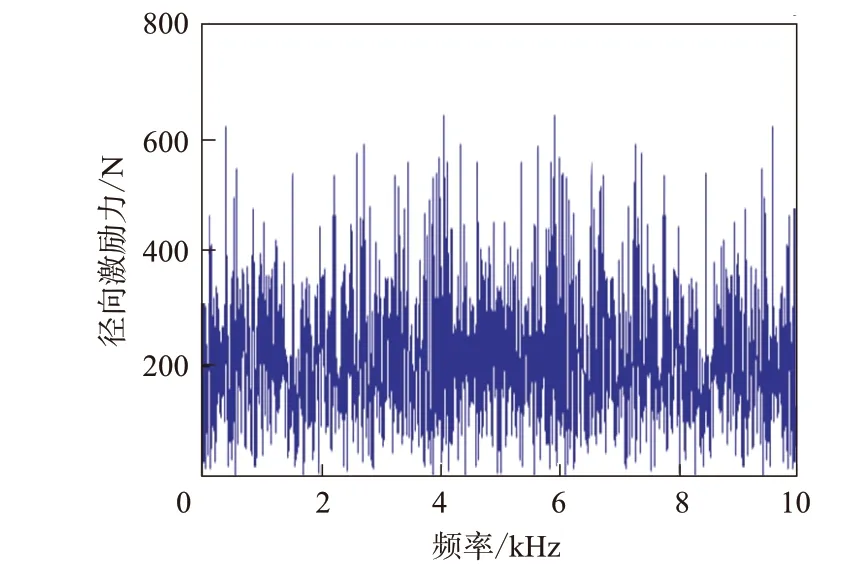
图6 频域内的激励力

3 轮胎外轮廓声学贡献度分析

3.1 声学贡献度分析方法

声场内某点声压可看作由边界面S各有限单元发出声波在该点贡献的叠加，为量化每个部件对场内噪声的贡献程度，引入结构声学贡献度概念。单元对某场点的声学贡献度Ce是该单元振动生成声压p在该点总声压矢量上的投影，表达式为

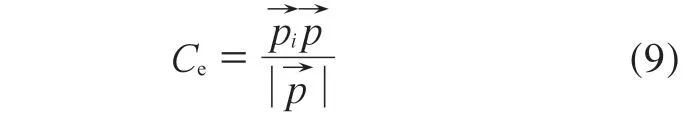
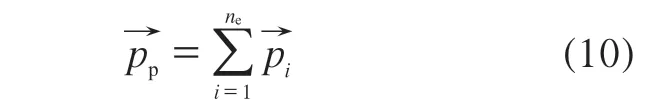
式中，ne是组成该部件的单元数。

同理，部件声学贡献度（Cp）为

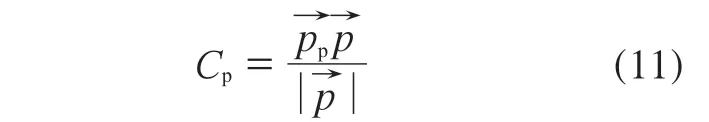
从声学贡献度的定义可知，存在正负声学贡献度。正贡献度表明总声压随该面板振动幅值的增大而升高，结构改变时减少板件振动可降低；负贡献度表明总声压随该面板振动幅值的增大而降低，结构改变时利用其振动来衰减。

由式（9）可知，当某个部件的声学贡献相位与总的声学贡献相位一致，且该部件的声压贡献幅值最大，称为主最大声学正贡献部件，减少其振动可以降低总声压。当某个部件的声学贡献相位与总的声学贡献相位相反且该部件的声压贡献最大，称为主最大负贡献部件，可以利用其振动降低总声压。因此，在进行结构改变前，须进行声学贡献分析以确定对噪声影响最大的部件，进而改变对噪声贡献最大的部件区域，以达到降低噪声的目的[7]。

3.2 轮胎外轮廓声学贡献度分析

为了准确分析轮胎外轮廓各部件的声学贡献度，将外轮廓分成6个部分，如图7所示。

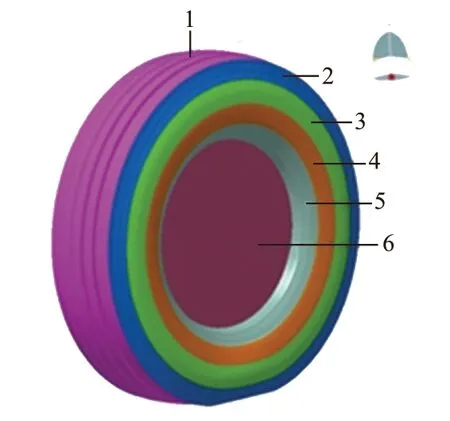
图7 轮胎外轮廓各部件模型

参照轮胎振动辐射噪声数值分析方法，运用模态声学传递向量技术计算声学场点网格第8号观测点的A计权声压频响函数，结果如图8所示。

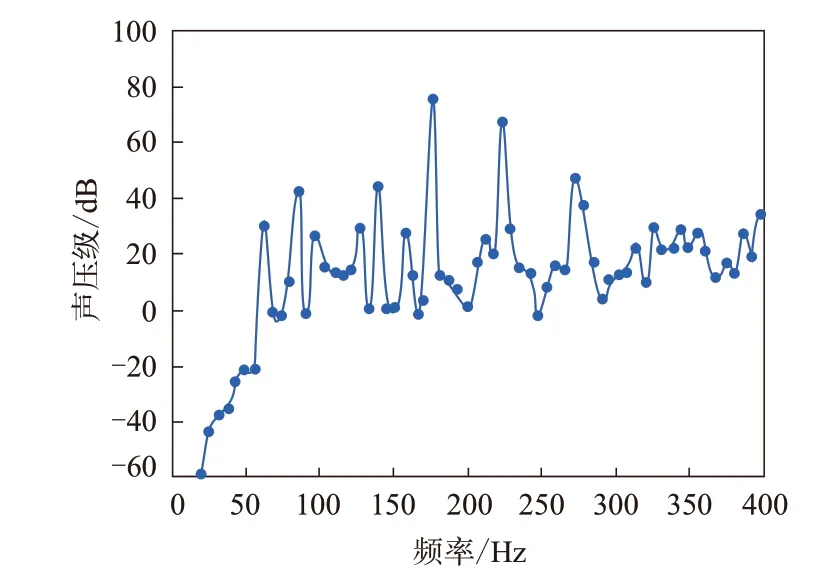
图8 场点声压频响函数曲线

从图8可以看出，在频率为86，140，176，224和278 Hz时，声压级出现较为明显的峰值。因此，要降低轮胎的振动辐射噪声，应降低对应频率的声压贡献度较大的轮胎外轮廓部件的噪声。

轮胎外轮廓各部件在上述5处峰值频率下的声压幅值和相位贡献度见表2。由表2可知：在峰值声压频率176 Hz处，胎面和上胎侧区域为主要正贡献部件，胎面声压幅值贡献最大；胎侧中部和下部区域声压贡献幅值也较大，但是其相位与总相位相反，为负贡献部件；而轮辋区域由于刚性较大，振动相对较小，其对总声压幅值和相位贡献均为负。综合分析，对轮胎声压峰值贡献最大的轮胎结构部件为胎面和上胎侧区域，且在不同频段各部件的贡献度不同，胎面和上胎侧的振动是轮胎振动噪声的主要来源。

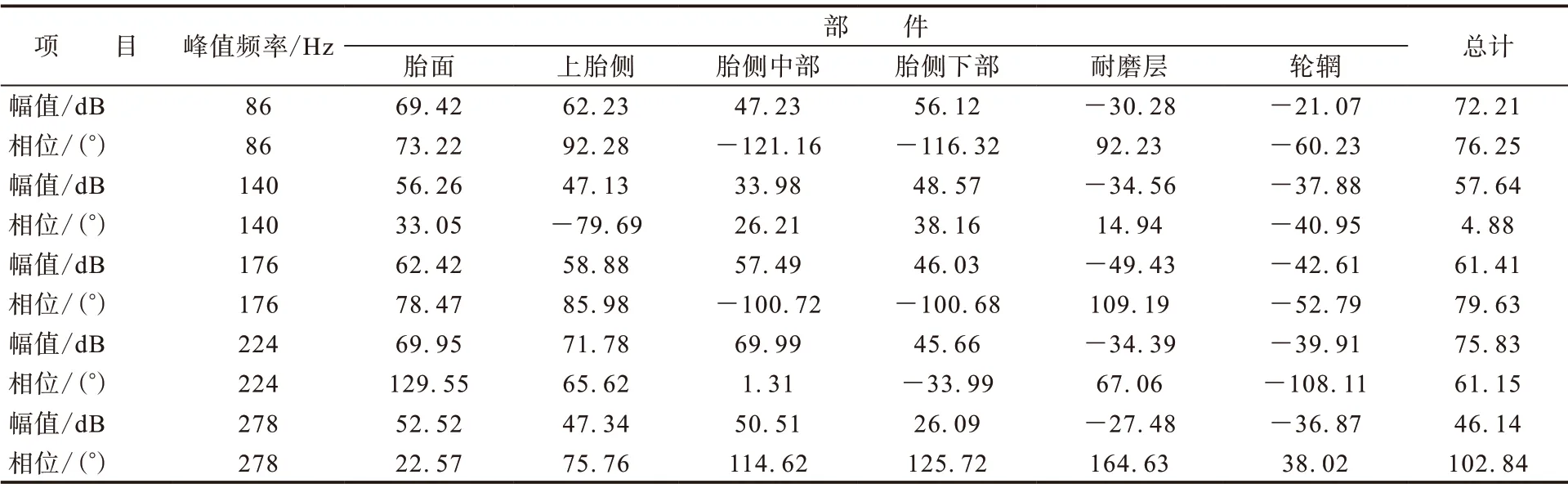
表2 轮胎外轮廓各部件声学贡献度

4 轮胎水平轴位置和加强层高度对轮胎噪声的影响分析

轮胎水平轴位置和加强层高度对胎体轮廓存在显著影响，改变水平轴位置会改变轮胎内部结构的应力应变特性；改变加强层高度会改变胎圈宽度对胎体轮廓的受力影响[10]。

现行设计、改变水平轴位置（增大5 mm）和加强层高度（增大2 mm）的轮胎声压频谱对比如图9所示。由图9可知，轮胎现行设计的声压峰值频率为176 Hz，修改水平轴位置和加强层高度的声压峰值频率分别为116和224 Hz。

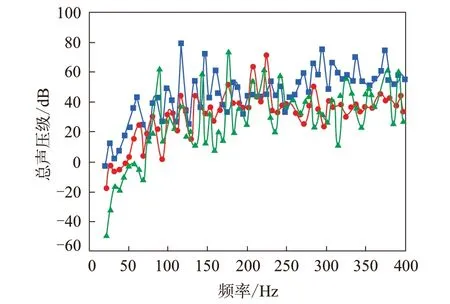
图9 各方案声压级频谱对比

不同方案各峰值频率的声压级对比见表3，外轮廓各部件贡献度分析结果见表4。从表4可以看出：在现行设计轮胎最大声压峰值所对应的频率176 Hz处，改变水平轴位置和加强层高度对轮胎外轮廓表面声学贡献度影响较大；改变水平轴位置后，耐磨层相位贡献变为负；改变加强层高度后，胎面和上胎侧依然为声学正贡献部件，而胎侧中部和胎侧下部声学贡献幅值变为负。

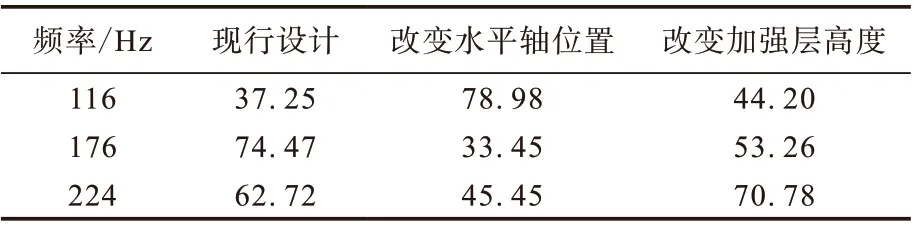
表3 不同方案各峰值频率下对应的声压级对比 dB

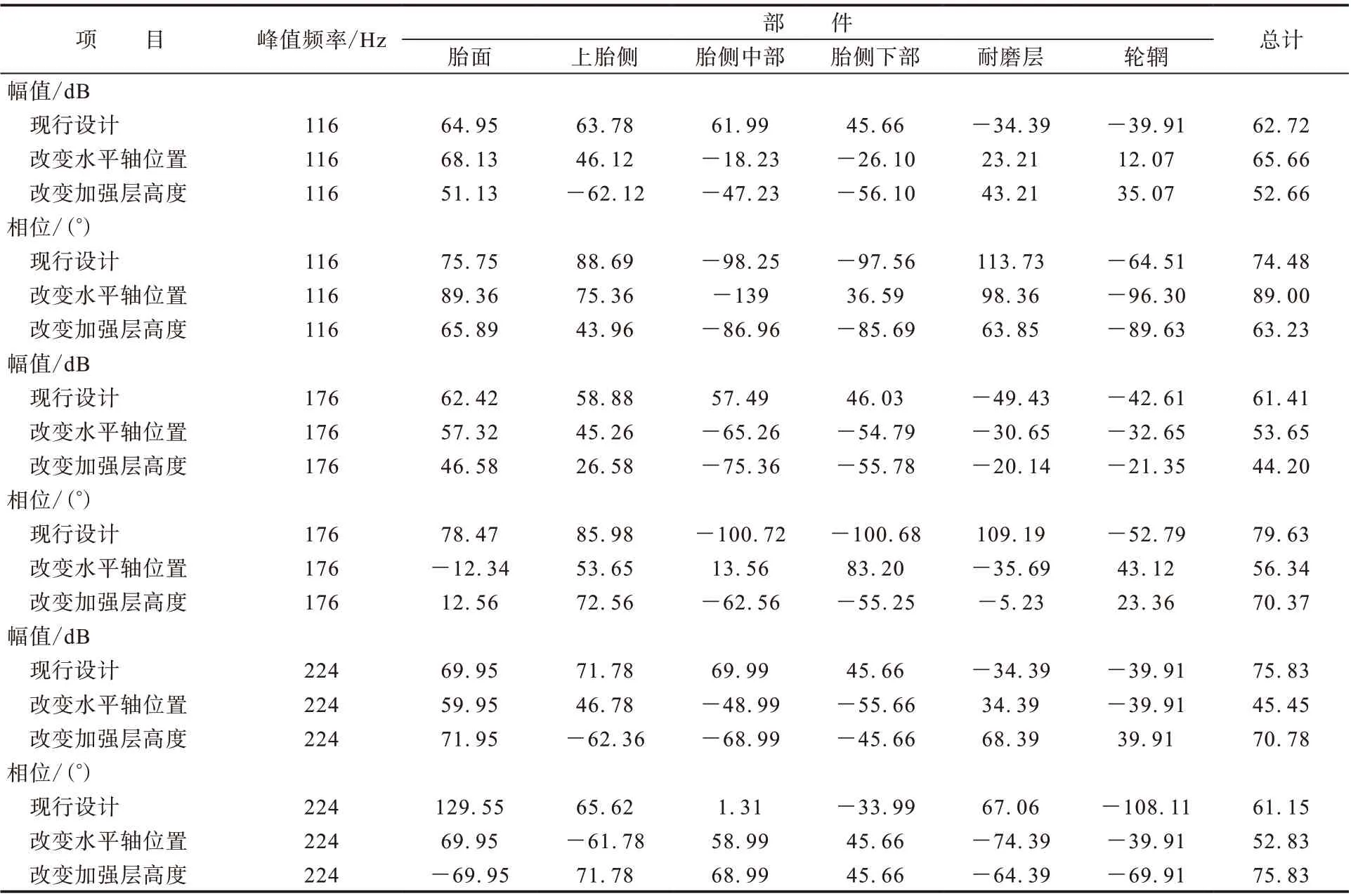
表4 不同方案轮胎外轮廓部件声学贡献度

在改变水平轴位置后最大声压峰值所对应的频率116 Hz处，其声学正贡献部件依然为胎面、上胎侧和耐磨层，但胎面区域振动更为强烈，这是由于水平轴上移后，胎面区域受力变大所致；修改加强层高度后，上胎侧区域的声学贡献度明显减小，下胎侧区域的声学贡献度增大。改变加强层高度后最大声压峰值所对应的频率224 Hz处，胎面和耐磨层区域的声学贡献度增大，而胎侧区域声学贡献度减小，且上胎侧成为声学负贡献部件。

综合分析，改变轮胎水平轴位置和加强层高度会影响声压峰值所对应的频率处轮胎外表面各结构部件对声压的贡献度，对于同一型号的轮胎，采用标定宽度较小的轮辋时，可采取提高水平轴位置的方法抑制胎圈部位的振动；增大加强层高度可抑制胎侧区域振动，进而改变轮胎声学特性。

5 结论

（1）改变轮胎水平轴位置和加强层高度会改变声压峰值处轮胎各结构部件对声压的贡献量，对轮胎声学特性产生明显影响。

（2）降低轮胎外轮廓声学正贡献部件的声压幅值，或增加负贡献部件的数量，可以达到降低轮胎振动辐射噪声的目的。

（3）改变轮胎结构设计参数能够达到改变轮胎外轮廓结构部件的声学贡献度特性的目的，为低噪声轮胎结构设计提供了指导。