高速永磁同步电动机用电磁-气体箔片混合轴承设计
2016-07-26樊登柱徐凡
樊登柱,徐凡
(1.南通职业大学 汽车与交通工程学院,江苏 南通 226007;2.西安交通大学 机械工程学院,西安 710049)
与传统的电励磁电动机相比,稀土永磁同步电动机具有多重优点[1], 因此广泛应用于航空航天、汽车船舶、医疗器械、发电系统等领域。由于高速电动机自身特点[2],导致其轴承使用寿命过短,强度和性能很难满足要求,并且定子温度较高,影响材料性能,因此,选用合理的支承方式和材料至关重要。目前研究的轴承类型有含油轴承、空气轴承及磁悬浮轴承,另外,特殊设计的滚动轴承也用于航空航天、高精密主轴等领域。电磁-气体箔片混合轴承是将电磁轴承和气体箔片轴承组合使用的支承方式,可以达到简化结构,提高承载力、动态刚度以及系统阻尼和稳定裕度,减小轴承发热的目的[3-4]。
研制更高转速下的永磁同步电动机结构及其支承方式,对于超高速超精密加工机床、飞轮、涡轮膨胀机、离心压缩机、磁悬浮航空发动机以及微型燃气轮机等领域有着重要的理论指导意义和应用价值。现通过推导理论公式,设计一种电磁-气体箔片混合轴承,并通过有限元方法对轴承进行模态分析,验证在工作转速范围内,轴承-转子系统的安全性。
1 电动机-混合轴承系统性能要求及结构设计
1.1 系统性能要求
提出一种高速永磁同步电动机用嵌套式电磁-弹性气体箔片混合轴承。该系统中电动机的设计目标为:功率60 kW,转速45 000 r/min。轴承设计和性能要求为:内径46 mm,环境温度150 ℃,允许最高环境温度为200 ℃,工作时最小轴向力为150 N,最大轴向力1 500 N,套圈材料应具备一定的可靠寿命。
1.2 电动机转子及混合轴承整体设计方案
基于电磁-气体箔片轴承支承的电动机结构如图1所示,电动机以三段式布置,两端采用电磁-气体箔片混合轴承支承,并在一端的轴承与定子之间采用推力滑动轴承作轴向定位,转子选择中空结构,通以高压冷却气体。电磁-气体箔片轴承可以承受径向载荷,也可以支承转子;推力轴承可以承受轴向载荷,保证转子的正常运作[5]。电动机转子结构如图2所示。

图1 高速电动机整体结构
1.3 电磁-气体箔片混合轴承结构设计
1.3.1 电磁轴承结构设计
电磁轴承普遍以电磁铁设计理论为基础,采用磁路法对选定的指标进行结构参数设计。径向电磁轴承由定子与转子组成,线圈绕在磁极上。定子采用8极周向结构,这种结构易于制造,且精度相对较高,同时,考虑减小涡流损耗和磁滞,避免极间耦合,磁极按NNSSNNSS沿周向排列,如图3所示。
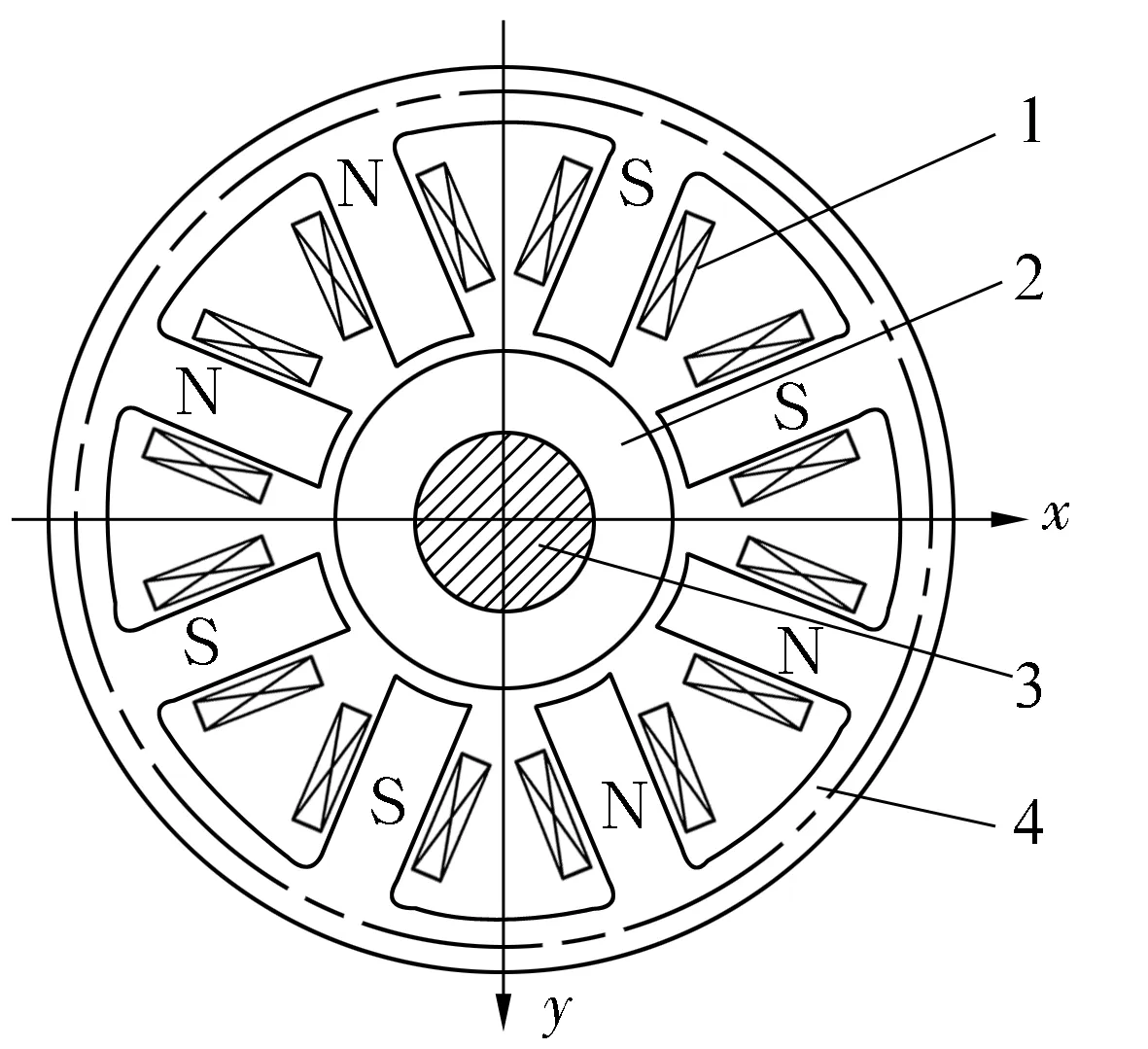
1—线圈;2—轴颈;3—轴;4—定子
电磁轴承材料常用硅钢片、碳钢、合金钢、永磁铁等。设计时为获得良好的特性、提高电磁轴承的承载能力、减小铁芯内部涡流,电磁轴承的定子和转子需要具有较高的导磁性能、材料饱和磁感应强度、相对磁导率以及较低的铁损率,结合实际加工等因素,选择硅钢片作为轴承材料。
系统静态工作点取在图4所示的材料磁化曲线线性段中点B0,以保证电磁轴承在最大输出时仍不至于出现磁饱和现象,图中B为磁感应强度,Bmax为饱合磁感应强度最大点,H为磁场强度。

图4 材料磁化曲线
定子线圈槽形状如图5所示。梯形槽和圆形槽能保证铁芯齿部磁通密度均匀,没有过饱和点,有利于降低激磁电流与铁损,而圆形槽的外径相对梯形槽大,因此,为使结构紧凑,选择梯形槽作为电磁轴承的线圈槽型。
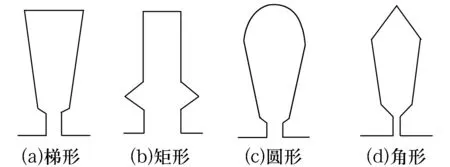
图5 径向电磁轴承的槽型


图6 径向电磁轴承示意图Fig.6 Diagram of radial electromagnetic bearing
1.3.2 气体箔片轴承结构设计
弹性气体箔片轴承的主要结构分为顶层箔片和底层箔片,其结构如图7所示,图中:O为轴承的几何中心;α0为底层箔片张角;Rh为顶层箔片半径。底层箔片为拱形波浪式结构,既可以减少箔片在运转过程中与转子的接触面积,也可以增大气体进入轴承的流通量,底层箔片的另一端通过楔子锁入轴承座中;顶层箔片为平箔,起保护底层箔片的作用。考虑到转子高速运转过程中产生的温度较高,两者均选用耐高温镍基合金制成。
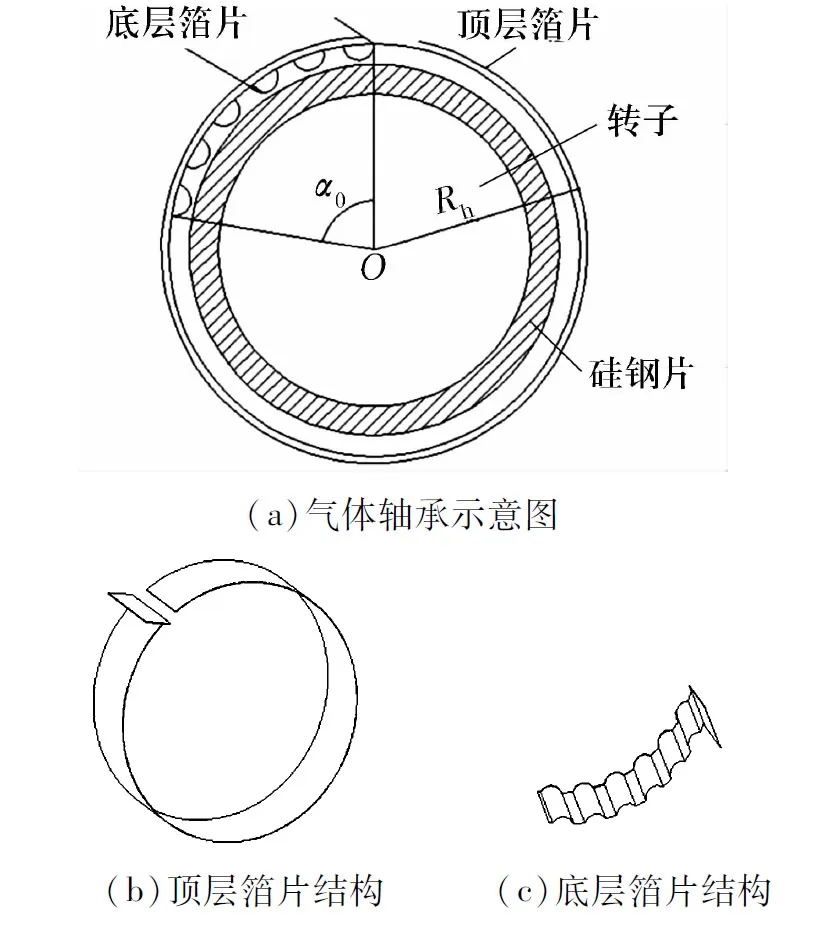
图7 弹性气体箔片轴承结构Fig.7 Structure of elasticity gas foil bearing
设计时,先以估算得到各结构参数,后期再进行修正。底层箔片张角为
(1)
式中:nf为顶层箔片箔的数目。
1.3.3 混合轴承结构设计
电磁轴承和气体箔片轴承设计加工完成后,将气体箔片轴承安装入电磁轴承座内部的空隙中,安装后结构如图8所示。电磁轴承内壁设有磁极,外部径向上设有电磁轴承底座,轴向上设有左右端盖,端盖通过螺钉固定在电磁轴承底座上。底层气体箔片内壁涂上PS304粉末,可以减小轴颈与底层箔片的摩擦,同时保护底层箔片与轴颈[7]。

1—轴承座; 2—电磁轴承硅钢片组件; 3—线圈; 4—弹性箔固定垫片; 5—轴承座组件; 6—底层箔片; 7—顶层弹性箔片
2 混合轴承的承载力计算及结构优化
2.1 承载力公式推导
在计算径向电磁轴承近似承载力时,假设磁通除气隙外无漏磁、磁铁磁导率比空气磁导率大得多,并且磁力线始终几乎垂直于气隙方向。
电磁轴承磁极为NSSN配置,采用差动控制。电磁轴承上下两磁极对同时激励时磁路的示意图如图9所示,差动模式控制示意图如图10所示,图中I0为偏磁电流;i为控制电流;F为电磁合力;s0为定转子初始距离;y为差动偏移量。

图9 电磁轴承磁路示意图

图10 电磁轴承差动模式控制示意图
对于磁极均布的径向轴承,当转子发生偏心时,经过推导,若向下偏移x(见图6a,向下为x轴正方向),则上面一对磁极气隙中的磁感应强度为
(2)
式中:μ0为真空磁导率,取4π×10-7N/A2;N为线圈匝数,取20;I为线圈中的偏磁电流值。
此时,上面一对磁极在x方向上的磁悬浮合力为
(3)
A0=KdtLr,
式中:Kd为叠装系数,取0.94~0.98。为便于计算,计算图10中转子处于几何中心的电磁力与磁感应强度时,令x=0。
差动控制模式下,当转子在x方向向下偏移时,上、下磁极对中产生的电磁合力Fm为
(4)
实际上,若电磁合力方向与重力方向一致,则静平衡时的电磁合力F0与转子自身重力相平衡。联立(3)式、(4)式可推导出
(5)
式中:ix0为静态反馈电流;m为轴承分担的转子质量;g为重力加速度。
因此,上、下电磁铁中的实际偏磁电流依次为I0+ix0,I0-ix0,则(4)式可写为
。 (6)
转子处于几何中心(x=0)且控制电流i=I0时,磁极对中气隙磁感应强度为Bmax,径向轴承的最大名义磁悬浮力为
(7)
与此同时,对于气体箔片轴承的承载力分析仍然处于探索阶段。最常用的计算公式是在牛顿第一定律的基础上并结合试验数据综合分析,得到气体箔片轴承承载力的经验估算公式
W=β(Bl×D)(D×n),
(8)
式中:W为稳态时最大载荷,N;β为轴承载荷系数;Bl为轴承宽度,mm;D为轴颈直径,mm;n为转速,r/min。
相关试验研究结果表明,在30 000 r/min的转速下,电磁轴承只承担了20%的载荷,气体轴承承担了80%的载荷[8]。由此可见,气体轴承嵌入电磁轴承内,电磁轴承最大承载力不变时,混合轴承可显著提高磁轴承的承载力。
2.2 混合轴承结构优化
根据电磁轴承承载力特点,对混合轴承进行结构优化以提高承载性能,优化后的混合轴承端盖结构如图11所示。在靠近磁极根部附近,左右端盖设有能够通过支口配合重合的突台,端盖内壁上沿圆周方向均匀布置有不规则梯形槽,槽内安装有顶层弹性箔片和底层弹性箔片,箔片通过电磁轴承左右端盖施加的挡圈固定。相比于优化前左右端盖的光轴结构,优化后由于配合支口和不规则梯形槽结构,使混合轴承的承载性能得以提高。电磁轴承线圈通电后在极靴与转子轴颈之间形成了电磁场,极靴对转子轴颈产生吸引力,当转速上升到一定值时,在顶层弹性箔片与转子之间形成一定的承载力后将转子浮起。

图11 电磁-气体箔片混合轴承左右端盖结构图
优化后的电磁-气体箔片混合轴承有以下优点:1)采用镶嵌式结构,集成度高;2)动态刚度和承载力提高;3)阻尼和稳定性高,弹性气体箔片轴承可提供较高的结构阻尼。因此,混合轴承不但可以提高系统的阻尼和稳定性,还可以简化电磁轴承的控制系统。
3 混合轴承转子系统仿真分析
3.1 动力学有限元分析方法
利用有限元法分析高速永磁同步电动机转子系统的动力学特性是一种行之有效的途径[9],通过分析转子系统的动力学特性,包括临界转速和模态阵型的计算,可以保证永磁同步电动机在高速运行时的稳定性和可靠性[10]。
进行转子动力学分析时,常采用基于Timoshenko梁-轴的有限元分析法,因为在转子高速运动时,陀螺效应对其涡轮频率有较大影响,而且转轴的转动惯量和剪切变形也会对转轴的动力特性产生影响。
把转子划分成轴段、圆盘、轴承等一系列的基本单元,然后根据能量、受力等关系建立相关运动方程,最后求解所需参数。
3.2 有限元仿真
与永磁体类似,硅钢片是叠加而成的,对转子的整体刚度影响较小,且质量较大,在高速旋转时会产生较大的陀螺效应,故考虑其质量矩阵与惯量矩阵融入到相应的轴段矩阵中;传感器检测环长度较短,对转子的整体刚度影响也较小,因此也仅考虑其质量矩阵与惯量矩阵融入到相应的轴段矩阵中;推力盘简化为规则圆盘结构,与保护套结构类似处理,将其质量矩阵、惯量矩阵与阻尼矩阵融入到相应的轴段矩阵中。
转子轴段单元网格划分如图12所示。由于电磁-气体箔片混合轴承的动力学参数求解相对困难,因此暂取混合轴承的支承刚度为106N/m,同时忽略支承阻尼,由于推力轴承对转子的影响也较弱,因此忽略其影响。

图12 转子轴段单元网格划分
在额定工作转速45 000 r/min下,计算得到转子的固有频率见表1,相应的模态振型如图13所示。由图可知,在一阶弯曲固有频率下,转子表现出了典型的一阶弯曲模态振型。由表1可知,转子的一阶弯曲固有频率为1 405,1 566 Hz,分别是额定工作频率750 Hz的1.88,2.08倍,因此,轴承转子系统在设计转速范围内可以在刚性状态下安全工作,动力学性能满足要求。
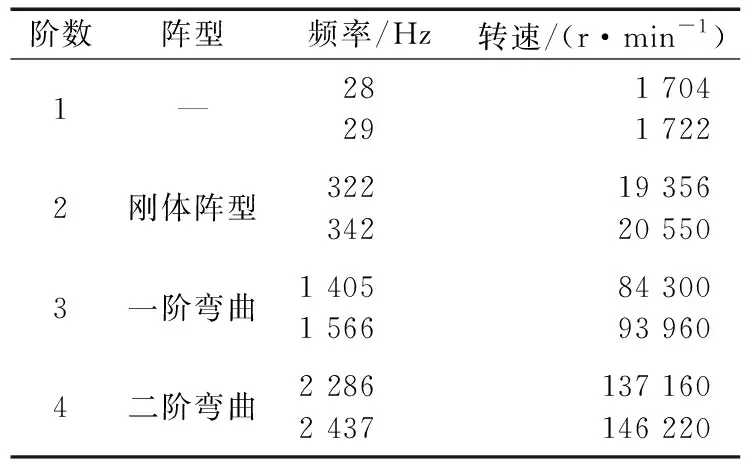
表1 转子的固有频率和临界转速

(a)频率为1 405 Hz
4 结束语
设计的电磁-弹性箔片混合轴承不仅承载力大、可控制性强,而且嵌套式结构可以从整体上提高轴承的支承能力,还起到了简化结构、缩短转子轴向长度、减轻质量的作用。通过轴承-转子动力学仿真证明,在设计转速范围内混合轴承-转子系统能够安全工作,提出的设计、分析方法在高速电动机用轴承领域具有参考和实用价值。
