不同能量载荷下球罐壁面响应的数值研究*

魏荣宽　关文玲　高彤　尹鑫伟

(天津理工大学环境科学与安全工程学院　天津 300384)



不同能量载荷下球罐壁面响应的数值研究*

魏荣宽关文玲高彤尹鑫伟

(天津理工大学环境科学与安全工程学院天津 300384)

摘要容器爆炸碎片是造成化工企业多米诺效应的重要原因之一，研究不同能量载荷下容器壁面响应规律有助于分析事故原因及碎片形成机理。本研究以化工企业常用的储存容器球罐为研究对象，利用LS-DYNA软件对不同能量载荷下球罐壁面响应过程进行数值分析，研究表明球罐壁面在不同的爆炸载荷下出现不同的响应结果，因此可以根据容器响应后果来判定爆炸载荷的临界值；根据能量守恒可以对发生破裂的球形容器形成碎片过程中不同时刻的动能进行追踪，该结果可以为判定碎片发生多米诺效应的可能性提供参考。

关键词壁面响应球罐能量载荷动能

0引言

球罐是化工企业常用的一种储存容器，常被用来贮存液态或气态物料。球罐中常装有高压气体或者过热液体，当超压、机械失效或者受外力作用时球罐可能发生失效产生碎片，碎片是造成化工企业多米诺效应的重要原因之一。因此研究不同能量载荷下球罐壁面响应规律对于分析事故原因以及碎片形成机理具有重要的理论意义。在化工企业球罐发生爆炸时，主要的原因是化学反应失控或存储过程中过量充装等原因引起，能量的载体一般是液态或者气态物质，在本研究中将事故球罐中的液态或者气态物质所具有的能量用凝聚态炸药来表示，LS-DYNA软件对于分析凝聚态炸药爆炸过程中的大变形动力响应问题与实验结果较为相符，因此本研究选用LS-DYNA软件对不同能量载荷下球罐壁面响应过程进行数值模拟和分析。

1网格的划分及破坏准则的确定

1.1网格的划分

Lagrange、Euler、ALE是数值模拟中处理连续体的广泛应用的3种方法。

Lagrange方法多用于固体结构的应力应变分析；Euler方法以空间坐标为基础，多用于流体的分析中。ALE方法最初出现于数值模拟流体动力学问题的有限差分方法中。这种方法兼具Lagrange方法和Euler方法二者的特长，即首先在结构边界运动的处理上引进了Lagrange方法的特点，因此能够有效的跟踪物质结构边界的运动；其次在内部网格的划分上，它吸收了Euler的长处，即使内部网格单元独立于物质实体而存在，但又不完全和Euler网格相同，网格可以根据定义的参数在求解过程中适当调整位置，使得网格不致出现严重的畸变。因此，利用ALE算法的网格可以随物质一起运动，也可以被固定在空间不动，甚至可以在一个方向上随物质运动，而在另外一个方向上固定不动，这种方法在分析大变形问题时是非常有利的。

本文选用ALE方法，将炸药定义成流体以避免爆炸过程中网格的过份畸变而造成对计算结果的不利影响。

1.2容器破坏准则的选取

球罐的金属材料在外部载荷的作用下，发生变形和破裂的过程分为弹性变形、弹塑性变形及断裂3个阶段，在受到外部载荷时，材料某一点上的3个主应力σ1、σ2、σ3可能都不为零，从而出现不同的主应力组合。因为材料存在着脆性断裂和塑性屈服两种破坏形式，相应的强度破坏理论也分为两类，其中最大拉应力理论和最大伸长线应变理论解释脆性断裂；最大切应力理论和最大形状改变比能理论解释塑性屈服，因为工业容器的材质以钢材为主，因此在受到外力冲击时会产生塑性屈服。塑性屈服准则为最大切应力准则和最大形状改变比能准则。其中最大切应力准则能够很好的描述低强化韧性材料(例如退火钢)的屈服状态。最大形状改变比能准则能够很好的描述铜、镍、铝等大量工程韧性材料的屈服状态[1]。化工容器所采用的材质一般为合金钢，因此本文材料的本构模型依照该准则建立。

2计算实例

2.1有限元模型的确定

本研究选用的球罐容器内径R=0.6 m, 容器壁厚18 mm，根据Vons Mises等向强化准则，材料取理想弹塑性模型，计算模型采用Solid164实体单元进行网格划分，采用单位制为厘米-克-微妙(cm-g-μs)，网格尺寸0.18 cm，共约188 170个节点，计算时间80 μs，网格模型见图1，在模拟过程中球罐采用1/8模型，以共用节点的方式连接起来。

2.2材料的本构模型

2.2.1炸药的有限元模拟

炸药单元选用“Programmed+beta burn”技术模拟炸药的爆轰过程，通过Euler网格建模，采用ALE算法，材料模型选用“Explosive Burn”材料模型。炸药化学能量的释放由燃烧因子控制，每个炸药单元的点火时间根据该单元中心至起爆点的距离和爆速确定[2]。炸药选用JWL状态方程模拟炸药爆轰过程中压力和比容的关系：

图1　球形容器网格模型

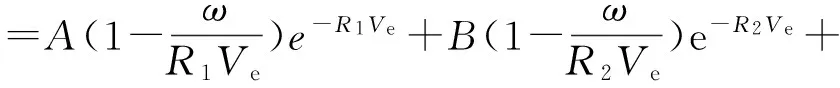
(1)

式中，ETNT为初始比内能，Pe为压力，Ve是相对体积，A、B、R1、R2、ω为材料常数。

本研究采用TNT炸药，其相关参数见表1。

表1　炸药的状态方程参数[1]

2.2.2钢材料的本构模型

钢容器本身采用Lagrangian算法，和炸药间采用流固耦合算法，采用16MnR钢，其相关参数见表2。

表2　钢材料的弹塑性模型参数

在球罐受到爆炸载荷作用时，球罐内部爆炸可能产生冲击波，冲击波在爆炸产物中传播、绕射和反射，空气、爆炸产物和容器结构的碰撞与运动，容器内部结构变形等效应相互影响，形成了一个非常复杂的作用过程。因为球罐壁的变形对内部流场的影响比较小，因此在研究爆炸流体对球罐器壁的影响时不考虑器壁对流体的作用，这样可以使得数值求解载荷问题时的边界条件处理相对简单，因此本研究使用流固耦合算法来处理爆炸流体与器壁的作用，将炸药、ALE空间两种流体网格分别定义多物质组，并与固体网格间定义流固耦合。上面3种介质中，炸药、ALE空间采用Euler算法，钢采用Lagrangian算法。计算模型采用Solid164实体单元进行网格划分，炸药、ALE空间采用多物Euler描述法；钢采用Lagrangian描述法。初始条件为所有节点的初始位移、速度和加速度均为零。

2.3模拟结果和分析

2.3.1不同能量加载下球罐的变形情况分析

在计算时间80 μs内，不同的爆炸载荷作用下，球罐器壁出现不同的响应。研究其1/8模型，在爆炸能量为1 GJ时，容器仅发生小变形，见图2(a)；爆炸能量为16 GJ时，1/8模型开始出现裂纹，见图2(b)；爆炸能量为27 GJ时，破裂为碎片，见图2(c)。因此在事故调查中可以根据事故现场球罐的变形情况反推球罐壁面所加载的的最小能量载荷即其不同破裂程度时载荷的临界值。

(a)E=1 GJ小变形　　　　(b)E=16 GJ刚开裂

(c)E=27 GJ产生碎片

2.3.2不同能量加载下罐壁所具有的能量分析

对1/8球罐小变形以及形成碎片时的器壁总动

能进行了分析计算，结果见图3、图4，在零时刻，容器器壁的动能为0。动能分为两个部分，一部分是薄弱区(或连接区)的动能，一部分是器壁动能。对比这两部分的动能，在小变形情况下(图3)，连接部位具有一定的能量，当容器破裂后(图4)，连接处开裂，动能为零。从图中还可以看出，形成碎片的容器壳体动能要远高于小变形时，这和实际情况是相符的。因此对于在爆炸过程中形成的碎片总动能的计算有助于推断该球罐爆炸时产生碎片可能引发多米诺效应的范围，从而为企业在规划和设计阶段的平面布置提供依据。

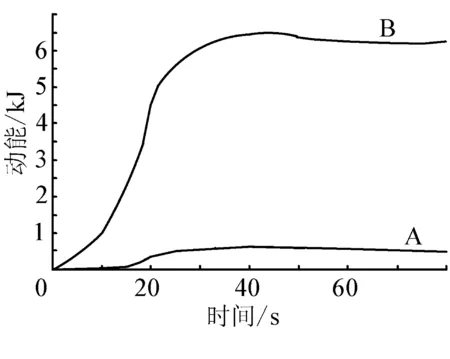
A 表示罐壁连接处、B 表示除连接处外罐壁的总动能

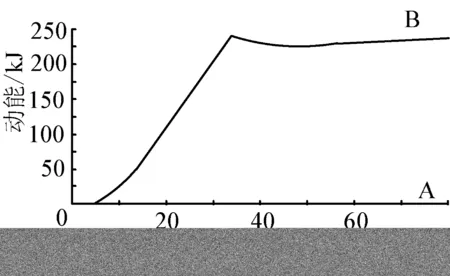
A 表示罐壁连接处、B 表示除连接处外罐壁的总动能

2.3.3不同能量载荷下罐壁的应力分析

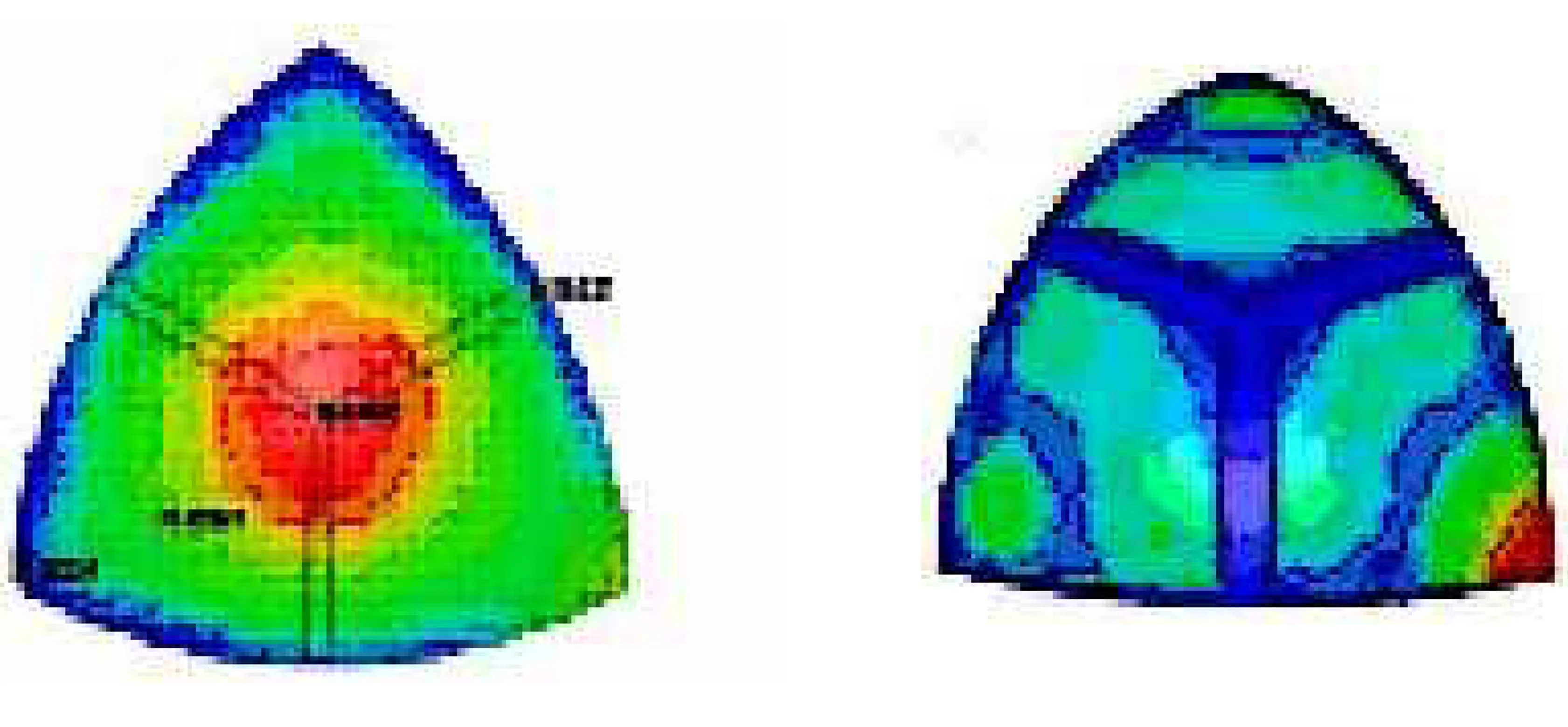
提取了不同时间段，形成碎片的1/8球壳应力云图(见图5)，根据应力云图可以直观的看到随着爆炸时间的变化，容器壁面各单元的受力情况。因为本研究以理想的球罐为研究对象，罐壁受到爆炸载荷作用后，其薄弱点聚集于建模时共节点的连接部位。

图5　不同时刻1/8球罐的应力云图

3结论

本文利用ANSYS/LS-DYNA软件对不同能量载荷下理想球罐的罐壁响应后果进行了模拟分析，结果如下：

(1)在不同的爆炸载荷下，球形容器器壁出现不同的响应后果，因此可以根据在事故现场的容器响应后果来判定发生爆炸时内部载荷的最小临界值，还原事故场景，进而为事故调查提供技术方法和理论依据。

(2)从模拟结果可以看出，发生断裂的部位集中于容器的连接处，离爆点近的薄弱点最容易断裂。

(3)利用能量守恒可以对发生破裂的容器形成碎片过程中不同时刻的动能进行追踪。通过动能追踪，可以确定发生爆炸时碎片可能的飞行范围，该方法可以为工业园区或者化工企业在建设初期进行确定装置的布局时有效防止多米诺事故的发生提供技术手段。

(4)此项研究以理想球罐即单层圆球型作为研究对象，在实际生产过程中球罐有双重球壳、椭圆型球罐等，因此建模过程中各参数的取值如何更接近实际情况是后续研究的重点。

参考文献

[1]余伟炜,高炳军.ANSYS在机械与化工装备中的应用[M].北京：中国水利水电出版社,2006.

[2]王定贤,王万鹏,石培杰，等.柱形爆炸容器动力学响应的有限元模拟与实验检验[J].压力容器,2008,25(7):13-16.

*基金项目：国家自然科学基金(21206064)。

作者简介魏荣宽，主要研究方向为事故模拟、区域安全分析等。

(收稿日期：2014-12-31)

The Numerical Research of the Spherical Vessel Wall Response under Different Energy Load

WEI RongkuanGUAN WenlingGAO TongYIN Xinwei

(CollegeofEnvironmentalScienceandSafetyEngineer,TianjinUniversityofTechnologyTianjin300384)

AbstractStructural fragments are one of the important reasons to cause domino effect in an industrial plant. The study of the vessel wall response law under different energy loading is conducive to analyze structural fragment formation mechanism and the causes of the industrial accident. This study selects spherical vessel as the research object which is commonly used in industrial plants, as a liquid or gaseous storage device. The spherical vessel wall response is simulated under different energy load by the LS-DYNA software. The results show that the vessel wall response is different under different explosion load, so the critical value of explosion load could be determined by the vessel wall response result and also the kinetic energy of structural fragment forming process can be traced by means of energy, providing references for determining a domino effect possibility caused by structural fragments.

Key Wordswall responsespherical vesselenergy loadkinetic energy