橡胶非等温硫化工艺的数值模拟

张韬杰，施 飞

（宁波工程学院 机械工程学院，浙江 宁波 315016）

橡胶硫化是决定橡胶制品质量的关键工序。在硫化过程中，经过高温加热，橡胶流体在硫化剂的作用下发生交联反应，分子结构由链式结构变成网状结构，经一段时间的保压，制品定型，开启模具，取出制品。

橡胶硫化工艺自从1839年被Goodyear发现以后，多年来一直吸引了众多研究人员的注意，特别是利用数值模拟来研究硫化过程。J.C.Ambelang等[1]和H.P.Schlanger[2]利用有限差分方法模拟了轮胎的硫化过程，而G.D.Hubbard等[3]采用有限元法进行数值模拟研究，但他们没有考虑到轮胎从硫化机中取出后在空气中冷却期间的硫化。M.Javadi等[4]和M.H.R.Ghoreishy等[5]以 三 维 瞬时热平衡方程及经验的硫化动力学模型建立了有限元模型来模拟橡胶硫化工艺，通过实验来验证该模型的准确性和可靠性，并讨论了优化硫化时间的一些措施。R.Darwis等[6]基于Gauss-Seidel Red Black和Gauss-Seidel Method的方法开发了数值模拟工具，研究了计算硫化过程中温度场和硫化度场的变化。P.M.Abhilasha等[7]模拟了具有各向异性温度历史的橡胶制品平板硫化的过程，该模型最有意义之处在于能对硫化成型制品的性能进行预测。在国内，刘莉莉等[8]以遗传算法优化了硫化工艺，动态地模拟了非线性、非稳态、多相、强耦合的树脂硫化过程。闫相桥等[9-10]模拟了非均质性、橡胶基复合材料传热性能的各向异性、轮胎硫化时橡胶材料伴有的反应生热及轮胎硫化的实际升温历程。本工作以控制体/有限元（CV/FEM）为基础，对硫化过程的热扩散方程和硫化反应方程进行离散，建立控制方程组，并编写代码，进行数值模拟。

1 基本数学模型

由于在硫化阶段没有橡胶流动就没有对流传热，因此仅考虑橡胶及嵌件与模具之间的热扩散以及橡胶硫化所产生的热量。控制方程包括两类，即：通过热传导和热传递方式进行的热扩散方程以及橡胶硫化方程。

对于三维瞬时热扩散，有：

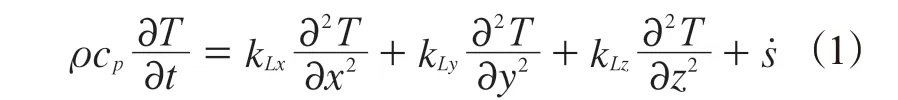
式中，方程左边描述了橡胶的能量变化，右边第1—3项是橡胶在3个方向上的热传导，右边第4项描述了橡胶硫化而放出的热能。其中，ρ为密度；cp为比热容；T为温度；t为时间；kLx，kLy，kLz为橡胶热传导系数；s˙为硫化反应产生的热量，有：

式 中，ΔH为 橡 胶 反 应 热，而G(α,T) =dαdt（Kamal模型[11-13）]。

与之相关的温度边界条件主要分为两类，即第一类边界条件和第三类边界条件。

在第一类边界条件处：T=Tm

在第三类边界条件处：

式中，nx，ny，nz为边界上单位法向量；h为热导率；T∞为边界处模具的温度。

橡胶硫化的反应方程为：

式中，α为硫化度，m为常数，k为Arrhenius类型的温度常数，可以表示如下：

式中，k0为常数，E为活化能，R为气体常数。在求解硫化反应方程时，其初始条件硫化度不能为0，否则方程的解无法收敛。

2 离散微分方程

基于控制体/有限元理论，单元网格按照以下方法进行划分（详见图1）。从图1可以看出，首先将橡胶制品划分为四面体单元，再对四面体单元进行细划分并重新装配组合成新单元，即控制体单元，其既具有有限体积法的一些特性，也具有有限元法的一些功能，可在计算时充分使用它们的特点。

图1 四面体网格的控制体单元

图1中O是四面体单元ABCD的中心，点1，2和3分别是与C相邻的面ABC，BCD，ACD的面中心，点4，5和6分别是与C相邻的边BC，AC，DC的边中点。这样四面体OC26就是C节点控制体与四面体单元ABCD相重合的一部分，同样在与C点相关的其他四面体单元里也具有该相重合的部分，依次将这些重合部分组合叠加起来就组成了节点C的控制体单元。在其他节点处也进行类似运算，就可以得到橡胶制品的三维控制体网格，控制体单元之间没有孔隙，遵循质量守恒定律。此种单元网格各控制体之间关系并非固定，故也称为非结构化控制体网格，对各种形状的零件具有很强的适应性。需要注意的是，在网格划分过程中，最长边与最短边的比例应当尽量接近于1.0，一般不能超过3.0，否则有可能造成计算过程的错误。

按照以上方法，可以得到：

式中，δ可表示为温度、硫化度等场量；Ni为形函数。

对于三维瞬时热扩散方程（1）的离散，在空间上离散是通过差分格式进行的，考虑到求解过程的稳定性，此处采用迎风格式。而对于时间上的离散，此处主要采用全隐式方法进行。各项分别积分得到：

式中，Sc和Sp为s˙进行线性化后的常数；0表示前一次的迭代结果；ΔV为控制体体积；Δt为时间步长。

对积分后的式（4），（5）和（6）进行重新组合[14]，得到如下关系式：

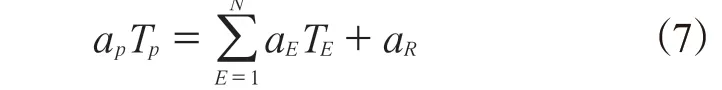
其中：

式中，N为与当前控制体相邻的控制体数目；nxi为控制体单元表面向外的单元法向n的各个分量，λxi为当前控制体和相邻控制体之间连线向量λ的分量。

而温度边界条件的离散，对于第一类边界条件可以直接使用，对于第三类边界条件，可以在相关边界处积分，如式（11）所示。

对于硫化的反应方程（2），可以离散如式（12）所示。

3 计算案例

得到离散方程（7）和离散方程（12）及相关的边界条件后，设计了该数值分析的计算流程图（见图2），并编写了代码。

图2 计算流程

本算例的橡胶制品由橡胶与金属嵌件组成并放置在金属模具中，上下面是第一类边界条件，其余为第三类边界条件。橡胶材料的各参数[5]分别 为：k01.4×1025，m2.91，ΔH4.54×106J·m-3，E260 622 J·mol-1，T0293 K。表1所示为橡胶制品材料的热力学参数[5]。

表1 橡胶制品材料的热力学参数

本算例的橡胶制品图及所划分的四面体网格见图3，热熔系数随温度变化曲线见图4。在计算中选取两点A和D进行比较，位置参数及边界条件见文献[5]。

图3 零件图及划分的网格

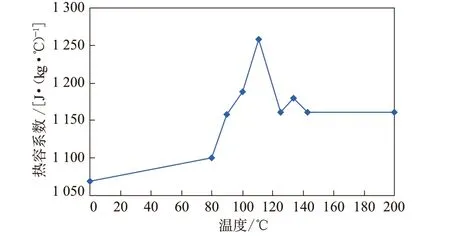
图4 热熔系数随温度的变化曲线

图5所示为本工作代码计算模拟曲线与文献[5]结果曲线比较。从图5可以看出，本文的计算结果与已发表文献的数据是一致的，从而说明了该计算方法是正确的。但预测数据与文献数据尚有些差异，其主要原因在于数值计算方法的不同。

图5 点A和D的硫化度和温度变化曲线

从图5可以看出，在1 800 s左右的时候，A和D两点的硫化度开始迅速增加，此时温度在150 ℃附近，即对于这种橡胶材料，硫化温度在150 ℃左右是合适的。

图6是预测的橡胶制品中面在Z向的硫化历史。由图6可知，硫化过程的发展是非常迅速的，硫化度从接近0到0.99的时间在500 s左右。从图6还可以看出橡胶制品各部分硫化质量的差异。因此，通过对硫化工艺的优化可以很好地控制硫化过程，缩短硫化时间，提高硫化质量。

图6 预测的零件中面在Z向的硫化历史

4 结论

研究发现，模拟橡胶硫化工艺，可以得到零件内温度和硫化度分布图，而无需通过多次实验来测定，减少时间和金钱的浪费，并可以据此优化硫化工艺，降低零件不均匀的温度场和硫化度场，有利于减少零件变形，提高零件的硫化质量。