国债利率期限结构的拟合及预测——基于多项式样条函数

黄 瑞，文忠桥（安徽财经大学 金融学院，安徽 蚌埠 233030）



国债利率期限结构的拟合及预测
——基于多项式样条函数

黄 瑞，文忠桥
（安徽财经大学 金融学院，安徽 蚌埠 233030）

摘 要：本文选择2015年10月至2016年1月交易所国债的日度交易数据，基于三次样条函数法进行利率期限结构拟合，得到五个参数的时间序列.对参数的时间序列建立AR（2）、ARMA（1，1）模型，并对模型做出检验.根据建立的模型，对未来交易日的相应参数作出向前三步预测，得到2016年2月1日到2月3日国债的利率期限结构，据此对相应的债券进行定价，并将其与实际债券价格对比.结果表明，模型对未来债券价格的预测效果良好，误差随着到期期限的增加和预测步长的增加而增大.

关键词：国债利率期限结构；三次样条函数；时间序列；拟合与预测

1 引言

利率期限结构的拟合思想最早由 Cohen，Kramer和Waugh提出［1］，在分段拟合方面，主要采用样条技术，指定样条基函数，将贴现函数表示为基函数的组合，使用回归技术来拟合.McCulloch（1971）［2］最先使用二次样条函数的方法逼近利率期限结构，随后他又提出了三次样条函数的估计方法（1975）［3］.Bliss Waggoner［4］，Bolder［5］和Gusba［6］研究发现，无论是样本内还是样本外，三次样条法均稳定，并且对债券定价也很精确.

在国内，利率期限结构的静态估计方面，陈雯、陈浪南（2000）［7］分别运用一元线性回归和非线性回归方程构建出中国国债市场连续复利的静态利率期限结构.朱世武、陈建恒（2003）［8］设计了三次样条函数分段拟合的方法，并与Nelson-Siegel方法进行比较，实证结果表明三次样条函数拟合结果更好.郭多祚、刘琳琳（2006）［9］的研究表明利用三次多项式样条函数和三次多项式构造中国的国债利率期限结构是有效的.

在利率期限结构的动态估计方面，陈芳菲和沈长征（2006）［10］使用Nelson-Siegel模型估计了水平因素、斜率因素和曲度因素的三因素自回归模型，并对收益率曲线进行预测.胡志强、王婷（2009）［11］基于Nelson-Siegel模型对国债利率期限结构进行了预测，发现模型的短期预测能力较强，长期较弱.文忠桥（2013）［12］采用粒子群算法，运用NS模型，对银行间国债市场的国债利率期限结构进行拟合，得到参数值，并进行预测，结果显示，样本内的预测能力较强，样本外的预测能力较弱.张启坤（2014）［13］对NSS模型中影响利率期限结构的四个因子建立向量自回归模型，研究表明样本外预测效果不佳.赵晶、张洋、丁志国（2015）［14］选取三因子Vasicek模型、三因子CIR模型、多项式样条模型、指数样条模型、DL模型和动态SV模型对中国和美国市场的月度国债收益率数据进行拟合与预测.不同于赵晶等选用月度数据对参数建立AR（1）模型，本文选取日度交易数据得到多项式样条参数的时间序列，分析时间序列的特征，采用AR（2）和ARMA（1,1）模型对参数进行预测，并且根据预测出的利率期限结构为国债定价.

2 多项式样条函数模型

基于用二次多项式作为基函数在估计远期利率曲线可能出现震荡，常采用的改进方法是增加基函数的阶数，因此本文将多项式基函数定为三.根据市场经验，以5年和8年作为分界点，将利率期限结构划分为短、中、长期，构造三次样条函数，假设其贴现因子函数B（0,s）满足：

从（1）式可知，贴现因子函数有12个待定参数.但根据三次样条函数的定义,为保证分段点处的平滑性，得到函数在分段点处的连续性和可导性约束条件：

将上述约束条件代入（1）式，由此，待估参数由12个降低到5个（a1,b1,c1,a2,a3）：

按照连续复利，市场交易国债i的实际价格Pi与理论价格Vi的定价公式［15］分别为：

其中εi，Cti，Bt分别代表国债i的定价误差、t时刻的现金流和t时刻的贴现因子.

参数的估计标准是是样本函数的定价误差最小.考虑到中长期债券价格的波动性要大于短期债券价格的波动，长期债券的定价误差大于短期债券，因此我们选择采用加权最小二乘法，在设定目标函数时加入一个权重系数.设定目标函数为：其中权重系数为国债i的久期的倒数.

3 参数时间序列分析与预测

3.1 数据准备

收集2015年10月到2016年1月国债在交易所每个交易日的交易数据［16］，剔除支付固定单利以及应计利息为负值的国债数据，采用上述三次样条函数模型利用MATLAB软件拟合每个交易日的利率期限结构曲线，得到三次样条函数各参数（a1,b1,c1,a2,a3）组成的时间序列数据.参数的描述性统计结果见表1.

表1 三次样条函数模型参数估计结果的描述性统计

3.2 建立模型（应该首先对参数进行描述性统计分析）

首先，对参数a1,b1,c1,a2,a3进行单位根检验.在有漂移项无趋势项以及SC准则下，得到ADF检验结果（表2）.

表2 参数时间序列数据的ADF检验统计量

参数a1,b1,c1,a2的原始时间序列不平稳，经过两阶差分后序列平稳，这说明滞后项的影响是显著存在的.参数 的时间序列平稳.进一步做出各参数滞后20阶的自相关（ACF）和偏自相关（PACF）图像：

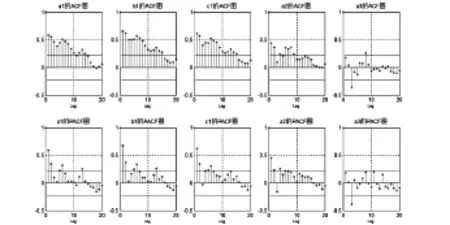
图1 各个参数的自相关和偏自相关图像

对于参数a1,b1,c1,a2自相关图像拖尾，偏自相关图像滞后两阶截尾，说明时间序列服从两阶自回归过程，应对其建立AR（2）模型.而参数a3的自相关和偏自相关图像均近似于滞后一阶截尾，因此，对其建立ARMA（1,1）模型.这与赵晶等人（2015）的研究结果有出入，原因可能是多项式样条模型具有对数据的依赖特征.

模型回归参数均通过t检验，说明回归参数是显著的.对于参数a1,b1,c1,a2的拟合优度较高，都在65%以上，只有对参数a3的拟合优度较低.

3.3 预测

由回归得到的各个模型对相应的参数进行向前三步预测，得到2016年2月1日到2月3日国债利率期限结构三次样条函数各参数的预测数据，并将其与实际数据进行对比：

表4 各参数的预测与实际数据

图2 2015年12月15日预测和实际的利率期限结构

比较各参数的预测和实际数据，发现模型对参数a1,b1, c1,a2的预测误差小，预测效果较好，对参数a3的预测效果较差.由于预测的主要目的是为未来交易日的国债定价，因此，我们由预测的利率期限结构给债券定价得到预测的债券价格，并将其与实际价格对比，作出预测误差的图像见图2，并作出描述性统计见表5.

表5表明了预测误差与债券到期期限之间的关系，即债券预测价格的误差随着到期期限的增加基本上呈增加趋势，且长期债券的预测误差随着预测步长的增加显著增大.对短期债券价格的预测误差基本在1元左右，对中期国债价格的预测误差基本在2—3元，对长期国债价格的预测的平均误差基本在4—6元.

表5 预测定价误差的描述性统计

表6 债券价格预测误差的统计结果

表6表明了债券价格预测误差的表现.预测误差小于2元的债券占60%以上，预测误差小于5元的债券占92%以上.预测误差大于10元的债券约占2%.模型总体的预测效果良好.

误差 2016/2/1 2016/2/2 2016/2/3债券个数 占比 累计占比 债券个数 占比 累计占比 债券个数 占比 累计占比［7,8］ 2 0.0139 0.9722 1 0.0069 0.9583 1 0.0069 0.9583 ［8,9］ 0 0.0000 0.9722 2 0.0139 0.9722 1 0.0069 0.9653 ［9,10］ 1 0.0069 0.9792 2 0.0139 0.9861 4 0.0278 0.9931 10以上 3 0.0208 1.0000 2 0.0139 1.0000 1 0.0069 1.0000总计 144 144 144

综上所述，通过对误差与到期期限的关系以及不同大小的误差的占比两个方面分析，可以得到结论：本文选用的模型的整体预测效果良好，预测误差随着到期期限的增加和预测步长的增加而增大.

4 结论

选择2015年10月至2016年1月交易所国债每日交易的数据，利用三次样条函数对每个交易日的利率期限结构进行拟合，得到参数的时间序列并对其建模.不同于赵晶、张洋、丁志国（2015）对各参数时间序列建立的AR（1）模型，本文对参数a1,b1,c1,a2建立AR（2）模型，对a3建立ARMA（1,1）模型，然后对未来交易日的参数和利率期限结构进行预测，用预测的结果为债券定价.分析债券价格的预测误差，发现模型整体预测效果良好，预测误差随着到期期限的增加和预测步长的增加而增大.

参考文献：

〔1〕K.J.Cohen，R.L.Kramer，W.H.Waugh.Regression Yield Curves for US Government Securities［J］.Management Science，1966，13（4）.

〔2〕J.H.McCulloch.Measuring the Term Structure of Interest Rates［J］.The Journal of Business，1971：19-31.

〔3〕J.H.McCulloch.The Tax-adjusted Yield Curve［J］.The Journal of Finance，1975，30（3）.

〔4〕Bliss R R.Testing term structure estimation methods［J］.Advances in Futures and Options Research，1997，9：197—232.

〔5〕Waggoner D F.Spline methods for extracting interest rate curves from coupon bond prices［R］.1997.

〔6〕Bolder D J，Gusba S.Exponentials，polynomials，and Fourier series：more yield curve modeling at the Bank of Canada［R］.2002.

〔7〕陈雯，陈浪南.国债利率期限结构：建模与实证［J］.世界经济，2000（8）.

〔8〕朱世武，陈健恒.交易所国债利率期限结构实证研究［J］.金融研究，2003（10）：63-73.

〔9〕郭多祚，刘琳琳.三次多项式样条函数在国债利率期限结构研究中的应用［J］.内蒙古财经学院学报，2006（4）：53-55.

〔10〕陈芳菲，沈长征.Nelson-Siegel模型与国债收益率曲线的预测［J］.统计与决策，2006（2）：133-135.

〔11〕胡志强，王婷.基于Nelson-Siegel模型的国债利率期限结构预测［J］.经济评论，2009（6）：57-66.

〔12〕文忠桥.中国银行间国债市场利率期限结构实证分析——基于Nelson-Siegel模型［J］.财贸研究，2013（3）：124-129.

〔13〕张启坤.基于NSS模型的利率期限结构影响因子的时间序列分析 ［J］.赤峰学院学报 （自然科学版），2014（6）：109-113.

〔14〕赵晶，张洋，丁志国.利率期限结构特征的拟合与预测［J］.统计研究，2015（2）：83-89.

〔15〕周子康，王宁，杨衡.中国国债利率期限结构模型研究与实证分析［J］.金融研究，2008（3）：131-150.

中图分类号：F812.5

文献标识码：A

文章编号：1673-260X（2016）06-0116-05

收稿日期：2016-03-18

基金项目：教育部人文社会科学研究项目“‘二次成型’的综合宏观利率期限结构模型估计和应用”（11YJA790162）；国家级大学生创新项目（201510378153）