基于改进突变级数法的地震灾害社会脆弱性风险评价研究
——基于四川地震灾害案例*
2016-07-25徐选华张威威
徐选华,张威威
(中南大学 商学院,湖南 长沙410083)
基于改进突变级数法的地震灾害社会脆弱性风险评价研究
——基于四川地震灾害案例*
徐选华,张威威
(中南大学 商学院,湖南 长沙410083)
摘要:针对地震灾害社会脆弱性评价中指标权重赋值的主观性和传统突变级数评价方法存在冗余指标的问题,首先建立基于突变级数法的地震灾害社会脆弱性评价指标体系,并采用粗糙集属性约简方法改进基于突变级数法的地震灾害社会脆弱性评价指标体系;然后,利用突变级数法对地震灾害社会脆弱性进行评价;最后以四川地震灾害为例,通过对四川省各地区社会脆弱性评价结果进行分析,提出了风险应对建议。
关键词:地震灾害;社会脆弱性;突变级数;粗糙集;风险评价
地震灾害作为一种自然灾害,其破坏力极强,波及范围广,严重威胁到人类的生命安全[1-2]。而中国处于欧亚地震带和环太平洋地震带包围中,地震灾害发生频繁。据统计,2003-2008年,中国发生5级及以上地震265次,6级及以上59次,7级及以上6次,其中2008年发生在四川省汶川的地震,造成69 227人死亡,17 923人失踪,375 783人受伤,灾害直接损失达到8 523亿元[3]。
在当前技术条件下,人们很难准确预报地震的发生,为了减少地震灾害造成的损失,对地震灾害社会脆弱性评估进行研究就显得尤为重要。目前,关于社会脆弱性的概念,由于其具有复杂性,不同学者持有不同的定义,Koks等[4]认为社会脆弱性是社会应对灾害事件的能力;Chen等[5]将社会脆弱性解释为它是一个在预先存在的条件下,影响人们做好灾前准备和从灾后重建中恢复的能力;Clark等[6]认为社会脆弱性是指特定的社会群体、组织或国家,受到灾害冲击的损失程度的大小。
在社会脆弱性评估的问题上,现有的评估方法尚未统一。Cutter[7]在2003年创建了社会脆弱性指标,旨在理解灾害发生时,社会所承担的责任,而后其社会脆弱性思想逐渐被许多学者引用。国外学者,如E.E.Koks等[8]结合灾害性、暴露性及社会脆弱性,将荷兰鹿特丹地区洪涝灾害社会脆弱性进行分区,其评估方法是通过分析总人口、单亲家庭、非欧洲移民、14岁以下人口、65岁以上人口、平均月收入以及平均建筑年限这6个评价指标,并且赋予指标相同的权重计算每个地区的社会脆弱性综合指数;Esfandiar[9]结合因子分析法和网络层次分析法(F’ANP)对伊朗地区地震灾害社会脆弱性进行评估,最后通过空间聚类将社会脆弱性分区,为地震灾害风险管理提供理论依据;Zeng等[10]以广州萝冈区为研究对象,在部分数据不易获得的限制下,提出基于遥感技术的自然灾害社会脆弱性评估模型,并通过分析基于土地使用的人口密度、年龄结构、家户到医院的距离三个指标,并利用专家评估法确定指标权重,最后得出每个地区的综合社会脆弱性指数;在国内,刘德林等[11]以河南省各地市为基本评价单元,运用PCA建立自然灾害社会脆弱性评估模型,并通过AHP法确定指标权重,最后借助ArcGIS软件对评估结果进行了区划制图研究;张永领等[12]从上海市的人口统计和社会经济方面入手,选取45个自然灾害社会脆弱性指标,然后运用主成分分析法选取16个重要指标建立社会脆弱性评估体系,最后采用TOPSIS方法进行评估,为上海市防灾减灾提供科学依据。
综上可以看出,社会脆弱性指标的分类和数量都是非常的巨大,由于社会脆弱性本身具有抽象性和复杂性,所以社会脆弱性评估目前面临两个难题。第一,指标体系的构建。指标体系的构建通常是基于主观经验的,虽然可以证明指标体系具有一定的科学性和合理性,但评价体系中指标信息可能重叠,存在冗余的指标,因此容易造成评价误差。第二,指标权重赋值。以前研究关于权重赋值的方法,如层次分析法、专家咨询法等主观性较强,这种缺陷大大降低了社会脆弱性评估的可信度,从而导致评价结果的可比性较差。
基于上述问题,本文以四川省各地区为研究对象,构建了四川省地震灾害社会脆弱性评价指标体系,并采用粗糙集属性约简法对评价指标进行约简,最后利用突变级数法对地震灾害社会脆弱性进行评价,并提出风险应对建议。
1突变级数方法的改进
1.1问题描述
四川省地形地貌复杂,以山地为主,具有山地、丘陵、平原和高原4种地貌类型,处于喜玛拉牙-地中海地震带上,地震发生频繁,而且波及范围广。根据中国地震灾害大事记,仅2008年我国发生5级以上地震99次,其中发生在四川省省内的达到41次,地震波及地区有汶川、什邡、绵竹、北川、都江堰、攀枝花等地。因此,选择以四川省为研究区域,对各个区域的地震灾害社会脆弱性进行研究,可为防灾减灾提供科学的参考依据。
本文以四川省成都、自贡、绵阳、攀枝花等21个地区为研究对象,参考Cutter[13]和Martins[14]等提出的社会脆弱性评估指标体系,并结合四川省的自身特征与实际情况,选取人口统计、社会经济、建筑和基础设施4个一级指标,人口密度、年龄结构、家庭结构等13个二级指标,以及14岁以下人口比重、14~65岁人口比重等16个三级指标,建立四川省地震灾害社会脆弱性评估指标体系,如表1所示。
表1中,人口密度、14岁以下人口比重、65岁以上人口比重、家庭成员1或2人比例、家庭成员3或4人比例、家庭成员5人以上比例、常住人口女性比例、贫困线下人口比重、失业人口比例、失业人口男性比例、初中学历比例、小学学历比例、平均建筑年限、建筑密度、平均建筑层数这些指标为正向指标;14-65岁人口比重、常住人口男性比例、大学学历比例、高中学历比例、女性参加工作的比例、人均住房面积、卫生机构数、每万人病床数、每万人专业医生数这些指标为负向指标。正向指标表示:指标数值越大,社会脆弱性越大;反之,负向指标表示:指标数值越大,社会脆弱性越小。

表1 地震灾害社会脆弱性指标体系
由于地震灾害社会脆弱性评价指标的量纲和单位不同,而且各指标对社会脆弱性的贡献有正有负,因此为了得到相对统一的量纲,对各指标进行标准化处理。本文采用极差标准化方法对各指标进行标准化处理。
正向相关指标:
Ti=(Xi-Xi,min)/(Xi,max-Xi,min) 。
(1)
负向相关指标:
Ti=(Xi,max-Xi)/(Xi,max-Xi,min) 。
(2)
式中:Xi是指标i的原始值;Xi,max,Xi,min是指标i的原始值的最大值和最小值;Ti是指标i的标准值,其数据值的范围为[0,1]。数据来源于四川省第六次全国人口普查、2014年的四川省统计年鉴(见附表)。经标准化处理后的数据如表2所示。
1.2基于粗糙集属性约简的社会脆弱性评价指标体系约简
地震灾害社会脆弱性评价指标体系可能存在两方面的问题:第一,指标信息之间可能存在重叠,容易造成评价误差;第二,指标权重赋权主观性强。因此本文首先采用粗糙集属性约简方法,
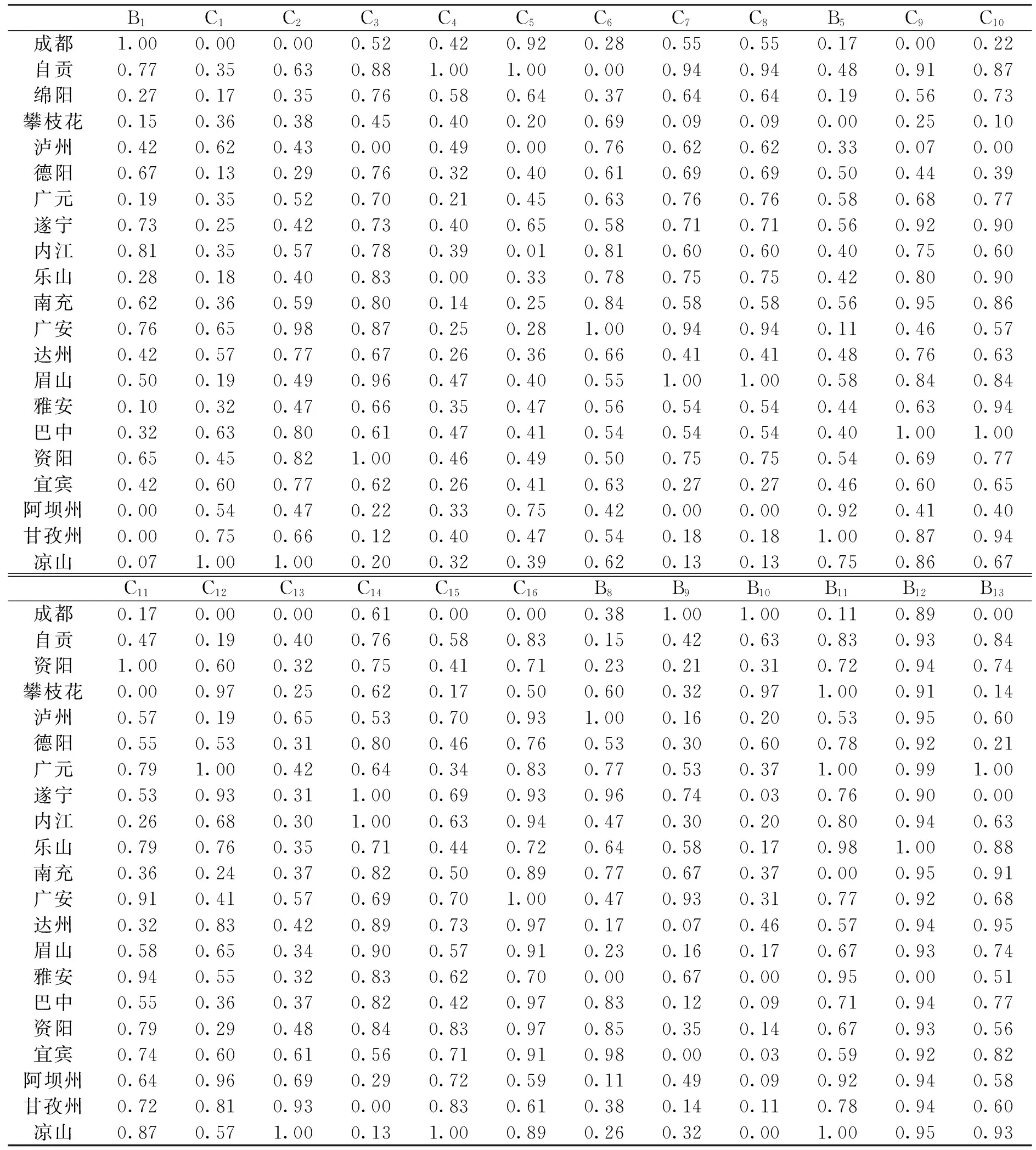
表2 标准化处理后的地震灾害社会脆弱性指标数据
对指标数量和信息进行约简浓缩,使上述评价指标体系更加简化,然后利用突变级数法进行综合评价。
粗糙集属性约简是指在知识库分类能力保持不变的情况下,删除其中不相关或不重要的知识,并不影响原来的知识系统分类,使原有的系统得到简化[15-17]。
定义1:设论域U为非空有限集合,记知识库K=(U,R),其中R为U上的等价关系。
定义2:若非空集合P⊆R,∩P表示P上的不可区分关系,记为ind(P),U/ind(R)表示由等价关系ind(R)划分的所有等价类构成的集合。
定义3:令r为一簇等价关系,r∈R,如果ind(R)=ind(R-{r}),则认为r为R中不必要的,否则称r为R中必要的。
定义4:若P⊆R且P独立,ind(P)=ind(R),则P为R的一个约简。
由于粗糙集理论只能处理离散化的数据,所以在进行属性约简之前应该将数据离散化。本文对每个地震灾害社会脆弱性指标进行K-均值聚类。数据离散化结果见表3。
利用粗糙集属性约简,分别对三级指标进行约简。以二级指标对应的三级指标C12,C13,C14,C15,C16为例。计算过程如下:

表3 地震灾害社会脆弱性指标数据离散结果
注:1,2…20,21分别对应表2中的成都,自贡….甘孜州,凉山。

(3)

(4)

(5)

(6)

(7)
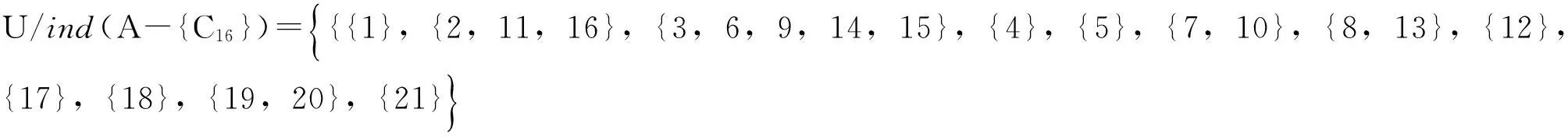
(8)
根据上述计算过程可以得到:
U/ind(A)=U/ind(A-{C13})≠U/ind(A-{C12})≠U/ind(A-{C14})≠U/ind(A-{C15})≠U/ind(A-{C16});

(9)
因此可以约简指标C13,即小学学历人口比例指标应删除。同理,指标C2也应被删除。最后,得到约简后的地震灾害社会脆弱性评价指标体系,如表4所示。
突变理论[18]是一种研究不连续现象的数学理论,该理论由法国数学家Rene Thom创立,其主要思想是根据系统的势函数将临界点分类,进而研究各种临界点附近非连续性状态的特征。突变级数法[19]是根据突变理论中突变模型衍生出来的,该方法是一种对评价目标进行多层次分解,然后利用突变理论中分歧点集方程与模糊数学相结合推导出突变模糊隶属函数,再由归一公式进行综合量化计算,归一公式将系统内部各控制变量不同的质态归化为可比较的同一种质态,最后归一为一个参数,即求出总的隶属函数,从而对评价目标进行排序分析的一种综合评价方法。突变级数法的特点是没有对指标采用权重,但它考虑了各评价指标的相对重要性,从而减少了主观性又不失科学性和合理性。
突变级数模型中,概括起来只有7种性质的基本类型,分别为折叠突变、尖点突变、燕尾突变、蝴蝶突变、双曲脐点突变、椭圆突变以及抛物脐点突变。其中最常见的形式有:尖点突变、燕尾突变和蝴蝶突变,如表5所示。

表5 初等突变模型的势函数
其中x为系统的状态变量,它表示系统的行为状态,这三种突变模型皆只有一个状态变量,a,b,c,d表示该状态变量的控制变量,而重要性由突变模型的内在机制决定,其重要性排序为从左向右。势函数中状态变量和控制变量是相互矛盾的两个方面,系统所处的任一状态既是状态变量与控制变量的统一,也是各控制变量之间相互作用的统一。对于突变模型的势函数f(x),根据突变理论,它的所有临界点集合构成平衡曲面,其方程通过对f(x)求一阶导数而得,即f′(x)=0。它的奇点集通过对f(x)求二阶导数而得,即f″(x)=0,然后再消去x,则可以得到突变系统的分歧点集方程,它表明各控制变量满足此方程时,系统会发生突变。通过将上述分歧点集方程分解,进而导出归一公式,将系统内部各控制变量的不同质态归化为可比较的同一种质态,运用归一公式,可求出表征系统状态特征的系统总突变隶属函数值。常见的3种突变模型的归一公式如表6所示。

表6 常见的三种突变模型的归一公式如下
基于突变级数法的社会脆弱性评价步骤如下所示。
(1)构建地震灾害社会脆弱性评价指标体系。根据评价目的,将评价总目标进行多层次分解。
(2)对底层社会脆弱性评价指标(即控制变量)进行原始数据初始化。归一公式中,控制变量表征的是状态变量的不同方面的特征,其原始数据取值范围和度量单位各不相同,它们之间无法进行相互比较。因此,在使用归一公式之前,采用极差标准化方法对各指标数据进行标准化处理,将控制变量的原始数据转化到[0,1]范围内的无量纲数值。
(3)归一运算。利用归一公式进行综合量化递归运算,从最底层开始算起,直至第一层,求出评价系统的总突变隶属度值。按归一公式可计算出同一层次各控制变量(指标)的相应中间值,对该中间值进行突变级数综合评价时,必须考虑两个原则,即“互补”与“非互补”原则。其中“互补”原则是指系统各控制变量间存在明显的关联作用时,取各控制变量相应的突变级数值的平均值作为总突变隶属函数值;“非互补”原则,若是正向指标,取各控制变量相应的突变级数值的最小值作为突变总隶属函数值,若是负向指标,则取各控制变量相应的突变级数值的最大值作为突变总隶属函数值。
(4)重复上述步骤,分别计算出每个层次社会脆弱性评价指标的突变隶属函数值,从而据此得到总的突变隶属函数值,即社会脆弱性综合评价结果。
我国部分银行费用收益水平存在较大差距,其主要还是费用结构与相关资源配置失衡所致。商业银行加强费用管理,一方面有利于优化资源配置,集中人力、物力、财力进行内部优化,缓和费用对服务价格的不利影响,提升商业银行的经营水平。另一方面可以跟踪业务过程、监控资金使用、处理资源浪费等问题,从而提高商业银行的竞争能力和盈利能力。再次,可集中优势资源,利用互联网金融,以大数据、云计算、社交网络和搜索引擎,改变获客的途径,降低银行的运营成本提高产品创新能力。
2案例应用与分析
2.1地震灾害社会脆弱性综合评价
按照上述突变级数多准则评价方法的计算过程,通过运用归一公式逐步向上综合计算,直至计算出最高层指标的总突变隶属函数值。以成都市为例,数据来源于表2。具体计算过程如下所示。
(1)计算变量B的隶属度
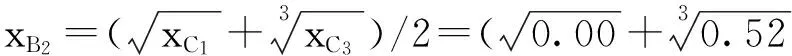

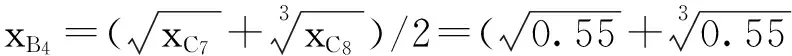


(2)计算变量A的隶属度




(3)计算总的突变隶属度


表7 各地区地震灾害社会脆弱性评价结果
2.2结果与分析
根据上述评价结果,利用ArcGIS10.2软件将社会脆弱性结果划分为五个等级,高(>1.5Std.Dev),中等-高(0.5~1.5Std.Dev),中等(0.5~0.5Std.Dev),低-中等(1.5~0.5Std.Dev),低(<1.5Std.Dev)并绘制四川省地震灾害社会脆弱性区划图(图1)。从图1可直观地分析出四川省地震灾害社会脆弱性的空间分布特征以及分布规律。

图1 四川省地震灾害社会脆弱性分布图
从图1中可以看出,地震灾害社会脆弱性较高的地区主要分布于四川中部地区,如广元、资阳、德阳等地,其中广元市的社会脆弱性值为四川全省最高,因为广元市全市贫困线下人口比重较高,失业率较高,而且医疗条件不发达,卫生机构数、每万人病床数、每万人专业医生数都处于全省最低水平;社会脆弱性中等程度的地区主要集中在四川省西北和东北两地区;社会脆弱性较低的地区主要有攀枝花、成都、雅安等南部地区,其中雅安市社会脆弱性值为全省最低。因为雅安市是2008年四川省特大地震的一个受灾重地,政府及社会在灾后重建中做出了巨大努力。四川省统计年鉴数据显示,在医疗条件方面,每万人病床数、每万人专业医生数均领先于全省其他地区,同时政府及时给予灾民补助,安排就业等一系列措施的实施,极大地降低了贫困人口比重,而且建筑物的平均层数也处于全省较低水平,等等这些指标共同导致了雅安市地震灾害社会脆弱性处于最低水平。因此,提高居民人均收入水平、加大基础服务设施建设,可以有效地降低社会脆弱性。
3结论
四川省地貌复杂,处于地震带上,对地震灾害社会脆弱性进行评价,对于防灾减灾管理具有应用价值。本文在先前对社会脆弱性评估研究的基础上,首先构建了基于突变级数法的地震灾害社会脆弱性评价指标体系,然后采用粗糙集属性约简方法删除冗余社会脆弱性指标,对指标体系进行优化,从而得到最优指标,最后采用突变级数法对地震灾害社会脆弱性评价进行综合评价,克服了社会脆弱性评估中指标主观赋权的局限。通过对四川省各个地区的社会脆弱性的分析,提出风险应对建议。
参考文献:
[1]许冲, 戴福初, 徐锡伟. 汶川地震滑坡灾害研究综述[J]. 地质论评, 2010, 56(6): 860-874.
[2]张金水, 贾增科. 城市地震灾害社会脆弱性评价指标体系研究[J]. 科技致富向导, 2010 (36): 12-14.
[3]聂承静, 杨林生, 李海蓉. 中国地震灾害宏观人口脆弱性评估[J]. 地理科学进展, 2012, 31(3): 375-382.
[4]Koks E E, de Moel H, Aerts J C J H, et al. Effect of spatial adaptation measures on flood risk: study of coastal floods in Belgium[J]. Regional Environmental Change, 2014, 14(1): 413-425.
[5]Chen W, Cutter S L, Emrich C T, et al. Measuring social vulnerability to natural hazards in the Yangtze River Delta region, China[J]. International Journal of Disaster Risk Science, 2013, 4(4): 169-181.
[6]Clark G E, Moser S, Ratick S J, et al. Assessing the vulnerability of coastal communities to extreme storms: The case of revere, MA, USA[J].Mitigation and Adaptation Strategies for Global Change, 1998, 3(1):59-82.
[7]Cutter S L. Vulnerability to environmental hazards[J].Progress in Human Geography, 1996, 20(4):529-539.
[8]Koks E E, Jongman B, Husby T G, et al. Combining hazard, exposure and social vulnerability to provide lessons for flood risk management[J]. Environmental Science & Policy, 2015, 47: 42-52.
[9]Zebardast E. Constructing a social vulnerability index to earthquake hazards using a hybrid factor analysis and analytic network process (F’ANP) model[J]. Natural Hazards, 2013, 65(3): 1331-1359.
[10]Zeng J, Zhu Z Y, Zhang J L, et al. Social vulnerability assessment of natural hazards on county-scale using high spatial resolution satellite imagery: a case study in the Luogang district of Guangzhou, South China[J]. Environmental Earth Sciences, 2012, 65(1): 173-182.
[11]刘德林, 梁恒谦. 区域自然灾害的社会脆弱性评估——以河南省为例[J]. 水土保持通报, 2014, 34(05): 128-134.
[12]张永领, 游温娇. 基于TOPSIS的城市自然灾害社会脆弱性评价研究——以上海市为例[J]. 灾害学, 2014, 29(1): 109-114.
[13]Cutter S L,Finch C. Temporal and spatial changes in social vulnerability to natural hazards[J].PANS, 2008, 105(7): 2301-2306.
[14]Martins V N, E Silva D S, Cabral P. Social vulnerability assessment to seismic risk using multicriteria analysis: the case study of Vila Franca do Campo (S?o Miguel Island, Azores, Portugal)[J]. Natural Hazards, 2012, 62(2): 385-404.
[15]颜艳. 基于粗糙集的属性约简算法及其应用研究[D]. 无锡, 江南大学, 2008.
[16]丁浩, 丁世飞, 胡立花. 基于粗糙集的属性约简研究进展[J]. 计算机工程与科学, 2010, (6): 92-94.
[17]丁斌, 孙政晓, 桂斌. 基于粗糙集与未确知模型的供应商风险评估方法研究[J]. 中国管理科学, 2008(S1): 507-513.
[18]赵旭, 胡斌. 基于突变理论的企业员工反生产行为研究[J]. 管理科学, 2012, 25(4): 44-55.
[19]陈晓红, 杨立. 基于突变级数法的障碍诊断模型及其在中小企业中的应用[J]. 系统工程理论与实践, 2013, 33(6): 1479-1485.
附表:

四川地震灾害社会脆弱性指标原始数据表
*收稿日期:2015-12-07修回日期:2016-01-26
基金项目:国家社会科学基金重点项目(12AZD109);国家自然科学基金项目(71171202)
第一作者简介:徐选华(1962-),男,江西临川人,教授,博士生导师,主要研究方向为决策理论与方法、信息系统与决策支持系统、应急管理与决策、风险分析. E-mail: xuxh@csu.edu.cn
中图分类号:X43
文献标志码:A
文章编号:1000-811X(2016)03-0125-08
doi:10.3969/j.issn.1000-811X.2016.03.021
Risk Assessment on Earthquake Disaster Social Vulnerability Based on Improved Catastrophe Progression Method——A Case Study on Sichuan Earthquake Disaster
XU Xuanhua and ZHANG Weiwei
(SchoolofBusiness,CentralSouthUniversity,Changsha410083,China)
Abstract:For the subjectivity of index weight assignment in the social vulnerability assessment in earthquake disaster, and traditional catastrophe progression evaluation method has the defects of the evaluation of the number of indicators. Firstly, the risk assessment index system of the social vulnerability assessment of earthquake disaster based on catastrophe progression method is established, and rough set attribute reduction method is adopted to improve catastrophe progression method, then using catastrophe progression method to comprehensively evaluate the social vulnerability to earthquake disaster, and finally, take earthquake disaster in Sichuan Province as an example, through the analysis of the results of the social vulnerability risk assessment in Sichuan province, the risk response recommendations is proposed.
Key words:earthquake disaster; social vulnerability; catastrophe progression; rough set; risk assessment
徐选华,张威威. 基于改进突变级数法的地震灾害社会脆弱性风险评价研究——基于四川地震灾害案例[J].灾害学, 2016,31(3):125-132.[XU Xuanhua and ZHANG Weiwei.Risk Assessment on Earthquake Disaster Social Vulnerability Based on Improved Catastrophe Progression Method——A Case Study on Sichuan Earthquake Disaster[J].Journal of Catastrophology, 2016,31(3):125-132.]
