约化Kukles系统的双中心问题及其全局相图的分布
2016-07-24丁维,周俊
丁 维,周 俊
(1.四川大学数学学院,四川成都610064; 2.四川师范大学数学与软件科学学院,四川成都610066)
约化Kukles系统的双中心问题及其全局相图的分布
丁 维1,周 俊2*
(1.四川大学数学学院,四川成都610064; 2.四川师范大学数学与软件科学学院,四川成都610066)
微分方程定性理论的研究起源于常微分方程,由于绝大多数的方程不能求出其精确解,因而需要直接通过微分方程的表达式来研究其性质,其中定性理论在天体力学、生物、化学等领域得到了广泛应用.研究了约化Kukles系统的双中心问题及其双中心条件下系统的全局相图,找到了所有的双中心条件,并分析了在此情形下无穷远平衡点的性质.通过证明八字环的存在性和确定双中心与赤道之间的轨线分布,得到了Poincaré圆盘上的全局相图.
双中心;全局相图;Kukles系统;Poincaré变换
平面微分系统的模型常常出现在流行病学、种群动力学、生化反应及其他应用数学领域[1-6].平面微分系统中,其定性理论的研究已取得丰富的成果,其中一个有趣的问题是寻找系统有多个中心的条件,即多中心问题.寻找一个平面系统具有2个中心的充要条件就是所谓的双中心问题.平面微分系统中,具有双中心的系统有丰富的动力学行为.比如,文献[7-10]给出了具有2个中心的平面微分系统在扰动下极限环个数及其分布.文献[11-12]分别解决了二次系统和三次Z2等变系统的双中心问题.但是对于一般的三次系统的双中心问题还有待解决.
本文研究了约化Kukles系统[13]

的双中心问题及其全局相图,其中x,y,ai,bi∈R.注意到,通过变换x→-x,y→-y,系统(1)化为
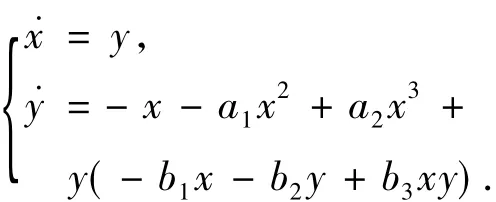
因此,在系统(1)中,只需要考虑a1≥0的情形.第2节中,给出了系统(1)具有双中心的充要条件.在系统的双中心条件下,在第3节中分析了系统(1)在无穷远处平衡点的性质.在第4节中,给出了b3≤0时系统(1)的全局相图分类.
1 双中心条件
在本节中,寻找系统(1)的双中心条件.由文献[14]的定理3.6,原点O:(0,0)是系统(1)的中心当且仅当下面的条件之一成立:
1)b1=0,
2)a1=b2=0,
3)a2=b3=a1+b2=0. (2)
证明 因为平衡点(x0,y0)满足y0=0和-x0,把参数空间分为以下几种情形:当(H1)或(H3)成立时,系统(1)有唯一的平衡点.当(H2)成立时,系统(1)有2个平衡点O和(1/a1,0),其中向量场在(1/a1,0)的雅克比行列式为负值,所以(1/a1,0)是一个鞍点.
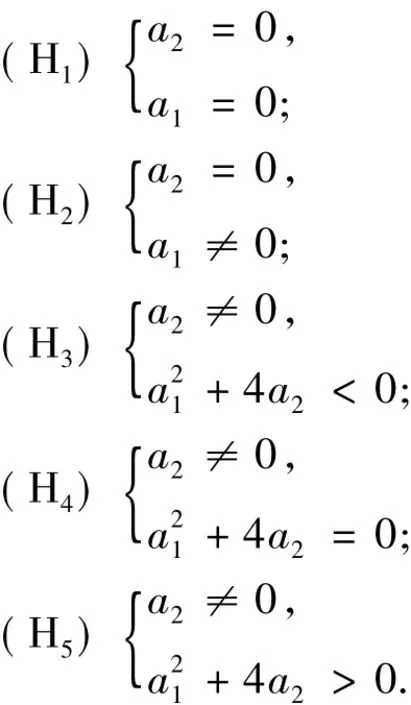
当(H4)成立时,系统(1)有2个平衡点O和(2/a1,0).由文献[14]的定理3.6,O是中心当且仅当b1=0.此时系统(1)化为通过变换x→x+2/a1,y→y,把(2/a1,0)平移到下面系统的原点


由文献[15]第2章的定理7.3得,系统(4)的平衡点O是尖点,则系统(3)的平衡点(2/a1,0)也是尖点.因此,系统(1)至多有一个中心.
当(H5)成立时,系统(1)有3个平衡点O,A: (a,0)和B:(b,0),其中

如果a1=0,向量场在A处的雅克比行列式为负值,所以A是鞍点.相似地,可以证明B也是鞍点.因此,系统(1)在a1=0时至多有一个中心.
定理1.1 系统(1)存在双中心当且仅当

双中心分别在原点和(b,0)且都是非退化的,其中b由(5)式给出.
证明 由引理1.1的证明得,系统(1)有3个平衡点O,A:(a,0)和B:(b,0),其中a,b由(5)给出.向量场在A和B的雅克比矩阵分别是:
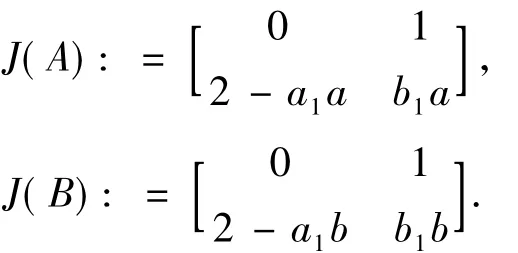
从而,trace(J(A))=b1a,trace(J(B))=b1b.当O不是中心时,如果A、B是中心,则b1a=b1b=0,即b1=0.另一方面由(2)式知O是中心,这与O不是中心矛盾,所以系统(1)至多有一个中心.因此,如果系统(1)有双中心,则O一定是中心.则由(2)式和引理1.1可得,在系统(1)中b1=0.即系统(1)化为
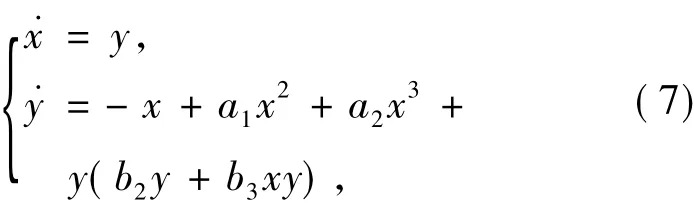
可得J(A)和J(B)的行列式分别是
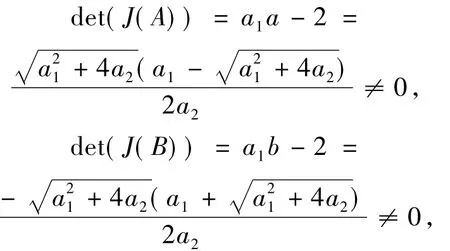
从而,A和 B都是非退化的.由det(J(A))和det(J(B))的表达式知,a2>0时,A和B都是鞍点; a2<0时,A是鞍点.下面寻找a2<0时系统(7)中平衡点B是中心的充分条件.由变换x→b+x/(a1b,把B平移到下面系统的原点
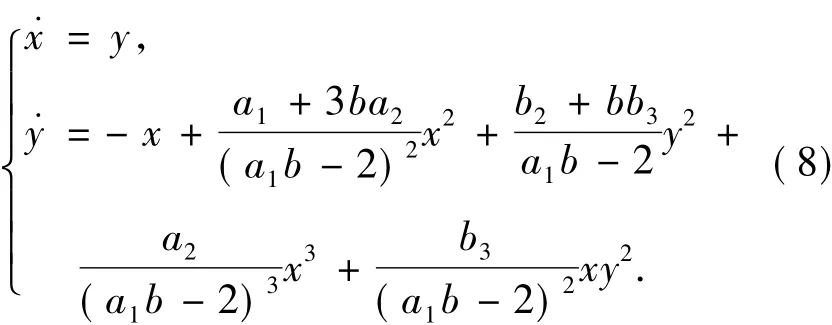
由文献[14]的定理3.6,系统(8)的平衡点O是中心.因此系统(7)的平衡点B也是中心.因此,系统(1)有双中心当且仅当
在定理1.1中,得出系统(1)有双中心的充要条件,且确定了其坐标.注意到在系统(1)中,如果a1<0,双中心分别是原点和(a,0),其中a由(5)式给出.
2 无穷远处的平衡点
本节讨论系统(1)满足双中心条件(即定理1.1中(6)式成立时)和b3≤0时无穷远处平衡点的性质.
定理2.1 当(6)式及b3≤0时系统(1)在无穷远处有2个平衡点C+和C-,其中C+和C-都是退化的且都在y轴上.而且当(b2,b3)∈I∪IV时,C±的小邻域由双曲部分组成,如图1(a)所示;当(b2,b3)∈II∪III时,C±的小邻域分别由双曲部分和抛物部分组成,如图1(b)~(c)所示,其中
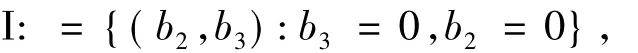

证明 作Poincaré变换x=1/z,y=u/z和dt= z2dτ,系统(1)化为作变换x=v/z,y=1/z和dt=z2dτ,系统(1)化为
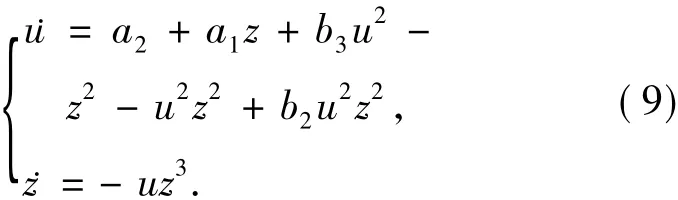
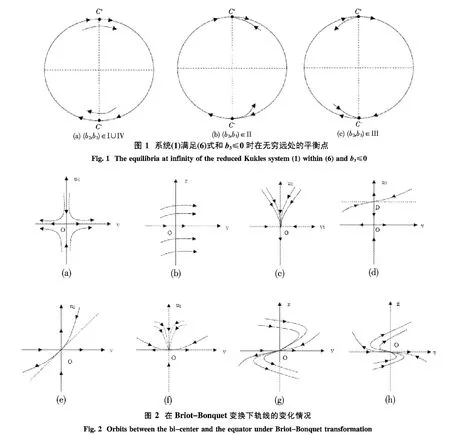

显然,系统(9)在u轴上没有平衡点,也就是说,如果系统(1)在无穷远点存在平衡点,则平衡点肯定在y轴上.
为了考虑系统(1)在y轴上的无穷远处的平衡点,需要考虑系统(10)的平衡点O,其与系统(1)在无穷远处的平衡点C±相对应.对系统(10)作极坐标变换v=r cos θ,z=r sin θ可得

其中,G(θ)=-sin3θ,H(θ)=-b3cos θ-b2sin θ +cos θ sin2θ.显然,系统(10)的特殊方向是θ=0和θ=π.
当(b2,b3)∈I∪II时,H(θ)=cos θ sin2θ-b2sin θ且H(0)=H(π)=0.作Briot-Bouquet变换v→v,z→u1v和时间尺度变换ds=vdτ,系统(10)化为

在u1轴上,系统(12)有一个平衡点(0,0).把系统(12)化为极坐标形式,得到形如(11)的方程.当(b2,b3)∈I时,G(θ)=sin θ cos θ(-2 sin2θ+a2cos θ2),H(θ)=-sin4θ+cos2θ sin2θ-a2cos4θ;当(b2,b3)∈II时,G(θ)=b2cos θ sin2θ,H(θ)=-b2cos2θ sin θ.(b2,b3)∈I时,G(θ)有4个零点0,π/2,π和3π/2.因为G'(0)H(0)=G'(π)H(π)=-<0,G'(π/2)H (π/2)=G'(3π/2)H(3π/2)= -2<0,由文献[15]的第2章定理3.7得,系统(12)分别有唯一的轨线沿着θ=0和θ=π离开O并分别有唯一的轨线沿着θ=π/2和θ=3π/2进入O.因此系统(12)在O附近的的轨线如图2(a).由文献[15]的第2章引理7.1,得到系统(10)在O附近的的轨线如图2(b).
当(b2,b3)∈II时,G(θ)有4个零点0,π/2,π,3π/2且H(0)=H(π/2)=H(π)=H(3π/2)=0.对系统(12)分别作变换v→v1u1,u1→u1,dσ=u1ds和v→v,u1→u2v,dσ=vds,把系统(12)分别化为

和
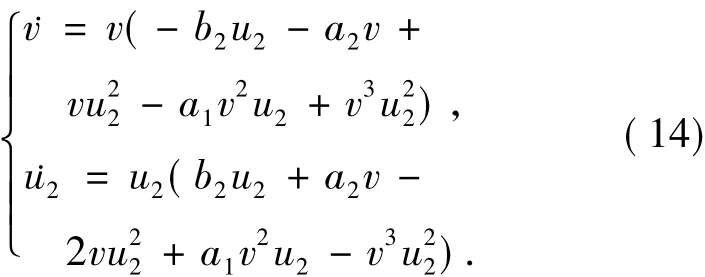
系统(13)和(14)在v1轴和u2轴上分别有唯一平衡点(0,0).由文献[15]的第2章定理7.1,系统(13)的平衡点O是一个鞍结点.所以系统(13)在平衡点O附近的轨线如图2(c)所示.把系统(14)化为极坐标形式,得到G(θ)=2 cos θ sin θ(b2sin θ +a2cos θ),H(θ)=b2sin3θ-a2cos3θ+a2cos θ sin2θ-b2cos2θ sin θ.G(θ)=0的根分别是0,π/2,π,3π/2,arctan(-a2/b2),π +arctan(-a2/b2),且G'(0)H(0)=G'(π)H(π)=-<0,G'(π/2)H(π/ 2)=G'(3π/2)H(3π/2)=-<0.由文献[15]第2章定理3.7,系统(10)分别有唯一的轨线沿着θ=0和π/2离开O并分别有唯一的轨线沿着θ=π和3π/2进入O.因为作变换v→v,u2→u3v,dω=vdσ,系统(14)化为
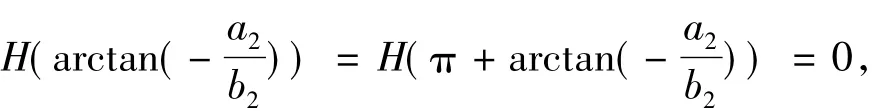

系统(15)在u3轴上有2个平衡点O和D:(0,-a2/b2),其中O是鞍点.为了研究平衡点D的性质,作变换v→v,u3→u3-a2/b2和ω→-2-1a-12ω,把D平移到下面系统的原点其中


3a2)v2+o(v2),使得f(v)+Q1(v,f(v))=0.因为2(d).因此,系统(14)的相图如图2(e).由系统(13)的相图(如图2(c))和系统(14)的相图(如图2(e)),得到系统(12)的相图如图2(f).最后,得到系统(10)的相图如图2(g).
与(b2,b3)∈II的情形相似,当(b2,b3)∈III时,系统(10)在平衡点O附近的轨线如图2(h).
当(b2,b3)∈IV时,G(3)(0)H(0)=G(3)(π)H(π) =6b3<0.由文献[15]的第2章定理3.7,系统(10)分别有唯一的轨线沿着θ=0离开O和沿着θ =π进入O.因此,系统(10)在O附近的轨线如图2(b)所示.最后,得到系统(1)满足(6)时在无穷远处的相图如图1(a)~(c),它们分别和图2(b)、(g)、(h)对应.
3 全局相图
由第2、3节得到的平衡点性质,在本节给出系统(1)满足(6)时的全局相图.
证明 显然,系统(1)有一个首次积分2
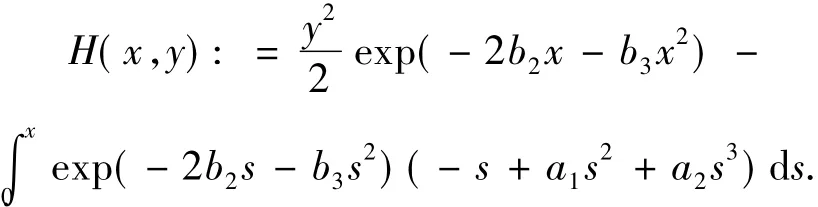

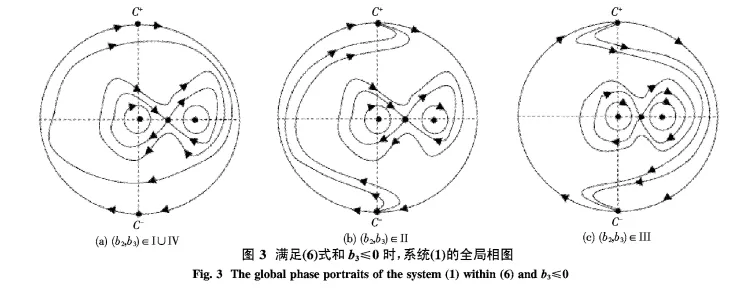
其中,(a,0)是系统(1)的鞍点.因此,没有轨线连接(a,0)和C±.即系统存在一个双同宿轨(或称八字形环).另一方面,所有双同宿轨外的轨线是周期的.否则,由H的解析性,非周期轨道的存在性意味着H(x,y)是一个常量.进一步,由定理1.1和2.1所给出的平衡点性质,得到系统(1)的全局相图如图3.
在定理3.1中给出了满足(6)式和b3≤0时系统(1)的所有的全局相图.b3>0时,与第3节相同的方法,也可以得到满足(6)时系统(1)在无穷远处平衡点的性质.也就是说,平衡点附近的轨线是清楚的.但是,在Poincaré圆盘上,很难确定有限远处的平衡点和赤道之间区域上的轨线分布.另一方面,一类具有双中心的约化Kukles系统的全局相图在文献[16]中被给出.具体地,如同在文献[16]的第3部分开始部分指出的一样,此系统除了满足双中心条件,还对b2(文献[16]中的a3)有一个限制.
致谢 四川师范大学博士科研启动一般项目(2015KYQD314)对本文给予了资助,四川大学数学学院陈兴武教授对本文给予了指导与帮助,谨致谢意.
易得

[1]彭梅,李传东,何兴.基于直接免疫的SEIR计算机病毒传播模型[J].重庆师范大学学报(自然科学版),2013,30(1): 78-80.
[2]杨文川,杨志春.一类具有两斑块效应的SIS传染病模型的稳定性分析[J].重庆师范大学学报(自然科学版),2015,37(5):82-84.
[3]苗宝军,梁庆利.具有Beddington-DeAngelis功能反应函数捕食模型正稳态解存在性[J].四川师范大学学报(自然科学版),2014,32(5):332-337.
[4]邵翠,陈文彦.带有Sigmoidal型响应函数反应扩散模型的正解[J].四川师范大学学报(自然科学版),2013,36(4): 535-539.
[5]陈和柏,石勇国.FitzHugh神经系统中无穷远奇点及闭轨的存在性[J].四川师范大学学报(自然科学版),2013,20(1): 18-22.
[6]徐昌进.一类离散多种群合作与竞争的捕食者与食饵模型的周期解[J].重庆师范大学学报(自然科学版),2015,32(2): 58-63.
[7]COLL B,LI C,PROHENS R.Quadratic perturbations of a class quadratic reversible systems with two centers[J].Discrete Contin Dyn Syst,2009,24:699-729.
[8]ILIEV I D,LI C,YU J.Bifurcation of limit cycles from quadratic non-Hamiltonian systems with two centers and two unbounded heteroclinic loops[J].Nonlinearity,2005,18:305-330.
[9]LIU C.The cyclicity of period annuli of a class of quadratic reversible systems with two centers[J].J Diff Eqns,2012,252: 5260-5273.
[10]SONG Y.The Poincare bifurcation of a class of quadratic system[J].Pure Appl Math,2004,42:160-163.
[11]LI C.The quadratic system which has two centers[J].Acta Math Sin,1985,28:644-648.
[12]LIU Y,LI J.Complete study on a bi-center problem for the Z2-equivariant cubic vector fields[J].Acta Math Sin,2011,27: 1379-1394.
[13]KUKLES I S.Necessary and sufficient conditions for the existence of a center[J].Dokl Akad Nauk,1944,42:160-163.
[14]CHRISTOPHER C J,LLOYD N G.On the paper of Jin and Wang concerning the conditions for a center in certain cubic system[J].Bull London Math Soc,1990,22:5-12.
[15]ZHANG Z,DING T,HUANG W,et al.Qualitative Theory of Differential Equations[C]//Transl Math Monogr.Providence:Am Math Soc,1992.
[16]WU Y,CHEN G,YANG X.Kukles system with two fine foci[J].Ann Diff Eqns,1999,15:422-437.
Bi-center and Global Phase Portraits of the Reduced Kukles System
DING Wei1,ZHOU Jun2
(1.College of Mathematics,Sichuan University,Chengdu 610064,Sichuan; 2.College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)
The study of the qualitative theory of differential equations originated ordinary differential equations.Since the accurate solutions for many complex equations can’t be obtained,we need to study the properties of the equations.The qualitative theory is used in the field of celestial mechanics,biology,chemistry and so on.In this paper we study the bi-center problem of the reduced Kukles system and its global phase portraits.We have found all bi-center conditions and analyze the equilibria at infinity.After proving the existence of figure eight-loop and determining all orbits between the bi-center and the equator,we obtain the global phase portraits on the Poincaré disc.
bi-center;global phase;Kukle system;Poincaré transformation
O175.1
A
1001-8395(2016)04-0508-06
10.3969/j.issn.1001-8395.2016.04.008
(编辑 周 俊)
2015-10-30
四川省教育厅自然科学一般项目(16ZB0063)
*通信作者简介:周 俊(1982—),男,助理研究员,主要从事微分方程与动力系统的研究,E-mail:matzhj@126.com
2010 MSC:34C05;34C07;34C37
