环的整体强无挠维数与STH环
2016-07-24陈勇君王芳贵陈幼华
陈勇君,王芳贵,陈幼华
(四川师范大学数学与软件科学学院,四川成都610066)
环的整体强无挠维数与STH环
陈勇君,王芳贵,陈幼华*
(四川师范大学数学与软件科学学院,四川成都610066)
设R是任何环,D是右R-模.若对任何平坦维数有限的左R-模M,有,则D称为强无挠模.利用模的强无挠维数和环的整体强无挠维数对环进行刻画,引入了st
-VN正则环和STH环的概念.
强无挠模;强无挠维数;整体强无挠维数;st-VN正则环;STH环
本文恒设R是有单位元的结合环,fdRL和pdRL分别表示R-模L的平坦维数和投射维数,F∞表示平坦维数有限的左R-模类,l.gl.dim(R)和w.gl.dim(R)分别表示环R的左整体维数和弱整体维数,r.stf.dRN表示右R-模N的强无挠维数,r.stf.dim(R)表示环R的(右)整体强无挠维数,RM和MR分别表示左R-模范畴和右R-模范畴,其他相关符号可在文献[1]中找到.
J.Z.Xu[2]引入了强无挠模的概念.右R-模D称为强无挠模,是指对任何平坦维数有限的左R-模 M,有.Reza[3]在交换Noether环上讨论了R-模N在什么条件下是强无挠模.S.Reza[4]继续在环R是交换Noether局部环的条件下对强无挠模进行了研究.
H.Y.Yan[5]着重在一般非交换环上对强无挠模的性质进行了研究,并给出了R-模N的强无挠维数(stf.dRN)的定义.右R-模N的强无挠维数,是指使得0→Dn→Dn-1→…→D1→D0→N→0正合,且每个Di都是强无挠R-模的最小非负整数n.如果没有这样的整数n存在,则记r.stf.dRN=∞.文献[5]还给出了R-模N的强无挠维数的另一等价定义,是指使得的最小的非负整数n,其中M∈F∞.2016年,文献[6]遵循H.Y.Yan[5]的思路定义了环的(右)整体强无挠维数(r.stf.dim(R)).设R是环,定义
r.stf.dim(R)=sup{r.stf.dRN|N∈MR},为R的(右)整体强无挠维数.
关于模的强无挠维数的讨论在文献[5-6]中都有表述.本文在这些研究的基础上,按照同调理论的思想利用环的整体强无挠维数来刻画环的结构,且关于任何同调维数的讨论常常是考虑其遗传性,因此自然地去研究强无挠右R-模的子模是强无挠模的环的结构,即r.stf.dim(R)≤1的环.本文在一般非交换的环上应用右R-模N的强无挠维数和环R的(右)整体强无挠维数,引入了st-VN正则环和STH环的概念.
1 st-VN正则环
定理1.1 设φ:R→T是环同态,且T作为左R-模有l.fdRT<∞.若D是强无挠右R-模,则D是强无挠T-模.
证明 设M是任意左T-模,且l.fdTM<∞,由平坦维数的换环定理,有l.fdRM≤l.fdTM+l. fdRT<∞.由于D是强无挠右R-模,故=0.设0→K→F→M→0是正合列,其中F是平坦左T-模.设是自然同态,其中
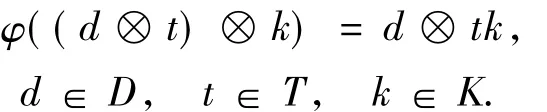
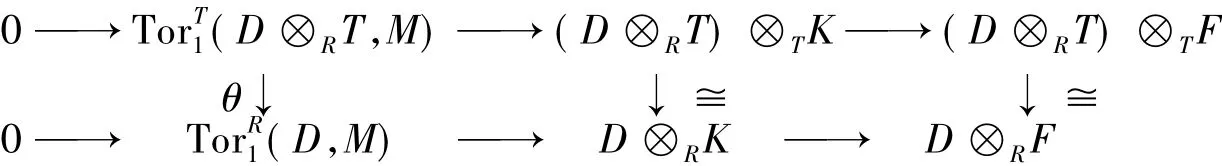
推论1.2 设φ:R→T是环同态,且T是平坦左R-模.若D是强无挠右R-模,则是强无挠T-模.
推论1.3 设R是交换环,a∈R既不是零因子也不是单位.若D是强无挠R-模,则D/aD是强无挠R/aR-模.
推论1.4 设R是交换环,S是R的乘法封闭集.若D是强无挠R-模,则DS是强无挠RS-模.
推论1.5 设R是交换环,D是强无挠R-模,则D[X]是强无挠R[X]-模.
命题1.6 设R是交换环,N是R-模,则
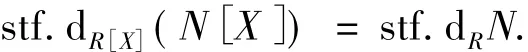
证明 设n是非负整数,若stf.dRN≤n,则存在一个正合列

其中每个Di都是强无挠R-模,i=0,1,…,n.于是

是正合列.由推论1.5知每个Di[X]都是强无挠R[X]-模,i=0,1,…,n,因此
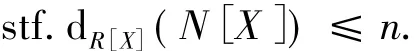
另一方面,令stf.dR[X](N[X])≤n,则存在一个正合列

其中F0,F1,…,Fn-1是平坦R[X]-模,且Fn是强无挠R[X]-模.于是

是正合列.由推论1.3知每个Fi/xFi都是强无挠R-模,i=0,1,…,n.故stf.dRN≤n,因此
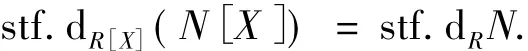
环R称为VN正则环,是指每个R-模都是平坦模.相应的,引入右st-VN正则环的概念来对环进行刻画.
定义1.7 环R称为右st-VN正则环,是指每个右R-模都是强无挠模.
例1.8 1)显然,VN正则环是st-VN正则环.
2)设R=R1×R2是环的直积,则R是右st-VN正则环当且仅当R1与R2都是右st-VN正则环.
定义1.9[8]环R的左finitistic维数和左弱finitistic维数分别定义为
l.FPD(R)=sup{l.pdRM|l.pdRM <∞},和
l.FFD(R)=sup{l.fdRM|l.fdRM <∞}.
容易看到,对任何环R,
l.FFD(R)≤l.FPD(R)≤l.gl.dim(R);
l.FFD(R)≤w.gl.dim(R)≤l.gl.dim(R).
定理1.10 对环R,则以下各条等价:
1)R是右st-VN正则环;
2)r.stf.dim(R)=0;
3)l.FFD(R)=0;
4)对任何M∈F∞,有M是平坦模;
5)每个有限表现右R-模是强无挠模.
证明 1)⇔2)显然.
1)⇔3)由文献[6]推论3.7即得证.
2)⇔4)由文献[6]定理4.6,有r.stf.dim(R) =0⇔对任何 N∈MR,以及任何 M∈F∞,有TorR1(N,M)=0,即M是平坦模.
1)⇔5)显然.
5)⇔4)设X是任意有限表现右R-模,由条件,有X是强无挠模.对任何M∈F∞有=0,故M是平坦模.
回顾环R称为右IF环,是指每一内射右R-模是平坦模[9].文献[9]定理3.5证明了右IF环R是VN正则环当且仅当w.gl.dim(R)≤1.
推论1.11 设R是右IF环,则R有
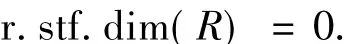
证明 由条件及文献[10]得到l.FFD(R)=0,再由定理1.10,即得证.
推论1.12 设R是环,则以下各条等价:
1)R是VN正则环;
2)l.FFD(R)=0,且w.gl.dim(R)<∞;
3)R是右IF环,且w.gl.dim(R)<∞;
4)R是右st-VN正则环,且w.gl.dim(R)<∞.
证明 1)⇔2)由于R是VN正则环,则
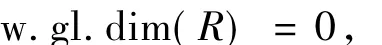
即任意左R-模M都是平坦模.于是l.fdRM=0,故l.FFD(R)=0,得证.
2)⇔1)由条件知:任意R-模都是平坦模,即R是VN正则环.
2)⇔3)由条件知:环R是VN正则环,即任意右R-模都是平坦模,从而环R是右IF环,且
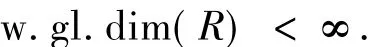
3)⇔2)由于环R是右IF环及推论1.11,知r.stf.dim(R)=0.再由定理1.10知l.FFD(R)=0,即得证.
2)⇔4)由定理1.10,即得证.
推论 1.13 设 R是交换完全环,则 R有stf.dim(R)=0,从而R是交换Artin环,则R有

推论1.14 设R是交换完全环,且
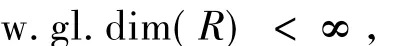
则R是半单环.
证明 由于R是交换完全环,则由文献[7]定理5.7.6知FPD(R)=0.又FFD(R)≤FPD(R)=0,则FFD(R)=0,从而R是st-VN正则环,即每个R-模都是强无挠模.又由于w.gl.dim(R)<∞,由文献[6]命题2.7知每个强无挠模都是平坦模.再由R是完全环,则由文献[7]的定理5.7.4知每一平坦模是投射模,故每个R-模是投射模,因此R是半单环.
2 STH环
环R称为右遗传环,是指每个右R-投射模的子模是投射模,即等价于r.gl.dim(R)≤1.相应的,引入右STH环的概念来对环进行刻画.
定义2.1 环R称为右STH环,是指每个强无挠右R-模的子模是强无挠模,即r.stf.dim(R)≤1.
例2.2 1)显然,右遗传环是右STH环.
2)右st-VN正则环仍是右STH环.
3)若w.gl.dim(R)≤1,则R是右STH环,因此半遗传环也是STH环.特别地,Prüfer整环也是STH环.
定理2.3 对环R,则以下各条等价:
1)R是右STH环;
2)平坦右R-模的子模是强无挠模;
3)自由右R-模的子模是强无挠模;
4)l.FFD(R)≤1;
5)R的每个右理想是强无挠模.
证明 1)⇔2)⇔3)显然.
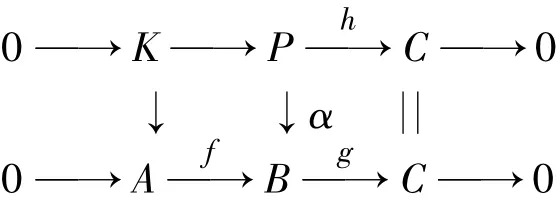
1)⇔4)设任何M∈F∞,X是任意右R-模,则存在一个正合列0→K→F→X→0,其中F是平坦模.于是K是强无挠模,因而有正合列
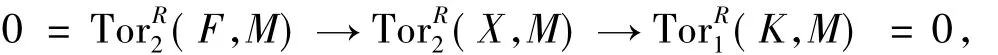
4)⇔2)对于平坦右R-模F的任一子模K,有正合列0→K→F→X→0.对任何M∈F∞,由假设有l.fdRM≤1.因此有正合列

3)⇔5)显然.
5)⇔4)设I是R的任意右理想,M∈F∞,则0→I→R→R/I→0是正合列.由条件,I是强无挠模.于是由同构关系,故l.fdRM≤1,即l.FFD(R)≤1.
推论2.4 设交换环R是STH环,S是R的乘法封闭集,则RS也是STH环.
证明 设M是RS-模且fdRSM<∞,则fdRM= fdRSM<∞.引用定理2.3命题4),得fdRM≤1,故fdRSM≤1,因此RS也是STH环.
定理2.5 设R是环,则以下各条等价:
1)l.FFD(R)=0;
2)l.FFD(R)≤1,且每一内射模是强无挠模.
证明 1)⇔2)由定理1.10即得证.
2)⇔1)设X是任意右R-模,则存在一个正合列0→X→E→C→0,其中E是内射模.由条件,E是强无挠模.又由定理2.3,知X是强无挠模.再由定理1.10,得到l.FFD(R)=0.
引理2.6 设R是交换环,a∈R既不是零因子也不是单位.若FFD(R)≤n,其中n≥1,则
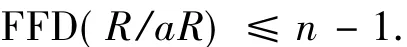
证明 令珔R=R/aR,设M是任意珔R-模且fd珔RM<∞,由文献[7]的定理4.9.7,有fdRM=fd珔RM+1<∞.由条件有fdRM≤n,从而fd珔RM≤n-1,故得证.
定理2.7 设R是dim(R)=1的交换Noether环,则R是STH环.
证明 由于R是Noether环,则由文献[7]的定理6.3.4知dim(R)=FPD(R)=1.再由于FFD (R)≤FPD(R),则FFD(R)≤1,故R是STH环.
定理2.8 设R是环,则以下各条等价:
1)w.gl.dim(R)≤1;
2)R是右STH环,且w.gl.dim(R)<∞;
3)R是右STH环,且每一强无挠模是平坦模.
证明 1)⇔2)对任何右R-模N,则r.stf.dRN≤r.fdRN,故r.stf.dim(R)≤w.gl.dim(R)≤1,故得证.
2)⇔3)由文献[6]的命题2.7即得证.
3)⇔1)设X是任意右R-模,则存在一个正合列0→K→F→X→0,其中F是平坦模.由于R是右STH环,故K是强无挠模,从而K是平坦模,因此w.gl.dim(R)≤1.
推论2.9 设R是交换凝聚环,则以下各条等价:
1)w.gl.dim(R)≤1;
2)R是STH环,且w.gl.dim(R)<∞;
3)R是STH环,且每一强无挠模是平坦模;
4)R是半遗传环.
证明 1)⇔2)⇔3)由定理2.8得证.
1)⇔4)设I是R的任意有限生成理想,由于R是凝聚环,则I是有限表现的.又由于w.gl.dim(R)≤1,则由文献[7]的定理5.5.10有I是平坦模.再由文献[7]的定理3.4.7有I是投射模,故R是半遗传环.
4)⇔1)显然.
推论2.10 设R是Noether整环,则以下各条等价:
1)w.gl.dim(R)≤1;
2)R是STH环,且w.gl.dim(R)<∞;
3)R是STH环,且每一强无挠模是平坦模;
4)R是Prüfer整环,即R是半遗传整环;
5)R是Dedekind整环,即R是遗传整环.
证明 1)⇔2)⇔3)由定理2.8得证.
1)⇔4)参见文献[7]的定理5.5.11.
4)⇔5)显然.
推论 2.11 设 R是 w.gl.dim(R)<∞的Noether整环,则R是STH环当且仅当dim(R)= FPD(R)≤1.
证明 若R是STH环,由推论2.10知R是遗传整环.于是gl.dim(R)≤1,故FPD(R)≤gl.dim(R)≤1.再由文献[11]知dim(R)=FPD(R),故得证.
反之,设dim(R)=FPD(R)≤1,由于FFD(R)≤FPD(R),则FFD(R)≤1.再由定理2.3,故R是STH环.
例2.12 STH环未必是半遗传环.例如:设D是w.gl.dim(D)=1的Prüfer整环,则

其中X是未定元.令R=D[X]/(X2),由引理2.6知FFD(R)≤1,从而R凝聚STH环.用x表示是X在R中的像,而x≠0且x2=0,故x是R的幂零元,因此R不是约化环.又由文献[12]命题1知,w.gl.dim(R)=∞,故R不是半遗传环.
例2.13 STH整环未必是Prüfer整环,Noether的STH整环未必是Dedekind整环.例如:设Q是有理数域,X,Y是未定元,则X2+2Y2是不可约多项式.因此R=Q[X,Y]/(X2+2Y2)是Noether整环,且其Krull维数dim(R)=1.由文献[11]知dim(R) =FPD(R).再由于FFD(R)≤FPD(R),则FFD(R)≤1,故R是Noether的STH整环.由文献[13]的例2.11知,R不是整闭整环,且R是Gorenstein-Dedekind整环,因此R不是Dedekind整环.
[1]ROTMAN J J.An Introduction to Homological Algebra[M].London:Academic Press,1979.
[2]XU J Z.Flat Covers of Modules[C]//Lecture Notes in Mathematics,1634.Berlin:Springer-Verlag,1996.
[3]REZA S.Strongly torsion free,copure flat and Matlis reflexive modules[J].J Pure Appl Algebra,2004,192(1):265-274.
[4]REZA S.Strongly torsion-free modules and local cohomology over Cohen-Macaulay rings[J].Commun Algebra,2005,33(4): 1127-1135.
[5]YAN H Y.Strongly cotorsion(torsion-free)modules and cotorsion pairs[J].Bull Korean Math Soc,2010,47(5): 1041-1052.
[6]陈勇君,王芳贵,熊涛.强无挠模和环的整体强无挠维数[J].四川师范大学学报(自然科学版),2016,39(2):163-167.
[7]王芳贵.交换环与星型算子理论[M].北京:科学出版社,2006.
[8]BASS H.Finitistic dimension and a homological generalization of semi-primary rings[J].Trans Am Math Soc,1960,95(3): 466-488.
[9]JAIN S.Flat and FP-injective[J].Proc AMS,1973,41(2):437-442.
[10]熊涛.由模类Fn确定的同调理论及其应用[D].成都:四川师范大学,2016.
[11]GRUSON L.Critéres de plattitude et de projectivité[J].Invent Math,1971,13:1-89.
[12]王芳贵.平坦的多项式剩余类环[J].数学学报,2002,45(6):1171-1177.
[13]熊涛,王芳贵,胡葵.余纯投射模与CPH环[J].四川师范大学学报(自然科学版),2013,36(2):198-201.
[14]LEE S B.Weak-injective modules[J].Commun Algebra,2006,34:361-370.
[15]ENOCHS E E,HUANG Z Y.Injective envelopes and(Gorenstein)flat covers[J].Algebra Rep Theory,2012,15(6): 1131-1145.
Global Strongly Torsion-free Dimensions of Rings and STH Rings
CHEN Yongjun,WANG Fanggui,CHEN Youhua
(College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)
Let R be a ring and D a right R-module.If TorR1(D,M)=0 for all left R-modules M with finite flat dimension,then D is called a strongly torsion-free.We make use of the strongly torsion-free dimension of a module and global strongly torsion-free dimension of a ring to charaterize rings.Then we introduce the concept of st-VN regular rings and STH rings.
strongly torsion-free modules;strongly torsion-free dimensions;global strongly torsion-free dimensions;st-VN regular rings;STH rings
O154
A
1001-8395(2016)04-0503-05
10.3969/j.issn.1001-8395.2016.04.007
(编辑 周 俊)
2015-05-21
国家自然科学基金(11171240)、教育部博士点专项科研基金(20125134110002)和四川省教育厅自然科学青年基金(15ZB0030)
*通信作者简介:陈幼华(1979—),男,副教授,主要从事交换环与星型算子理论的研究,E-mail:yhchen2006@163.com
2010 MSC:16E10;16E60
