H∞观测器在车用电池SOC估计中的应用研究

刘舒，时珊珊，李雪，张彩萍，高洋

(1.国网上海市电力公司电力科学研究院，上海200437；2.北京交通大学国家能源主动配电网技术研究中心，北京100044)

H∞观测器在车用电池SOC估计中的应用研究

刘舒1，时珊珊1，李雪2，张彩萍2，高洋2

(1.国网上海市电力公司电力科学研究院，上海200437；2.北京交通大学国家能源主动配电网技术研究中心，北京100044)

电池荷电状态(state of charge,SOC)的准确估计是电动车安全运行的重要保证。为了准确估计电池的SOC，将观测器的设计原理应用到电池的等效电路模型中，设计了H∞观测器。以实际容量为90 Ah的新电池为研究对象，在Matlab/Simulink中建立仿真模型实现观测器的计算过程。当新电池运行在DST工况，设定不同仿真初值时，SOC的估计误差绝对值在2%以内，说明H∞观测器不依赖仿真初始值的选择；分析了SOC-OCV曲线对SOC估计精度的影响，得出在SOC估计精度要求很高时，及时更新SOC-OCV曲线是有必要的。

电动车；锂离子电池；SOC估计；H∞观测器

随着电动汽车的发展，电池领域相关技术引起了国内外科研人员的广泛关注。作为体现电池状态的一个重要参数的电池荷电状态(state of charge,SOC)，无法通过直接测量得到，只能测量端电压、电流等间接估算得到。准确估计电池的SOC，可以优化SOC使用区间，避免电池的过充和过放，延长电池的使用寿命[1]。

现有的SOC估计方法中，安时积分法[2]简单易于实现，缺点是比较依赖初始值的选取，而且存在累计误差；开路电压法的特点是利用电池负载电流为零时的开路电压来近似估计电池剩余电量，因为电池开路电压与电池SOC存在一一对应的关系，该方法能够比较准确地估计电池剩余电量，但是在测量电池开路电压时，必须将电池静止一段时间，所以无法实现SOC的在线实时估计；卡尔曼滤波法[3-4]考虑了系统噪声，但是该方法只能用于噪声服从高斯分布情况，一旦研究对象非线性特性稍强或者噪声特性不满足高斯分布时，卡尔曼滤波法估计性能会降低；非线性观测器[5-6]的优点是直接从误差动态的微分方程出发，得到的观测器渐近收敛的充分条件比较简单直观，缺点是不能够简便地给出满足条件的观测器增益矩阵，增益矩阵的选取必须借助于其它的优化算法。

本文设计了H∞观测器估计电池SOC，研究内容包括：SOC初值误差对观测器估计结果的影响；当电池老化前后，H∞观测器的准确性问题。从仿真的结果可以看出：H∞观测器可以适应不同的运行工况；H∞观测器不依赖初值SOC，即使在极限误差条件下亦能以较快速度收敛于真实值，估计误差在2%以内；电池老化前后，H∞观测器精度主要依赖电池SOC-OCV曲线的准确性。

1 参数辨识

状态观测器的核心是状态方程，系数矩阵取值又是状态方程的关键，这些矩阵由状态参数决定，所以电池参数的实时更新尤为重要，电池等效电路模型为参数的实时更新提供了条件。电池模型参数主要有开路电压(open circuit of voltage，OCV)、欧姆内阻、极化电阻和极化电容。

1.1 电池等效电路模型

在本文中，电池的等效电路模型采用Thevenin模型，其中，Ro是欧姆内阻，Rp是极化内阻，Cp是极化电容，UOCV是开路电压，UL是端电压，UR是欧姆压降，Up是极化电压，如图1所示，SOC点每隔5%进行欧姆内阻、极化内阻、极化电容、开路电压的辨识。

图1 Thevenin模型

1.2 参数辨识

为了反映电池对不同电流激励进行响应时，内部参数的变化情况，设计了变电流参数辨识实验，基本涵盖了电池运行电流的变化范围。在Thevenin模型条件下，利用基尔霍夫电压和电流定律得到式(1)～(3)，利用微积分中解非齐次常微分方程的方法，推导了极化电流的解析表达式，如式(4)和(5)所示。

根据(1)～(3)式，可以得到：

式中：Vp(t)为t时刻极化电压值；ip(t)为t时刻流过极化电阻Rp的电流值；Cp为极化电容值；ic(t)为t时刻流过电容Cp的电流值；I(t)为t时刻电池流出或流入电流值。

由于在充放电过程中，电池充放电测试设备的采样时间是0.1 s，所以需要对ip(t)进行离散化处理以得到对应采样时刻的极化电流值。对ip(t)离散化后得到：

式中：ip(t+1)为t+1时刻流过极化电阻Rp的电流值；ip(t)为上一时刻即t时刻流过极化电阻Rp的电流值；I(t+1)为t+1时刻电池流出或流入电流值；I(t)为t时刻电池流出或流入电流值；t是时间常数。

利用以上的理论基础以及非线性最小二乘法，选择合适的时间常数，使相关系数接近1，可以得到对应的这一荷电状态下的开路电压、欧姆内阻和极化内阻以及极化电容。

2 H∞状态观测器设计

2.1 观测器渐近稳定的充分条件[5,7]

Lipschitz非线性系统描述如下：

由上述状态空间方程得到的观测器结构如下：

整理后得到如下方程：

设计观测器目标为：对于给定调节系数g>0(其中g是正常数，通过g的最小值，可以确定增益矩阵L)，设计观测器(9)和(10)，使得误差系统(11)和(12)渐近稳定，并且在零初始条件满足如下不等式：

在设计观测器时，利用式(13)中两个无穷范数的大小关系，去限制观测器的稳定性，所以本文设计的观测器称为H∞状态观测器。

根据鲁棒控制原理，得到渐近稳定的条件：

式中：P=PT，X=P－1L。利用Matlab中LMI不等式工具箱可以得到式(14)的矩阵不等式组的解。

利用文献[6]的方法，可以证明电池系统状态是可观的，可以用观测器的方法估计电池的荷电状态。

2.2 观测器增益的确定[8-9]

观测器的增益L是一个2×1的矩阵，分量L1的作用是对极化电压值进行调节，分量L2的作用是对SOC进行调节。由式(14)可以看出，g2的取值依赖于观测器的系数矩阵，但不同的系数矩阵得到的g2最小值相差不大，故SOC=0.5时的g2最小值可以代表SOC遍历所有值的情况。利用Matlab中LMI不等式工具箱里mincx求解器，确定最小的g2，再利用feasp(·)函数确定稳定范围内的最优增益L。L2/L1决定了收敛速度，L2/L1值越大，收敛越快，而误差曲线波动越剧烈。

3 H∞状态观测器在SOC估计应用中的实现

3.1 基于Thevenin模型的SOC估计状态空间方程[10]

图1是电池的Thevenin等效电路图，其中，UL是电池的端电压，单位是V；UOCV是电池的开路电压，单位是V；Ro是欧姆内阻，单位是Ω；Vp是极化电压，单位是V；Rp是极化电阻，单位是Ω；Cp是极化电容，单位是F；I是电池中流过的电流，单位是A。利用基尔霍夫定律，可以得到以下方程：

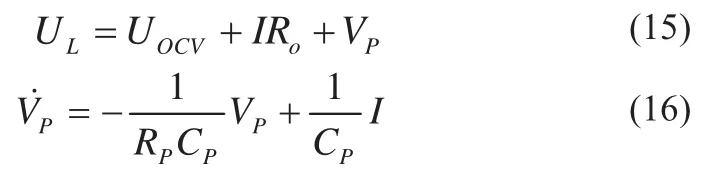
若令系统状态为x1=Vp，x2=SOC，系统的输入u=I，系统的输出为y=UL，则系统的状态方程为：

从图2可以看出，整段SOC区间中，SOC与OCV具有一一对应关系，可以通过线性插值得到不同SOC下的OCV值。

图2 电池充放电SOC与OCV的对应关系

因为y=UOCV+IRo+Vp，其中开路电压是关于SOC的函数，输出方程可变为：

整理得到观测方程为：

式中：C=[1]，D=[Ro]，E=UOCV(SOC)。

由式(18)～(20)可以得到下面的信息：

系统的输入输出为：

系统的状态空间方程为：

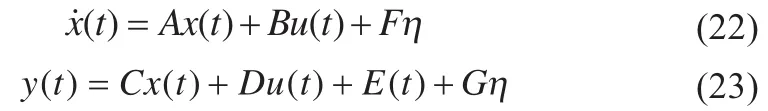
3.2 仿真流程

为了直观了解H∞观测器的工作过程，本文给出了仿真流程图，如图3所示。在本文中，将实验过程得到的SOC值作为SOC真值，后文图中出现的SOC真值即为SOC实验数据。

在图3中，工况数据是实验得到的数据，包含时间、电流、电压以及SOC信息，作为输入输出的真实值。

4 SOC估计精度和影响因素分析

4.1 初值误差对H∞观测器的影响分析

用一节新电池，实际容量为90 Ah的锰酸锂电池做DST工况实验，DST工况电流片段如图4所示，电池从荷电状态SOC=1放电至SOC=0，得到电池的恒流工况实验数据，作为H∞观测器仿真模型的输入，即作为图3的数据输入部分。本节将讨论H∞观测器对不同的仿真初值的响应。在4.1.1和4.1.2中，将H∞观测器仿真模型中的仿真初值SOC分别设定为0.5和0。

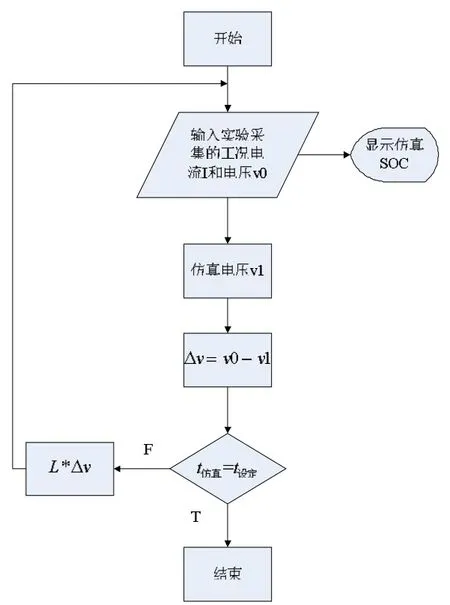
图3 H∞观测器的实现过程

图4 DST工况

4.1.1 初值SOC=0.5

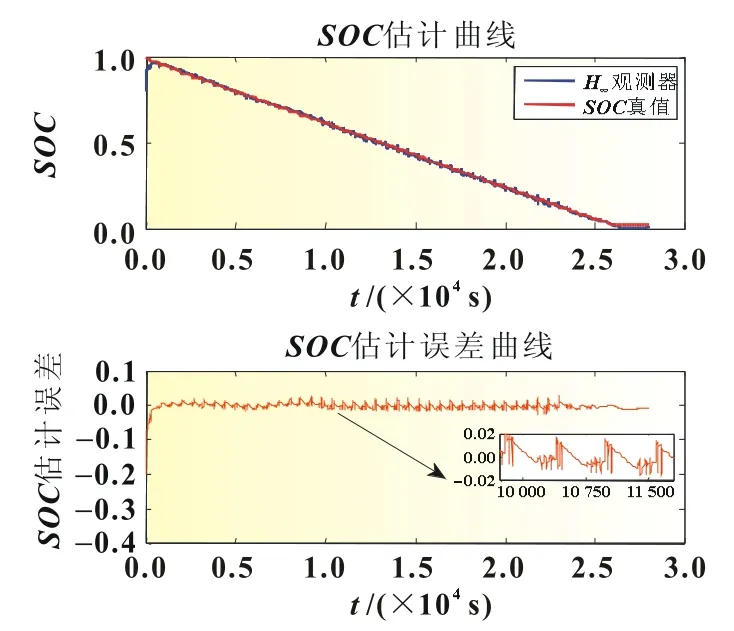
图5的第一个子图对比了SOC真值和H∞观测器估计的SOC；第二个子图给出了H∞观测器估计SOC的误差曲线及部分区间的放大图。从SOC估计误差曲线可以看出，在DST工况下，观测器估计SOC的收敛时间为561 s，收敛精度保证在2%内。

图5 SOC仿真初值为0.5，观测器的收敛情况和估计精度

4.1.2 初值SOC=0

图6的第一个子图对比了SOC真值和H∞观测器估计的SOC；第二个子图给出了H∞观测器估计SOC的误差曲线及部分区间的放大图。从SOC估计误差曲线可以看出，在DST工况下，观测器估计SOC的收敛时间为906 s，收敛精度保证在2%内。

从图5到图6，仿真初值SOC从0.5变化为0，H∞观测器都可以收敛，且SOC估计的绝对误差都在2%以内，可以看出H∞观测器不依赖仿真初值SOC的选取。

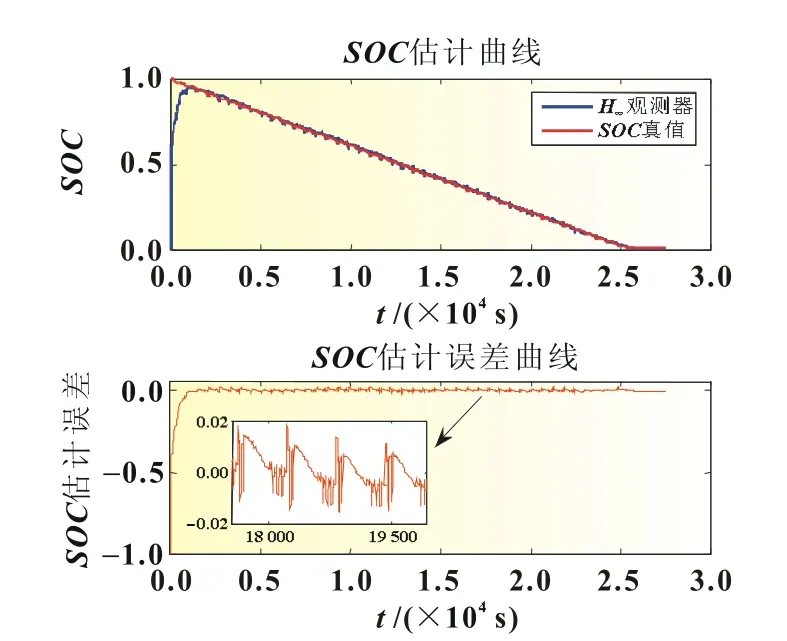
图6 SOC仿真初值为0，观测器的收敛情况和估计精度

仿真初值改变时，收敛时间的变化如表1所示。Δ越小，收敛时间越短，但随着ΔSOC成倍变大，仿真时间并不是呈现线性的增长。因为，t是收敛时间，若不引入电压误差反馈L2×Δy，ΔSOC可以认为是电流相同的安时积分，则收敛时间是随着ΔSOC成倍变化的。H∞观测器引入了反馈L2×Δy，则当仿真初值不同时，同一时刻，SOC查到的OCV不同，所以同一时刻Δy会有差异，L2是常数，则L2×Δy不同；同一时刻，I/Q相同。最终导致同一时刻I/Q+L2×Δy不同，所以收敛时间并不随着ΔSOC成倍变化。收敛时间与ΔSOC具体的定量关系，依赖SOC的仿真初值选择，从图2可看出，因为不同的SOC，对应不同的OCV，当OCV位于两端，收敛速度会较快，但处于平台区，收敛速度会比较慢，当SOC较低时，虽然OCV位于低端，但是要经过平台区，还是拉低了收敛速度。举例分析：当仿真初值SOC为0.5对比仿真初值SOC为0时，仿真初值SOC为0对应的OCV要比为0.5时候的OCV要小，以后同一时刻Δy0.5<Δy0，所以avg(Δy0.5)

收敛时间可以通过：

近似得到，则：

从表1最后两行，可以找到仿真初值SOC为0.5的收敛时间是561 s，仿真初值SOC为0的收敛时间是906 s，确实满足上述的不等式。

?????????????????????? ??????????SOC????/sSOC????/%0.9 0.1 2.3 –2 0.8 0.2 200 –2 0.5 0.5 561 –2 0.0 1.0 906 –2

4.2SOC-OCV曲线对H∞观测器的影响分析

当电池老化后，SOC-OCV曲线发生变化后，H∞观测器是否可以依然具有较好的观测精度，值得研究。本节选用4.1节中选用的同批次且容量已经衰退了5%的旧电池，在实验室充满电，然后做DST工况的放电，直至电压到达下限电压，停止放电，得到旧电池的DST工况实验数据。将旧电池的DST工况实验数据作为H∞观测器仿真模型的输入，即作为图3的数据输入部分。为了不失一般性，将H∞观测器的仿真初值SOC设为0.8。在4.2.1节，将讨论不更新H∞观测器内部SOC-OCV曲线，分析SOC-OCV曲线对观测器估计精度的影响；在4.2.2节，将讨论更新H∞观测器内部SOC-OCV曲线，分析SOC-OCV曲线对观测器估计精度的影响。

4.2.1 不更新H∞观测器内部SOC-OCV曲线

图7的第一个子图对比了SOC真值和H∞观测器估计的SOC，纵坐标为SOC，范围是[0，1]；第二个子图给出了H∞观测器估计SOC的误差曲线及部分区间的放大图，纵坐标是SOC估计的绝对误差，范围是[－0.2，0]。从SOC估计误差曲线可以看出，在当前情况下，观测器最终收敛，但是SOC估计过程误差较大，绝对误差在[－18%，0]。

图7 更新观测器电阻和电容值，观测器的收敛情况和估计精度

4.2.2 更新观测器的SOC-OCV曲线为老化后的值

图8的第一个子图对比了SOC真值和H∞观测器估计的SOC；第二个子图给出了H∞观测器估计SOC的误差曲线及部分区间的放大图。从SOC估计误差曲线可以看出，在DST工况下，观测器估计SOC的收敛时间为310 s，收敛精度保证在2%内。

图8 更新观测器全部参数，观测器的收敛情况和估计精度

从下面三个式子：

可以看出，Δy是由y实验和y仿真决定的，影响了SOC的估计精度和观测器的收敛时间，而实验电压值y实验是已知的，所以y仿真影响了SOC的估计精度和观测器的收敛时间。y仿真是由SOC估计值反馈给观测器，然后通过插值得到UOCV(SOC)、Vp、IRo，通过SOC估计值反馈得到的UOCV(SOC)是随着SOC值非线性变化的一个量，因此UOCV(SOC)的值对y仿真的值影响很大，UOCV(SOC)对SOC的估计精度和观测器的收敛时间有更大的影响。分析得出，电池的SOC-OCV的精度对观测器的SOC估计精度起到了很大的作用。

5 结论

本文将观测器的设计原理应用到电池的等效电路模型中，设计了H∞观测器，分别讨论了不同仿真初值对观测器的影响，以及电池老化对观测器的影响。得出以下结论：

(1)H∞观测器不依赖初值的选择，即使仿真初值SOC设置在极端情况(即仿真初值SOC=0)，观测器依旧可以收敛；

(2)SOC-OCV曲线对于SOC估计精度有很大影响。

[1]POP V,BERGVELD H J,DANILOV D,et al.Battery management systems:Accurate state-of-charge indication for battery-powered applications[M].Eindhoven:Springer Verlag,2008.

[2]李哲，卢兰光，欧阳明高.提高安时积分法估算电池SOC精度的方法比较[J].清华大学学报：自然科学版，2010，50(8)：1293-1296.

[3]温家鹏，姜久春，文峰，等.Kalman算法在纯电动汽车SOC估算中的应用误差分析[J].汽车工程，2010，32(3)：188-192.

[4]ZHANG C P,JIANG J C,ZHANG W G,et al.Estimation of state of charge of lithium-ion batteries used in HEV using robust extended Kalman Filtering[J].Energies,2012,5(4):1098-1115.

[5]ZHANG F,LIU G J,FANG L J,et al.Estimation of battery state of charge with H∞observer:applied to a robot for inspecting power transmission lines[J].IEEE Transactions on Industrial Electronics,2012,59(2):1086-1095.

[6]张云，张承慧，崔纳新.锂离子电池荷电状态估计:非线性观测器方法[J].控制理论与应用，2012，29(12)：1639-1644.

[7]卢建波.Lipschitz非线性系统状态观测器设计[D].青岛：青岛科技大学，2009.

[8]王广雄，林愈银，谢冰.控制问题中的线性矩阵不等式及其求解[J].电机与控制学报，1998，2(4)：191-193.

[9]江兵，郝建国，潘平.Matlab LMI工具箱在教学和科研中的应用[J].电气电子教学学报，2012，34(4)：110-113.

[10]CHEN Z,FU Y H,CHRIS M C.State of charge estimation of lithium-ion batteries in electric drive vehicles using extended Kalman Filtering[J].IEEE Transactions on Vehicular Technology,2013,62(3):1020-1030.

Application ofH∞observer onSOCestimation of lithium-ion batteries in electric vehicles

LIU Shu1,SHI Shan-shan1,LI Xue2,ZHANG Cai-ping2,GAO Yang2
(1.Electric Power Research Institute,State Grid Shanghai Municipal Electric Power Company,Shanghai 200437,China;2.National Active Distribution Network Technology Research Center(NANTEC),Beijing Jiaotong University,Beijing 100044,China)

The accurate estimation of the state-of-charge(SOC)of battery is the basic premise for the effective energy management and the important guarantee for safe and efficient operation for electric vehicles.To accurately estimateSOC,anH∞observer was designed by combining theory of observer with the equivalent circuit model of the battery.A model was built with a new battery of 90 Ah as research object in Matlab/Simulink.When the new battery works on dynamic stress test and different simulation initialSOC,the error keeps bellow 2%,proving thatH∞observer does not depend on initialSOC.The accuracy ofH∞observer depends on the accuracy of the curve ofSOC-OCV.

electric vehicles;lithium-ion battery;SOCestimation;H∞observer

TM 912

A

1002-087 X(2016)08-1570-05

2016-01-24

国网上海市电力公司科技项目资助(52094013502P)

刘舒(1987—)，女，吉林省人，硕士，工程师，主要研究方向为微网及新能源。