模糊数学贴近度在商品选购中的应用

王梓慕

(浙江财经大学数据科学学院，浙江杭州310018)

模糊数学贴近度在商品选购中的应用

王梓慕

(浙江财经大学数据科学学院，浙江杭州310018)

以汽车选购为例，采用模糊数学中模糊模型识别的方法，改进当前电子商务中的购物应用软件.将消费者对事物的期望值进行量化，创建相应的数学模型，改进并完善贴近度算法，最终得到一套在商品选购中最贴近消费者需求的算法.

电子商务;模糊数学;商品选购;贴近度

0 引言

随着社会经济的高速发展，电子商务开始逐渐流行，网上购买商品已然呈现增长趋势.国外的网购运营模式发展早于国内并已趋完善;而国内也发展迅速并逐步被大众尤其是年轻一代所接受［1］.但传统的购物模式已不能满足消费者的需求，消费者需要更加全面的购物信息、更加快速的选购指导、以及更加便捷的购物渠道［2］.本研究探寻一种新型的购物方式，即消费者只需要输入自己的诉求，就可以通过系统算法识别出最适合的商品.这样既提高消费者的效率，统计数据也会给商家提供更准确的消费诉求.

模糊数学是研究和处理模糊性现象的数学方法［3］，在各学科各领域中有着广泛的应用［4－8］，但目前在电子商务选购软件应用方面的研究还比较少，本研究以汽车选购为例，通过模糊数学中模糊模型识别理论的贴近度择近原则，拓展一种新的购物模式，使得网上购物中的购物体验得到改善.

文献［9］提出使用人机交互中用户建模方法来进行汽车的选购，但该方法对用户计算机操作水平和对算法理解有较高的要求，使用起来比较复杂繁琐，在现代电商趋向移动终端的情况下，此方法在移动终端上难以实现.文献［10］提到使用模糊模型识别来选购汽车，但对汽车的要素分析过于宽泛，或是试图用模糊数学的方法给汽车做出一个综合评判、分级［11］.伴随经济的高速发展，汽车不仅仅是一种商品，更代表着一种品味、一种审美、一种文化，甚至是个人内心的完全展示，消费者通过汽车来满足自己的个性和心性的需求［12］.而上述方法都还无法满足现代消费者个性化的需求.

本研究在基于模糊数学中模糊模型识别算法的基础上导出的商品选购方案，以配置繁复、选项超多为特点的汽车选购为例，从易于量化的汽车详细配置入手，使消费者可以通过自己对于汽车配置的需求程度，个性化定制自己需求的目标汽车型号，经过模糊识别的计算，快速获得最接近消费者愿望的目标商品.

1 模糊贴近度原理

1.1 贴近度的概念

贴近度是用来度量两个模糊集合之间的关系密切程度的一种计算方式，取值在［0，1］.贴近度越大说明两个模糊集合之间关系越密切，越小则表明关系越稀疏.数学表述为:设F(U)为论域U的模糊幂集，若映射σ:F(U)×F(U)→［0，1］;(A，B)|→σ(A，B)∈［0，1］，满足条件:

则称σ(A，B)为A与B的贴近度.

1.2 传统贴近度算法

常见贴近度算法求取公式:

n其中:n为样本中的特征值个数，k=1，2，3，…，n;A(xk)为消费者期望的商品特征样本A中的第k个特征值;B(xk)为商品特征样本B中的第k个特征值.虽然利用传统贴近度公式(式(1))可以判断模糊集合的关联程度，但公式(1)也有不足之处，当样本特征值为负时，得到的结果不能产生相应的结论.

为了避免传统贴近度在应用中的局限性，对传统贴近度公式的不足进行了改进.在处理数据过程中优化了数据，在所选范围内尽可能贴近顾客期望值.

2 对算法的改进

2.1 改进依据决策行为

人类的决策行为是众多理性和非理性因素交互作用的结果［13］.Kahneman［14］认为个体在进行决策时依据的不是各种决策方案可能结果的绝对效用值，而是以某个既存的心理中立基点为基准，把决策结果理解为实际损益量与心理参照点的偏离方向和偏离程度.这一点在以购物为目的的决策行为中尤其突出.价值函数曲线［14］对人们的一些决策行为现象做出了合理的解释［13］.

2.2 函数的构造

由于消费者心理比较复杂，也就是会在得与失中产生一个心理价值.基于上述理论和条件，通过计算首先得到心理价值的具体数值，再将其作为特征值与预期购入商品的配置参数进行贴近度计算，构建一个较为贴切的价值函数曲线［14］，函数如下:条件，计算公式为:

式中:n为特征值个数;A(xk)为消费者第k个需求参数通过构建的函数计算得到的心理价值参数;B(xk)为车型第k个配置参数通过计算后得到的参数.

该算法的优势首先在于将各个参数都进行了标准化，使数据在计算前都落在了区间［0，1］.其次，该算法不像传统贴近度算法压缩(放大)了参数在算法当中的作用.例如:车型配置是－1时，进行标准化后为0;当人们的需求为任意数值时，传统贴近度计算得到的结果是0，无法反映出消费者在此项配置当中的需求变化.

3 新旧贴近度算法的比较

为了将改进后的算法与传统算法进行比较，将某一消费者对某品牌车辆的需求参数与该品牌汽车配置数据进行贴近度计算，并对演示计算结果做出比较.

3.1 配置参数

某假定品牌各型车辆的配置参数见表1.告知消费者配置参数的填写要求，即需填写k∈［－1，1］的某一数值，越接近1就表示越需求这一配置，越接近－1就表示越排斥这一配置，通过某消费者的填写得到表2.k代表了该消费者对本件商品的这一特征的需求程度(ka即对特征a的需求程度).某消费者对配置的需求参数见表2.

表1 某品牌车辆配置参数Tab.1Vehicle configuration parameters fora brand

表2 某消费者需求汽车配置参数Tab.2Aconsumer demand parameters for vehicle configuration

3.2 利用两种方法计算

1)传统贴近度算法演示.通过公式(1)计算，得到以车辆C为例的传统贴近度计算结果.

该算法得到的结果有可能会出现负值，然而模糊贴近度的值域为［0，1］，在此值域外的数值无法进行比较，所以在应用过程当中会存在局限性.

2)改进贴近度算法演示.首先，将表1中的配置参数标准化得到表3.再通过公式(2)对消费者需求参数进行计算，得到的改进后消费者需求参数.以车辆C为例(消费者对配置a的需求在公式中表示为消a)算法演示如下:

表3 某品牌车辆配置标准化参数Tab.3Vehicle configuration standardized parameters fora brand

经过计算得到表4.然后通过公式(3)对表3与表4数据进行逐一计算，以车辆C为例，进行算法演示:

表4 某消费者需求汽车配置改进参数Tab.4Aconsumer modified demand parameters for vehicle configuration

3.3 新旧贴近度的计算结果比较

两种方法计算所得结果见表5、表6.从结果可以看出，传统贴近度算法无法计算出可以进行车型比较的近似度结果，在实际使用中具有较大的局限性(σ(表5)［0，1］).而改进后的贴近度模型很好地解决了这个问题(σ(表6)∈［0，1］).表6中数据显示该7种车型经消费者给予不同配置以不同关注程度后，其最大贴近度为0.803 2，根据择近原则，即车型C为最适合此消费者的汽车.

表5 传统贴近度计算结果Tab.5The traditional closeness degree result

表6 改进贴近度计算结果Tab.6The modified closeness degree result

4 实例分析

针对当前汽车购买过程的购买体验，消费者并不是非常满意，各种选配详细繁复，需要花费大量的时间去学习、了解.但是，目前的汽车购买软件界面又非常的简陋，可选配置的数量较少，不能满足消费者的个性需求［2］.本研究将使用上述已经构建好的方法来进行计算并分析其在实际应用中的可行性及优势.

以丰田汽车部分系列的部分配置为数据库进行演示、分析.部分汽车配置详见表7，消费者需求参数详见表8.运用改进后的贴近度算法，将消费者参数与汽车配置进行一一对应计算，消费者与各车的贴近度运算结果见表9.

表7 参数配置表Tab.7Vehicle configuration parameters

表8 消费者需求参数表Tab.8Consumer demand parameters forvehicle configuration

续表8

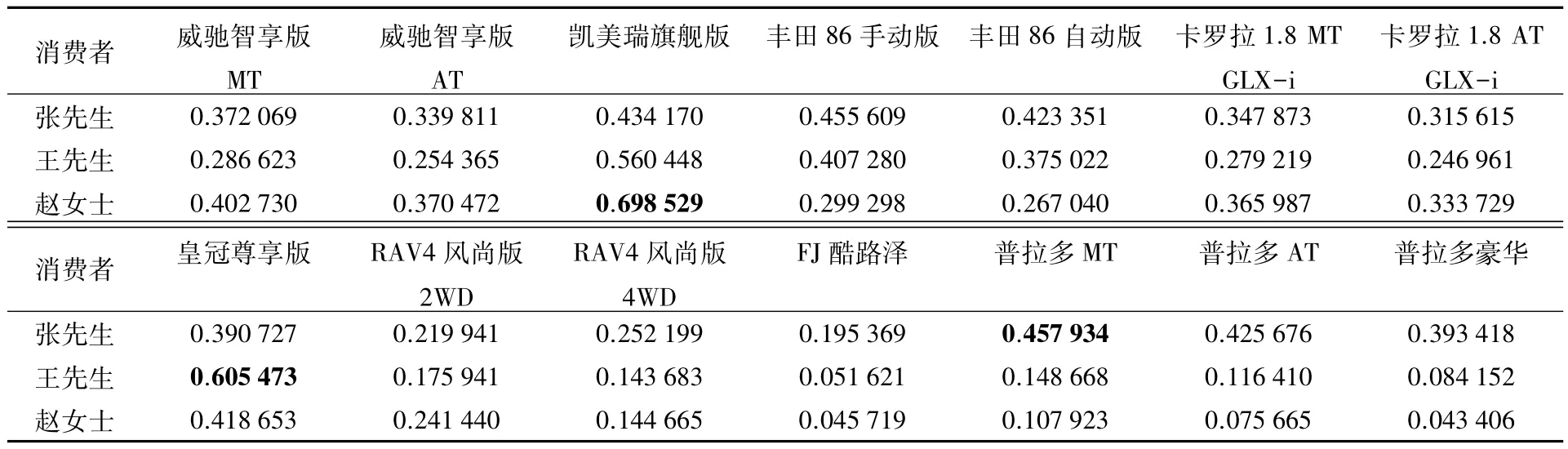
表9 消费者与汽车的贴近度运算结果Tab.9The closeness degree result for consumer demand parameters with vehicle configuration parameters

以上计算结果显示，张先生可能更加青睐普拉多手动版，王先生更加喜好皇冠尊享版，而凯美瑞旗舰版更加适合赵女士的需求.经消费者反馈调查，得到的结果基本符合消费者自身预估.表明改进的贴近度算法最大程度地反应了消费者的需求心理，通过模糊模式识别，可以帮助消费者更加理性地决策自己的消费行为，大幅提升消费者购物体验的满意度和愉悦度.

5 结语

在消费者对事物的期望值进行量化的基础上，通过价值函数理论［14］改进相应的数学模型，打破了传统贴近度算法的局限性，创造了一套可以得出最贴切消费者需求商品的新方法和新思路.为模糊数学在商品选购模式尤其是电商时代菜单式选购中的应用起到了引领作用，为智能终端购物的易用性和提高顾客满意度方面提供了可靠实用的数理依据.

［1］胡永培.基于AHP－模糊方法的淘宝网购综合评价分析［D］.合肥:安徽大学，2011:62.

［2］田真平.我国比较购物模式发展面临的问题及对策研究［J］.商场现代化，2006(29):49－50.

［3］谢季坚，刘承平.模糊数学及其应用［M］.武汉:华中科技大学出版社，2006:249.

［4］王永刚，何士笑.航空公司不安全事件发生率的贴近度研究［J］.中国民航大学学报，2011(1):39－41.

［5］崔汝霞.模糊数学应用软件设计及其在地质评价与识别中的应用［D］.北京:中国石油大学，2008:62.

［6］童英伟，刘志斌，常欢.基于贴近度理论的大气环境质量评价［J］.能源与环境，2008，27(3):115－116.

［7］陈奕，许有鹏.河流水质评价中模糊数学评价法的应用与比较［J］.四川环境，2009，28(1):94－98.

［8］赵玉荣，陈耀华.模糊数学的贴近度和择近原则及其在科研成果评审鉴定中的应用［J］.锦州医学院学报，1994(4): 17－20.

［9］李荣，刘承平.人机交互中用户建模方法的研究［D］.南京:南京师范大学，2004:56.

［10］汪家军.论模糊问题的量化分析与解决方案:汽车选购的数学模型［J］.襄樊职业技术学院学报，2012，11(3):26－28.

［11］傅丽贤，黄会明.基于模糊综合评判的汽车选购决策［J］.金华职业技术学院学报，2015(6):74－78.

［12］孙琳琳.汽车座椅舒适度的创新设计以及主客观评价研究［D］.长春:吉林大学，2014:120.

［13］何贵兵，于永菊.决策过程中参照点效应研究述评［J］.心理科学进展，2006，14(3):408－412.

［14］KAHNEMAN D，TVERSKY A.Prospect theory:an analysis of decision under risk［J］.Econometrica，1979，47(2):408－412.

(责任编辑:林晓)

The application of closeness degree algorithmin shopping

WANG Zimu
(School of Data Science，Zhejiang University of Finance and Economics，Hangzhou，Zhejiang 310018，China)

In this paper，author tries to improve and develop the software and APPs of E－business using the fuzzy model identification in a case study on automobile purchase activity.The author created a new relative mathematical model based on quantizing the expectation of customer，and then established a new closeness degree algorithm via improving and modifying the traditional algorithm.A perfectedalgorithm is acquired which could help consumers make private and unique choice when shopping takes place.

E－business;fuzzy mathematics;shopping;closeness degree

O29

A

10.7631/issn.1000－2243.2016.06.0913

1000－2243(2016)06－0913－06

2016－08－24

王梓慕(1992－)，实习研究员，主要从事应用数学研究，wangzm@tsinghua－tj.org

国家自然科学基金资助项目(71572039)

式(2)中vk为消费者的需求配置参数，该函数的主要特征为在x等于0或者1时函数变化较小，在x等于0.5时变化最快.即当消费者有很小的倾向时，函数变化最快;在消费者接近需求心理饱和时，函数变化较慢(边际效应变化［14］)，见图1.

通过考察度量，用距离型的模糊贴近度算法进行计算比使用传统贴近度算法更加符合本研究的应用