变电站软母线下料长度二分法数值计算模型

黄宴委，王庭桉

(福州大学电气工程与自动化学院，福建福州350116)

变电站软母线下料长度二分法数值计算模型

黄宴委，王庭桉

(福州大学电气工程与自动化学院，福建福州350116)

针对变电站软母线的下料长度问题，提出一种二分法的数值求解模型.首先在假设水平应力已知的条件下，由受力分析建立软母线下料长度的非线性耦合解析模型，进而设计变电站软母线下料长度二分法数值计算模型，并利用二分法得到精确的数值解.仿真与应用结果表明，数值计算模型能够得到非常准确的下料长度，安装后的软导线总弧垂误差均在－2%～+3%以内，具有良好的施工效果.

变电站;软母线;下料长度;非线性耦合模型;数值模型;二分法

0 引言

变电站软母线属于短距离架空线，绝缘子、耐张线夹等金具对变电站内软母线长度和受力有很大影响，明显具有不容忽视的因素［1－2］.在施工中软母线多数采用近似经验公式计算，每次放线前都需试挂修正.文献［3］提出将整串软导线等效为梯形模型，但由于是近似计算，故无法准确计算出软母线的下料长度.文献［4］将软导线分成两端绝缘子串的悬链线部分以及中间导线的平抛物线部分，却没有考虑高差变化的影响.文献［5］采用算术平均数计算挂点之间的档距，等效投影法计算金具绝缘子串的长度，但精度不够高.这些方法均未准确考虑或简要估计绝缘子金具重量对下料长度的影响，计算结果精度不高［6］.

本研究对变电站软导线进行受力分析，假设水平应力和弧垂已知，设计出一种变电站软母线下料长度数值计算模型.经过Matlab仿真计算与实际结果表明，该数值计算模型精确可靠，所得变电站软母线安装后的弧垂误差均在!2%～"3%以内.

1 变电站软导线受力分析模型

如图1所示为变电站软导线受力分析模型.其中，A、B为变电站软导线两悬挂点;以A点为坐标原点建立X－Y坐标系;AE和BF为耐张绝缘子串;EF为软母线;整个软导线的档距为L、高差为H;软母线部分的档距为l、高差为h、最低点为O;C为软母线上任意一点.已知结构参数软导线档距L与高差H，以及材料参数左右两侧耐张绝缘子串的金具个数n和m，各个金具的长度λi和重量gi，软母线截面积s与软母线比载γ，将变电站软导线划分为耐张绝缘子串和软母线两个部分进行受力分析.

1.1 耐张绝缘子串受力分析

假设悬挂点A处支反力RA和任意一点的水平张力T0=σ0×s(σ0为水平应力)已知.在T0作用下，耐张绝缘子串呈现出弦多边形形状.由文献［7］可知耐张绝缘子串的弦多边形模型，n个金具构成的左侧AE段耐张绝缘子串的水平投影长度λo1和垂直投影长度λv1为:

同理假设支反力RB已知，右侧BF段耐张绝缘子串水平投影长度λo2和垂直投影长度λv2为:

由图1可知，E点坐标为(λo1，!λv1)，E点支反力RE，F点坐标为(l"λo1，h!λv1)，F点支反力RF为:

1.2 软母线受力分析

以图1中软母线端点E为原点建立x－y坐标系，以悬链线理论为基础，取任意一段软母线作为研究对象进行受力分析建立软母线的悬链线方程为［7］:

其中:a为软母线最低点O至E点的水平距离.

由E、F两点坐标可知，软母线的档距l与高差h分别为:

将F点坐标(h，l)代入式(4)可得:

软母线上任一点轴向应力的垂直分量σγx可以根据式(4)求得:

将E、F两点横坐标分别带入式(7)可得到软母线E、F两点轴向应力的垂直分量σγE和σγF为:

由于同一点上力的大小相等，软母线上σγE和σγF分别与耐张绝缘子串上RE和RF对应，即RE=s# σγE与RF=s#σγF.因此，由式(3)和式(8)可得到RA、RB的表达式为:

弧长微分公式为:

将式(4)代入式(10)并关于x积分，积分上限为l，积分下限为0，可得软母线下料长度LW为:

式(1)、(2)、(5)、(9)、(11)构成了变电站软母线下料长度解析模型，其中l、h、σ0是未知的.在解析模型中l、h与λo1、λv1、λo2、λv2、RA、RB等中间变量相互耦合，是一组非线性耦合的复杂数学方程组.同时，在施工现场中，水平应力σ0难以测量，也大大限制了该解析模型的实际应用价值.

2 软母线下料长度数值计算模型

数值计算模型具体步骤如下:Ⅰ)给定设计弧垂值f0，弧垂步长二分法调整模块利用二分法构造一个弧垂值中间变量fc作为求解水平应力的依据;Ⅱ)水平应力计算调整模块建立变电站软导线斜抛物线模型，根据弧垂值中间变量fc直接求得水平应力σ0，利用耐张绝缘子串水平投影长度作为循环条件，求得准确的水平应力σ0与支反力RA、RB;Ⅲ)投影长度计算模块在已知水平应力σ0与支反力RA、RB的条件下，利用弦多边形模型计算得到耐张绝缘子串水平与垂直投影长度，最后计算得到软母线的高差h与档距l;Ⅳ)总弧垂计算误差调整模块在已知软母线档距l和高差h的条件下，求得数值模型总弧垂最大值fm，与设计弧垂值f0进行比较，作为弧垂步长二分法调整模块的判断依据，满足误差时保存当前σ0、l、h.Ⅴ)软母线下料长度计算模块在已知准确的水平应力σ0与软母线部分档距l和高差h的条件下，直接计算得到软母线下料长度LW.

2.1 弧垂步长二分法调整模块

给定设计弧垂值f0，构造一个弧垂值中间变量fc和数值求解得到的软导线总弧垂最大值fm.当fm与f0之间存在差异时，利用二分法设计fc的调整律为:

其中:fc和fm的初值均为f0.

2.2 水平应力计算调整模块

在已知弧垂值中间变量fc的条件下，利用耐张绝缘子串水平投影长度作为循环条件，最终得到准确的水平应力σ0与支反力RA、RB.

2.2.1 坐标变换

将软母线端点E从x－y坐标系变换到图1中的X－Y坐标系为:

将式(13)代入悬链线方程(4)中消去x与y，可得到X－Y坐标系中变电站软导线的悬链线方程为:

式中:X的范围是λo1≤X≤L－λo2.任一点的弧垂公式为:

将式(14)代入式(15)可得到基于悬链线的变电站软导线弧垂表达式fx为:

式中的fmax与σ0是非线性关系，无法根据弧垂直接求得水平应力.而为了得到弧垂与水平应力的线性关系表达式，需要对基于悬链线的变电站软导线弧垂表达式(17)进行进一步简化.

2.2.2 斜抛物线模型

式中:X的范围是λo1≤X≤L－λo2.对式(16)关于X求导，并令其等于零，求得fx取最大值时的X值，并将该X值回代入式(16)可得到基于悬链线的变电站软导线弧垂最大值fmax为:

式中:α=arctg h/l为软母线高差角.将坐标变换式(13)代入式(18)，又由假设条件Ⅲ)可知α≈β(β= arctg H/L为软导线高差角)，可以得到变电站软导线斜抛物线模型的弧垂表达式f'x为:

简化基于悬链线的变电站软导线弧垂表达式，建立变电站软导线斜抛物线模型，进而得到弧垂与水平应力的线性关系表达式.

根据图2受力关系，列出力矩平衡方程式，由文献［7］可知软母线的斜抛物线方程为:

其中:X的范围为λo1≤X≤L－λo2.

根据图1软导线的力矩关系，分别列两悬挂点A、B的力矩平衡方程式，由假设条件Ⅳ)可知左右两侧耐张绝缘子串重量相等，即GJ1=GJ2，则两悬挂点处的支反力RA、RB为:

式中:GJ为左右两侧耐张绝缘子串平均重量为软母线荷载集度.由式(20)，式(19)可简化为:

式(21)与式(22)分别是变电站软导线斜抛物线模型的弧垂表达式与其弧垂最大值.

2.2.3 水平应力计算调整模块

在已知弧垂值中间变量fc的条件下，根据弧垂求得水平应力，进而求得支反力.利用耐张绝缘子串水平投影长度作为循环条件，当水平投影长度满足误差范围时，当前得到的σ0、RA与RB是准确的.

由式(22)可知，弧垂与水平应力呈反比关系，对其变形可以得到:k分别为左、右两侧耐张绝缘子串串长;X的范围为λo1≤X≤L－λo2.对式(21)关于X进行求导，并令其等于零，可知当X=L/2时，即在软导线档距中央，可取得弧垂最大值f'max为:

式(23)中弧垂值中间变量fc由弧垂步长二分法调整模块确定，而耐张绝缘子串水平投影长度λo未知，故无法得到水平应力σ0.令λo的初始值为两侧耐张绝缘子串的平均串长，即λo=(λ1"λ2)/2，并且知道fc，利用式(23)可以得到一个水平应力σ0，进而由式(20)确定支反力RA.那么，此时利用耐张绝缘子串弦多边形模型式(1)计算所得的水平投影长度λ'o是相对准确的.由于弦多边形模型是准确的，故当λo与λ'o之间近似相等时，所得λo就是耐张绝缘子串水平投影长度的准确值，此时所得σ0、RA与RB也是准确的.

当λo与λ'o之间存在差异时，利用二分法设计λo的调整律为:＞e，则循环上述四个步骤，否则，保存当前σ0与RA.

同理，根据上述五个操作步骤，可以计算得到右侧耐张绝缘子串的支反力RB，并保存RB.

2.3 投影长度计算模块

在已知σ0、RA与RB的条件下，利用耐张绝缘子串弦多边形模型依次计算出每个金具的水平和垂直投影长度λio、λiv，然后叠加所有金具的λio、λiv就可以得到左、右耐张绝缘子串的水平与垂直投影长度λo1、λv1、λo2、λv2，最后计算得到软母线的高差h与档距l.以左侧耐张绝缘子串为例，耐张绝缘子串由n个金具构成，投影长度计算模块的具体设计步骤为:

i)已知水平应力σ0和支反力RA，并且知道第i个金具的长度λi和重量gi，由式(1)计算出水平投影长度λio和竖直投影长度λiv，直到i=n为止.

ii)叠加所有金具λio和λiv，由式(1)可得左侧耐张绝缘子串的水平与垂直投影长度分别为λo1与λv1;同理，由式(2)可以得到右侧耐张绝缘子串(m个金具)的水平与垂直投影长度λo2、λv2.

iii)在得到λo1、λv1、λo2、λv2之后，由式(5)可以计算得到软母线的档距h与高差l，并保存.

2.4 总弧垂计算误差调整模块

在已知软母线部分档距l和高差h的条件下，由式(6)可以求得a值，分别计算耐张绝缘子串弧垂和软母线弧垂两个部分的弧垂，进而得到数值模型总弧垂最大值.将总弧垂最大值与设计弧垂值进行比较，其

中:λ'o的初始值为λ'o=λo.以左侧耐张绝缘子串为例，水平应力计算调整模块的具体设计步骤为:

1)由式(24)确定一个水平投影长度λo;

2)将弧垂值中间变量fc和λo带入式(23)，并且知道软母线比载γ、档距L，求出水平应力σ0;

3)由T0=σ0×s求出水平张力T0，将T0代入式(20)求出支反力RA;

4)将T0、RA代入式(1)求出悬链线模型水平投影长度λ'o，将λo与λ'o进行比较;

5)给定λo与λ'o差值的误差范围e，若λo－λ'o直到满足误差，保存当前σ0、l、h.

如图1所示，软导线总弧垂分为耐张绝缘子串弧垂f1和软母线弧垂f2两部分，故软导线总弧垂fX为:

由数学几何关系可知，耐张绝缘子串弧垂部分f1为当X取同一个值时，直线AB与EF之间在竖直方向的距离大小，即:式中分别为直线AB、EF斜率.

由于悬链线方程及其有关导出公式是精确计算式，故由式(4)可得软母线弧垂部分f2为:

式中:X的范围是λo1≤X≤L－λo2.

将式(26)、(27)代入式(25)得到变电站软导线数值模型总弧垂fx的表达式:

式中:X的范围是λo1≤X≤L－λo2.对式(28)关于X求导，并令其等于零，可解得总弧垂取最大值时的横坐标Xmax为:

总弧垂计算误差调整模块，具体步骤如下:

i)已知软母线部分档距l和高差h，并且知道水平应力σ0、软母线比载γ，由式(6)可以求得a.

ii)计算耐张绝缘子串弧垂f1和软母线弧垂f2，得到数值模型总弧垂fX.

iii)由式(29)求得总弧垂取最大值时的横坐标Xmax，将l、h、a、Xmax代入式(28)求得软导线总弧垂最大值fm.

iv)给定fm与f0差值的误差范围ef，将总弧垂最大值fm与设计弧垂f0进行比较.若fm－f0＞ef，则回到弧垂步长二分法调整模块对弧垂值中间变量fc进行二分法调整，按照五个模块的顺序重新计算出新的总弧垂最大值fm，再进行新的比较;否则，保存当前σ0、l、h.将σ0、l、h直接代入式(11)就可得到软母线下料长度LW.

3Matlab仿真与数据比较

以某实际500 kV变电站为例，耐张绝缘子串的链接顺序以右侧耐张绝缘子串为例，至上而下依次为两个U型挂环、球头挂环、绝缘子串、碗头挂环、BN联板、Z型挂板、调整环、耐张串线夹.类似地，左侧耐张绝缘子串只少一个调整环.右侧耐张绝缘子串各个金具与软母线的具体参数信息:绝缘子型号XWP－160，长155 mm，9.2 kg，36支;U型挂环型号U－16，长95 mm，1.5 kg，2支;球头挂环型号QP－16，长60 mm，0.5 kg，1支;碗头挂板WS－16，长95 mm，2.6 kg;Z型挂板型号Z－16，长100 mm，2.4 kg;BN联板BN－16，长100 mm，10.0 kg;调整环型号DT－16，长260 mm，4.2 kg;屏蔽均压环型号PL－1060×600，6.7 kg，耐张串线夹NYZ－1440N，长740 mm，11.6 kg;软导线型号NRLH58GJF－1440/120，截面积1 555.8 mm2，4.942 kg·m－1.将数值计算模型与人工经验方法所得到的下料长度，在软母线安装后，对测量出的总弧垂进行对比，来说明下料长度的准确性.人工经验方法一般为档距减去两侧耐张绝缘子串串长，再加上一个补偿值，其一般调整率为:LW≈L－(λ1+λ2)+ΔL，其中ΔL为人工经验补偿值.为了更加准确地比较两种方法计算出的软母线下料长度的实际安装效果，定义弧垂的相对误差为:δ=(f'0－f0)/f0×100%，式中f0表示设计弧垂，f'0表示装配后实际测量弧垂值.人工经验方法与数值计算模型的数据分别如表1与表2所示.表1表明人工经验方法所获得的δ约为!12%～"13%，需要人工爬杆二次调节调整环;表2表明数值计算模型的δ约为!2%～"3%，无需二次调节，符合变电站软导线弧垂的施工误差范围(!2.5%～"5%).

表1 人工经验方法数据Tab.1Data of artificial empirical method

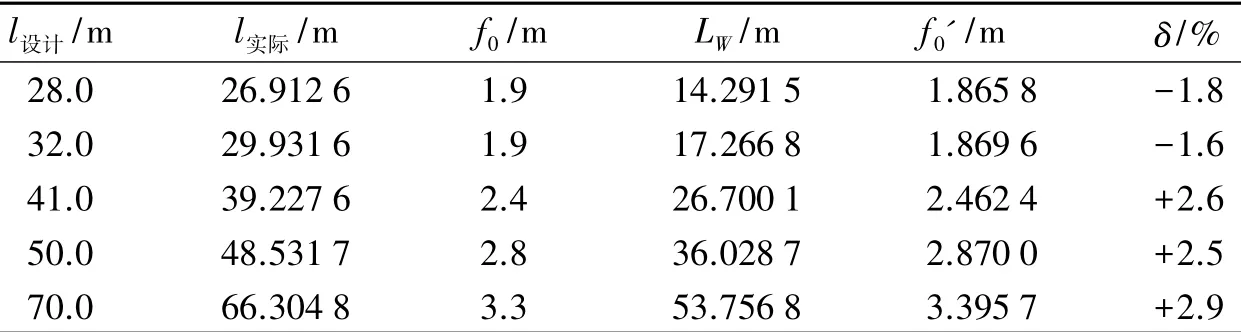
表2 数值计算模型数据Tab.2Data of numerical calculation method

4 结论

建立变电站软母线下料长度数值计算模型，由Matlab仿真验证与多个实际500 kV变电站的工程实践表明，所建立的数值求解模型与传统人工经验方法进行对比，可保证装配后的软母线弧垂误差为!2%～"3%，而人工经验方法误差均大于弧垂国家标准，通常需要调节调整环改进弧垂准确度.

［1］POLEVOY A.Impact of data errors on sag calculation accuracy for overhead transmission line［J］.IEEE Transactions on Power Delivery，2014，29(5):2 040－2 045.

［2］MUHR M，PACK S，JAUFER S.Usage and benefit of all overhead［J］.High Voltage Engineering，2008，34(12):34－35.

［3］张斌，张军，李黎，等.1 000 kV特高压变电站软母线施工放线下料长度计算的探讨［J］.电力系统保护与控制，2008，36(18):81－83.

［4］胡生辉，宋国贵，吴双，等.1 000 kV交流特高压变电站大截面软母线装配长度计算软件的开发研究［J］.湖北电力，2009，33(6):5－7.

［5］成卫，张军，张斌，等.1 000 kV变电站V型串软母线施工中导线下料长度的计算方法［J］.电网技术，2009，33(13): 24－26.

［6］邹广平，孙刚，任方.考虑弯曲刚度影响的跳线长度计算［J］.哈尔滨工程大学学报，2005(4):482－486.

［7］孟遂民.架空输电线路设计［M］.北京:中国三峡出版社，2010:47－68.

(责任编辑:林晓)

The dichotomy numerical calculation model of soft－bus conductor length in transformer substation

HUANG Yanwei，WANG Ting’an
(College of Electrical Engineering and Automation，Fuzhou University，Fuzhou，Fujian 350116，China)

A dichotomy numerical calculation model was proposed to calculate the cutting length for soft－bus conductor in transformer substation.Under the assumption of that the horizontal stress is known，this article establishes a nonlinear coupling analytical model of soft－bus conductor length through stress analysis.Furthermore，it designs a numerical calculation of soft－bus conductor length in transformer substation.Then the numerical calculation obtains accurate numerical solution through dichotomy.It is demonstrated by the result of simulation and application that an accurate soft－bus conductor length can be worked out through the numerical calculation method.Besides，the total sag error of soft wire after installation is between－2%to+3%so that the construction effect will be satisfactory.

transformer substation;soft－bus conductor;cutting length;nonlinear coupling;numerical calculation;dichotomy

TM751

A

10.7631/issn.1000－2243.2016.06.0767

1000－2243(2016)06－0767－07

2015－08－28

黄宴委(1976－)，副教授，主要从事自动检测与控制系统研究，sjtu_huanghao@fzu.edu.cn

福建省自然科学基金资助项目(2015J01245)