二次根式与勾股定理的巧妙结合

江苏省太仓市实验中学八（1）班　季楚悦



二次根式与勾股定理的巧妙结合

江苏省太仓市实验中学八（1）班季楚悦

在学习二次根式和勾股定理结合的计算时，我们学会在网格图中计算出直角三角形、正方形、长方形的面积.对于那些边都在网格线上的图形，我们能够很轻松地求出或看出图形的面积和形状.那么对于那些任意三角形或一些边不与网格的线重合的图形，我们还能那么轻而易举地判断它们的形状、求出面积和边长吗？下面请看一道题目：

题目如图1，在方格纸中的小正方形的面积为1，△ABC的三个顶点都在小正方形的格点上，小刚通过观察得出以下结论：

结论1：△ABC的形状是等腰三角形；

结论3：△ABC的面积为5；

你认为小刚观察的结论正确的有几个？

图1

这个问题看似没有那么简单.可是，如果好好运用勾股定理和二次根式的计算，再结合图形，仔细想一想，问题就迎刃而解啦！

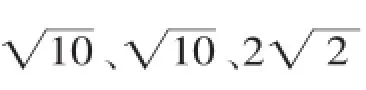
所以，正确的结论有3个.

怎么样？现在是不是恍然大悟了呢？

点评：在初中数学教材中，我们利用“勾股定理”引入平方根概念，利用二次根式的运算，解决了“勾股定理”的综合应用，所以说二次根式与勾股定理是密不可分的.不仅如此，很多几何问题的相关计算都离不开二次根式，二次根式在数学中的地位不可撼动.上述问题体现了数形结合的思想方法，是中考的热点考题.

（指导教师：江美红）