二次根式中的整体思想

江苏省太仓市实验中学八（1）班　蒋诗雨



数学透视眼/数学写作

二次根式中的整体思想

江苏省太仓市实验中学八（1）班蒋诗雨

在平时的实数加减运算和一些其他问题中，整体思想是解题的妙招之一，能将问题简化.其实，在二次根式的运算中，整体思想也同样重要.

有些同学看见这个算式时一定会乱了方寸，用先化简x、y的值，再代入计算的方法来做，当然可以，步骤如下：

化简x、y当然难不倒大家，可是接下来愈发繁琐的计算步骤犹如一个巨大的深坑，有不少同学肯定会掉下去，剩下的也会在其他计算的小石头上摔个跤，能顺利计算出答案到达终点的同学肯定寥寥无几吧.

细心的同学会发现，x、y是一组倒数，那么xy的值就等于1，答案就非常容易出来了，一路平坦直奔终点，步骤如下：

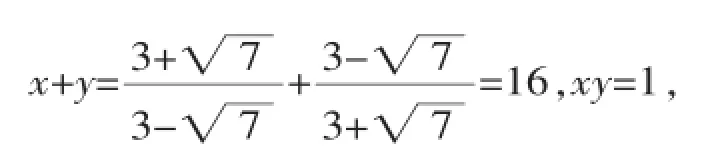
原式=3（x+y）2+4xy=3×162+4=772.

从整体把握x+y与xy，可迅速求值.运用整体思想来做这道题，相对来说，要简便许多.

总之，整体思想解决问题相对来说会减轻同学们做题的负担，在二次根式的学习中也是一种法宝.那么，下面这道例题相信你用整体思想的方法也能很快解决：

祝愿大家有了整体思想这个解题的法宝，在数学路上越走越顺！

点评：二次根式的运算是数学中考的常见考点，整体思想在初中数学中有着广泛的应用，运用整体思想解决二次根式的运算问题，结合乘法公式，巧妙地避开了繁琐的根式运算，整个解答过程思路清晰、简洁明快.二者的结合，集知识和思想于一体，可谓珠联璧合.

（指导教师：江美红）