基于CUDA的并行谱聚类社区挖掘算法*
2016-07-23蒋莉芳苏一丹
蒋莉芳,苏一丹,覃 华
(广西大学计算机与电子信息学院,广西 南宁 530004)
基于CUDA的并行谱聚类社区挖掘算法*
蒋莉芳,苏一丹,覃华
(广西大学计算机与电子信息学院,广西 南宁 530004)
摘要:社会网络和社交媒体数据具有大规模、高维度的特性,社区挖掘算法的计算效率是一个值得研究的问题。针对此问题,本文利用CUDA并行计算架构,提出一种并行的谱聚类社区挖掘算法,首先对高维的社会网络数据集进行降维,再用CUDA的并行计算能力提高谱聚类算法的计算效率。实验表明,本文所提算法能有效地提高社区挖掘算法的计算速度,并行计算效率较常规算法有5~8倍的提高,为社区挖掘计算提出一种新的思路。
关键词:社区挖掘;CUDA;并行计算;谱聚类;大规模网络
1概述
快速增长的社交媒体,形成了很多规模巨大和维数众多的网络,社区发现成为了理解网络拓扑结构的重要技术[1,2]。
目前的社区发现算法中,大多数算法的性能其实都很优越,如Luxburg提出的谱聚类算法(Spectral Clustering,SC)[3],通过求解图分割问题获得网络划分。Newman提出了Modularity算法[4],考虑节点度的分布情况,用两点间的实际作用和期望值之差,定义社区效应强度,通过最大化效应强度,获得最佳的社区划分。再比如郭进时等[5]提出的联合拓扑与属性的社区模糊划分算法,用完全相异距离指数将拓扑结构与属性相结合,以此作为隶属关系建立模糊等价关系矩阵,再选择合适的聚类对网络进行社区划分。这些算法都能在一定程度上达到社区发现的效果,但这些算法的计算量都很大。在大数据时代,网络社区规模越来越大,时间复杂性的弊端,也就显得尤为突出,特别是还要进行多维处理时,因此需要进一步改进。并行和分布式计算是降低总体运行时间的有效途径,已经有学者在Mapreduce上面进行网络结构的探索,但是总体而言,社区发现的并行计算研究文献还较少[6,11,12]。本文研究的主要目标是利用并行计算的思想,解决社区挖掘算法中的时间需求过大问题。
CUDA(Compute Unified Device Architecture)是NVidia公司设计开发的一种在GPU上进行通用、并行计算的编程体系结构[7,8]。本文利用CUDA平台实现对多维数据集的并行谱聚类算法(Multi-Dimension Spectral Clustering,SpectralDim),并用于社区挖掘算法。谱聚类算法对于社区网络数据的高维问题,采用拉普拉斯特征向量方式进行降维,最后再用聚类算法进行社区挖掘。其本身自带的降维功能,使得其自身时间复杂度比其他社区挖掘算法低。本文利用CUDA并行谱聚类算法挖掘社区信息,提高了挖掘算法对大规模社区数据的适用能力。本文实验使用文献[9]的数据,并将SpectralDim_CPU(不用并行)、SpectralDim_GPU(CUDA并行)与文献[9]中的SocioDim比较,实验结果表明:本文所提算法的计算准确率与SocioDim相当,但是计算速度较SocioDim算法快5~8倍,更适合于大规模社区挖掘。
2基于谱聚类的社区发现算法
谱聚类算法利用谱分析技术可将高维数据投射到低维子空间,达到降维的效果。而当数据拥有多维(Multi-Dimension)特征时,需要先对数据进行效用集成才能进行谱聚类,文献[8]采用平均效用法进行数据集成,并采用谱分析技术对数据进行降维,最后用SVM对降维后的数据进行社区划分。
从降维和图分割理论对谱聚类进行理解,规范化拉普拉斯聚类算法的目标函数为:
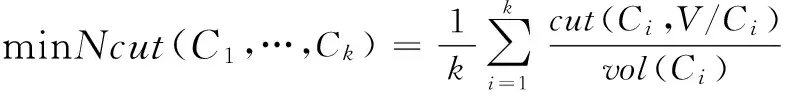
(1)

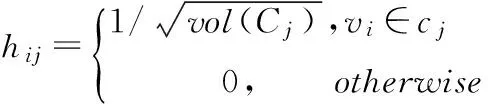
(2)
则目标函数可转换为如下迹函数的求解:
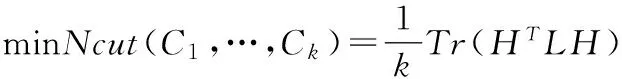
(3)
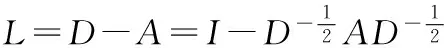
一般的谱聚类算法流程如下所示:

输入:原数据集,聚类数目k1、求矩阵的相似性矩阵A以及度矩阵D2、计算拉普拉斯矩阵L=D-A3、求取L的前k个最小特征向量4、对特征向量进行聚类得到C输出:聚类结果C
如若数据集有多模特征,则在相似度矩阵的计算过程中,采用效用集成或者网络集成的方式进行维度集成,再计算相似度。
3基于CUDA的并行社区挖掘算法
接下来对本文中运用到的谱聚类CUDA化的关键技术以及并行化过程中所涉及的地方进行讨论。分析谱聚类的算法流程可知,可进行并行化分析的是1、3、4步骤,其中第一步属于矩阵计算,第三步涉及特征值求解的计算,第四步涉及K-means聚类的计算。从后面实验部分三个核函数的运算时间对比可知,这三个部分占了算法总体运行时间的大部分,且特征值求解过程是最费时间的,具体的并行过程下面一一述之:
3.1矩阵的并行计算
数据挖掘算法多半涉及大量的矩阵操作,社区挖掘也不例外。本文使用cuBLAS程序库实现矩阵的并行计算操作,采用CUSP支持库实现对稀疏矩阵的并行计算。cuBLAS利用GPU加速向量、矩阵的线性运算,比如说cublasSgemm用来处理单精度矩阵,也就是float型的乘法运算。cublasSasum()用来实现矩阵的加法运算。比如说拉普拉斯矩阵的计算过程中,即是用cublasSasum()函数求得。
3.2特征值求解的并行计算
在对拉普拉斯矩阵进行特征值分解的过程中,由于矩阵是对称半正定的,故本文用Lanczos法将对称矩阵通过正交相似变换成三对角矩阵 ,即:

则L的特征值和特征向量,可通过T求解出[10]。再通过QR方法求解出T的特征值和特征向量[13]。因此,本文用Lanczos和QR相结合的办法求取矩阵的特征值,Lanczos-QR法的算法流程如下:

输入:拉普拉斯矩阵L单位向量;v1(n*m),v0=0,β1=01、For=1,2,…,m wj=Lvj-βjvj-1 αj=
从算法流程可知,上述算法主要也是由矩阵运算组成。而拉普拉斯矩阵在大规模的数据集中,也是有稀疏性的,因此Lanczos-QR算法的并行计算也主要通过cuBLAS和CUSP组合实现。
4实验
4.1实验环境和实验数据
本文的PC机硬件为:CPU,Intel Pentium G640(双核),主频2.80 GHz,内存2 GB;nVIDIA显卡,GeForce GT730,1 GB显存。软件环境为:Windows XP sp3,Visual C++ 2010,CUDA 6.5。
测试数据集取自文献[8]的BlogCatalog社交网站数据,数据集的相关参数。BlogCatalog数据集采集了10 312个用户在39个博文分类目录下的交互,如转发等,每个用户平均发布1.6个类别的博文。
4.2算法效率对比
本文分别实现了串行和并行的社区发现算法,用于进行并行算法的性能对比。本文共实现了三个核函数:Laplace_CU<<
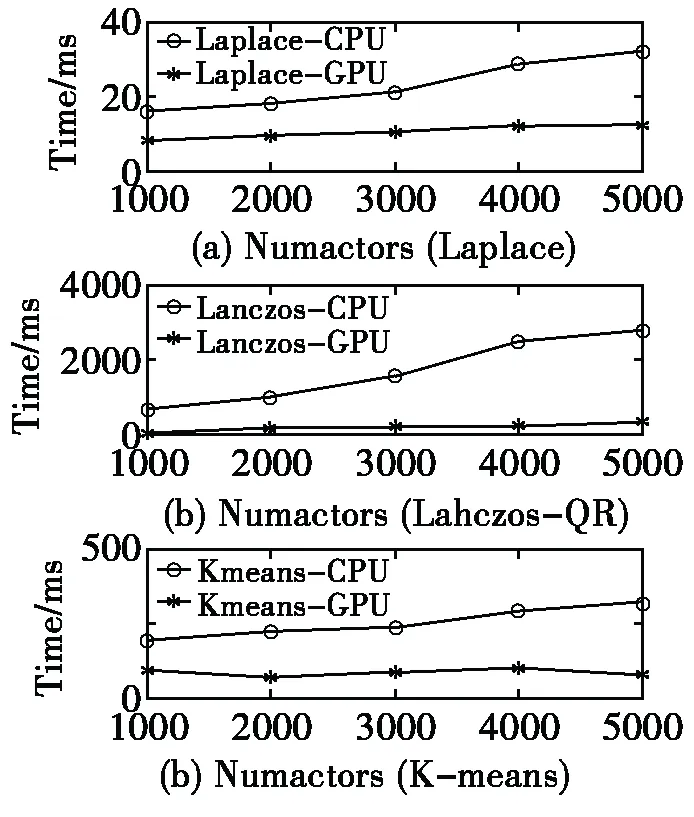
图1 BlogCatalog上各部分运行时间随数据集大小的变化
从图1中可以看出,总体而言本文提出的并行算法的各部分执行时间都有明显的减少。随着数据集的变大Lanczos_QR求取特征值的计算可以得到3-10倍的加速,而Laplace的求取和K_means的计算过程中,时间变化并不大,但是CUDA并行基本上也有2倍左右的加速。
不过K_means在并行的过程中,由于受到聚类个数K值和迭代次数的影响,运行时间不太稳定。本文的下一步工作之一就是探索迭代算法中迭代次数可由程序改变的时候,并行迭代算法的网格和线程设计,以及并行迭代算法的衡量。
对比图1的纵轴,发现Lanczos_QR和K_means占了整个算法运行时间的85%以上,也就是说特征向量的并行化和聚类的并行化是整个算法改进的重点,探索特征向量求取更快速的算法和更深程度的并行化是我们下一步研究内容。
上述三部分的时间比较,已经考虑了各步骤中CPU和GPU的通信时间,整个算法的时间加速比如下图所示。
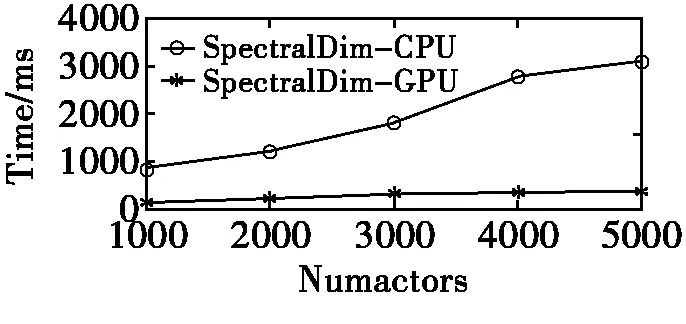
图2 SpectralDim随数据集变化的运行时间
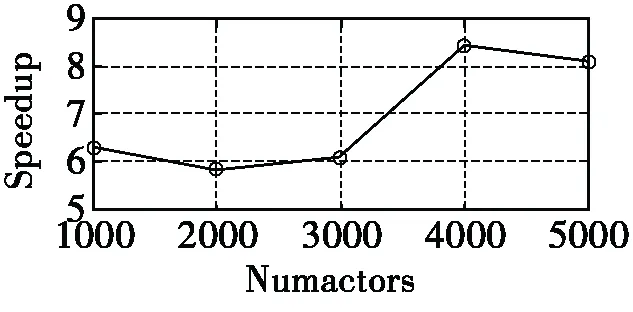
图3 SpectralDim的加速比变化
可以看到随着数据集大小变大,GPU上面的运行时间基本上没有发生变化,从图3可以看出整个算法的加速比在6~8之间。
实验1是对本文算法内部的纵向比较,为了了解本文算法的整体性能,笔者进行了实验2。实验2用整个BlogCatalog数据集分别测试本文算法_CPU、本文算法_GPU、SocioDim算法的运行时间和算法性能。
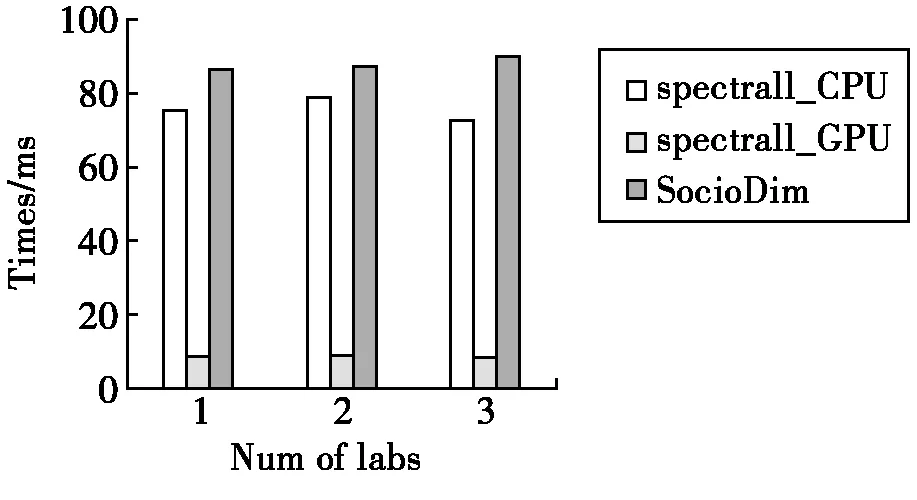
图4 算法运算时间比
图4表明,SpectralDim_GPU的运算速度比其余两者都高,而SocioDim的运算速度比SpectralDim_CPU略高。由于两者的差别只在于最后聚类部分,本文采用K_means算法,而SocioDim采用LIBSVM。这个表现和K_means和SVM的时间复杂度不太相符,本文猜测是SVM中强制定义了迭代次数,而本文的K_means是寻找最优聚类而导致的。
为了衡量算法的社区发现效果,本文采用F1、accuracy来衡量算法性能。
下图表示随着训练集百分比(训练集占整个数据集的百分比)的增加,算法性能的变化。
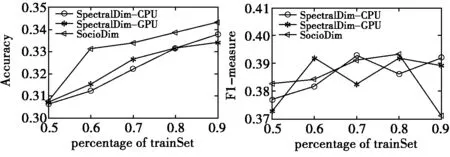
图5 Accuracy对比 图6 F1-measure对比
从图中可以看出,随着训练集所占比重的增加,三种算法的准确率也随着增加。不过总体上SocioDim的accuracy略高于本文所设计的算法,但是F1的变化和训练集比重关系不大,三种算法的F1均有高有低。
总的来说,通过实验1和实验2,我们可以得出这样的结论:基于CUDA平台设计的并行SpectralDim算法,能有效处理高维数据,在社区发现准确性的前提下,能有效提高运行速度,一定程度上能解决社区发现算法受制于大规模数据集的问题。
5结束语
本文在CUDA架构下设计并实现了并行社区发现算。实验表明,本文算法保证准确性的前提下,能有效提高运算速度,可加速5~8倍左右,提高了社区挖掘算法处理大规模数据集的能力,但后续工作仍需要处理内存占用率等。
参考文献
[1]Wu F,Huberman B A.Finding Communities in Linear Time:A Physics Approach[J].The European Physical Journal B-Condensed Matter and Complex Systems,2004,38(2):331-338.
[2]Newman M E J,Girvan M.Finding and Evaluating Community Structure in Networks[J].Physical Review E,2004,69(2):026113.
[3]Von Luxburg U.A Tutorial on Spectral Clustering[J].Statistics and Computing,2007,17(4):395-416.
[4]Newman M E J.Finding Community Structure in Networks Using the Eigenvectors of Matrices[J].Physical Review E,2006,74(3):036104.
[5]郭进时,汤红波,葛国栋.一种联合拓扑与属性的社区模糊划分算法[J].计算机工程,2013(11):35-40.
[6]Seunghyeon Moon,Jae-Gil Lee,Minseo Kang.Scalable Community Detection From Networks by Computing Edge Betweenness on MapReduce[C]//Big Data and Smart Computing (BIGCOMP),2014 International Conference on,vol.,no.,145,148,15-17 Jan. 2014.
[7]Garland M,Le Grand S,Nickolls J,et al.Parallel Computing Experiences with CUDA[J].IEEE Micro,2008(4):13-27.
[8]Kirk D.NVIDIACUDA Software and GPU Parallel Computing Architecture[C]//ISMM,2007,7:103-104.
[9]Tang L,Liu H.Leveraging Social Media Networks for classification[J].Data Mining and Knowledge Discovery,2011,23(3):447-478.
[10]Matam K K,Kothapalli K.GPU Accelerated Lanczos Algorithm with Applications[C]// Advanced Information Networking and Applications (WAINA),2011 IEEE Workshops of International Conference on , vol., no., pp.71,76, 22-25 March 2011.
[11]Varamesh A,Akbari M K,Fereiduni M,et al.Distributed Clique Percolation Based Community Detection on Social Networks Using MapReduce,[C]// Information and Knowledge Technology (IKT), 2013 5th Conference on , vol., no., pp.478,483, 28-30 May 2013.
[12]Lunagariya D C,Somayajulu D V L N,Krishna P R.SE-CDA:A Scalable and Efficient Community Detection Algorithm[C]//ta (Big Data), 2014 IEEE International Conference on , vol., no., pp.877,882, 27-30 Oct. 2014.
[13]Zhou K X,Roumeliotis S.A Sparsity-aware QR Decomposition Algorithm for Efficient Cooperative Localization[C]//Robotics and Automation (ICRA),2012 IEEE International Conference on. IEEE, 2012:799-806.
收稿日期:2015-12-07
基金项目:国家自然科学基金(61363027)
作者简介:蒋莉芳(1991- ),女,硕士研究生,主研方向:数据挖掘、舆情分析。
文章编号:1674- 4578(2016)02- 0046- 04
中图分类号:TP311.13
文献标识码:A
Parallel Spectral-cluster Algorithm for Social Community Mining Based on CUDA
Jiang Lifang, Su Yidan, Qin Hua
(SchoolofComputerandElectronicInformation,GuangxiUniversity,NanningGuangxi530004,China)
Abstract:It is a problem for computing efficiency when mining towards social networks and social media because of the feature of magnitude and high-dimensionality. To solve this problem, the paper uses CUDA parallel architecture to propose a parallel spectral-cluster algorithm for community-mining. It firstly reduces the high-dimensional social network data sets and then improves the efficiency of spectral-cluster algorithm with parallel computing capabilities of CUDA. The experiments show that the algorithm can do effective improvement to the speed of community-discovering and has an increase of 5~8 times for the efficiency of parallel computing compared with conventional algorithm, it presents a new thinking for community-mining computing.
Key words:community mining; CUDA; parallel computing; spectral-cluster; large-scale data
