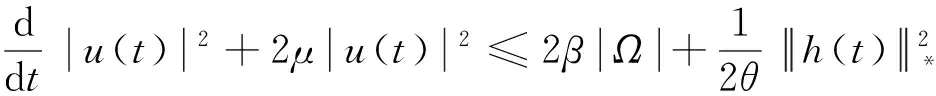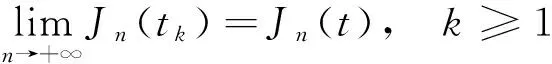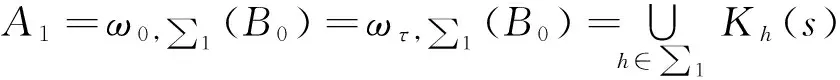非局部扩散的非自治抛物方程动力学行为

常伟伟,李晓军

(河海大学 理学院，江苏 南京 210098)



非局部扩散的非自治抛物方程动力学行为

常伟伟,李晓军

(河海大学 理学院，江苏 南京 210098)

摘要：考虑带非局部扩散的非自治抛物方程解的长时间行为,当时间符号项于(�；H-1(Ω))和(�;L2(Ω))中平移有界时,证明该系统所对应的过程在L2(Ω)与(Ω)中存在一致吸引子。

关键词：一致吸引子；非局部扩散；非自治抛物方程

0引言

(1)

其中：Ω⊂N为有界开集；a∈C(,+)为局部Lipschitz连续函数，满足

0

(2)

其中：m,M为正常数。l∈(L2(Ω))′,f∈C()且存在常数η>0,cf≥0满足

(3)

(f(s)-f(r))(s-r)≤η(s-r)2,∀s,r∈。

(4)

1预备知识

首先给出解的定义及其有关结果。

(5)

由式(2)、式(3)及定义1可知：方程(1)的弱解满足u′∈L2(τ,T;H-1(Ω))。因此，由文献[12]中的定理7.2可知：u∈C([τ,T];L2(Ω))。进一步，对任意的τ≤s≤t,方程(1)的弱解满足能量等式：

(6)

(7)

下面给出方程(1)的适定性,证明见文献[7]。

定理1假设a是局部Lipschitz连续且满足式(2)，f∈C()满足式(3)和式(4)，l∈(L2(Ω))′。如果(;H-1(Ω))，则对任意uτ∈L2(Ω)，方程(1)有唯一弱解u(t)存在，且连续地依赖于初值。进一步如果(;L2(Ω))，则对∀ε>0,T>τ+ε，弱解u满足u∈C((τ,T)。若，则且u是强解。

考虑下面抽象非自治发展方程：

∂tu=Aσ(t)(u),t∈。

(8)

对任意的s∈,由方程(8)给定一发展算子Aσ(s)(.):E1→E0，其中，E1,E0是Banach空间，函数参数是σ(s),s∈，表示方程依赖于时间，称为时间符号。σ(s)的函数值属于某一度量空间或Banach空间Ξ，也就是说，对任意的(或a.e.)s∈,σs∈Ξ。

给定方程(8)的初值：

(9)

其中：E是一个Banach空间，满足E1⊆E⊆E0。假设对任意的符号σs∈∑，∑⊂Ξ是一个参数集，方程(8)和式(9)对任意的τ∈和uτ∈E是唯一可解的。因此，方程(8)和式(9)的解可以用双参数算子来表示：

u(t)=Uσ(t,τ)uτ,uτ∈E,∀t≥τ,t,τ∈,σ=σ(s)∈∑。

定义3定义于Banach空间E上的双参数映射族{Uσ(t,τ),t≥τ,τ∈},σ∈∑，称为关于符号σ∈∑的一族过程，如果对任意的σ∈∑，

Uσ(t,τ):E→E,t≥τ,τ∈,

满足下面的多重特性：

(Ⅰ)Uσ(t,s)Uσ(s,τ)=Uσ(t,τ),∀τ≤s≤t,τ∈。

(Ⅱ)Uσ(τ,τ)=Id是恒等算子,τ∈。

由方程(8)和式(9)的唯一可解性知，下面的平移等同性有效：

Uσ(t+h,τ+h)=UT(h)σ(t,τ), ∀σ∈∑,t≥τ,τ∈,h≥0,

定义4集合B0⊂E称为过程{Uσ(t,τ)}，σ∈∑的一致吸收集，如果对任意的τ∈，B∈B(X)，都存在t0=t0(τ,B)≥τ，则下式成立：

定义5集合A∑是过程{Uσ(t,τ)}，σ∈∑的一致(w.r.t.σ∈∑)吸引子，如果A∑是一致(w.r.t.σ∈∑)吸引Ε中的任何有界集(一致吸引特性)，且包含于任何一个闭的一致吸引集A′中，即A∑⊆A′(最小特性)。

本文将用到下面的抽象结果：

定理2[13]令∑是一Banach空间的子集，且在平移半群T(t)下是连续不变的(T(t)∑=∑)，并满足平移等同性。一族过程{Uσ(t,τ)}，σ∈∑，拥有一个紧的一致(w.r.t.σ∈∑)吸引子A∑满足

A∑=ω0,∑(B0)=ωτ,∑(B0),∀τ∈，

当且仅当{Uσ(t,τ)}，σ∈∑，满足：

(Ⅰ)有一个有界的一致(w.r.t.σ∈∑)吸收集B0。

(Ⅱ)是一致(w.r.t.σ∈∑)ω-极限紧的。

另外，若∑是Ξ中的弱紧集，{Uσ(t,τ)}是弱连续的，且满足条件(Ⅰ)和条件(Ⅱ),则A∑满足：

其中：∑0为∑的弱闭包；Kσ(0)为在t=0时核Kσ的截片。

2主要结果

(10)

(11)

引理1假设f满足式(3)、式(4)和式(10)，且h∈∑，那么方程(1)所生成的过程族{Uh(t,τ)}，h∈∑在L2(Ω)存在一致(w.r.t.h∈∑)吸收集B0。

证明方程(1)的两边与u作内积得：

由Cauchy-Schwarz不等式、式(3)和式(10)可得：

(12)

故由Young不等式可得：

(13)

应用Poincare不等式和式(13)可得：

其中：0<θ

(14)

引理2在引理1的假设下，方程(1)所生成的过程族{Uh(t,τ)}，h∈∑在L2(Ω)是一致(w.r.t.h∈∑)ω-极限紧的。

(15)

由式(15)知：u∈C([τ,T];L2(Ω)),且u在(τ,T)上满足等式(5)。

un在C([τ,T];H-1(Ω))中强收敛到u。

(16)

un(sn)在L2(Ω)中弱收敛于u(s*)。

(17)

如果证明

un在C([τ,T];L2(Ω))中强收敛到u，

(18)

由此，可得到{un(tn,τ,fn,uτn)}在L2(Ω)是相对紧。假设存在ε>0及序列{tn}⊂[τ,T]，不失一般性，设tn收敛到t*，有：

(19)

由式(18)推出：

(20)

另一方面，应用能量等式(6)、Young不等式、式(2)和式(10)得：

其中：z代表u或un。定义下面函数：

由u和un的正则性，Jn和J在[τ,T]上是连续非增函数，可得：

Jn(s)→J(s),∀s∈[τ,T]。

故存在{tk}⊂[τ,T]满足tk→t*，当k→+∞时，有：

对ε>0，存在k(ε)≥1，由J在[τ,T]上的连续性知：

Jn(tn)-J(t*)≤Jn(tk(ε))-J(t*)≤

ε,∀n≥nε。

(21)

由定理1可知：

引理3在引理1的假设下，方程(1)所生成的过程族{Uh(t,τ)}，h∈∑在L2(Ω)上连续。

由引理1～引理3，应用定理2，有以下主要结果：

定理3假设f满足式(3)、式(4)和式(10)，则由式(1)产生的过程族{Uh(t,τ)}，h∈∑在L2(Ω)有一致(w.r.t.h∈∑)吸引子A，A在L2(Ω)中是紧的，且吸收L2(Ω)中的所有有界集。进而

其中：B0为L2(Ω)的一致(w.r.t.h∈∑)吸收集；Kh(s)为在t=s时核Kh的截片。

证明方程(1)两边用-△u于L2(Ω)中作内积，可得:

(22)

应用式(2)、式(3)和Poincare不等式，由式(22)可得：

(23)

由引理1可知，过程{Uh(t,τ)}于L2(Ω)中存在一致吸收集B0，故存在T=T(B0)，由式(13)可得：

(24)

3结束语

参考文献：

[1]ZHENGSM,CHIPOTM.Asymptoticbehaviorofsolutionstononlinearparabolicequationswithnonlocalterms[J].Asymptoticanalysis,2005,45(3):301-312.

[2]MENEZESDSB.Remarksonweaksolutionsforanonlocalparabolicproblem[J].Internationaljournalofmathematicsandmathematicalsciences,2006,2006:1-10.

[3]CHIPOTM,LOVATB.Ontheasymptoticbehaviourofsomeproblems[J].Positivity,1999,3(1):65-81.

[4]ANGUIANOM,KLOEDENPE,LORENZT.Asymptoticbehaviourofnonlocalreactiondiffusionequations[J].Nonlinearanalysis,2010,73:3044-3057.

[5]ANDAMIOA.Asymptoticbehaviorfordiffusiongovernedbynonlocalinteraction[J].Electronicjournalofdifferentialequations,2010,17(1):1555-1666.

[6]CHIPOTM,MOLINETL.Asymptoticbehaviourofsomenonlocaldiffusionproblems[J].Applicableanalysis,2001,80(3/4):279-315.

[7]CARABALLOT,HERRERA-COBOSM,MARIN-RUBIOP.Longtimebehaviorofanonautonomousparabolicequationwithnonlocaldiffusionandsublinearterms[J].Nonlinearanalysis,2015,121:3-18.

[8]GARCIA-LUENGOJ,MARIN-RUBIOP.Reaction-diffusionequationswithnon-autonomousforceinH-1anddelaysundermeasurabilityconditionsonthedrivingdelayterm[J].Journalofmathematicalanalysisandapplications,2014,417(1):80-95.

[9]胡妤涵.具有Neumann边界的耦合非线性薛定谔方程组能量估计[J].河南科技大学学报(自然科学版),2016,37(1):96-100.

[10]高娟娟,贾小尧,马继佳.一类p(x)-Laplacian问题解的存在性[J].河南科技大学学报(自然科学版),2014,35(3):86-89.

[11]CHEPYZHOVVV,VISHIKMI.Attractorsforequationsofmathematicalphysics[M].RhodeIsland:AmericanMathematicalSociety,2002.

[12]ROBINSONJC.Infinite-dimensionalsystemsanintroductiontodissipativeparabolicPDEsandthetheoryofglobalattractors[M].Cambridge:CambridgeUniversityPress,2001.

[13]LUSS,WUHQ,ZHONGCK.Attractorsfornonautonomous2Dnavier-stokesequationswithnormalexternalforces[J].Discreteandcontinuousdynamicalsystems,2005,13(3):701-709.

基金项目：国家自然科学基金项目(11571092)

作者简介：常伟伟(1990-)，女，河南南阳人，硕士生；李晓军(1970-)，男，甘肃定西人，副教授，博士，硕士生导师，主要研究方向为非线性泛函分析.

收稿日期：2016-01-04

文章编号：1672-6871(2016)05-0077-06

DOI:10.15926/j.cnki.issn1672-6871.2016.05.017

中图分类号：O175

文献标志码：A