逆向几何求交方法的STL模型分层算法

段明德，郑立霞，李明利，张壮雅

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.洛阳LYC轴承有限公司，河南 洛阳 471003)



逆向几何求交方法的STL模型分层算法

段明德1，郑立霞1，李明利2，张壮雅1

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.洛阳LYC轴承有限公司，河南 洛阳 471003)

摘要：为了解决三维网格曲面(STL)模型分层算法分层计算效率不高的问题，提出了一种可实现STL曲面模型快速分层的逆向几何求交算法。通过遍历三角面片顶点坐标，确定模型最小包围盒。利用分层面分割STL模型，散列表数据结构记录分层面坐标。在此基础上，计算连接截交线，生成模型轮廓，实现模型的快速分层。实验结果证明：该算法可对各种结构的STL模型进行分层，具有可靠、稳定和效率高等优点。

关键词：几何求交；三角网格；STL模型；快速分层

0引言

随着制造业的迅速发展，快速成型作为新兴技术越来越受到重视。高效准确地得到网格模型是分层制造的关键[1]，因此，分层问题一直是三维网格曲面(stereolithogrphy interface,STL)模型分层算法研究中的热点。文献[2]对三角网格和四面体的体素化算法做了研究。文献[3]在对STL模型进行分层计算时，将三角面片的顺序关系融于交点链表中，以节省系统资源和提高计算效率。文献[4]基于数学形态学运算和拓扑规则消除网格中的拓扑缺陷，有效地提高了网格质量。文献[5]基于测地距离和图割法对网格进行分割，具有一定的适用性。文献[6]对三角网格现有的分割算法进行了综合性的总结。文献[7]改善了三角网格中的半径顶点，而不改变之间的联系，提高了建模精度，改善了3D打印产品的质量。文献[8]对任意三角网格表面线段的连续性和可见性进行了研究，并通过分配所有正交点和三角网格表面单元提高了计算效率。STL模型等厚分层算法最常见的有基于模型毗邻关系的分层算法和基于三角面片几何特征的分层算法。当前者出现分层面与三角面片的公共点相交时，将无法确定下一个待分层三角面片，造成在计算过程中的算法失败而无法进行计算。后者在分层时虽然省去了不相交三角面片的计算，但是这种算法仍然没有明确的划分标准，分层面与三角面片位置关系的无效判断依然不可避免。

综上所述，在对STL模型进行分层方面，还存在着分层繁琐的问题。本文针对此问题进行了研究，在分层计算时，采用几何求交逆向算法，除去不相交三角面片，处理顶点与分层面相近的三角面片。通过相交三角面片搜寻与之存在交点的分层面求取截交线，并运用实例验证了此方法的可行性与有效性，可为快速成型分层制造提供理论依据和技术支持。

1算法描述

为了解决STL模型在分层时出现的效率不高和算法失效等问题，本文提出了基于三角面片几何特征逆向算法，在读取STL模型过程中，建立模型最小包围盒，确定分层范围，选择Z向为分层方向进行讨论。模型分层示意图见图1。如图1所示，矩形DEFG为包围盒平行Z向的截面图形，在分层过程中，首先设置分层厚度t，记录所有分层面，除去与相应分层面不存在相交的三角面片，如图1中的分层面s1除了与三角面片a1、a4和a5相交之外，与三角面片a2和a3并不相交，在进行s1的计算时，除去三角面片a2和a3。然后统一用相交三角面片搜寻与其相交的分层面，计算截交线段，并处理错误轮廓信息，如图1中分层面s2与三角面片a1、a2、a3、a4和a5的顶点均相交的情况，处理结果只有一个交点。最后连接截交线段，生成截面封闭轮廓线，为了提高搜索分层面和计算截交线效率，用散列表的数据形式表达分层面，Z向的各封闭轮廓即实现了STL模型的分层。图2为分层模型截面示意图，其中：s1,s2,s3,…,si对应的截面分别为f1,f2,f3,…,fi。其他方向的分层亦如此。

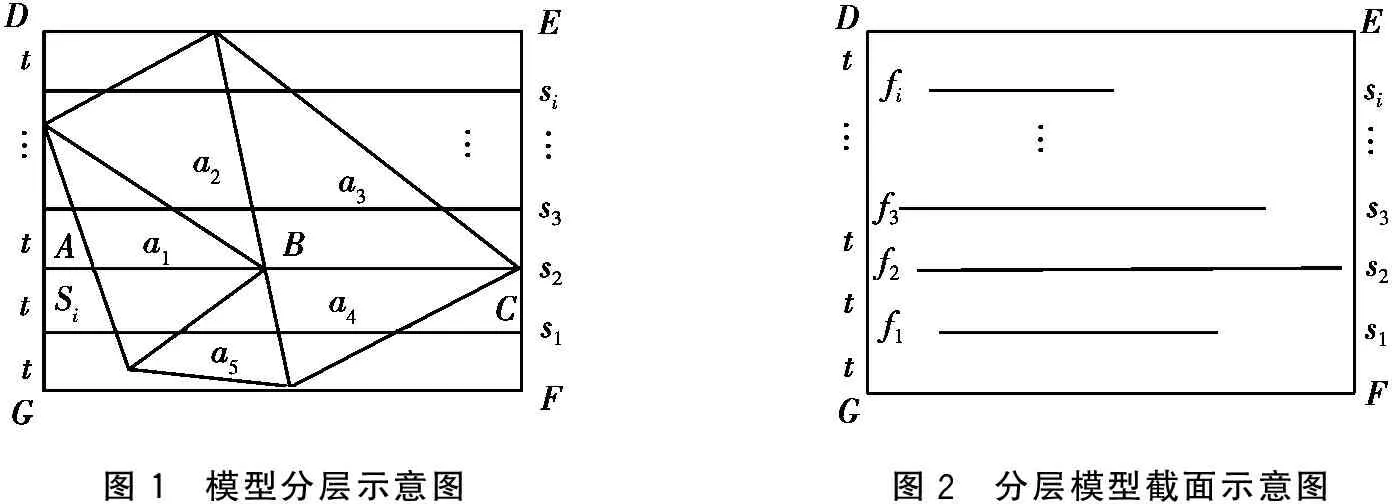
图1 模型分层示意图图2 分层模型截面示意图

2算法实现

2.1求取分层面

在获得分层面之前，首先确定分层的范围，即模型的最小包围盒。在读取STL模型时，可得到模型的Z向最大值max{Z}和最小值min{Z}，以及模型的最大边界点(xmax,ymax,zmax)和最小边界点(xmin,ymin,zmin)。根据模型的最大边界点和最小边界点建立模型的最小包围盒，即模型的分层范围。给定分层厚度t，对STL模型从min{Z}开始进行分层，直至max{Z}结束，分层面的计算如式(1)所示。将散列表用V表示，V中各分层面对应的坐标根据式(2)确定。

z=si，(i=0,1,2,…,n)；

(1)

(2)

其中：si为第i个分层面对应的分层面坐标值；t为分层厚度；i为第i个分层面对应的序列值；max{Z}和min{Z}分别为Z向坐标的最大值和最小值。

图3　散列表结构示意图

分层过程中，每一次分层就有一组分层结果与分层面对应，所以，为了方便后续计算，需要给V中的每一项加上一个指针Si，指针指向分层结果存储的区域，即指针Si指向si的分层结果，则可以将式(2)用图3所示的散列表结构形式表示。

2.2三角面片分层处理

在对STL模型分层时，在STL模型最小包围盒内，顶点Z向坐标值最小 (min{Z})的三角面片先被分割，顶点Z向坐标值最大(max{Z})的三角面片最后被分割。而当三角形顶点Z向坐标值的最大值小于分层面的Z向坐标值或者顶点Z向坐标值的最小值大于分层面的Z向坐标值，三角面片与该分层面均无相交，在后续计算截交线时先把不与分层面存在交点的三角面片除去，提高程序计算的效率。为了除去不与分层面相交的三角面片，针对分层后的三角面片进行两次整合排序[9]。该处理不仅减少了对不相交三角面片的计算与判断，而且还提高了计算效率，节省了对三角面片的存储空间。

2.3逆向几何求交计算截交线段

处理后的三角面片与相应的分层面求取截交线段，为后续连接截交线段作准备。采用逆向几何求交算法计算截交线段，在包围盒中按照一定顺序依次选取三角面片；然后在V中查找与其相交的分层面；最后计算三角面片与分层面交点，得到每一层的截交线段。因此，如何在V中查找到与三角面片存在交点的分层面是计算的关键。

首先寻找分层面，主要是在V中寻找对应的si的值，si与分层面一一对应，因此只要确定si的值即可确定相应分层面。此外，si与i一一对应，确定了i即可得到对应的si的分层序列值。假设第m个三角面片与分层面si相交，由图2可知，三角面片am与分层面si相交的条件为：

(3)

将式(2)和式(3)联立解得：

(4)

(5)

2.4修正错误轮廓信息

计算截交线过程中，会出现分层面与三角面片的顶点相距非常近的情况，利用式(5)进行求解截交线时，会造成截交线计算误差过大或者算法失效等问题。为提高算法健壮性，本文对三角面片的顶点接近分层面的3种情况进行了分析与修正。图4为三角面片的顶点接近分层面示意图。

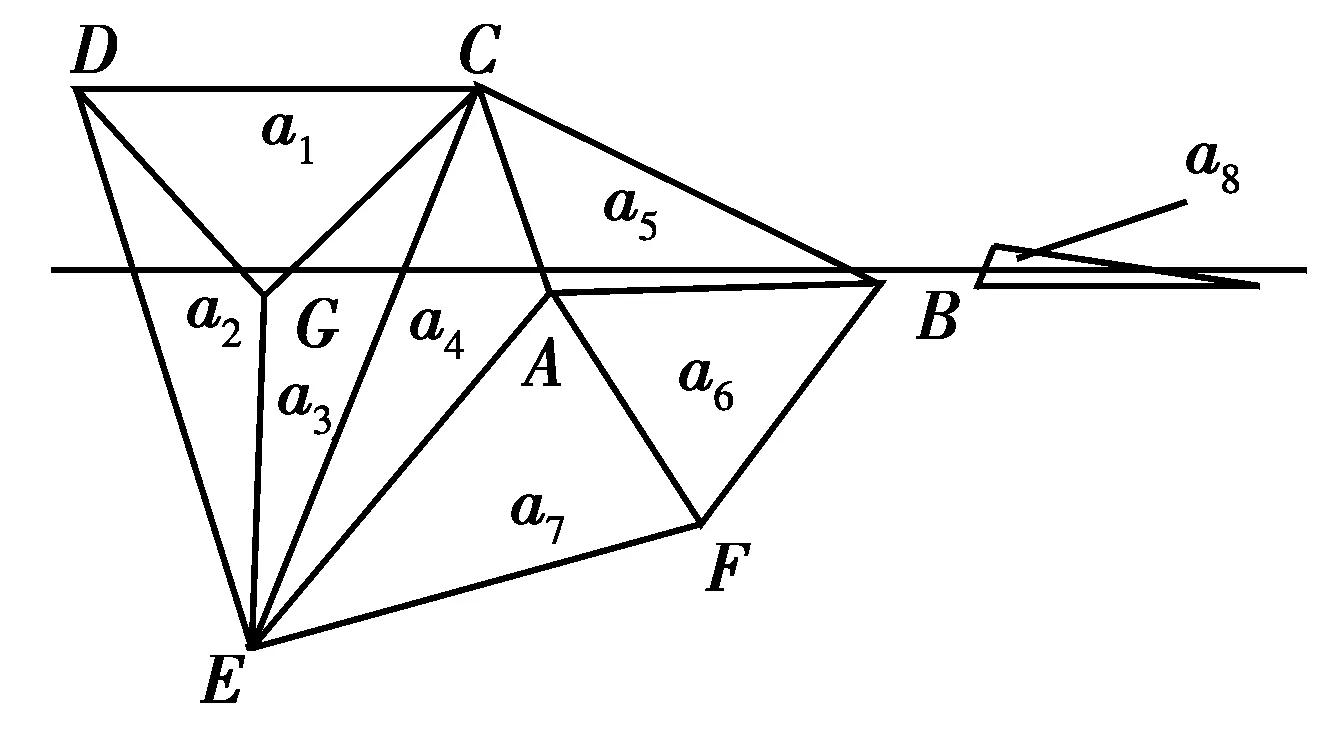
图4　三角面片的顶点接近分层面示意图

(Ⅰ)三角面片3个顶点有1个接近分层面，如图4所示。当计算三角面片a1与分层面si的截交线时，由于点距离分层面太近，会造成截交线求解失败或误差过大，但是截交线过于短小，甚至小到可以认为顶点在分层面上的时候。此时的截交线因过小可以忽略不计，对最终截交线的封闭性和连接几乎没有影响。

(Ⅱ)三角面片中有2个顶点接近分层面，如图4中顶点A和B距离分层面都很近，在计算分层面与三角面片a6的交点时可能出现2个交点或者1个交点，甚至没有交点。但事实上，分层面与三角面片a6是没有交线的，在计算截交线时会出现误差。同理，与三角面片a6共AB边的三角面片a5或许会出现类似的情况。在计算截交线的过程中可能会导致出现重边和缺边两种错误。在同一分层中，若出现多个分层面与三角面片相交的这两种情况，将会在后续的轮廓线连接中出现错误。

针对这两种错误，采取近似平行边判定方法来解决。比较三角面片任一条边上两顶点Z坐标的差值△z，如果小于给定的值θ1，并且两顶点所在边与分层面的夹角(用边的斜率|k|确定)小于给定值θ2，那么，就认为是近似平行边。否则，确定与此边最近距离的分层面，并计算截交线。θ1取值为0<θ1≤1/2t，t为分层厚度，k的范围是0<|k|≤1,可依据经验选取k=0.4，此时的三角面片中该边与分层面的夹角大约为22°。

近似平行边与最近距离的分层面层号的确定：假设三角面片中该边两顶点的Z向坐标分别为z1和z2，如果maxZ-si<θ3(0<θ3≤1/2t)成立，那么si为最近分层面；反之，若maxZ-si>t-θ3成立，则i进行i++运算，此时si+1为最近的分层面。

(Ⅲ)当三角面片的形状为细小狭长的三角形，且3个顶点都比较接近分层面时，如图4中的三角面片a8所示，系统精度达不到此时的尺寸范围，这样的面片可以忽略不计，对整体的分层没有影响，只需要计算与其共边的其他三角面片，最后转化为两个顶点接近分层面的情况。

2.5连接截交线段

对相交的三角面片和分层面完成截交线的计算以后，得到的是一层层无序的线段，并没有实现对STL模型的分层。对于每层的截交线段按照一定的顺序连接起来，组成一层层独立的封闭轮廓，这些封闭轮廓实现了STL模型的分层。图5为直线与三角面片的相交实例。

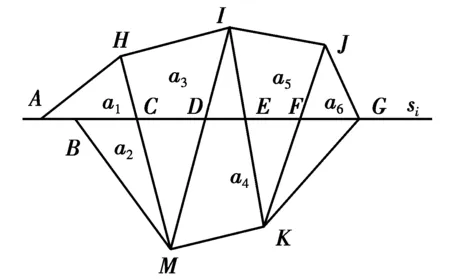
图5　直线与三角面片的相交实例

传统的连接方式都是对端点的重复计算，即是两共边的三角面片，在连接截交线段时，截交线段的两端点被重复计算。如图5所示，当连接a3、a4、a5与分层面si的交线段CD、DE、EF时，端点D、E均被计算两次，在判定三角面片与分层面是否相交时，还要对端点进行计算，增加了计算量，降低了算法的效率，因此，需要对该算法进行改善。

当三角面片a3、a4、a5与分层面si计算得到相交线CD、DE、EF后，并不直接计算交点，而是将其存放在指定的存储容器内，此时V的内容也将发生改变。如图5所示，当a3、a4、a5与分层面si计算完成交线以后，将交线{(J,K),(I,K)}、{(I,M),(H,M)}存入V中。当出现图5所示的a1、a6与分层面si相交时，截交线段分别为{(A,A),(C,C)}和{(G,G),(J,K)}，a2同a1。

当完成所有截交线段的计算以后，将每一层的截交线相连，构成封闭轮廓，完成STL模型的分层，具体实现过程如下：

首先，判定散列表V是否为空，若为非空，则任取一个三角面片ai对应的一组两线段端点{(xi,yi),(xi+1,yi+1)}，并与对应的相交分层面si求交线段，把得到的交线段存入新的容器V_P中。接着在V中取出与ai共(xi+1,yi+1)边的ai+1所对应的一组线段端点{(xi+1,yi+1),(xi+2,yi+2)}，并计算其与分层面si的交线段，将结果存入V_P中，由于V_P中已经存有(xi+1,yi+1)，则将此次的(xi+1,yi+1)舍去，将(xi+2,yi+2)存入V_P中。以(xi+2,yi+2)为搜索对象在V中选取与(xi+2,yi+2)共边的三角面片，直至不再有相同的端点，完成一个封闭环的求交计算。

然后，再判定散列表V是否为空，如果仍为非空，则说明存在多条封闭环，按照上述步骤循环计算，直至V中的元素为空，结束计算，完成所有的截交线的连接，各封闭环的集合实现了对STL模型的分层。

3实例验证

针对上述算法进行实例验证，图6为278 206个三角面片的人头雕塑STL模型，设置分层厚度t为5 mm，对图6模型进行分层实验，按照本文算法经过分层、求交、计算并连接截交线段等程序，多次实验得到侧面局部分层效果图，见图7。由图7可知：分层效果均匀性较好，没有出现计算过程中算法失效或分层轮廓中断的情况。此外，改变分层厚度，可以得到不同厚度的分层效果，算法方便灵活，无论是算法的计算量还是模型的分层质量，都能够较好地满足要求，体现了本文算法的可靠性。为验证本文算法的高效性和稳定性，采用文献[10]的分层算法对图8所示的4个三角面片显示的STL模型进行分层，与本文算法进行对比。其中，模型1、模型2、模型3和模型4的三角面片数量分别为16 776、40 152、128 800和230 206，分层厚度均设置为 5 mm。图9为本文算法与文献[10]算法分层时间对比图。由图9可知：两种算法均能够快速实现对各模型的分层计算，三角面片在10 000个以下时，两种算法的分层时间相差不明显；三角面片数量超出10 000个后，本文算法相对文献[10]的计算效率提高了10%以上，具有较高的计算效率。文献[10]的算法随着三角面片数量的增多，分层时间迅速增加，时间变化率较大，而本文算法在三角面片数量较多时分层时间也有所增加，但时间变化率较小，且较为稳定，表明本文算法的稳定性较好。

图6人头雕塑STL模型

图7侧面局部分层效果

图8 　STL三角网格模型

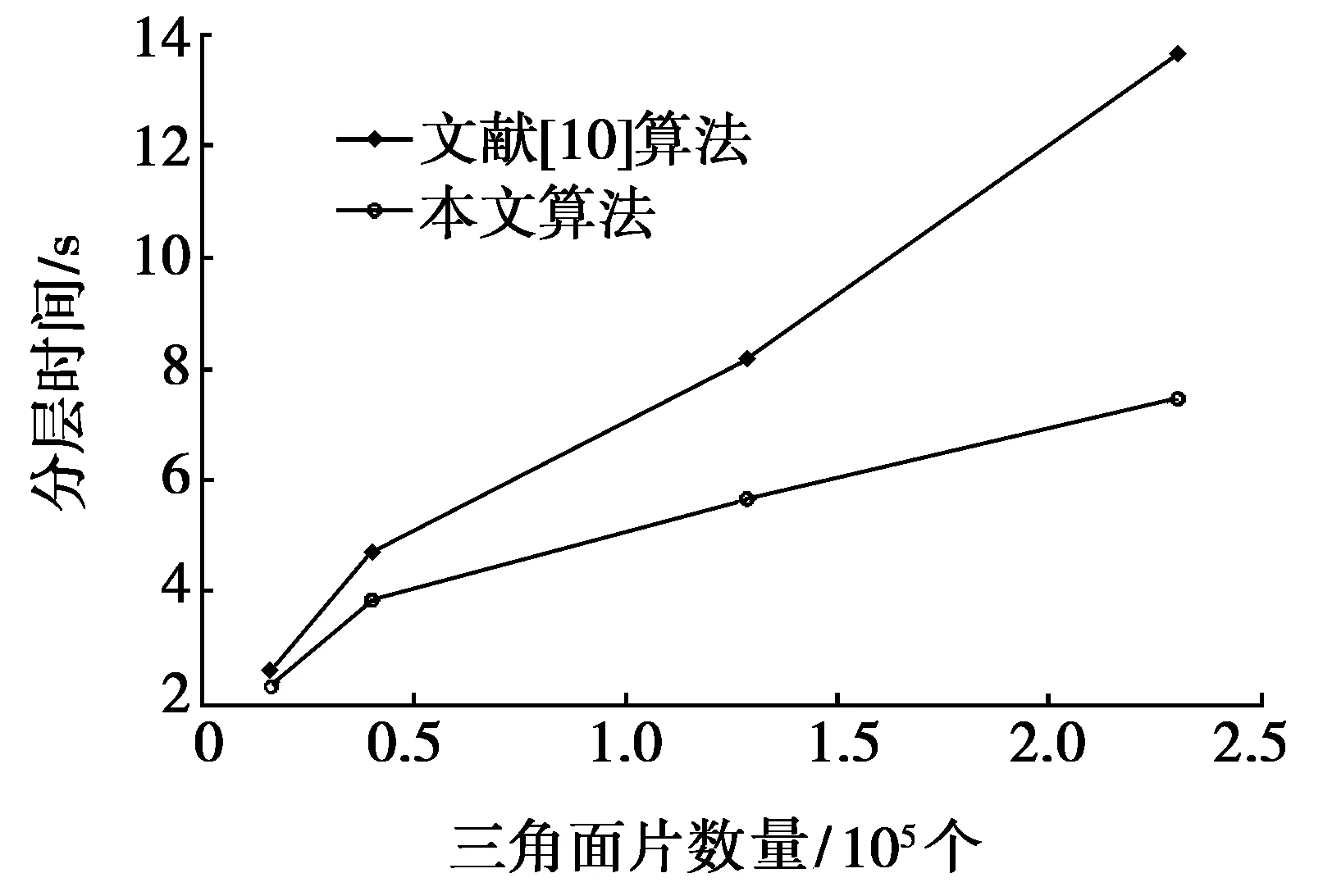
图9　本文算法与文献[10]算法分层时间对比

4结论

(1)建立了空间散列表索引结构，可对各种STL模型进行分层，算法适应性强。

(2)除去了不相交三角面片计算量，提高了计算效率，节省储存空间。

(3)轮廓误差的分析处理，明确了三角面片与分层平面位置关系，降低了计算时无效判断使程序终止计算的效率。

参考文献：

[1]孙殿柱,朱昌志,李延瑞.三角网格曲面模型快速分层算法[J].北京航空航天大学学报(自然科学版),2010,36(3):279-282.

[2]朱晓涛.面向正则体积显示的三维模型体素化研究[D].杭州:浙江大学,2013:28-45.

[3]王素,刘恒,朱心雄.STL模型的分层邻接排序快速切片算法[J].计算机辅助设计与图形学报,2011,23(4):600-606.

[4]蒋恒恒,李奇敏,汤宝平.基于数学形态学与拓扑规则的三角网格修补算法[J].机械工程学报,2013,49(1):148-155.

[5]刘磊.三维网格特征提取与分割[D].上海:华东师范大学,2015:42-50.

[6]董洪伟.三角网格分割综述[J].中国图像图形学报,2010,15(2):181-193.

[7]BOSCHETTO A,BOTTINI L.Triangular mesh offset aiming to enhance fused deposition modeling accuracy[J].International journal of advanced manufacturing technology,2015,80(1):99-111.

[8]HOLGATE N,JOLDES G R,MILLER K.Efficient visibility criterion for discontinuities discretized by triangular surface meshes[J].Engineering analysis with boundary elements,2015,58:1-6.

[9]王春香,郝志博.快速成型技术STL模型等厚分层算法研究[J].机械设计与制造,2014(4):133-136.

[10]王春香,李振华.STL模型分层算法的优化及应用[J].机械设计与制造,2013(3):87-90.

基金项目：河南省重点科技攻关基金项目(152102210281);河南省高等学校重点科研基金项目(16A460017);河南科技大学青年科学基金项目(2015QN005)

作者简介：段明德(1966-),男,河南洛阳人,教授,硕士，硕士生导师,主要研究方向为CAD/CAM/CAE逆向工程.

收稿日期：2016-01-31

文章编号：1672-6871(2016)05-0011-05

DOI:10.15926/j.cnki.issn1672-6871.2016.05.003

中图分类号：TP391.4

文献标志码：A