水下环肋圆柱壳的振动耦合频率影响因素分析

陈金晓，梁　斌，李　戎，徐红玉

(1.河南科技大学 土木工程学院,河南 洛阳 471023；2.九州工业大学 机械系，日本 北九州 804-8550)



水下环肋圆柱壳的振动耦合频率影响因素分析

陈金晓1，梁斌1，李戎2，徐红玉1

(1.河南科技大学 土木工程学院,河南 洛阳 471023；2.九州工业大学 机械系，日本 北九州 804-8550)

摘要：在Flügge理论的基础上，考虑流体的影响，通过波动法推导出静水压力下环肋圆柱壳耦合振动特征方程，并利用牛顿迭代法求得耦合振动频率。将静水压力下圆柱壳与环肋圆柱壳的计算结果进行了对比，验证了本文方法的正确性和有效性。通过算例分析了在不同边界条件下，环肋形式、静水压力、圆柱壳尺寸、环肋尺寸和环肋数目等因素对静水压力下环肋圆柱壳耦合频率的影响。研究结果表明：在静水压力下，肋条的存在增强了圆柱壳的振动强度，耦合作用的存在降低了圆柱壳的振动强度。连续静水压力下，随着静水压力的增大，圆柱壳的振动强度不断减弱；圆柱壳尺寸、肋条尺寸和环肋数目的改变在不同程度上改变了圆柱壳的耦合频率。

关键词：静水压力；环肋；圆柱壳；波动法；耦合频率

0引言

环肋圆柱壳是一类重要的工程结构，在航空器、宇航飞行器、舰艇以及水下潜艇结构中广泛应用。研究静水压力下环肋圆柱壳耦合振动特性的影响因素，对水下环肋圆柱壳的安全设计具有重要意义。文献[1]采用无损预报方法计算了水下环肋圆柱壳弹性失稳的临界荷载，分析了边界条件对水下环肋圆柱壳临界荷载的影响。文献[2]在传递矩阵法的基础上，研究了变厚度环肋圆柱壳的振动特性。文献[3]利用Flügge方程和Helmholtz波动方程，在振动方程中把静水压力当做额外应力考虑，研究了静水压力对环肋圆柱壳输入功率流的影响。文献[4-5]采用波动法研究了圆柱壳的自由振动。文献[6]采用能量法，引入应变能因子，讨论环肋与壳体之间的相互作用，分析了环肋圆柱壳的振动特性。文献[7]在Love壳体理论和波动法基础上，分析了环肋形式、肋条尺寸和肋条数目等因素对充液环肋圆柱壳耦合振动的影响。文献[8]在Flügge理论的基础上，考虑流体与圆柱壳接触面的耦合作用，研究了静水压力等因素对水下环肋圆柱壳耦合振动的影响。但是，综合考虑环肋形式和静水压力等组合因素，关于圆柱壳耦合振动特性方面的研究还存在着大量空白。

本文基于Flügge理论利用波动法并考虑流体影响，得到静水压力下环肋圆柱壳耦合系统的运动方程。采用牛顿迭代法求解出静水压力下不同环肋形式圆柱壳的耦合频率，研究了环肋形式和边界条件等因素对圆柱壳耦合频率的影响。

1理论分析

本文采用的静水压力下环肋圆柱壳及环肋截面模型，如图1所示。图1中：R为平均半径；L为圆柱壳长度；h为圆柱壳壁厚；O为圆柱壳圆形截面的圆心；hr为肋条截面高度；br为肋条截面宽度；d2为肋条间距；e2为环肋的偏心距(不同的环肋形式，环肋偏心距的取值不同，见文献[9])。在圆柱壳的中面上建立正交坐标系(x,θ,z)，其中，x、θ和z分别为圆柱壳的轴向、环向和径向坐标。

用波动法表示的圆柱壳振动位移方程为：

(1)

其中：Um,Vm,Wm分别为x,θ,z方向的波幅；n为周向波数；i2=-1；ω为固有角频率；t为时间；km为轴向波数，其大小与边界条件有关；x,θ分别为圆柱壳的轴向和环向坐标。

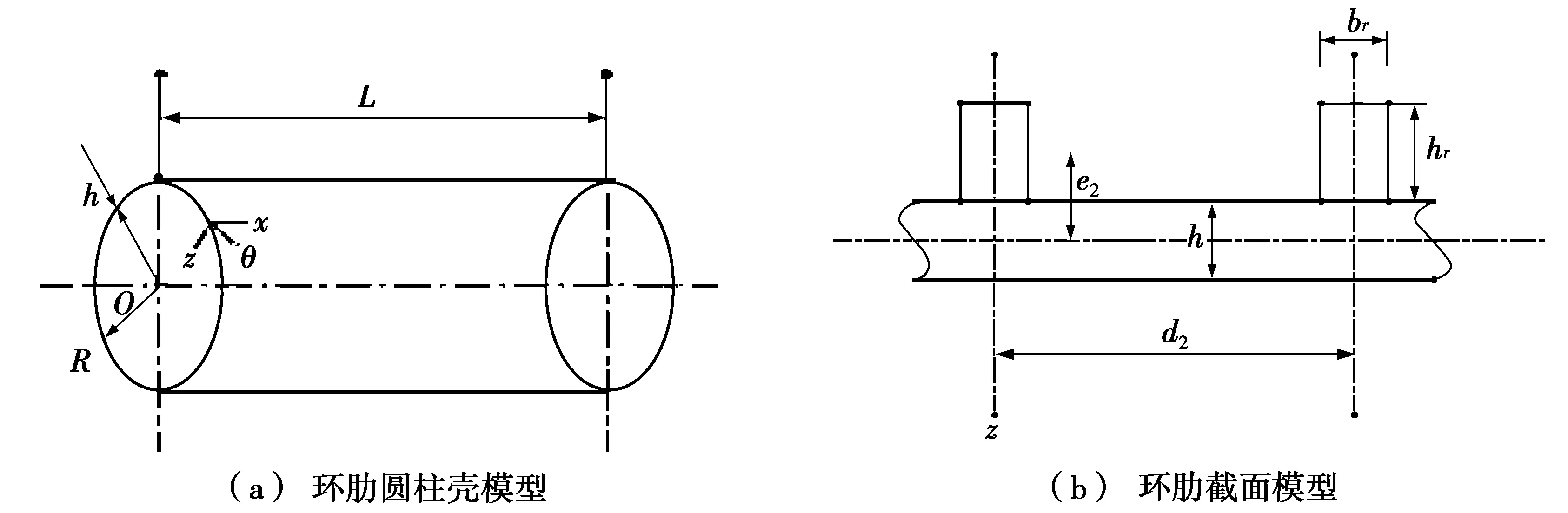
图1　静水压力下环肋圆柱壳及环肋截面模型

将方程(1)代入静水压力下环肋圆柱壳的运动方程[10]，得到用矩阵表示的静水压力下振动系统的运动方程为：

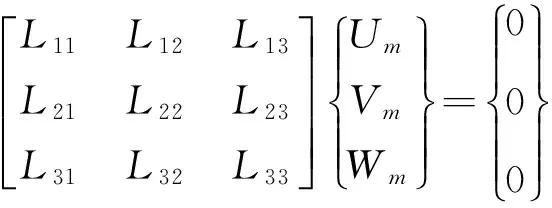
(2)

计算中,需要考虑流体与圆柱壳结构的耦合效应，在流体中用柱坐标表示的声压方程为：

ψ=ψmcos(nθ)Jn(krr)eiωt-ikm，

(3)

在圆柱壳外壁与流体的接触界面上，需要满足流体径向位移与圆柱壳径向位移必须相等的耦合条件，其表达式为：

(4)

(5)

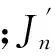
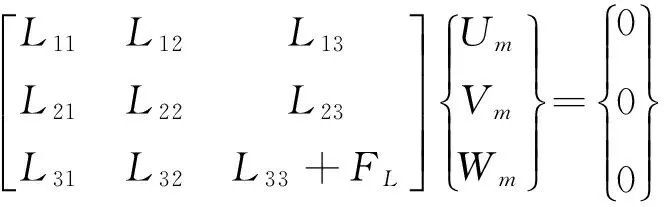
(6)

其中：FL为流体声场作用所产生的流体荷载项,

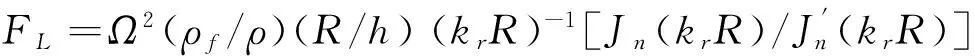
(7)

当FL=0,静水压力Q=0 kPa时，方程(7)可以还原为不考虑流体影响的环肋圆柱壳固有频率的求解，方程(2)可以求解不考虑流体影响的静水压力下环肋圆柱壳的固有频率，方程(7)是一个超越方程，可以运用牛顿迭代法求解环肋圆柱壳的耦合频率。

2算例与讨论

本文通过退化计算来验证理论研究的有效性和正确性，计算结果见表1与表2。表1退化计算了两端简支边界条件下环肋圆柱壳在不同模态(m,n)下的固有频率(m为轴向半波数，n为周向波数)，将计算结果与文献[11]中的计算结果进行了对比。表2退化计算了两端简支(SS-SS)、两端固支(C-C)和一端固支一端自由(C-F)这3种边界条件时，静水压力下不加环肋圆柱壳的耦合频率，将计算结果与文献[12]中的计算结果进行了对比。两类退化计算的结果对比，验证了本文计算的有效性和正确性。

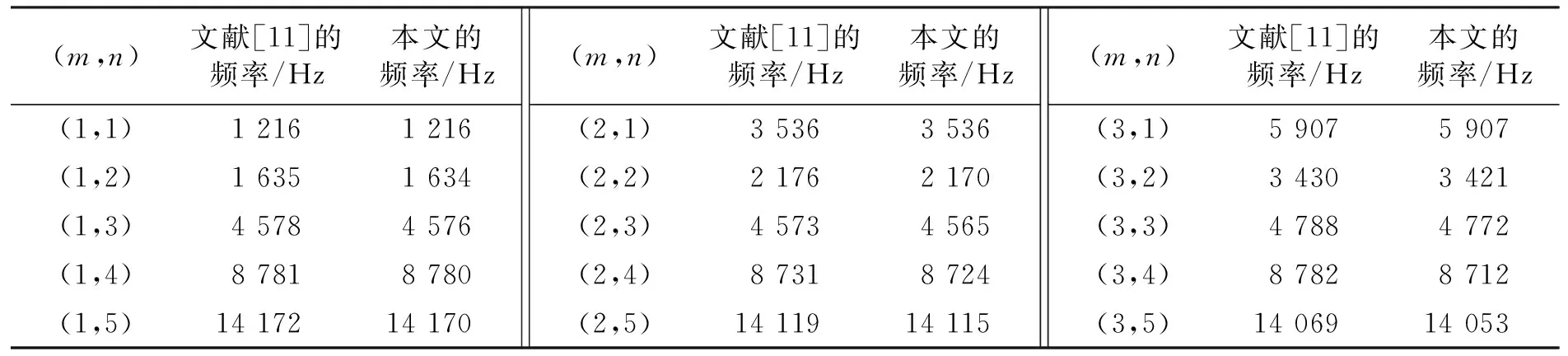
表1 　两端简支边界条件下环肋圆柱壳固有频率计算结果对比分析

表2　不同边界条件时静水压力下不加环肋圆柱壳耦合频率计算结果对比分析

在计算静水压力下环肋圆柱壳耦合频率时，需要考虑结构稳定性。当固有频率为0 Hz时，所对应的静水压力可认为是临界静水压力。本文算例中，静水压力皆控制在临界静水压力以上，即耦合频率均控制在0 Hz以上。算例中分析了连续静水压力下环肋圆柱壳耦合频率的变化规律,以及不同轴向半波数、环肋形式、圆柱壳尺寸、肋条尺寸和环肋数目等影响因素下耦合频率的变化规律。计算结果见图2至图6，本文选用的圆柱壳几何参数为：E=2.06×1011N/m2，υ=0.3，ρ=7 800 kg/m3，L=20 m，R=1 m，h=0.002 m，hr=0.005 82，br=0.002 18，m=1，n=2，肋条数目N=19。

图2是以两端简支边界条件下的环肋圆柱壳作为研究对象，分析了在连续静水压力Q下不同环肋形式圆柱壳耦合频率变化规律。从图2中可以看出：3种环肋形式圆柱壳耦合频率均随着静水压力的增大而不断减小，耦合频率在接近临界静水压力时下降幅度增大；3种环肋形式圆柱壳，内环肋圆柱壳耦合频率最大，对称环肋圆柱壳耦合频率最小。

图2两端简支边界条件时不同静水压力下环肋圆柱壳的耦合频率变化曲线

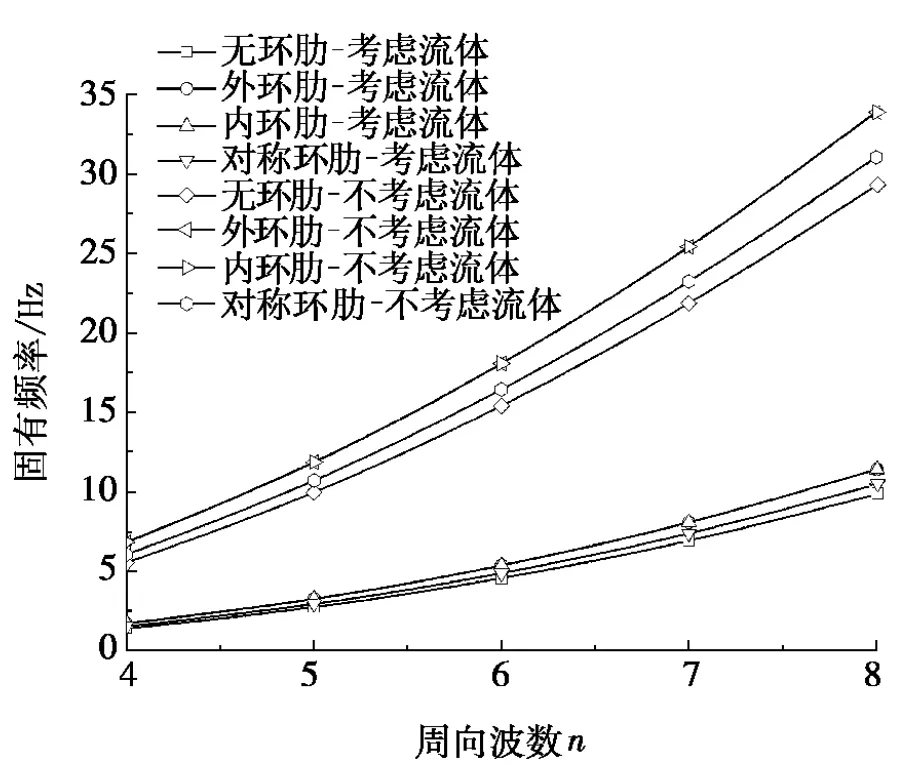
图3两端简支边界条件下不同环肋形式圆柱壳的固有频率变化曲线

图3以不同环肋形式为出发点，分析了静水压力Q=1 kPa时，考虑流体影响和不考虑流体影响两种条件下圆柱壳固有频率的变化规律。从图3中可以看出：固有频率随着周向波数n的增大而增大；环肋圆柱壳固有频率高于不加肋圆柱壳固有频率。3种环肋形式的圆柱壳固有频率，外环肋圆柱壳与内环肋圆柱壳非常接近，内环肋圆柱壳略大于外环肋圆柱壳，而外环肋圆柱壳大于对称环肋圆柱壳。流体对圆柱壳固有频率的影响比较显著，不考虑流体影响的圆柱壳固有频率明显高于考虑流体影响的圆柱壳耦合频率。

基于上述结论，下面以内环肋形式和静水压力Q=5 kPa为研究对象进行讨论。图4分析了两端简支(SS-SS)和两端固支(C-C)两种边界条件时，不同轴向半波数m条件下圆柱壳耦合频率随h的变化规律。从图4中可以看出：两端固支圆柱壳耦合频率大于两端简支圆柱壳耦合频率。耦合频率随着h增大而不断增大。随着轴向半波数m的增大，耦合频率也不断增大，且耦合频率的增长幅度变大。

图5分析了两端简支(SS-SS)和两端固支(C-C)两种边界条件下不同圆柱壳长度L时，圆柱壳耦合频率的变化规律。由图5可看出：圆柱壳耦合频率随着圆柱壳长度L的增大而减小，但随着L的增长，耦合频率的下降幅度减小。当L=5 m时，随着圆柱壳厚度h的增大，耦合频率的增大幅度比较明显。当L增大到20 m，随着h的增大，耦合频率的增大速度趋于平缓。两端固支圆柱壳耦合频率明显高于两端简支圆柱壳耦合频率。

图4不同m下圆柱壳的耦合频率变化曲线

图5不同L下圆柱壳的耦合频率变化曲线

图6　不同hr/br时圆柱壳的耦合频率变化曲线

图6 以不同肋条数目N为出发点，分析了两端简支(SS-SS)和两端固支(C-C)两种边界条件下肋条截面高度与宽度之比hr/br不同时，圆柱壳耦合频率的变化规律。从图6中可以看出:圆柱壳耦合频率随着N的增加而增大。两端简支时，随着hr/br的增大，耦合频率的增大速度变快，而两端固支时这种现象并不明显。耦合频率随着hr/br的增大而增大，两端简支时增大幅度更加明显。两端固支时的耦合频率明显大于两端简支时的耦合频率。

3结论

(1)环肋对水下圆柱壳耦合频率的影响比较显著，在连续静水压力下，3种环肋形式圆柱壳耦合频率均明显高于不加肋圆柱壳耦合频率。3种环肋圆柱壳耦合频率相比较，内环肋圆柱壳耦合频率最大，对称环肋圆柱壳耦合频率最小。

(2)环肋圆柱壳和不加环肋圆柱壳的耦合频率均随着静水压力增大而减小，流体对圆柱壳结构的耦合效应比较明显，耦合效应的存在大大降低了圆柱壳固有频率。

(3)静水压力下环肋圆柱壳耦合频率随着圆柱壳厚度h增大而增大，增大速度随着轴向半波数m增大而加快；耦合频率随着圆柱壳长度L增大而不断减小，当L较小时，频率减小速度较快，当L不断增大时，频率减小速度明显减慢。

(4)圆柱壳耦合频率随着肋条截面高度hr与肋条截面宽度br比值的增大而增大，但增大幅度相对比较缓慢。与h、L对耦合频率的影响相比，hr/br对耦合频率的影响相对比较弱。在静水压力下，随着肋条数目N的增大耦合频率不断增大，但是增大的速度比较缓慢。

(5)连续静水压力下，两端固支环肋圆柱壳耦合频率均高于两端简支环肋圆柱壳耦合频率。

参考文献：

[1]陈忱,李天匀,朱翔,等.水下环肋圆柱壳弹性失稳临界荷载无损预报方法[J].海洋工程,2014,32(4):89-95.

[2]曹雷,马运义,黄玉盈.环肋加强变厚度圆柱壳的自由振动[J].华中科技大学学报(城市科学版),2007,24(2):63-66.

[3]LIU Z Z,LI T Y,ZHU X,et al.Effect of hydrostatic pressure on input flow in submerged ring-stiffened cylindrical shells[J].Journal of ship mechanics,2011,15(3):301-312.

[4]LI X B.Study on free vibration analysis of circular cylindrical shells using wave propagation[J].Journal of sound and vibration,2008,311(3/5):667-682.

[5]ZHANG X M,LIU G R,LAM K Y.Vibration analysis of thin cylindrical shells using wave propagation approach[J].Journal of sound and vibration,2001,239(3):397-403.

[6]李学斌.环肋圆柱壳自由振动分析的能量法[J].船舶力学,2001,5(2):73-81.

[7]LIU X W,LIANG B,LI R.Effect of stiffening parameters on vibration characteristics of fluid-filled cylindrical shells with ring-stiffener[J].Journal of ship mechanics,2015,19(3):294-302.

[8]LIANG B,LIU X W,LI R.Study on coupled vibration of ring-stiffened cylindrical shells subjected to hydrostatic pressure using wave propagation method[J].Journal of ship mechanics,2013,17(1/2):148-154.

[9]ZHOU X P.Vibration and stability of ring-stiffened thin-walled cylindrical shells conveying fluid[J].Acta mechanica solida sinica,2012,25(2):168-176.

[10]中国科学院研究所固体力学研究室板壳组.加筋圆柱曲板与圆柱壳[M].北京:科学出版社,1983:353-358.

[11]GAN L,LI X B,ZHANG Z.Free vibration analysis of ring-stiffened cylindrical shells using wave propagation approach[J].Journal of sound and vibration,2009,326(3/5):633-646.

[12]ZHU X,YE W B,LI T Y,et al.The elastic critical pressure prediction of submerged cylindrical shell using wave propagation method[J].Ocean engineering,2013,58(1):22-26.

基金项目：国家自然科学基金项目(51105132,11402077);河南省自然科学基金项目(122300410112)

作者简介：陈金晓(1991-),女,河南南阳人,硕士生;梁斌(1963-),男,河南洛阳人,教授,博士，博士生导师,主要研究方向为工程结构非线性分析与优化设计.

收稿日期：2015-12-03

文章编号：1672-6871(2016)05-0041-05

DOI:10.15926/j.cnki.issn1672-6871.2016.05.010

中图分类号：TB535+.1

文献标志码：A