基于傅里叶梅林变换的SURF算法
2016-07-23廖萌萌
那 彦, 廖萌萌
(西安电子科技大学 电子工程学院,陕西 西安 710071)
基于傅里叶梅林变换的SURF算法
那彦, 廖萌萌
(西安电子科技大学 电子工程学院,陕西 西安 710071)
摘要针对加速鲁棒性特征算法,在没有后续去误匹配等处理的情况下,对存在较大旋转角度的两幅待匹配图像,匹配精度较低的问题,提出了一种基于傅里叶梅林变换的SURF算法。该算法通过对待匹配图像和参考图像实施傅里叶变换和梅林变换,利用能量谱求出两幅图像发生的旋转角度,并利用SURF算法找出图像间发生的平移和尺度变化,实现了图像间的匹配。实验结果表明,该算法可有效地实现图像间存在较大旋转角度时的几何匹配,且相比已有的SIFT和SURF算法,具有更好的匹配效果。
关键词图像处理;图像匹配;傅里叶梅林变换
图像匹配是通过几何变换将待匹配图像和参考图像中相同内容或相同结构对准的过程。图像匹配广泛用于计算机视觉[1]、模式识别[2]、医学图像处理[3]、遥感图像处理[4]等领域。实现图像间匹配当前用的较多的是基于求解物理模型的匹配方法,该方法大致分为3类:基于灰度的图像匹配算法、基于特征的匹配算法以及基于变换域的匹配算法。总体而言,各种方法各有优缺点。SURF(SpeedUpRobustFeatures)算法是基于特征的匹配算法中比较常用的算法,在没有使用后续去除误匹配算法的情况下,其不能很好地处理图像间存在较大旋转角度的匹配,且有些去除误匹配算法去除误匹配的效果不是很好,且增加去误匹配算法会增加总的匹配时间,针对这一问题,本文提出了基于傅里叶梅林变换的SURF算法。
1SURF算法
SURF算法利用两幅图像间共同的特征从而实现图像的匹配,通常包括特征提取、特征关联、参数优化求解以及图像重采样等环节。
1.1SURF角点提取算法提取特征
SURF算法利用海森矩阵的行列式来确定特征点的位置,Lxx(x,y,σ)、Lxy(x,y,σ)、Lyy(x,y,σ)分别是输入图像卷积高斯函数的二阶导数形成的[5]。海森矩阵的表达式如下
(1)
为简化计算海森矩阵的行列式,用式(2)计算[6]
Det(H)=DxxDyy-(0.9Dxy)2
(2)
利用式(2)求出每个点的海森矩阵行列式后,在某点3×3×3的立体区域进行非极大值抑制。通过比较本尺度某点周围8个点以及上下尺度9个点共26个邻域值,取最大或最小的作为特征点[7]。
1.2特征关联
计算在以每一个特征点为中心,半径为6 ( 为该特征点对应的尺度)的圆形区域内点的哈尔小波响应,并给这些响应值分配高斯权值,以特征点为中心,滑动角度范围为π/3的扇形窗口,将角度范围为π/3的扇形区域里经过加权的响应值全部相加得到一个合成矢量。选取模值最大的矢量方向为该特征点的主方向。
以每一个特征点为中心,以其主方向为一个坐标轴,选取边长为20σ(σ为特征点的尺度)的正方形区域,将该区域分成4×4的子区域,计算每个子区域内的水平方向哈尔小波响应dx和垂直方向哈尔小波响应dy,并给每个响应值赋高斯权值,然后将每个子区域的响应值相加得到∑dx和∑dy。将每个子区域的响应值的绝对值相加得到∑|dx|和∑|dy|。每个子区域可以用一个四维向量表示v=(∑dx,∑|dx|,∑dy,∑|dy|),因此,对于每一个特征点,形成 维特征向量,对向量进行归一化处理。
计算待匹配图像中特征点的特征向量与参考图像中特征点的特征向量的距离,利用最近距离比次近距离的方法进行特征关联[7]。
1.3参数优化求解
利用关联好的特征点对的坐标,使用最小二乘法求出变换模型的参数。
1.4图像重采样
利用双线性插值算法进行插值,最终得到匹配图像。
2基于傅里叶梅林变换的SURF算法
2.1算法原理
基于傅里叶梅林变换的SURF算法,先利用傅里叶梅林变换[8]的相关知识求得待匹配图像和参考图像间的旋转角度,然后利用求出的旋转角度矫正待匹配图像,得到初步匹配图像,进而利用SURF算法匹配得到的初步匹配图像和参考图像,从而得到最终的匹配图像。
2.2傅里叶梅林变换
假定待匹配图像为f2(x,y),参考图像为f1(x,y),f1(x,y)与f2(x,y)之间的关系如式(3)所示。
f2(x,y)=f1[a(xcosθ0+ysinθ0)-Δx,
a(-xcosθ0+ysinθ0)-Δy]
(3)
式(3)中,a为尺度变换因子,θ0为待匹配图像和参考图像间的旋转角度,Δx和Δy为f(x,y)与f2(x,y)间的水平平移量和垂直平移量。
|f2(ξ,η)|=a-2|F1[a-1(ξcosθ0+ηsinθ0+ηsinθ0),
a-1(-ξsinθ0+ηcosθ0)]|
(4)
(5)
令λ=lgρ,b=lga,并定义rp1(θ,λ)=rp(θ,ρ),sp1(θ,λ)=sp(θ,ρ),则有
sp1(θ,λ)=a-2rp1[(θ-θ0),λ-b]
(6)
对式(6)运用傅里叶变换,并利用交叉能量谱公式即可求出θ0。
2.3SURF算法再匹配
求出待匹配图像和参考图像间的旋转角度之后,利用求出的角度矫正待匹配图像,得到初步匹配图像,然后使用SURF算法对得到的初步匹配图像和参考图像进行匹配,从而得到最终的匹配图像。
3实验结果及分析
为验证本文提出的算法的有效性,分别使用SIFT(ScaleInvariantFeatureTransform)算法、SURF算法以及本文提出的基于傅里叶梅林变换的SURF算法对待匹配图像和参考图像在不同旋转角度差下进行了实验。本文使用相关系数来衡量匹配方法的匹配精度。
假设图像A和图像B的尺寸为m×n,则图像A和图像B的相关系数CAB定义如下
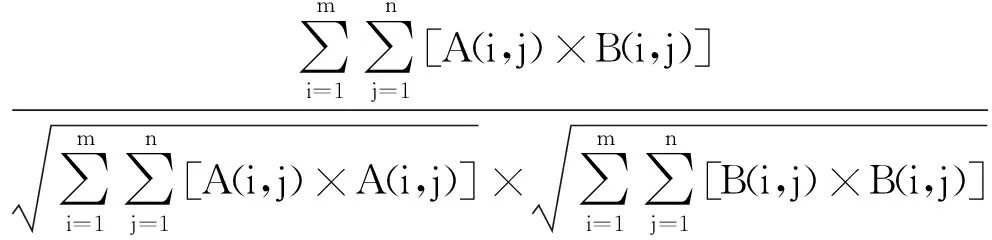
图1为用于实验的待匹配图像和参考图像。
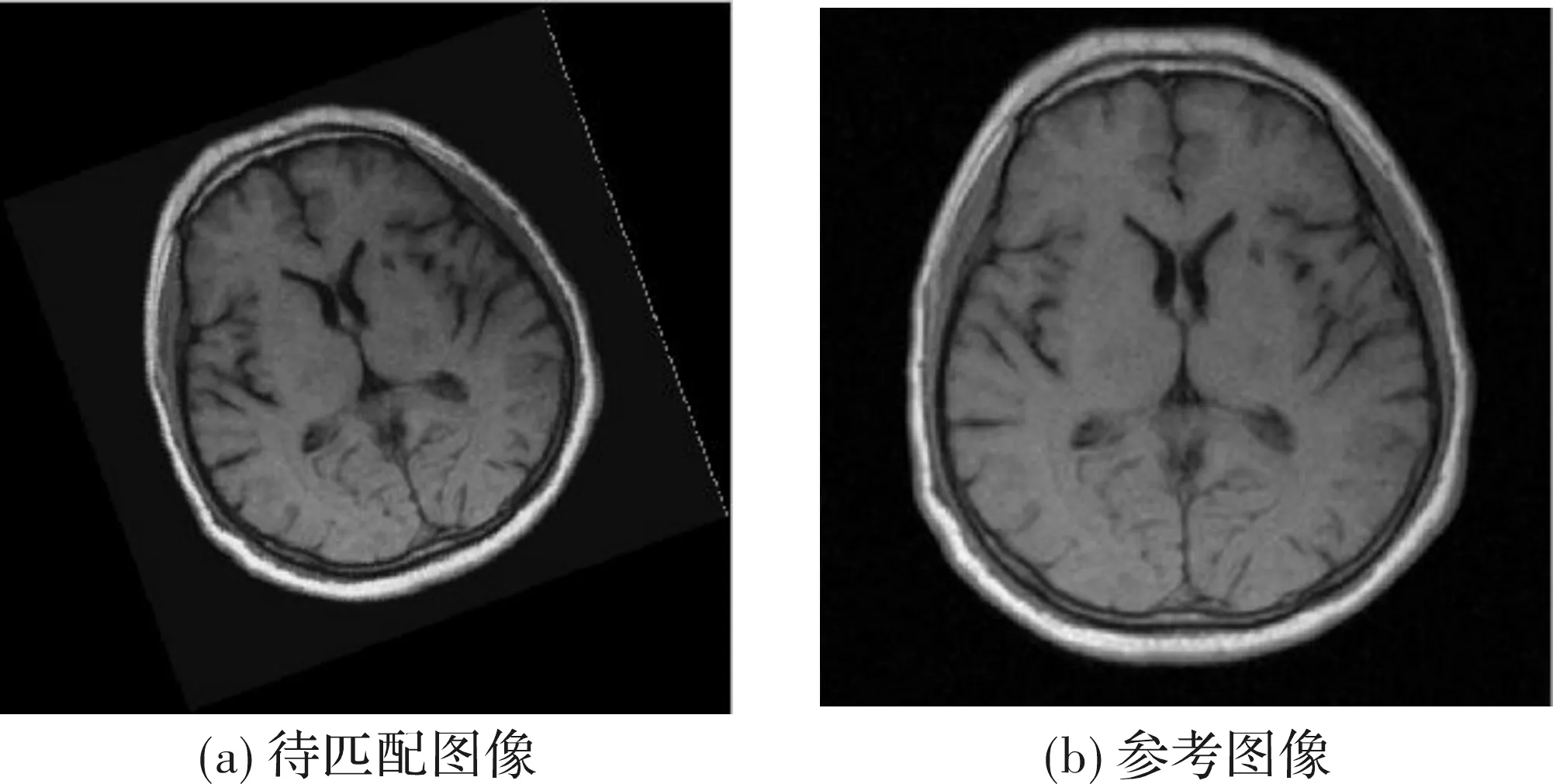
图1 待匹配图像和参考图像
将SIFT算法、SURF算法以及本文提出的基于傅里叶梅林变换的SURF算法的匹配结果列于表1和表2中,表1为3种匹配方法处理待匹配图像和参考图像在不同旋转角度差下的匹配精度表,表2为3种匹配方法的匹配时间表。

表1 3种匹配方法匹配精度表

表2 3种匹配方法匹配时间表 /s
图2是待匹配图像和参考图像间旋转角度为50°时,3种匹配算法的匹配结果图。

图2 3种匹配算法匹配结果图
从表1中可看出,本文提出的算法可以有效解决图像间存在较大旋转角度的匹配,且匹配精度基本在0.96以上。SIFT算法和SURF算法在处理图像间旋转角度>20°的匹配时,匹配精度都<0.9,且随着角度的增大,匹配精度呈下降趋势。
从表2中可看出,本文提出的算法匹配时间基本和SURF算法相当,且远低于SIFT算法的匹配时间。
4结束语
当前基于特征的图像匹配算法中较为常用的SIFT算法和SURF算法,在处理旋转角度较大的两幅图像间的匹配时,匹配效果不是很好,通常需要后续的去误匹配算法来矫正匹配效果,但有些去误匹配算法矫正效果并不理想,且增加了去误匹配算法会延长整个算法的匹配时间。
因此,本文提出了一种无须增加误匹配算法也可处理图像间存在较大旋转匹配的算法——基于傅里叶梅林变换的SURF算法。该算法利用傅里叶梅林变换先求出两幅图像间发生的旋转角度,从而首先矫正两幅图像间发生的旋转,然后利用SURF算法匹配初步得到的匹配图像和参考图像,最终完成两幅图像间的匹配。实验结果证明,本文提出的基于傅里叶梅林变换的SURF算法,不仅可处理图像间旋转角度较小的匹配,还能有效处理图像间旋转角度较大的匹配,且比起已有的SIFT和SURF算法,具有更好的匹配效果。
参考文献
[1]王红梅,张科,李言俊.图像匹配研究进展[J].计算机工程应用,2004, 40(19):42-44.
[2]魏宁.模式识别中图像匹配快速算法研究[D].兰州:兰州大学,2009.
[3]朱广新.基于特征点匹配的图像拼接及医学应用[D].南京:南京理工大学,2007.
[4]郑悦,程红,孙文邦,等.遥感影像匹配技术研究[J].电子设计工程,2011,19(20):97-100.
[5]时磊,谢晓方,乔勇军.基于SURF算法的人脸跟踪技术研究[J].计算机仿真,2010,27(12):227-231.
[6]MaLW,SongZ,ZhuGH.AnimprovedSURFalgorithmbasedlocalimagesymmetryscoringscheme[C].Dalian:the7thInternationalCongressonImageandSignalProcessing,2014.
[7]BayH,EssA,TuytelaarsT.SURF:speededuprobustfeatures[C].Graz:The9thEuropeanConferenceonComputerVision, 2006.
[8]安晓东.基于Fourier-Mellin变换的宽视场监控图像合成技术[J].中北大学学报:自然科学版,2007,28(2):181-183.
A SURF Algorithm Based on the Fourier Merlin Transform
NAYan,LIAOMengmeng
(SchoolofElectronicEngineering,XidianUniversity,Xi’an710071,China)
AbstractA SURF algorithm based on the Fourier Merlin transform is proposed to improve the registration accuracy of speed up robust features in dealing with the registration when there is large rotation between images under the condition that no removal error registration algorithm. The floated image and reference image are Fourier transformed and Merlin transformed by the proposed algorithm, after which the rotation angle between two images is computed by using the energy spectrum, and the changes of translation and scale between the two images are computed by the SURF algorithm, thus realizing the registration of two images. Experimental results show that the registration with large rotation between two images can be effectively realized by the proposed algorithm with better registration result than that by the SIFT algorithm and the SURF algorithm available.
Keywordsimage processing; image registration; fourier merlin transform
收稿日期:2015- 11- 16
作者简介:那彦(1964-)男,博士,教授。研究方向,图像融合,信号处理。廖萌萌 (1988-)男,硕士研究生。研究方向:图像匹配。
doi:10.16180/j.cnki.issn1007-7820.2016.07.016
中图分类号TP391.41
文献标识码A
文章编号1007-7820(2016)07-055-03
