非线性系统的自适应模糊控制器设计
2016-07-23吴海晴沈昱明
吴海晴,苏 湛,沈昱明
(上海理工大学 光电信息与计算机工程学院,上海 200093)
非线性系统的自适应模糊控制器设计
吴海晴,苏湛,沈昱明
(上海理工大学 光电信息与计算机工程学院,上海 200093)
摘要针对非线性系统,为获得更好的控制控制效果,设计了模糊自适应控制器。在模糊控制器的基础上根据反馈控制和调整参数向量的自适应律的求解,综合李雅普诺夫稳定理论设计了模糊自适应控制器,以满足系统的稳定性和控制效果。为验证控制器的有效性,将该控制器应用到二级倒立摆系统的稳定控制,仿真结果表明该控制器的控制效果良好,并与传统的控制方法相比较,其控制效果更佳。
关键词自适应;模糊控制;李雅普诺夫稳定理论;倒立摆
对于时变、非线性的复杂系统采用模糊控制时,为获得更好的控制效果,必须要求模糊控制具有较完善的基于经验所得的控制规则。由于被控过程中的高阶次、非线性和未知干扰等因素,造成了模糊控制规则不完善,会不同程度的影响控制效果[1-5]。针对这些不确定性因素,自适应控制的目的在于系统出现这些不确定性因素时,可以使系统保持理想的控制特性[6-9]。为得到更理想的控制效果,采用模糊控制和自适应控制相结合的控制方法。本文在模糊控制器设计的基础上,从李雅普诺夫方法的角度上对控制器加入自适应的设计及其稳定性的分析。得到的模糊自适应控制器结合了模糊逻辑控制和自适应控制的优点,使系统的控制效果和稳定性更佳。
1模糊控制器的设计
n阶非线性系统
(1)
式(1)中,u是系统的输入;y是系统的输出,且有u,y∈R,f(·)和g(·)均是未知的连续函数。(x1,x2,…,xn)T属于Rn,是系统的n维状态向量,且假设是可测量的。
1.1输入输出变量及模糊语言描述
根据式(1)中的非线性系统,控制器的输入变量是误差e和误差变化率ec,输出变量为控制变量u。其中e代表跟踪误差,是yd与y的差值。ec是e的一阶导数,代表误差的变化率,u是系统输出的变化量。由于在实际的系统控制过程中,误差e、误差变化率ec和控制变量u是不断变化的,因此需要在模糊量和精确量之间建立一种转换关系。为提高系统的稳态精度,把e分为8个等级,其模糊集为{NB,NM,NS,N0,P0,PS,PM,PB},ec和u的模糊集为{NB,NM,NS,0,PS,PM,PB},其中这8个模糊语言变量分别为,PB(正大),PM(正中),PS(正小),P0(正零),N0(负零),NS(负小),NM(负中),NB(负大)。
1.2控制器的模糊规则设计
模糊控制的目的是,消除输出对于设定值的偏差。在选择控制量时,其原则是当误差e比较小时,要以系统的稳定性为主,选择控制量是要防止系统超调;当误差e比较大时,选择控制量时主要以尽快消除误差为主。所以根据上述消除偏差的规则,控制规则可以得到,如表1所示。
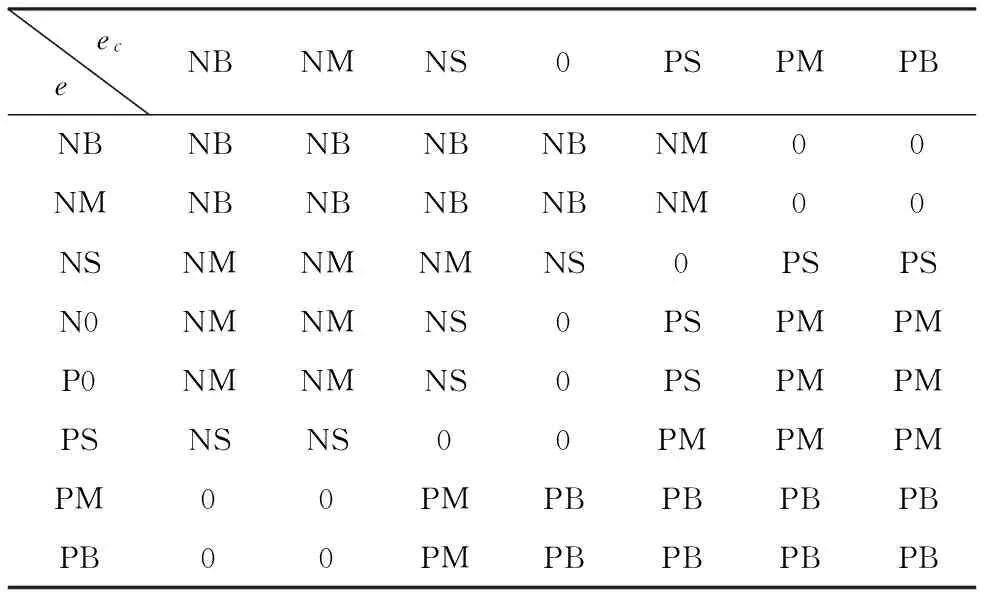
表1 模糊控制器的控制规则
该控制器的模糊规则也可以使用模糊条件语句来描述,如下所示:
(1)ife=NB or NM andec=NB or NM thenu=NB;
(2)ife=NB or NM andec=NS or 0 thenu=NB;
(3)ife=NB or NM andec=PS thenu=NM;
.
.
.
(21)ife=PN or PB andec=PM or PB thenu=PB。
1.3模糊变量的赋值
根据上述模糊控制器的模糊条件语句,以及精确量与模糊量之间的转换关系,假设误差e的变化区间为[-6,6],那么误差e的论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。误差变化ec和误差e的论域相同,控制变量u的变化区间为[-7,7]。确定了模糊变量误差e、误差变化率ec和控制变量u的论域,相当于确定模糊语言变量相对应的隶属度。3个模糊变量,针对其中一个误差e举例,的赋e值表如表2所示。

表2 语言变量e的赋值表
1.4模糊控制表的确定
根据模糊条件语句可以确定相应的模糊关系,如果第一条语句的模糊关系为
r=[(NBe+NMe)×NBu]·[(NBec+NMec)×NBu]
(2)
由模糊变量的隶属度,得到控制量为
u1=min{max[μNBe(i)]
max[μNBec(j);μNMec(j)];μNBu(x)}
(3)
其中,μNBe(i)、μNMe(i)和μNBec(i)、μNMec(i)分别是μNBe、μNMe和μNBec、μNMec对应的i、j元素的隶属度。由此可得其余语句的模糊关系,那么模糊控制量集合为
u=u1+u2+u3+…+u21
(4)
通过最大隶属度法将模糊量进行非模糊化,即选取的控制量为模糊子集中隶属度最大的元素。这样就可以得到由模糊量转化为精确量的控制量,从而得到模糊控制表。
通过上述4个步骤便可以设计出简单的模糊控制器。
2自适应模糊控制器的设计
模糊自适应控制器,是在模糊控制器的基础上加入自适应控制,其主要的目的是,得到一个自适应律和一个反馈控制,使得系统具有全局稳定性。定义自适应模糊控制器的模糊逻辑系统为
(5)
(6)
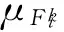
(7)
其中,ki=1,2,3,…,Mi,θf∈R和θg∈R是自适应律,且为常数用来调节参数。
基于式(5)和式(6)模糊逻辑系统的控制律u,其无法满足李雅普诺夫的稳定理论要求,所以加入一个边界控制ud,且为
(8)

使得系统状态在一个限定的范围内并满足李雅普诺夫的理论稳定性。那么控制律为
u=uc+ud
(9)
其中,uc是等效控制,即为模糊逻辑系统的输出。将式(5)代入式(1)得到的误差方程为
(10)
其中,

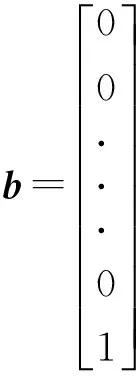
(11)
在E的等式中,T=(tn,tn-1,…,t1)T∈Rn是多项式
h(s)=Sn+t1Sn-1+…+tn
(12)
其解的系数项。
本文采用的自适应律为
(13)
(14)
为简单起见,定义一个ξ(x)为
(15)
根据李雅普诺夫稳定性理论验证该控制器相对这个系统的稳定性。
证明考虑如下的李雅普诺夫函数
(16)

(17)
证明完毕。
由证明过程可得,设计出来的自适应律满足李雅普诺夫稳定理论。所以通过以上步骤设计出来的模糊自适应控制器可以使得系统在闭环状态下处于全局稳定。
3实验结果
根据上述自适应模糊控制器的设计步骤,应用到经典模型二级倒立摆系统上[10]。在简单模糊控制器的基础上加入自适应算法。通过Matlab软件进行仿真实验,结果如图1所示。通过传统简单的模糊控制器进行对二级倒立摆系统稳定控制,Matlab软件仿真结果如图2所示。

图1 自适应模糊控制器的仿真结果
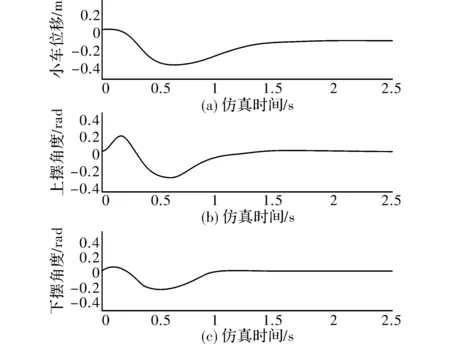
图2 简单模糊控制器的仿真结果
根据图1和图2的仿真结果可以看出,自适应模糊控制和简单模糊控制都可以使二级倒立摆处于稳定状态。由仿真结果也可以看出,自适应模糊控制的结果,在平衡位置的振幅相对简单模糊控制较小,向稳定状态的过渡时间相对较短,所以结果表明自适应模糊控制的可行性,并且能够有效改善控制器的控制精度和动态性能。
4结束语
针对非线性系统,在简单模糊控制器的基础上加
入自适应控制,构造出自适应模糊控制器。为验证控制器的有效性,将该控制器应用到二级倒立摆系统上,通过Matlab仿真,结果表明该控制器的有效性。并与简单模糊控制器在二级倒立摆系统的应用做比对,结果表明,自适应模糊控制器在平衡位置的振幅较小,稳态过度时间较短,有效的改善了控制器的控制精度和动态性能。由此可见本文提出的自适应模糊控制满足系统的稳定性控制,并获得了良好的控制效果。
参考文献
[1]曾光奇,胡军安.模糊控制理论与工程应用[M].武汉:华中科技大学出版社,2006.
[2]李士勇.模糊控制、神经控制和智能控制论[M].哈尔滨:哈尔滨工业大学出版社,1996.
[3]李士勇.模糊控制[M].哈尔滨:哈尔滨工业大学出版社,1996.
[4]韩力群.智能控制理论及应用[M].北京:机械工业出版社,2007.
[5]王立新.模糊系统与模糊控制教程[M].北京:清华大学出版社,2003.
[6]王立新.自适应模糊系统与控制设计与稳定性分析[M].北京:国防工业出版社,1995.
[7]董宁.自适应控制[M].北京:北京理工大学出版社,2009.
[8]方勇纯,卢桂章.非线性系统理论[M].北京:清华大学出版社,2009.
[9]SpoonerJT,PassinoKM.Stableadaptivecontrolusingfuzzysystemsandneuralnetworks[J].IEEETransactionsonFuzzySystems,1996,4(3):339-359.
[10] 焦灵侠,张荷芳.二级倒立摆的模糊控制研究[J].电子设计工程,2009,17(10):105-107.
Design of Adaptive Fuzzy Controller for Nonlinear Systems
WU Haiqing, SU Zhan, SHEN Yuming
(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology,
Shanghai 200093, China)
AbstractIn this paper, a fuzzy adaptive controller is designed for the nonlinear system. The fuzzy adaptive controller is designed for the stability and control effect of the system based on the feedback control and the adaptive law of the parameter vector, combined with the Lyapunov stability theory. In order to verify the effectiveness of the controller, the controller is applied to the stability control of the two stage inverted pendulum system. The simulation results show that the controller is effective and has better control effect than the traditional control method.
Keywordsadaptive control; fuzzy control; Lyapunov stability theory; inverted pendulum
收稿日期:2015- 11- 11
作者简介:吴海晴(1991-),女,硕士研究生。研究方向:智能控制模糊控制等研究。苏湛(1983-),女,博士。研究方向:矩阵理论与应用等。
doi:10.16180/j.cnki.issn1007-7820.2016.07.011
中图分类号TP273+.2
文献标识码A
文章编号1007-7820(2016)07-036-04
