基于BP神经网络的表层悬浮物浓度预测模型

胡　田，　李贤哲，　于徐华

(中海环境科技(上海)股份有限公司，上海 200135)



基于BP神经网络的表层悬浮物浓度预测模型

胡田，李贤哲，于徐华

(中海环境科技(上海)股份有限公司，上海 200135)

摘要:悬浮物浓度是海洋沉积动力学领域中的重要参数，对其进行准确预测及定量研究绿潮爆发期间悬浮物所带来的影响具有重要意义。将BP(Back Propagation)神经网络应用于表层悬浮物浓度的预测中：将流速、水深、波高、温度、盐度及风速等影响悬浮物浓度的因素作为BP神经网络的输入单元，通过对苏北近岸海域进行调查，获取用于训练和预测的数据，建立表层悬浮物浓度的BP神经网络预测模型。将预测结果与多因子逐步回归拟合结果进行比较，得到逐步回归预测结果的平均相对误差为24.13%，BP神经网络预测结果的平均相对误差仅为13.02%。由此可见，BP神经网络预测结果具有更高的精度，可为苏北近岸海域表层悬浮物浓度的准确预测提供更可靠的途径。

关键词:BP神经网络；悬浮物浓度；苏北近岸海域；预测

0引言

研究近岸水体的悬浮物浓度及其通量，对认识海岸环境的演化规律，开发和持续利用港口、土地资源具有重要意义[1]。同时，悬浮物浓度作为决定水质浑浊度的主要因素，直接影响着海洋初级生产力、海水养殖及海洋渔业[2]。因此，快速、准确地监测悬浮物浓度具有十分重要的理论和实践意义。

传统的沿水深按层次采集水样或用浊度计单点测量获取悬浮物浓度的方法耗资巨大，数据不连续，空间分辨率低[3]；遥感方法测量悬浮物浓度具有监测范围广的优点，但其受同步监测资料不充分[4]、大气校正不彻底[5]及不同遥感数据不能简单套用相同的模式参数[6]等限制，反演精度较低。声学多普勒流速剖面仪(Acoustic Doppler Current Profilers ，ADCP)作为常规的测流仪器，其利用的散射体为水中的悬浮生物和悬浮沉积物[7]，因而具有测量悬浮物浓度的潜力。近年来，相关学者[8-10]围绕ADCP在悬浮物浓度测量方面的应用开展了广泛研究，取得了一些研究成果。但是，由于影响ADCP后向散射强度的因素(如回声强度、水温、盐度及水深等)众多，提取较为困难，且需要采集较多的水样进行标定，因此测量精度有待进一步提高。

人工神经网络是目前国际前沿研究领域应用的一门新兴交叉学科。近年来，国内外相关学者已将神经网络模型成功应用于水资源、水环境评价及水文时间序列等方面的研究中，拓宽了其应用领域，但将神经网络应用于悬浮物浓度预测的研究还较少。目前应用最多、研究较为成熟的是多层前馈网络误差反传算法模型，即BP(Back Propagation)模型。该模型是一种较特殊的非线性映射方法，通过一元函数的多次复合来逼近多元函数。BP神经网络模型具有处理复杂非线性函数的能力，因此这里以苏北近岸海域为例，利用BP神经网络建立苏北近岸海域表层悬浮物浓度的预测模型，以求准确、快速地获取该海域表层悬浮物的浓度数据。

1材料与方法

1.1影响因子确定与数据获取

在BP神经网络预测模型中，输入因子的选择对预测精度的影响很大。

1) 流速为悬浮物浓度的主要控制因素，研究结果表明：在底层流速达到临界起动速度后，底床泥沙会在剪切力的作用下发生再悬浮，在底层形成较大的悬浮物质量浓度水体；而在底层流速低于临界流速时，底层水体中的泥沙将慢慢落淤[11]。

2) 风通过波浪把能量传递给海水，在浅海水域对海底沉积物的起动和再悬浮有重要作用[12]。1983年，中美联合调查船在南黄海辐射沙洲区测量时突然遇到10级持续24 h的大风，海水表层悬浮物浓度随后增加了1倍，而底层则增加了6倍[13]，反映了风力对悬浮物浓度的重要影响。

3) 海水的温度与黏滞性成负相关关系，温度越低黏滞性越高，在降低悬浮颗粒沉降速度的同时，还使得相同流速的海水对海底的切应力增大，使得沉积物易于起动和再悬浮。

4) 波浪作用过程中，可使底层沉积物再悬浮，底床下部一定深度处的细粒沉积物会在渗流力的驱动下传输至表层，进而悬浮在水体中[14]。

5) 海水中的粗颗粒沉积物能在自身重力的作用下快速沉降至海底，而细颗粒物通常以絮凝的方式沉降，较高的盐度能促进细颗粒物的絮凝。

因此，选取流速、水深、波高、温度、盐度及风速作为影响悬浮物浓度的环境因子。

2012年8月和12月对布设于江苏近岸海域的3条断面的15个站点(见图1)进行了大面积调查。每个站点在每次调查中各采集1组流速、水深、波高、温度、盐度、风速及悬浮物浓度数据，共得到30组有效数据。

1) 流速和水深由安装全球定位系统(Global Positioning System，GPS)的ADCP(TRDI公司生产的WHRG-600KHz型)测得，测量时探头置于水下0.5 m处，并确保探头表面无杂物遮挡。

2) 温度和盐度由Seabrids37型温盐深仪 (Conductivity Temperature Depth，CTD)测得，测量前需提前在海水中感温2 min。

3) 风速由风速仪在四周无遮挡的船首测得，并取1 min的平均风速作为该站点的测量值。

4) 站点的波高数据通过目测获取，连续观测20次，将其平均值作为神经网络的输入变量。

5) 悬浮物水样按照《海洋监测规范》(GB 17378.3—2007)中的相关规定采集，在实验室用真空抽滤法获取：首先用预先在60 ℃下烘干的滤膜对水样进行过滤(为减小滤膜误差，采用双膜过滤过滤)，其次将附有泥沙的滤膜烘干、称重，最后计算得到悬浮物的浓度。

1.2BP人工神经网络模型

选取悬浮物浓度影响因子流速、水深、波高、温度、盐度及风速，建立基于BP神经网络的苏北近岸海域悬浮物浓度计算模型，BP神经网络结构示意见图2。

采用MATLAB 2013软件对BP人工神经网络模型进行设计，采用的神经网络模型为3层的反向传输神经网络，第1层为输入层，第2层为隐含层，第3层为输出层。各层的神经元之间形成连接，各层内的神经元之间没有连接。

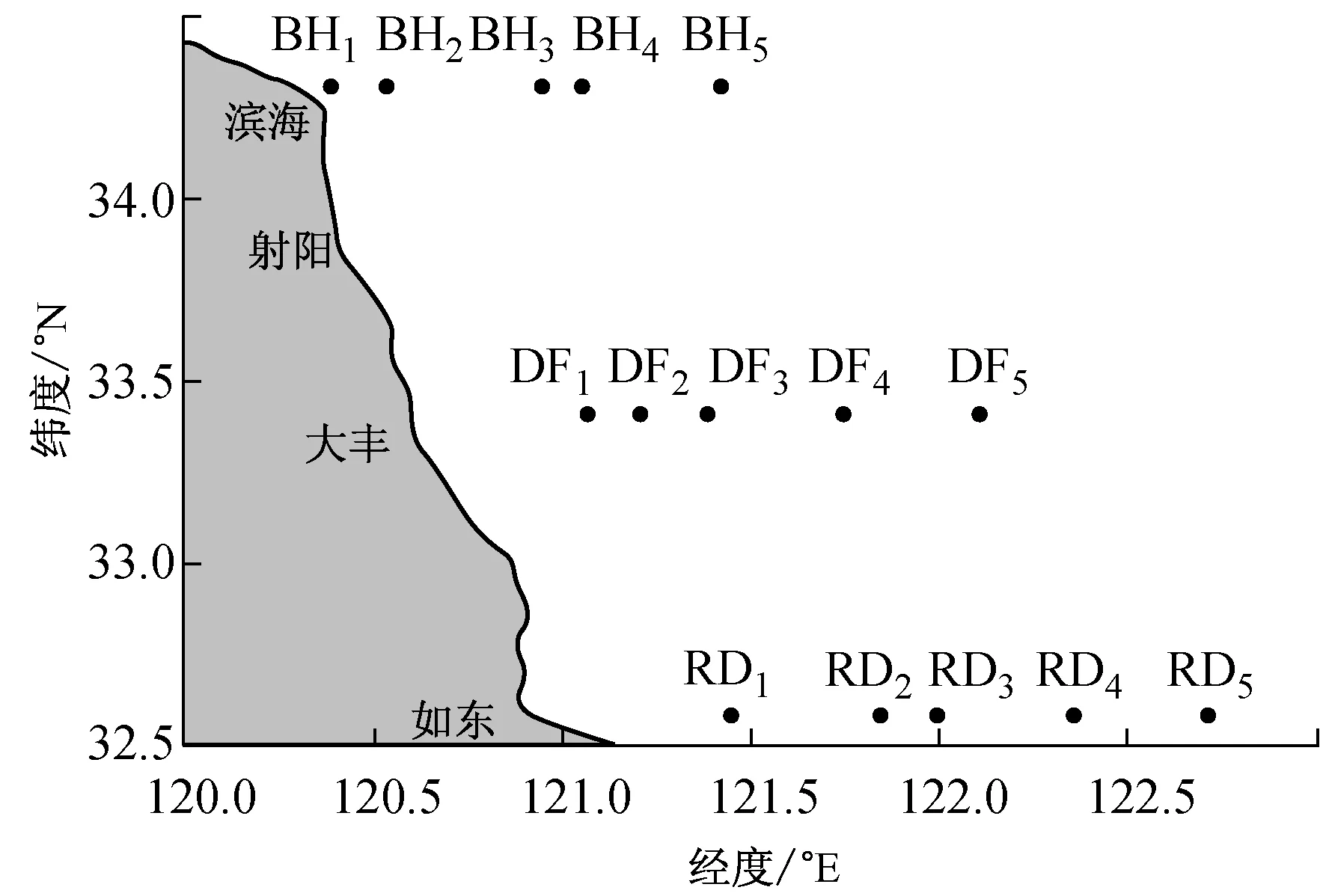
图1　调查海域站位分布图

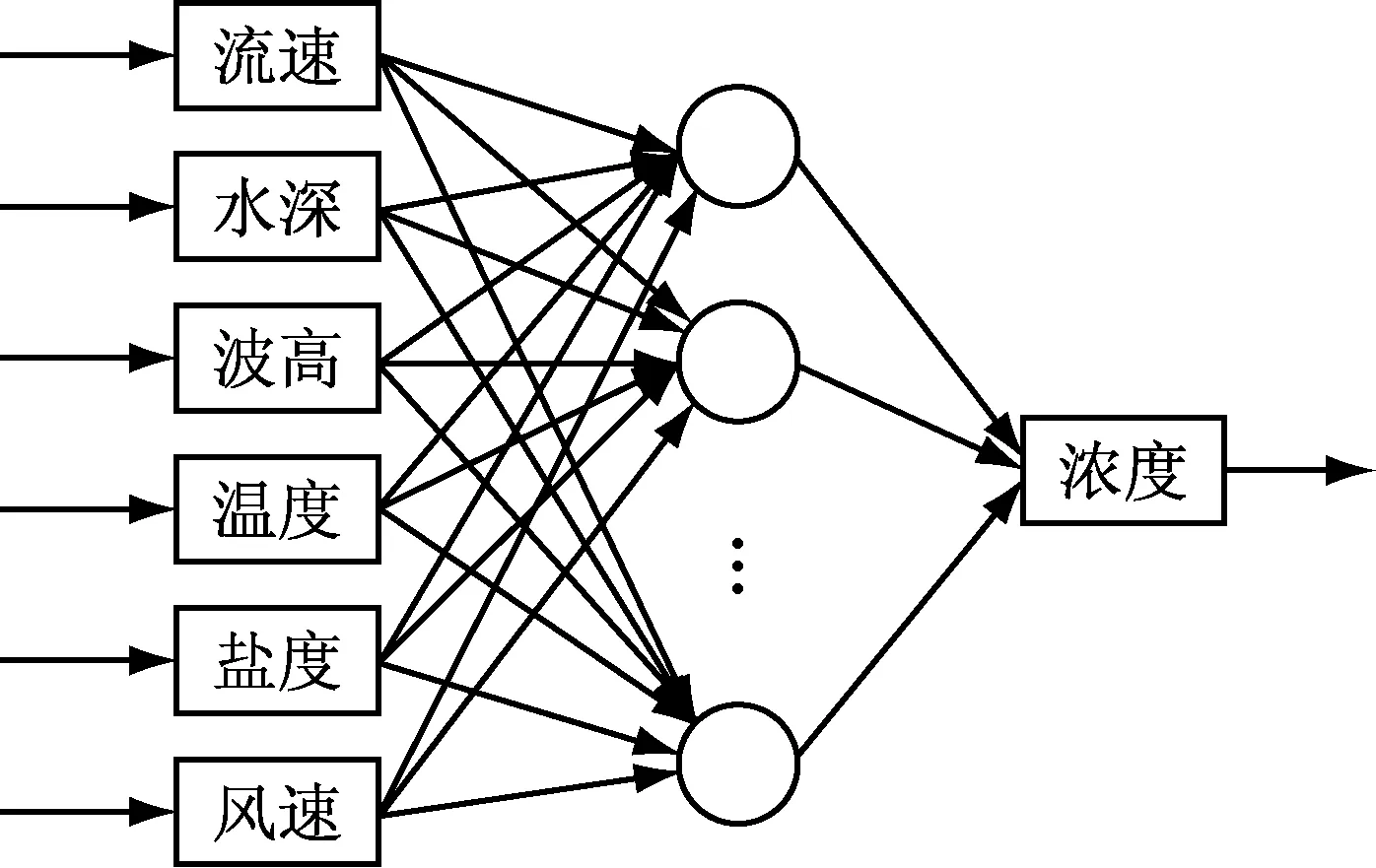
图2　BP人工神经网络结构示意

对于输入层神经元，为消除输入因子量纲不同对网络识别精度的影响，对输入变量进行归一化处理。

(1)

隐含层的神经元的输出为

(2)

(3)

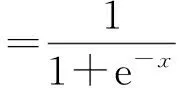
在对该网络进行训练时，会有若干组训练样本，每个样本均由输入和理想输出组成。当网络的所有实际输出与理想输出一致时，训练结束;否则，通过修改权重使网络的实际输出与理想输出一致。

在进行神经网络设计时，隐含层和输出层的传输函数分别为S型正切函数和S型对数函数。由于S型函数的极限值落在[0，1]内，因此进行网络训练时能快速地收敛，同时采用自适应的Levenberg-Marquardt快速学习算法训练网络。研究人员李伟[2]认为，样本集中80%的数据用作训练、20%的数据用作预测时网络性能稳定。在进行网络训练前，用Dixson异常值检验法(a≤0.05)剔除2组异常数据；随机选取剩余28组数据中80%的数据(约22组)作训练，剩余20%的数据(约6组)作检验，以使训练达到最佳效果[2]。期望误差值应通过对比训练确定，相对于隐含层神经元的数目，网络训练误差设置为0.000 1。

1.3多元线性回归模型

采用MATLAB 2013的regress函数建立多元线性回归模型，选用与BP神经网络模型相同的影响因子(流速、水深、波高、温度、盐度及风速)与BP人工神经网络模型进行比较。多元线性回归模型为

(4)

式(4)中：Xi为输入变量i的值；Y为实测悬浮物浓度；常数项b0和回归系数bi运用最小二乘法求得；εi为回归误差，回归求解的过程即为使平均误差ε最小的过程。

2结果与分析

2.1隐含层神经元数目的确定

BP网络隐含层神经元的个数需根据实际问题来确定[17]，这里通过计算样本模拟值与实测值之间的Pearson相关系数(R)的平方值和平均绝对百分误差(Mean Absolute Percentage Error, MAPE)来完成，平均绝对百分误差计算式为

(5)

表1为不同神经元数目下模型的预测结果。由表1可知，隐含层神经元为9时，BP网络对函数的逼近效果最好，相对误差最小。此外，网络的性能并非隐含层神经元的个数越多越好，当神经元个数增加到10时，误差反而增大。因此，这里构建的神经网络模型为6-9-1结构。图3为隐含层神经元为9时的网络训练示意图。由图3可知，模型经过6次训练就使误差降低到了目标误差。

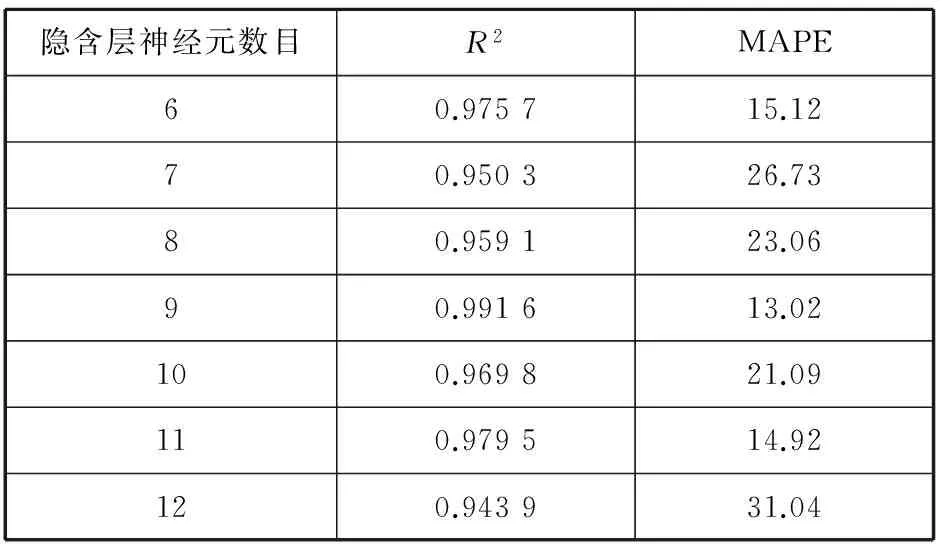
表1　不同神经元数目下模型的预测结果　%

图3　BP神经网络模型训练示意图

2.2多元线性回归系数的确定

利用数据处理系统(Data Processing System，DPS)操作平台对数据进行分析，将每个站点获得的流速、水深、波高、温度、盐度、风速及悬浮物浓度数据作为单个样本，不同站位获得的流速数据作为自变量，从而获得流速、水深、波高、温度、盐度及风速等变量，悬浮物浓度作为因变量放在最右边。将待分析的所有数据定义成数据矩阵列，进行逐步回归分析。

根据全部输入变量，运用逐步回归法得到悬浮物浓度ρ，多元线性回归预测模型为

ρ=1.110 1+0.061 9Vi-0.097 8Hi-0.113 0Li-0.514 0Ti-

0.951 2Si+0.128 9Vwi，i=1,2,3，…,22

(6)

式(6)中：ρ为悬浮物浓度；V为流速；H为水深；L为波高；T为表层水温度；S为盐度；Vw为风速。

2.3模型的验证

图4为人工神经网络模型与多元线性回归模型的拟合优度。从图4中可看出：当选择的隐含层神经元为9时，人工神经网络模型的拟合程度相比多元线性回归模型有很大提高；多元线性回归模型的悬浮物浓度拟合直线明显偏离期望值1∶1直线；人工神经网络模型的悬浮物浓度拟合直线与期望值1∶1直线较接近，拟合结果相比多元线性回归模型有很大提高。

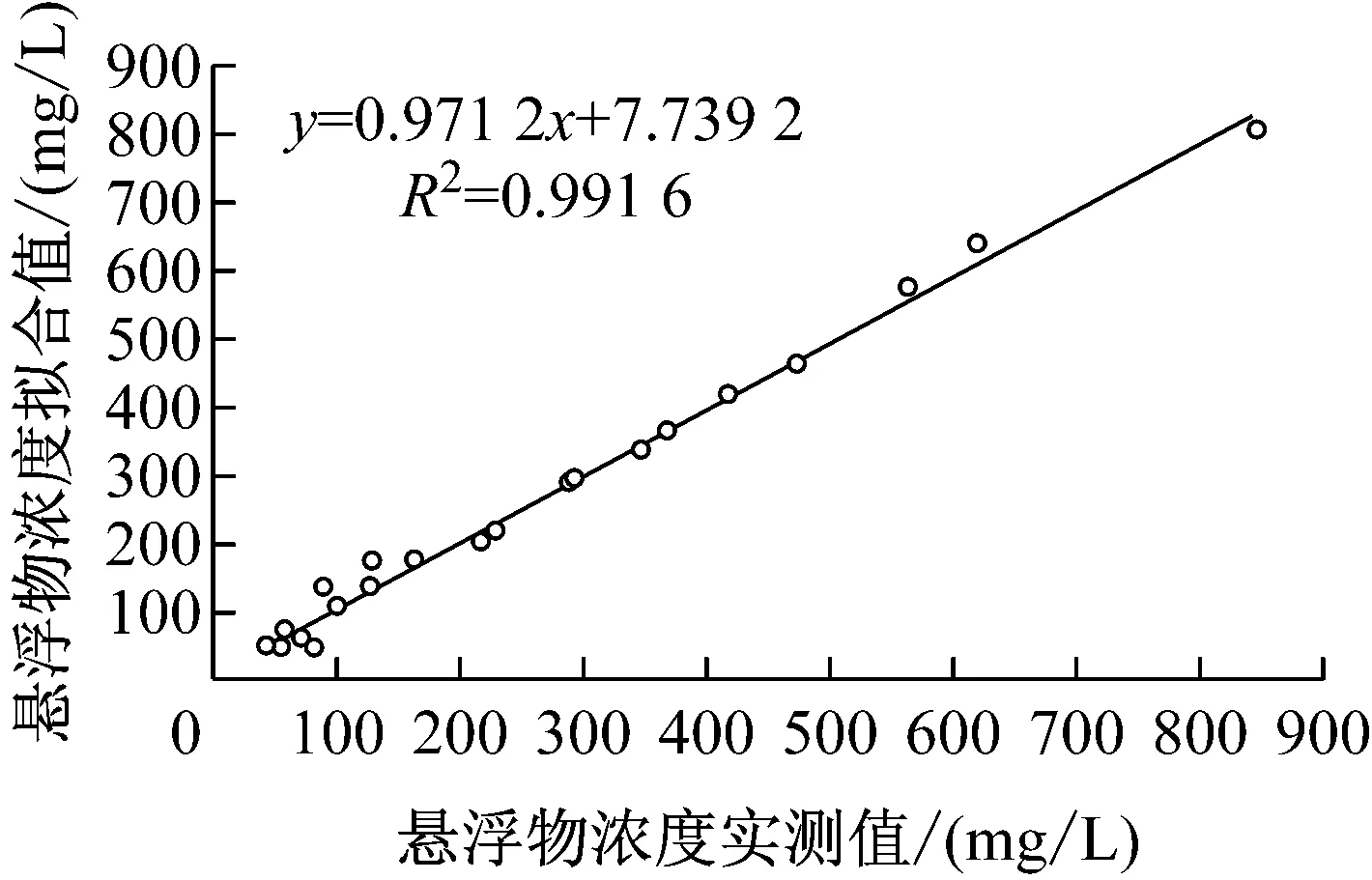
(a) 人工神经网络模型

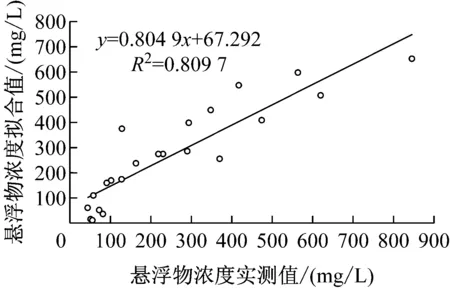
(b) 多元线性回归模型

为检验所建立的神经网络模型和多元线性回归模型的预测精度，选取剩余的6组数据对模型进行验证(见图5)。由图5可知，当隐含层神经元为9时，网络的MAPE仅为13.02%，与文献[18]中构建的BP神经网络模型的预测精度基本一致，相较多元线性回归的24.13%有较大幅度的提高。

3结语

以环境影响因子(流速、水深、波高、温度、盐度及风速)作为输入，悬浮物浓度作为输出，结合实测的悬浮物浓度，利用BP神经网络模型对江苏近岸海域的悬浮物浓度进行了研究。当隐含层神经元数为9个时，BP神经网络模型的训练效果最好，绝对百分误差仅为13.02%，而多元线性回归的绝对百分误差为24.13%。研究结果表明：BP神经网络能较准确地反演出江苏近岸海域悬浮物浓度，可用于揭示江苏近岸海域悬浮物浓度的空间分布规律，为研究悬浮物浓度对绿潮大规模发爆发的影响提供技术支撑。

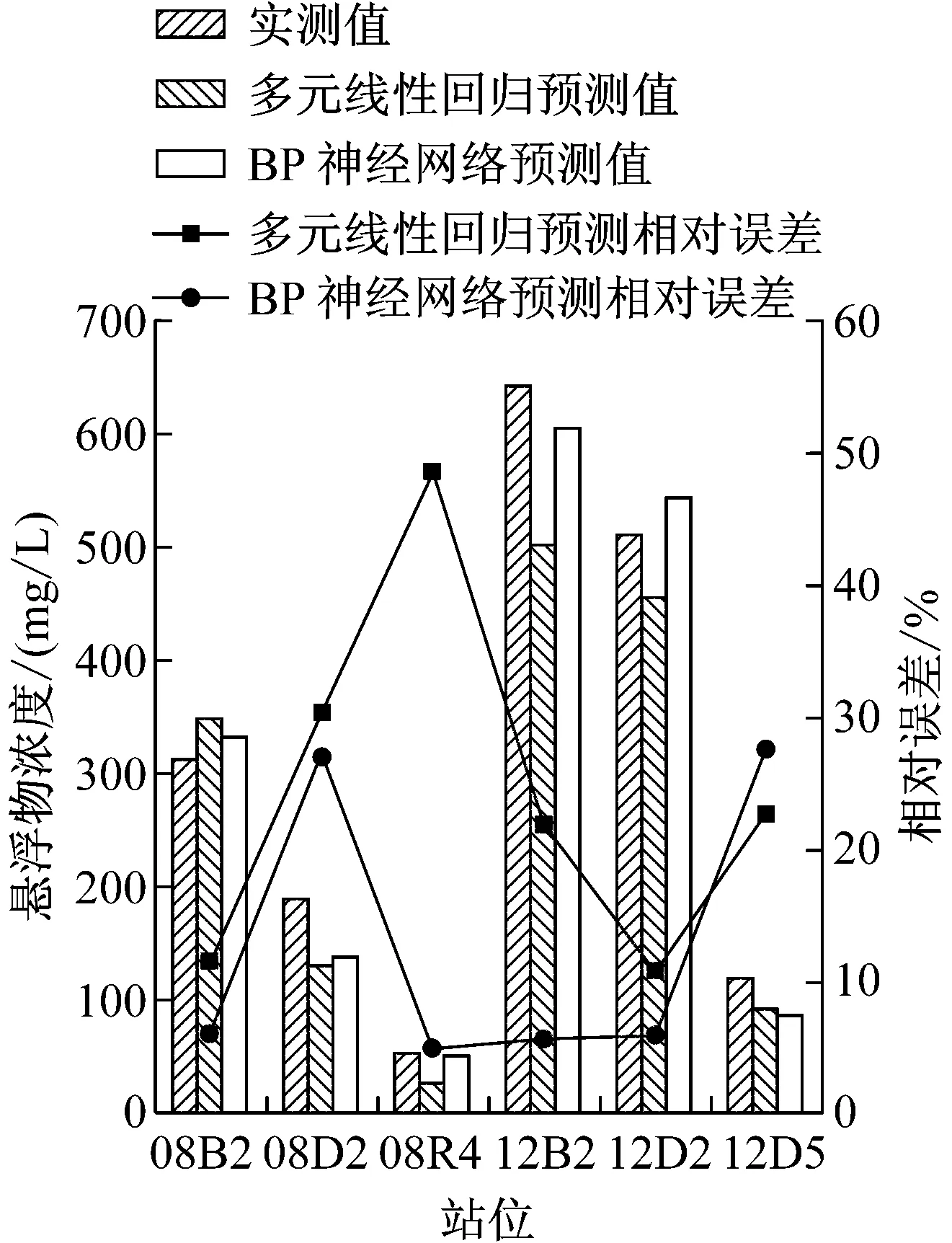
图5　BP神经网络与多元线性回归预测值和实测值对比

参考文献：

[1]汪亚平,高抒,李坤业.用ADCP进行走航式悬沙浓度测量的初步研究[J].海洋与湖沼,1999,30(6):758-763.

[2]李伟.人工神经网络方法反演东中国海悬移质浓度[J].海洋湖沼通报,2007(4):55-58.

[3]高建华,汪亚平,王爱军,等.ADCP在长江口悬沙输运观测中的应用[J].地理研究,2004,23(4):455-462.

[4]唐兆民,唐元春,何志刚,等.悬浮泥沙浓度的测量[J].中山大学研究生学刊(自然科学、医学版),2003,24(3):47-53.

[5]博克忖,荒川久幸,曾宪模.悬沙水体不同波段反射比的分布特征及悬沙量估算实验研究[J].海洋学报,1999,21(3):134-140.

[6]李四海,恽才兴.河口表层悬浮泥沙气象卫星遥感定量模式研究[J].遥感学报,2001,5(2):154-160.

[7]程鹏,高抒.ADCP测量悬沙浓度的可行性分析与现场标定[J].海洋与湖沼,2001,32(2):168-175.

[8]HOEKSTRA P， HOINTINK A J F.Observations of Suspended Sediment from ADCP and OBS Measurements in a Mud Dominated Environment[J].Coastal Engineering,2005(52):103-118.

[9]田慧娟,韩赋,朱柯行,等.基于多普勒声学原理测定海水悬沙质量浓度[J].淮海工学院学报(自然科学版),2013,22(2):89-92.

[10]孟令鹏.长江口悬沙输运观测中ADCP的应用[J].科技资讯,2012(3):89.

[11]陈斌,周良勇,刘健,等.废黄河口海域潮流动力与悬沙输运特征[J].海洋科学,2011,35(5):73-81.

[12]邢飞,汪亚平,高建华,等.江苏近岸海域悬沙浓度的时空分布特征[J].海洋与湖沼,2010,41(3):459-468.

[13]宋召军,黄海军,杜廷芹,等.南黄海辐射沙洲附近海域悬浮体的研究[J].海洋地质与第四纪地质,2006,26(6):19-25.

[14]郑杰文,贾永刚,刘晓磊,等.波浪作用下沉积物再悬浮过程研究进展[J].海洋地质与第四纪地质,2013,33(5):173-183.

[15]DANIEL M，HANES P T.A Review of Acoustic Measurement of Small-Scale Sediment Processes[J].Continetal Shelf Research,2001,22:603-632.

[16]李义天,李荣,黄伟.基于神经网络的水沙运动预报模型与回归模型比较及应用[J].泥沙研究,2001(1):30-37.

[17]孔德星,杨红.长江口区基于BP算法的表层悬沙浓度计算模型[J].海洋技术,2009,28(2):18-20.

[18]于东生,严以新,田淳.基于BP算法的泥沙含量预测研究[J].水运工程,2003(6):5-9.

Modeling with BP Neural Network for Predicting Suspended Solid Concentration in Surface

HUTian，LIXianzhe，YUXuhua

(China Shipping Environment Techlogy (Shanghai) Co., Ltd.， Shanghai 200135， China)

Abstract:Accurate prediction of suspended solid concentration is very important to quantitative study on the impact of the suspended solids during green tides. The BP neural network model for predicting suspended solid concentration surface is established and trained by the data acquired from SuBei Coastal Waters, with the input consisting of velocity, water depth, wave height, temperature, salinity and wind speed. Trials indicate that the relative error of the average prediction of the BP neural network is 13.02%, in contrast to 24.13% of that from the multi-factor stepwise regression.

Key words:BP neural network； suspended solid concentration； Subei coastal waters； prediction

收稿日期：2016-04-22

作者简介：胡田(1988—)，男，湖南岳阳人，硕士生，主要从事环境影响评价的工作。

文章编号：1674-5949(2016)02-0072-05

中图分类号：P734.23;TP183

文献标志码：A