全矢支持向量回归频谱预测方法

李凌均， 陈　超,2， 韩　捷， 陈　宏

(1.郑州大学 机械工程学院，河南 郑州450001；2.河南机电职业学院，河南.郑州451191)



全矢支持向量回归频谱预测方法

李凌均1， 陈超1,2， 韩捷1， 陈宏1

(1.郑州大学 机械工程学院，河南 郑州450001；2.河南机电职业学院，河南.郑州451191)

摘要：为了对机械设备进行故障类型和故障部位的准确预测，提出了全矢支持向量回归的频谱预测新方法.该方法使用全矢谱信息融合技术对同源双通道信号进行信息融合，采用支持向量回归对全矢谱特征参数进行预测，保证了训练数据信息的全面性以及预测结果的准确性.该方法对振动信号的频谱结构分布情况进行准确预测，从而为对机组的故障类型和故障部位预测奠定技术基础.通过对某1 000 MW汽轮机轴振进行频谱预测验证结果表明，该方法在对振动信号频谱结构特征进行预测方面具有较高的预测准确性.

关键词：全矢谱；支持向量回归；时间序列；频谱预测

0引言

对设备的振动规律及其发展趋势进行预测可以为故障的发生、发展，以及发生故障的类型、故障发生部位的预测提供基础[1].由于单通道的分析方法存在信息单一和信息利用不充分的缺点，而目前对旋转机械振动方面的预测基本限于通频振动幅值、峭度等统计指标的预测，无法对频谱结构和故障类型做出预测.文献[2-4]用不同的方法研究了机械设备故障发展变化和性能劣化的趋势，这些都是集中在对故障和劣化程度、以及剩余寿命的预测，却没有对频谱结构、故障类型和故障位置的预测.而同源信息融合的全矢谱技术就如在谐波轨迹的最大强度方向有一个虚拟探头在监测转子信号，保证了各谐波的最大强度[5]，使得对频谱进行预测变得有可行而有效.

文献[6-7]提出了基于同源信息融合的全矢谱技术，为单通道振动信号故障特征提取不完整而制约故障诊断结果可靠性和准确性提供了新的、有效的解决方法.文献[8-9]研究了基于全矢谱的高阶统计量特征提取对故障诊断的贡献,并将其应用于智能故障诊断中，取得了较好的效果.文献[10]对时间序列分析在工程中的应用进行了大量的研究，分析了时间序列模型在振动信号趋势预测的适用性.文献[11]将支持向量回归机应用于机械设备状态趋势预测，给出了具体的算法，表明支持向量回归机对机械设备的运行状态趋势具有较好的预测能力.文献[12-13]分别研究支持向量机预测方法在给水泵和风力发电机组中的故障预测中的应用.文献[14]将支持向量数据描述方法应用于设备故障程度的预测进行了细致深入的研究.

结合全矢谱技术及支持向量回归预测方法两者的优点，笔者提出了全矢支持向量回归的频谱(FVSVR)预测新方法.新方法使用全矢谱技术对同源双通道信号进行信息融合，采用支持向量回归对全矢谱特征参数进行预测，克服了单通道数据信息不完整的缺点，保证了训练数据信息的全面性以及预测结果的准确性.

1FVSVR频谱预测实现基础

1.1全矢谱技术

转子的涡动现象是各谐波频率下的组合作用，各谐波下的涡动轨迹是一椭圆.定义这些椭圆的长轴长度为振动强度评价的主振矢，短轴长度为振动强度的副振矢，转子在各谐波频率下的涡动强度是对故障诊断和识别的基本依据.

设转子同一截面内相互垂直方向同步采集到的两组振动数据序列为{xn}、{yn}，并得到离散的融合复序列{zn}={xn}+j{yn}，其中j2=-1， 对其作复傅里叶变化得到其频谱{Zn}.令

(1)

式中：RLk为椭圆的长半轴，表示振动的最大值,为主振矢；RSk为椭圆的短半轴，为副振矢.

1.2支持向量回归机算法

在线性回归问题中，对于给定的训练样本(xi,yi)，xi∈Rd，yi∈R，i=1，…，n，线性回归的目标就是求下列回归函数

f(x)=(w·xi)+b.

(2)

式中：w∈Rn；b∈R；(w·xi)为w与xi的内积，并且满足结构风险最小化原理.

(3)

式中:C为惩罚因子,是实现在经验风险和置信范围之间的折中;Remp为损失函数.常用的损失函数有Laplace函数、二次函数、Huber函数和ε-不敏感函数,其中ε-不敏感函数因具有较好的性质而得到广泛的应用,定义为

(4)

(5)

考虑可能超出精度的拟合误差,引入松弛因子,建立Lagrange方程,可求得线性回归函数:

(6)

对于非线性问题，根据V.Vapnik提出的核函数理论[15]，可以用核函数K(xi,xj)来替代内积运算，实现由低维空间到高维空间的映射，从而使低维空间的非线性问题转化为高维空间的线性问题.引入核函数后，相应的回归函数为如下形式:

(7)

常用的核函数有线性核函数、多项式核函数、高斯径向基核函数和指数径向基核函数.

1.3时间序列预测方法

假设系统的输出采样时间间隔是τ，得到的输出时间序列为

2.政府引导原则。在推动企业线上线下互动创新发展进程中，政府做到不过度干涉，更不越俎代庖，切实认清自身角色，找准着力部位，统一认识，加强引导，用总体规划、政策扶持、市场规范、公共采购等方式引导“+电子商务”重要资源向优势产业、优势企业集中，使政府真正成为促进线上线下互动创新发展的服务站、加油站和助推器。

x(0),x(τ),…,x(iτ),…,x((n-1)τ).

(8)

该输出序列也是对未来值进行预测时的输入序列.

由n时刻的前m个值预测第n个值的问题可表示为寻找如下的对应关系f的问题:

xn=f(xn-1,xn-2,…,xn-m).

(9)

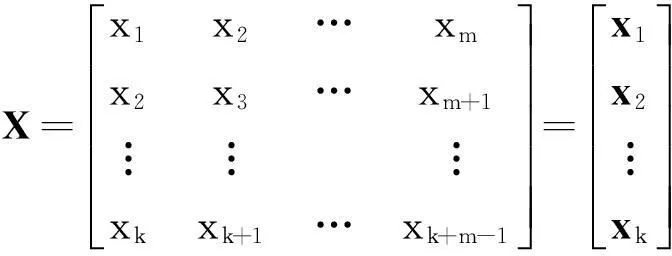
(10)

(11)

经过训练模型建立完成后，第1步预测的形式为

(12)

第2步预测的形式为

(13)

1.4预测精度的评价指标

选用平均相对误差评价指标来评价预测的效果，平均相对误差反映了预测值与真实值的偏离相对于真实值的大小，其计算公式为

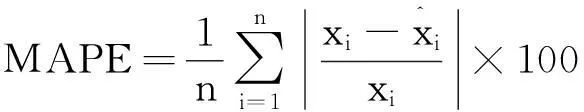
(14)

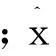
2全矢支持向量回归

①设在同一个截面上同步采集的两个相互垂直的信号为x(t)、y(t)；②将同源双通道信号x(t)、y(t)进行全矢谱同源信息融合；③确定回归步长，构建训练样本；④通过支持向量回归对训练样本进行模型训练；⑤进行预测，得到预测数据.

全矢支持向量回归的预测流程如图1所示.

图1　全矢支持向量回归的预测流程Fig.1　The prediction process of FVSVR

3实验分析及参数讨论

某电厂1 000MW汽轮机结构简图如图2所示.图2中每个滑动轴承处安装互相垂直的一对电涡流位移传感器来监测转子相对于轴承座的振动，即X和Y振动位移信号.转子转速为3 000r/min，按每周期32个点同步整周期采样(即采样频率为1 600Hz)，采样长度为1 024点.在长期的监测过程中发现高压转子2#轴承的轴振经常较大，易出现故障.对轴振X及轴振Y进行频谱分析及全矢谱分析，得到轴振X及轴振Y的频谱图及全矢幅值谱图，如图3所示.

图2　汽轮机结构简图Fig.2　The structure diagram of steam turbine

图3　#2轴承振动信号频谱图及全矢谱图Fig.3　The spectrum and full vector spectrum of the vibration signal of 2# bearing

从图3的对比可以看出，两个方向的频谱结构存在差异.分别对单通道的频谱进行预测，得到的预测结果可能会有不同的结论.而全矢谱保证了各谐波的最大强度，对其进行预测可以保证频谱结构的准确性，其结论也是唯一的.由于主振矢1×(1倍频)较大，此处对主振矢1×进行预测.每隔2h提取一组数据，连续提取48组，对其进行全矢谱信息融合，提取主振矢1×分量.分别将前24组数据，采用1.3节的数据组织形式构建训练样本，后24组数据作为预测样本.

预测模型的损失函数采用ε-不敏感函数，ε=1，惩罚因子C=200，核函数采用指数径向基核函数，其中宽度系数σ=10，回归步长m=5.图4显示的是对训练样本后面24个时刻的单步预测结果，相对平均误差为3.61%.

在预测过程中发现，惩罚因子C及指数径向基核函数的宽度系数σ对预测的影响很大，而C及σ并没有一个相对确定的值可以使预测效果更好.为了分析不同C及σ对预测效果的影响，进行大量的对比实验，预测精度的实验结果如图5所示.

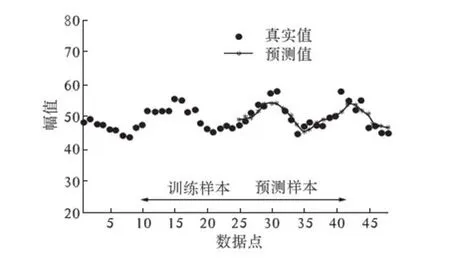
图4　主振矢1×单步预测结果Fig.4　The results of single step prediction of1× main vibration vectors

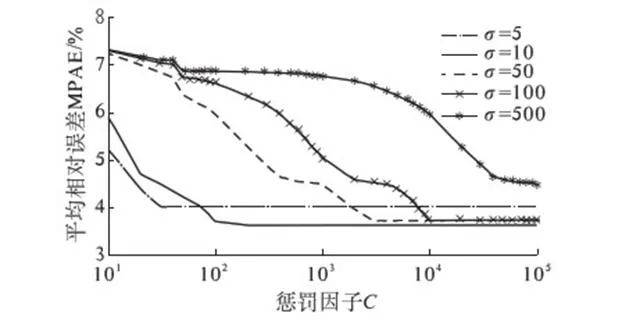
图5　惩罚因子C及宽度系数σ对预测误差的影响Fig.5　The influence on prediction error of C and σ

从图5可以发现，在不同宽度系数σ下，相对平均误差随着惩罚因子C的增大而降低，当惩罚因子C增大到一定程度时，误差趋于稳定.

C取不同值下的预测结果如图6所示.可以看出，在C较小时，预测曲线较为平缓，近似为直线；随着C增大，预测曲线的趋势渐渐地向着真实曲线的趋势发展，这就呈现出随着C的增大，预测误差随之降低.C的大小决定了由训练样本产生的经验风险对模型的影响的大小.如果C取值过小，会因为没有获得大量的训练数据，出现“欠学习”的现象，预测模型也就失去了预测能力；如果C取值过大，会出现“过学习”的现象，加大了建立模型的计算量.C应在能保证预测误差较小的前提下，取较小的值.

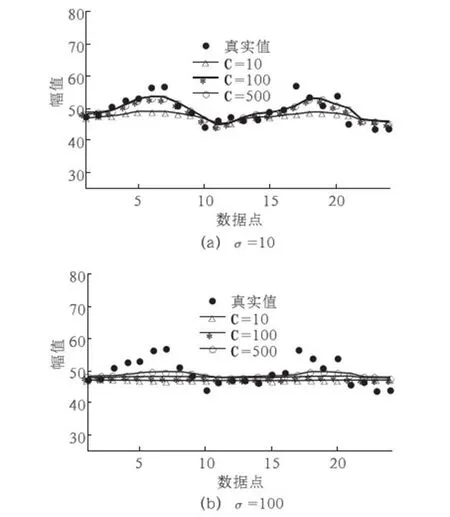
图6　C取不同值时的预测结果

Fig.6ThepredictionresultsofdifferentCvalues

另外，通过图6的对比还可以看出，当σ越大时，预测曲线随着C的增大，朝着真实曲线趋势变化的速度变得越来越慢，这也就是误差减小的速度越来越慢的原因.当σ选很大时，C需要相当大的值才能提高预测的精度.而C增加会使训练的迭代次数增加，降低训练的速度，所以σ不宜取的较大.一般情况下，可以对参数进行交叉寻优找到合适的宽度系数σ及惩罚因子C.

不敏感系数ε的取值也对模型的预测能力有一定的影响.表1是不同的不敏感系数ε下的单步预测平均相对误差.可以看出，本例中不敏感系数ε为1时，预测误差最小，这也是本例中不敏感系数ε选为1的原因.

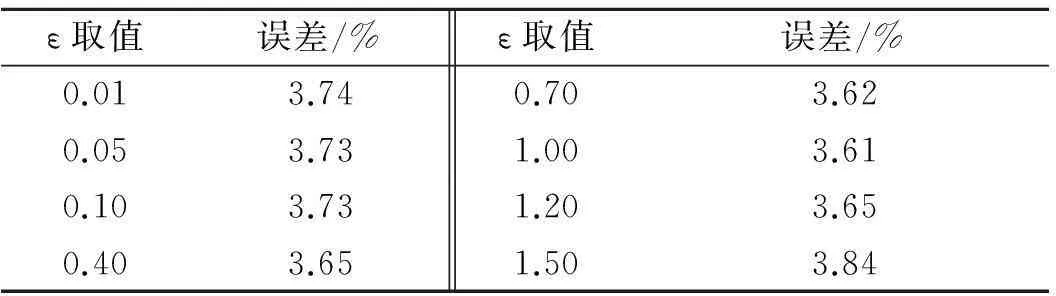
表1　ε取不同值时的预测误差

支持向量机预测模型中有多种核函数，选用不同核函数对预测效果的影响也有一定的影响.在研究过程中，分别采用了4种核函数进行了对比分析.表2给出了不同核函数的单步预测平均相对误差.其中，损失函数采用ε-不敏感函数，ε=1，惩罚因子C=200，指数径向基核函数宽度系数σ=10，多项式核函数的阶数d=3，Sigmoid核函数b=10，c=0.可以看出，在本样本中，指数径向基核函数预测效果较好.

表2　不同核函数时的预测误差

文献[13]中对支持向量回归中训练样本的回归步长m进行了研究.研究表明，m一般不宜过大，m过大并不能提高回归精度，但却增加了计算量，m=3～5时可得到较好的预测精度，选取回归步长m=5.

对主振矢1×进行多步预测(三步预测)，预测结果如图7所示.图中每个点都是三步预测结果中第3步的预测值，共22个第3步预测值，相对平均误差为4.22%.预测模型中的参数与单步预测的参数相同，即损失函数采用ε-不敏感函数，ε=1，惩罚因子C=200，核函数采用指数径向基核函数，宽度系数σ=10，回归步长m=5.可见，该方法对多步预测也有较好的预测效果.

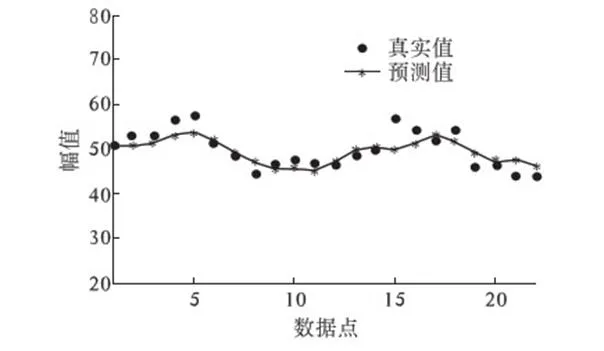
图7　主振矢1×三步预测结果Fig.7　The results of 3 steps prediction of 1× mainvibration vectors

4结论

为了更深入地研究旋转机械的状态趋势，提出了一种用全矢支持向量回归对旋转机械频谱预测的新方法.新方法使用全矢谱技术对同源双通道信号进行信息融合，保证了训练数据信息的全面性，避免了对单通道的频谱进行预测得到不全面或不正确的预测结果，并在单步及多步预测中具有较好的预测效果.在工程运用中，采用全矢支持向量回归方法建立的模型对转子振动频谱进行预测，通过预测结果可以对机组未来的情况进行深入全面的分析，判断振动增大的内在原因，尽早对状态不良的机组进行针对性较强的处理措施，避免机组发生意外事故及经济损失，提高了机组运行的安全性，具有较强的工程应用意义.

参考文献：

[1]何正嘉, 陈进, 王太勇,等.机械故障诊断理论及应用[M]. 北京：高等教育出版社, 2010.

[2]李巍华,李静,张绍辉.连续隐半马尔科夫模型在轴承性能退化评估中的应用[J].振动工程学报, 2014, 27(8):613-620.

[3]李永耀，韩捷，管腾飞，等.全矢AR-Kalman滤波的机械故障趋势预测方法研究[J].机械设计与制造，2015(1)：217-219.

[4]BOKOSKIP，GAPERINM，PETELIND.BearingfaultprognosticsbasedonsignalcomplexityandGaussianprocessmodels[C]//2012IEEEInternationalConferenceonPrognosticsandHealthManagement.Denver,CO,USA;IEEEPress,2012:1-8.

[5]韩捷, 巩晓赟, 雷文平. 面向旋转机械的虚拟融合检测技术研究[J]. 振动与冲击, 2012, 31(s)：120-123.

[6]韩捷, 关惠玲, 梁川,等. 矢谱：一种实用的旋转机械故障诊断分析方法[J]. 机械强度, 1998, 20(3)：212-215.

[7]韩捷. 全矢谱技术及设备故障诊断应用研究[D].上海：同济大学机械学院, 2005.

[8]李凌均，韩捷，李朋勇,等.基于矢双谱的智能故障诊断方法[J].机械工程学报,2011,47(11):64-68.

[9]李凌均, 韩捷，李朋勇,等.矢双谱分析及其在机械故障诊断中的应用[J].机械工程学报,2011,47(17):50-54.

[10]杨叔子, 吴雅, 轩建平.时间序列分析的工程应用[M]. 2版：上，武汉：华中科技大学出版社, 2007.

[11]李凌均, 张周锁, 何正嘉. 基于支持向量机的机械设备状态趋势预测研究[J]. 西安交通大学学报, 2004, 38(3)：230-233.

[12]叶兆青，卢坤杰，林光营,等. 基于支持向量机的给水泵故障预测研究[J].锅炉制造，2014(4):41-45.

[13]胡庆春. 基于支持向量机和统计过程控制的风电机组故障预测算法的研究[D].北京:华北电力大学机电学院,2011.

[14]陈斌,阎兆立,程晓斌. 基于DVDD和相对距离的设备故障程度预测[J].仪器仪表学报，2011,32(7)：1558～1563.

[15]VAPNIKVN.Thenatureofstatisticallearningtheory[M].NewYork：Springer, 1995.

The Prediction Method of Frequency Spectrum Based onFullVectorSupportVectorRegression

LI Lingjun1, CHEN Chao1,2, HAN Jie1, CHEN Hong1

(1.Research Institute of Vibration Engineering, Zhengzhou University, Zhengzhou 450001, China;2.Henan Mechanical andElectricalVocationalCollege,Zhengzhou451191,China)

Abstract:In order to predict the fault type and the fault position of rotating machinery more accurately, a new prediction method of frequency spectrum based on full vector support vector regression is proposed. The new method uses the full vector spectrum technology to merge the homologous double channel signal information, and uses support vector regression to predict the full vector spectrum characteristic parameters, which can ensure the comprehensiveness of the training data and the accuracy of predict result. This method can forecast the frequency spectrum of the vibration signal accuracy and can then give the technical based for fault type and fault position predict. The experimental results of the frequency spectrum forecast of a 1000 MW steam turbine shaft show that this method can predict fully and accurately the spectrum’s structure of vibration signal.

Key words:full vector spectrum; support vector regression; time series; frequency spectrum prediction

收稿日期:2015-10-19；

修订日期：2015-11-20

基金项目:国家自然科学基金资助项目(50675209)

作者简介:李凌均(1964—)，男，河南南阳人，郑州大学副教授，博士，主要从事机械故障诊断研究，E-mail:lingjun@zzu.edu.cn.

文章编号:1671-6833(2016)03-0078-05

中图分类号：TH17

文献标志码：A

doi:10.10375/j.issn.1671-6833.2016.03.018