钢-砼混合梁斜拉桥的颤抖振时域分析

李　宇，李　钊，李　琛

(1.长安大学 旧桥检测与加固技术交通行业重点试验室, 陕西 西安 710064；2.长安大学 建筑学院, 陕西 西安 710064)



钢-砼混合梁斜拉桥的颤抖振时域分析

李宇1，李钊1，李琛2

(1.长安大学 旧桥检测与加固技术交通行业重点试验室, 陕西 西安 710064；2.长安大学 建筑学院, 陕西 西安 710064)

摘要：以大跨钢-砼混合梁斜拉桥为研究对象，利用三次拉格朗日多项式插值的改进谐波合成法模拟了大桥所处场地的脉动风荷载.在此基础上，采用ANSYS建立了大跨斜拉桥的有限元模型，并利用ANSYS的APDL语言进行了二次开发，编制了能够计算钢-砼混合梁斜拉桥颤抖振响应的程序.研究结果表明：大跨钢-砼混合梁斜拉桥的颤抖振响应不仅会引起桥梁疲劳振动，进而降低桥梁构件的使用寿命，而且会危及施工人员和机械的安全，影响成桥运营后的行人舒适性和高速行车的安全性.

关键词：斜拉桥；颤振；抖振；非线性；时域分析

0引言

随着我国桥梁工程建设的迅猛发展，许多大跨径的斜拉桥得以建成，而它们的风致振动问题——特别是颤抖振响应，也成为工程界研究的热点.项海帆等[1]阐述了特大跨度桥梁抗风研究的新进展；李永乐等[2]对桥梁抖振时域和频域分析的一致性进行了研究；韩万水等[3]对大跨度斜拉桥抖振时域分析进行了理论实例验证及影响因素分析；张志田等[4]、DEODATIS等[5]进行了基于气动新模型的大跨度桥梁的频域抖振分析；马麟等[6]采用改进谐波合成法对杭州湾跨海大桥风场进行了模拟；王中文等[7]对钢桥塔裸塔状态涡激振动和斜拉索的风致振动进行了减振方法的研究；CHEN等[8]、DAVENPORT等[9]等国外学者也对大跨桥梁的抖振响应进行研究；袁小钦等[10]研究了MR-TMD减振系统，并探讨了该系统在连续箱梁桥振动控制中的作用效果；宫成等[11]以施工期间的高墩大跨斜拉桥为研究对象，研究了控制结构风致振动的措施；唐启等[12]针对分幅式斜拉桥施工期抗风措施展开研究，并提出了对应的制振措施.笔者以钢-砼混合梁斜拉桥为工程背景，利用ANSYS参数化设计语言(APDL)编制了计算程序，对大跨桥梁进行了颤抖振时域分析.

1基本理论

作用于大跨桥梁上的外荷载等效节点力为：

Fb(t)=Fbg+Fstb+Fbub+Fseb.

(1)

式中：Fbg为桥梁自重；Fstb为静风荷载；Fbub为抖振荷载；Fseb为结构自激力.假设在风荷载作用下，桥梁静止不动，此时的定常反应[1]为风静力作用Fstb.风轴坐标下的静力三分力为

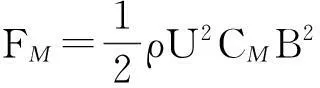
(2)

式中：FD、FL、FM为阻力、升力和扭矩；CD、CL、CM为FD、FL、FM的系数；A、B为主梁投影高度和宽度；ρ为大气密度；U为平均风速.

引入气动导纳后，抖振力Fbub可表示为

(3a)

(3b)

(3c)

(4)

2建立有限元模型

澜沧江大桥主桥为双塔三跨双索面钢-砼混合梁斜拉桥，总长700m，桥宽26m，跨径布置150m+400m+150m.主跨采用‘π’形钢-混凝土组合梁，边跨采用预应力混凝土加劲梁.用ANSYS建立了图1的有限元模型，步骤如下：①用Beam4梁单元模拟加劲梁、主塔、辅助墩、过渡墩、刚臂等，其中加劲梁采用刚度和质量一致的等代方法，即先计算出钢-混凝土组合梁的截面特性，可得到截面的两个方向的抗弯惯性矩、自身抗扭惯性矩以及等效面积，然后以实参数的形式赋予Beam4单元；②用Link10单元模拟斜拉索；③用MASS21质量单元模拟防撞护栏、检修道护栏、桥面铺装、横隔梁等质量及质量惯性矩；④定义x、y、z为顺桥、竖桥和横桥向.主要振型频率及等效质量如表1和图2～3所示.

表1　主要自振频率及等效质量

图1　有限元模型Fig.1　FEA model

图2　第2阶振型Fig.2　Modal 2

图3　第5阶振型Fig.3　Modal 5

3模拟脉动风场

采用改进谐波合成法[6]模拟脉动风场，并考虑Davenport相关函数修正脉动风沿桥轴的空间效果，以Simiu谱(横向)和Panofsky谱(竖向)为目标谱，用MATLAB编程对主梁、桥塔、过渡墩及辅助墩的横向和竖向脉动风场进行模拟(基本参数见表2).图4～5给出桥梁关键点的横桥与竖桥向风速时程及它们功率谱和目标功率谱的对比，可知：模拟的功率谱与目标功率谱吻合理想，即模拟的风场可作为抖振计算使用.

表2　风场模拟基本参数表

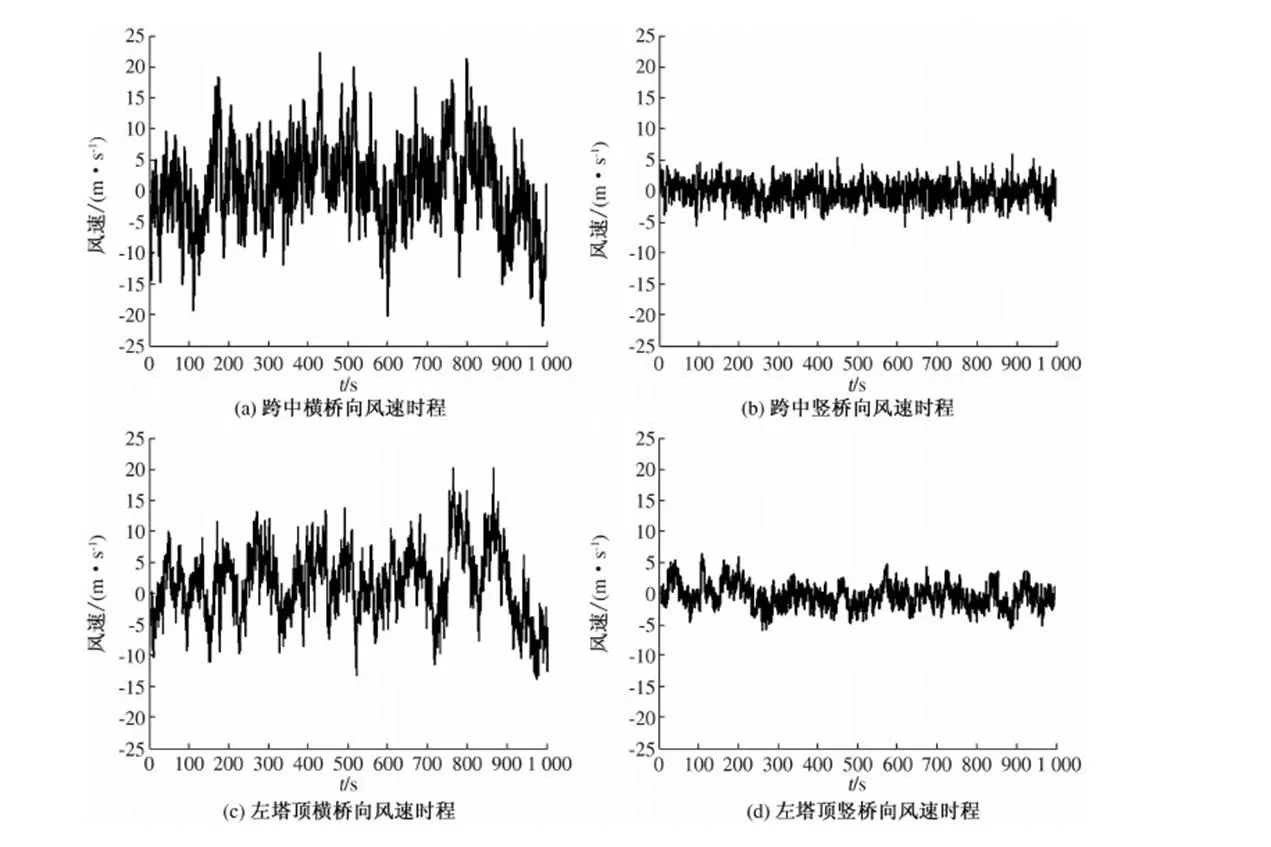
图4　各关键点脉动风速时程Fig.4　Turbulent wind speed of several critical point

图5　脉动风速模拟风功率谱和目标功率谱Fig.5　Wind power spectrum and target spectrum of turbulent wind speed

4计算结果分析

笔者综合考虑桥梁自重、静风荷载非线性、Davenport准定常抖振力、Scanlan自激力、结构阻尼等，编制了基于ANSYS软件的APDL参数化设计语言，实现了大跨斜拉桥的三维非线性抖振时域分析.对该桥成桥状态初始设计方案进行了0°风攻角和设计基准风速下的风荷载响应分析，并给出主梁和主塔上多个控制截面的风荷载位移和内力响应.其中，位移与坐标轴同向为正，反之为负；内力方向依赖计算风向，由于计算风向存在相向变化，因而内力正负号无实际意义.图6给出了主梁沿跨度表示的3个方向上的位移RMS值.图7给出了主梁跨中的3个方向上的位移时程曲线.图8给出了左主塔底部的弯矩时程曲线.从图7可知：①抖振属于风致限幅振动响应，一般不引起大跨桥梁灾难性损坏，但由于抖振发生频率较高，将会引起大跨桥梁的疲劳振动，进而导致大跨桥梁局部构件寿命的缩短；②过大的抖振响应会使大跨桥梁施工期间的振动，进而危及施工人员的安全和施工机械的使用，而且也会影响大跨桥梁成桥运营后的行人舒适性和高速行车的安全性.

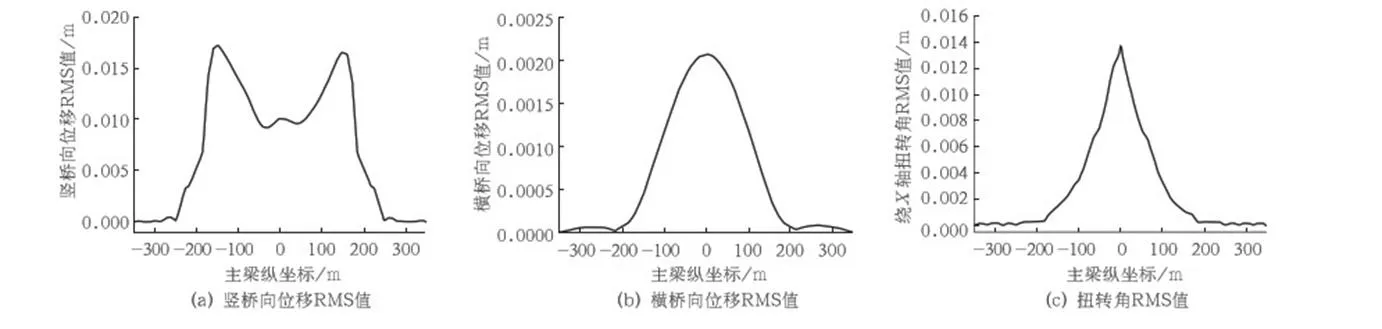
图6　主梁沿跨向位移RMS值Fig.6　RMS of displacement along main beam

图7　主梁跨中位移时程Fig.7　Time-history displacement of mid-span

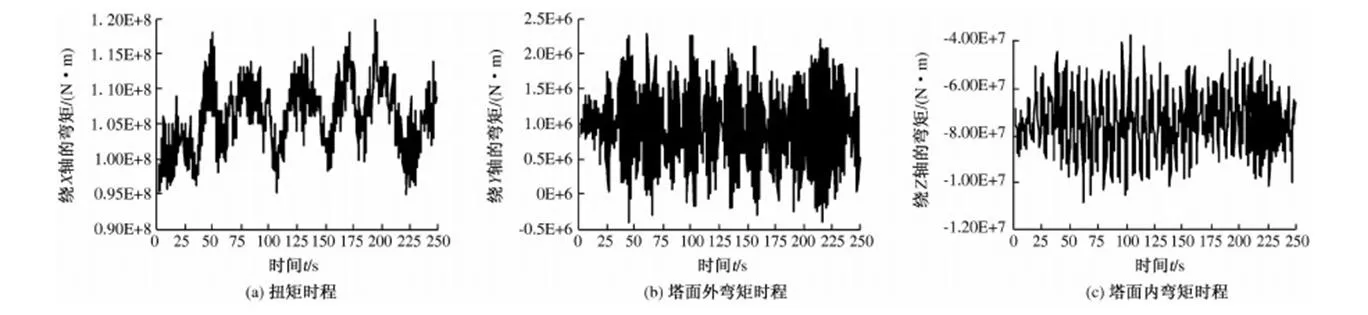
图8　左主塔底部弯矩时程Fig.8　Time-history moment at the bottom of left tower

5结束语

以澜沧江大桥为工程背景，利用三次拉格朗日多项式插值的改进谐波合成法对大桥所处场地的脉动风荷载时程进行模拟，并利用ANSYS的APDL语言进行了二次开发，编制了能够计算钢-砼混合梁斜拉桥颤抖振响应的程序，并对其进行了研究，从中可知：大跨斜拉桥抖振位移的最大值发生在桥梁的不同位置——最大横桥向和扭转变形抖振响应都发生于跨中，而最大纵向位移抖振响应则发生于1/3和2/3跨.由此可见，大跨钢-砼混合梁斜拉桥的颤抖振响应会引起桥梁疲劳振动，进而降低桥梁构件的使用寿命，而且会危及施工人员和机械的安全，影响成桥运营后的行人舒适性和高速行车的安全性.

参考文献：

[1]项海帆, 陈艾荣. 特大跨度桥梁抗风研究的新进展[J]. 土木工程学报, 2003, 36(4): 1-8.

[2]李永乐, 廖海黎, 强士中. 桥梁抖振时域和频域分析的一致性研究[J]. 工程力学, 2005, 22(2): 179-183.

[3]韩万水, 陈艾荣, 胡晓论. 大跨度斜拉桥抖振时域分析理论实例验证及影响因素分析[J]. 土木工程学报, 2006, 39(6): 66-71.

[4]张志田, 葛耀君, 陈政清. 基于气动新模型的大跨度桥梁频域抖振分析[J]. 工程力学, 2006, 23(6): 94-101.

[5]DEODATISG.Simulationofergodicmultivariatestochasticprocesses[J].Journalofengineeringmechanics, 1996，122(8):778-787.

[6]马麟, 刘健新, 韩万水. 基于改进谐波合成法的杭州湾跨海大桥风场模拟研究[J]. 郑州大学学报(工学版), 2008, 29(1):56-60.

[7]王中文, 朱宏平, 廖海黎，等. 钢桥塔裸塔状态涡激振动的TLD减振方法研究[J]. 华中科技大学学报(城市科学版), 2009, 26(2): 9-11.

[8]CHENX，MATSUMOTOM，KAREEMA.Aeradynamiccoupledeffectsonflutterandbuffetingofbridges[J].Journalofengineeringmechcmics,2000,126(1):17-26.

[9]DAVENPORTAG.Buffetingofasuspensionbridgebystormwinds[J].Journalofthestructuraldivision, 1962, 88(3): 233-270.

[10]袁小钦, 刘习军, 张素侠.MR-TMD减振系统对连续箱梁桥振动控制研究[J]. 振动与冲击, 2012, 31(20): 153-158.

[11]宫成, 刘志文, 谢钢,等. 高墩大跨斜拉桥悬臂施工期风致振动控制[J]. 工程力学, 2015, 32(增刊): 122-128.

[12]唐启, 李鑫, 游新鹏,等. 基于抖振分析的分幅式斜拉桥施工期抗风措施研究[J]. 中国港湾建设, 2015, 35(6): 20-25.

Flutter and Buffeting Analysis for Cable-stayed Bridge with Steel-concrete Girder

LI Yu1， LI Zhao1， LI Chen2

(1.Key Laboratory of Ministry of Communications for Bridge Detection & Reinforcement Technology, School of Highway, Chang’an University, Xi’an 710064, China； 2.School of Architecture, Chang’an University, Xi’an 710064, China)

Abstract:Based on long-span and steel-concrete bridge, the perfect stochastic fluctuating wind field process is generated to simulate stochastic wind loads by using improved WAWS method. Then, the FEA model of long-span cable-stayed bridge is established by using ANSYS. Based on ANSYS parametric design language, one calculation program is prepared to calculate the flutter and buffeting analysis for cable-stayed bridge with steel-concrete composite girder. Some meaningful conclusions are drawn that flutter and buffeting would cause vibration fatigue to reduce the lifetime of bridge members and endanger the safety of builders and machines. And, flutter and buffeting also have bad effects on pedestrian comfort and the security of high-speed road. Some meaningful references, which are used to calculate flutter and buffeting of long-span and steel-concrete bridges, are provided for further research on wind-induced vibration for long-span bridges.

Key words:cable-stayed bridge; fluttering response; buffeting response; nonlinear; time domain analysis

收稿日期:2015-09-30；

修订日期：2015-11-19

基金项目：国家自然科学基金资助项目(51408042)；陕西省自然科学基金资助项目(2014JQ7253)

作者简介:李宇(1982—)，男，福建福州人，长安大学副教授，博士后，主要从事桥梁抗震及抗风研究，E-mail: liyu@chd.edu.cn.

文章编号:1671-6833(2016)03-0069-05

中图分类号：U442.5

文献标志码：A

doi:10.13705/j.issn.1671-6833.2016.03.016