绝缘子预期电荷Q50的计算

孙长海，王　明，吴　彦，马海峰，葛恒序，赵伟程，陈百通

(1. 大连理工大学电气工程学院，辽宁 大连　116023；2. 国网鹤岗供电公司，黑龙江　鹤岗　154101；3. 国网大连供电公司，辽宁 大连116001)



绝缘子预期电荷Q50的计算

孙长海1，王明1，吴彦1，马海峰2，葛恒序3，赵伟程1，陈百通1

(1. 大连理工大学电气工程学院，辽宁 大连116023；2. 国网鹤岗供电公司，黑龙江鹤岗154101；3. 国网大连供电公司，辽宁 大连116001)

摘要绝缘子作为电力系统的重要部件，当长期在直流环境工作时，其绝缘内部将发生离子迁移，致使其绝缘性能降低，严重时会引发电力系统故障。因此，绝缘子出厂产品需要通过老化试验等一系列试验验证其绝缘性能，在此之前，需要计算其预期电荷量。该文针对现有标准绝缘子预期电荷计算公式值得探讨之处，重新基于微积分原理分析了绝缘子预期电荷量的定义与计算公式，提出了基于Matlab的数值计算方法，并进行了验证，得到了一组绝缘子预期电荷量较为精确的计算结果，为后续绝缘子老化机理的进一步理论分析和老化试验提供了重要参考。

关键词绝缘子；预期电荷；老化时间；数值计算

绝缘子是电力系统的重要部件，其产品出厂时应检验合格性。GB/T19443-2004规定的直流系统用盘式瓷绝缘子，出厂验收时需按标准做离子迁移试验[1]。离子迁移是指直流电压下，绝缘子电介质中Na+和K+离子向阴极的迁移，会导致绝缘子电气和机械性能的变化。离子迁移试验需要用通过绝缘子的电荷来表征。预期电荷 是指在预期50年期间在参考大气条件和所施电压下，通过绝缘子的全部电荷量[1]。这个电荷量也可以在短时间内达到，需要对绝缘子施加高温和高压，并耐受一段时间，来加速其老化。之后其泄漏电流以及耐压特性可以用来评估该绝缘子在预期工作寿命内的质量。在老化实验之前，要得出老化试验的时长，这就需要先计算出绝缘子的预期电荷 。

目前对绝缘子离子迁移试验已开展了一定研究。文献[2]较早研究了直流线路盘形悬式绝缘子的失效机理和可靠性验证试验。文献[3]建立了直流电场下绝缘子微观碱金属双离子迁移模型。文献[4]对不同工作环境下的绝缘子进行有限元建模仿真，得到了相应电场电位的分布。文献[5]对大量的绝缘子离子迁移的试验过程方法进行了总结。文献[6]通过3种微观性能测试方法对多支在役绝缘子的微观性能进行测试分析，初步建立了 110kV电压等级复合绝缘子微观运行性能评估模型。文献[7]在研究大量试验的基础上，软硬件结合，研发了一套绝缘子离子迁移试验的试验系统。文献[8]对非常规绝缘材料的表面特性进行了研究。文献[9]详细研究了交流复合绝缘子的不同工作环境下的环境参数对绝缘子绝缘性能参数对的影响。

国内对绝缘子离子迁移试验预期电荷计算的研究尚属空白。本文通过对现有标准中预期电荷计算公式的研究，结合Matlab计算程序，实现了一种较为精确的预期电荷计算方法。

1现有公式的探讨

标准中规定[1]，在一定工作电压下的预期电荷为：

式中：Ut为绝缘子工作电压；t(θ)为某一温度的工作时长；R(θ)为某一温度的绝缘子体电阻。

这里希望在-15～65℃温度范围内，取若干个离散的温度值θ1，θ2，…，θn，计算出各个温度的累积电荷量，再将各个温度的累积电荷量求和以得到整个温度范围内的总累积电荷量。

2修正后的数值计算公式

想解决上面的问题，需要注意区间离散划分求和的原则，即得到离散点后应乘以各自离散区间后再求和。参考高等数学中关于定积分的定义，在原公式末尾加入相邻离散温度的区间长度θ，式(1)修正为：

若将温度[θ1θ2]区间进行n等分，则区间长度为：

第n区间起点的温度值为：

θhn=θ1+(n-1)Δθ(4)

参照标准中的定义，某一离散温度点绝缘子的工作时长和体电阻分别为：

则式(2)离散化的形式为：

(7)

式(7)即为绝缘子预期电荷的数值计算公式。

3基于MATLAB的算法

至此，不难用Matlab实现上述绝缘子预期电荷量和老化试验天数的数值计算，来测试本文的论述。基于Matlab的程序如下：

M=25;

sigma=10;

theta1=M+4*sigma;

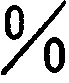
theta=(theta0:step:theta1-step);

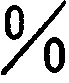
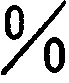
A=6.0046e3;

tp=exp(-(theta-M).^2/(2*(sigma^2)))/

(sigma*(sqrt(2*pi)));

t0=50*365*24*3600;

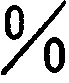
R=R130*exp(A/(273+theta))/

若裂隙研究区域内有N个节点(裂隙交叉点)，M个线单元(交叉点之间的裂隙段)，则可以组成N个形式为(1)的方程，写成矩阵形式为：

exp(A/(273+130));

R130=1.452e12;

下面对程序作2点说明。

1)绝缘子工作环境的温度theta，理论上取值范围为正负无穷，实际应用中应该为-15～65℃。这里为保证精度，能在正态分布中取到可能多的点且也不至过多，取了均值两侧正负4倍标准差的范围。实际上从后面的测试结果可以看到，[M-4sigma，M+4sigma]范围内正态分布之和已经很接近于1了。

2)上述Matlab程序有2个测试自变量和4个测试结果变量，具体含义如表1中说明。

表1　Matlab程序中的各个变量

4计算结果对比与讨论

对于结果变量不妨作如下3点规定。

1)若Qsum0不能在step→0时，小于且收敛到某一值，则标准中的公式有误；

2)若Qsum或者D不能在step→0时，小于且收敛到某一值，则修正公式有误；

3)若n→∞或者说step→0时，tsum趋近于1，则本文提出的算法达到精度要求，符合正态分布之和趋近1的规律。

对区间n从小到大取了7个值，用上述Matlab程序进行计算，得到的试验结果如表2所示。

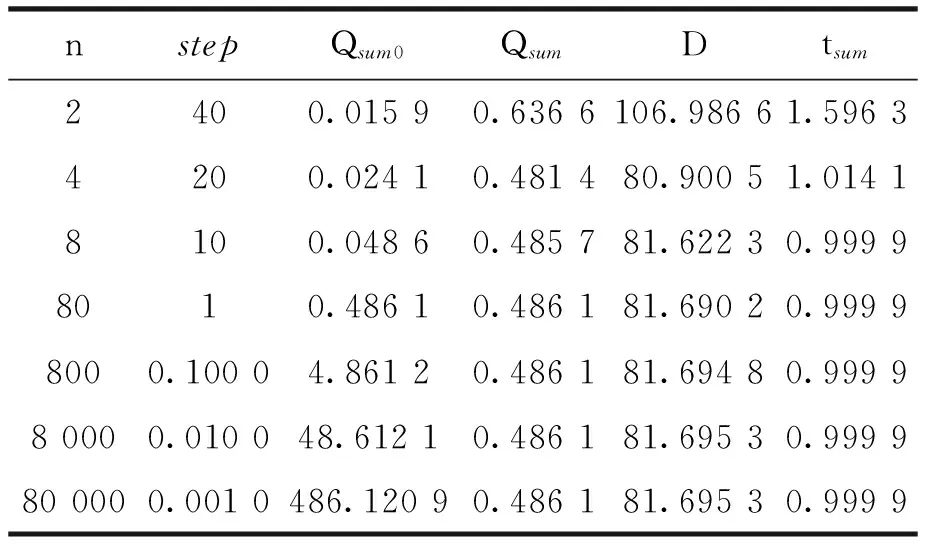
表2　Matlab程序对不同n的试验结果

对试验结果作如下3点分析与讨论。

1)随着n的增大，现有标准中的公式计算出的Qsum0值并不收敛；对比Qsum值，有收敛的结果；只有在n=80，即step=1时，Qsum0和Qsum才相等。

2)随着n的增大，温度区间step逐渐精细，得到tsum越来越趋近于1，并且小于1。这符合正态分布概率密度积分的规律，表明可以用本文的Qsum算法计算绝缘子预期电荷量Q50的近似值。

3)计算表明，在老化试验电压为100kV，试验温度为130℃时，老化试验的时长应为81天。

5结束语

经过对绝缘子预期电荷定义与计算的分析，发现现有标准对绝缘子预期电荷的计算公式有值得探讨之处，主要是因为标准中公式在离散求和时，没有考虑到离散区间和其可变性。经过对现有计算公式的修正与Matlab数值计算的实现，得到了一组较为精确的预期电荷量和老化试验的时间。

参 考 文 献

[1]GB/T19443—2004标称电压高于1000V的架空线路用绝缘子[S]. 北京：中国标准出版社，2004.

[2]丘志贤. 绝缘子产品的可靠性[J]. 电瓷避雷器，1995(1):26-32.

[3]朱海涛，万荣兴，方勇，等．直流盘形悬式绝缘子离子迁移机理研究[J] ．电网与水力发电进展，2008，24(3)：30-36.

[4]李岩冰. 高压直流绝缘子表面电场分布的研究[D].辽宁：沈阳工业大学，2013.

[5]陈豪. 500kV直流支柱式瓷绝缘子离子迁移的研究[D].北京：华北电力大学，2003：7-9.

[6]刘杰. 基于微观性能分析的复合绝缘子老化特性研究[D].保定：华北电力大学，2013.

[7]危鹏，胡文岐，刘志强，等. 直流盘形悬式绝缘子离子迁移测试系统的研究[J]. 电瓷避雷器，2007(2):12-15.

[8]张纪伟. 环氧树脂纳米复合介质表面电荷动态特性与电痕破坏研究[D].天津：天津大学，2012.

[9]刘洋. 交流复合绝缘子老化性能试验研究[D].武汉：武汉大学，2009.

Calculation of Insulator Expected Charge Q50

SUN Changhai1，WANG Ming1，WU Yan1，MA Haifeng2，GE Hengxu3，ZHAO Weicheng1，CHEN Baitong1

(1.SchoolofElectricEngineering，DalianUniversityofTechnology，Dalian116023，China; 2.StateGridHegangElectricPowerSupplyCompany，Hegang154101，China; 3.StateGridDalianElectricPowerSupplyCompany，Dalian116001，China)

AbstractInsulator，is an essential instrument in electrical power system.When insulator works under DC environment，Its inside will exist ions migration，which causes its insulant performance degradation. In this consideration，a series of tests are required for each insulator product，such as aging test，and before all these tests，expected charge is required to get calculated. The definition and calculation of insulator expected charge have been analyzed in this paper，as the equations on available standard are insufficient. A modified equation and its numeric calculation have been demonstrated and realized in Matlab，and then，proceeded and proved，getting a set of much precise results. This paper provides essential references for further insulator aging mechanism and test.

Key wordsinsulator; expected charge; aging test; numeric calculation

收稿日期:2015-05-25；修改日期: 2015-12-24

作者简介：孙长海(1982-)，男，硕士，主要从事电力系统方面的工作。

中图分类号TM76

文献标志码A

doi:10.3969/j.issn.1672-4550.2016.02.017