一种改进的基于混沌的数字图像隐藏算法研究与实践*

蔡正保，姜　红

(安徽国防科技职业学院 信息工程系，安徽 六安 237011)



一种改进的基于混沌的数字图像隐藏算法研究与实践*

蔡正保，姜红

(安徽国防科技职业学院 信息工程系，安徽 六安 237011)

摘要:数字图像隐藏是近年非常热门的研究领域，混沌技术也经常运用到数字图像隐藏过程中.论文提出一种结合混沌和替换算法的改进的数字图像隐藏算法，改进的技术可以使得图像0、1低位随机均匀分布，去除统计的不对称性，图像的直方图异常得到较好的改善.

关键词:数字图像；混沌；替换；隐藏；实践

在信息隐藏技术中，若简简单单地使用信息隐藏算法来隐藏秘密信息，攻击者使用现有的各种信息提取算法对截获的秘密信息进行攻击，就有可能提取出秘密信息.因此，采用普通的、简单的信息隐藏算法去对秘密信息进行隐藏不是一个好的选择[1].为了提高图像隐藏的安全性和效率，至今已经有了很多图像隐藏方案.其中，基于混沌的图像隐藏算法机密性较好.混沌对初始值和系统参数比较敏感，混沌具有白噪声的统计特性，以及混沌序列的遍历特性等.混沌序列有比较优良的密码学特性[2].

1混沌系统

在图像隐藏技术中，可以采用混沌系统进行协助以提高图像隐藏质量.这里需要的混沌序列可以使用确定性方程来产生.当确定性方程确定了初值和参数值时，产生的混沌序列可以重现混沌现象[3].混沌序列对确定性方程的初值非常敏感，并且产生也比较方便，能够复制，密钥易于管理[4]；产生混沌序列的长度可以根据实际应用进行调整，并且呈现非周期性，无密钥情况下难以解密，安全性高.

1.1Logistic映射方程

本文使用Logistic映射方程为：

xn+1=μxn(1-xn),x∈(0,1)

(1)

在式(1)中，μ为分支参数，当μ值发生变化，序列也会出现混沌性或周期性的状况.在μ∈(0,3.57]的情况下，xk为周期函数，周期是2m.要想得到混沌序列，可使Logistic映射处于混沌状态，此时，μ∈(3.57,4]，可以根据需要生成不收敛、非周期的混沌序列.

1.2混沌序列

在加密算法实现的过程中，有时要把混沌映射的轨迹转换成一些不同类型的混沌伪随机序列.

以下是一些常见的混沌序列形式：

(1)实数值数列，直接由混沌映射的轨迹点形成.数列为：{Xk,k=0,1,2…}.

(2)位序列，在实数值序列的基础上产生，在有限精度2-L情况下，能够生成二进制数L|bit，形式为：|xk|=b1(xk)b2(xk)……bi(xk)，|xk|的第i位为bi(xk).位序列为：{bi(xk),i=1,2…;k=0,1,2…}.

(3)二值序列，其阈值T可以定义为：

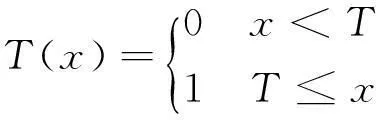
(2)

二值混沌序列可以表示成：{T(xk),k=0,1,2…}.

通过阈值T，混沌序列xk量化成的二值序列W为：

(3)

1.3生成的混沌序列

对常用混沌算法进行改进，结合Logistic映射方程，生成两个Logistic，其长度和秘密信息长度一样.对其中的一个Logistic序列进行处理，求出其均值，也就是对其二值化处理，大于平均值的记为1，小于均值就记为0，二值化处理后的序列记为Logistic1.将秘密信息与Logistic1进行异或运算可得置乱的图像，这样可随机、均匀地分布秘密信息的0、1值，能够避免出现内容相关性[5].

使用Logistic映射方程生成的另外一个序列记为Logistic2，能够用来随机的确定可以嵌入载体图像信息的最低有效位的详细位置信息.根据需要，可对Logistic2进行四值化处理，得到四个不同的序列，利用这四个序列的值可标志秘密图像信息的嵌入位置，即原始载体图像信息的1、2、3、4位面.由于混沌序列的随机性、不相关性，图像隐藏过程中得到的含密图像的统计特性无明显变化.秘密图像的嵌入可采用的方法较多，如替换法、对比法、奇偶法等.为了减小失真，在嵌入时尽量将秘密图像信息嵌入到载体图像的最低位面[6].

2基于混沌的图像隐藏算法

2.1秘密图像嵌入

这里运用Logistic混沌序列改进的最低有效位替换算法对秘密图像进行嵌入.采用前文所述的混沌技术进行处理，得到两个混沌序列，记为Logistic1、Logistic2，再对这两个序列进行二值化处理后嵌入至载体图像的1、2位面.详细嵌入步骤为：

(1)秘密图像置乱.将需要隐藏的二值秘密图像表示为E={e(i,j)|1≤i≤m,1≤j≤n}，采用密钥k1=(x01,μ1)( x01为初值，μ1作为分支参数)辅助生成长度为m×n的混沌序列Logistic1，将其进行二值化处理后再映射成二维矩阵L1={L1(i,j)|1≤i≤m,1≤j≤n,L1(i,j)∈{0,1}}.将E和L1异或位运算得秘密图像EP，EP={ep(i,j)|ep(i,j)=e(i,j)⊕L1(i,j)}.把EP按照行或者列扫描可得一维向量，该一维向量即为要嵌入的序列X=(x(k)|1≤k≤m×n,x(k)∈{0，1}).

(2) 秘密图像嵌入.将选取的载体图像记为C={c(s,t)|1≤s≤M,1≤t≤N}，其第k位面记作Bk={bk(s,t)|1≤s≤p,1≤t≤q,bk(s,t)∈{0,1}}，k∈{1,2,3,4,5,6,7,8}；使用的密钥为k2=(x02,μ2)(x02为初值，μ2为分支参数)；将载体图像运用混沌技术进行处理，生成混沌序列Logistic2，长度为m×n，二值化后可得混沌序列L2={L2(t)|1≤t≤m×n,L2(t)∈{0,1}}.

X的嵌入规则为：当L2(i)=0(k3≤i≤k3+m×n-1，k3为密钥，代表嵌入秘密图像的起始位置，1≤k3≤p×q)时，使用x(i)替换第一位面的值，x(i)=b1(i)；当L2(i)=1时，则使用x(i)替换第2位面的值，x(i)=b2(i).

2.2秘密图像提取

图像提取的过程为嵌入过程的逆过程，详细图像提取步骤为：

(1) 运用密钥k2(x02,μ2)生成长度为m×n的混沌序列，再经过二值处理可得混沌序列L2={L2(t)|1≤t≤m×n,L2(t)∈{0,1}}.

(2) 根据式(4)提取出被嵌入的序列X',再将X'映射成m×n的二维矩阵EP'.

X'={x'(i)|x'(i)=

(4)

(3) 运用密钥k1=(x01,μ1)辅助生成长度为m×n的混沌序列，经过二值化处理并映射成m×n的二维矩阵L1.L1={L1(i,j)|1≤i≤m,1≤j≤n,L1(i,j)∈{0,1}}.再将L1和EP'进行异或位运算，即可提取出秘密图像E'={e'(i,j)|e'(i,j)=ep'(i,j)⊕L1(i,j)}.

3数据仿真和讨论

3.1图像隐藏效果

载体图像选用256×256的灰度lena图，为了对比改进算法的图像隐藏效果，现分别选取256×256、128×128的两个二值图像作为秘密图像.使用改进算法对秘密图像进行隐藏，经过实践应用得图1和图2.其中，图1中原始载体图像(a)和含密图像(c)，通过人体视觉对比无明显区别，原始秘密图像(b)和提取出的秘密图像(d) 通过人体视觉对比也无明显区别.对比图2中图像，结果也是如此.

图1　秘密图像1测试图

图2　秘密图像2测试图

通过实践，秘密图像的隐藏性能指标如表1所示，PSNR为含密图像与载体图像的峰值信噪比.当PSNR值在38db以上时，肉眼便不能感知图像质量的变化[7]，实验数据验证了这里算法的含密图像的视觉隐蔽性比较好，所以，本文改进的图像隐藏算法隐藏效果较好.

表1　图像隐藏分析表

3.2算法安全性分析

采用图像的直方图进行分析测试，对比简单替换算法和改进算法的相关图像的直方图.图3为隐藏秘密图像1的两种算法含密图像直方图，图4为隐藏秘密图像2的两种算法含密图像直方图.对比图3(b)与图3(c),图4(b)与图4(c)，采用简单替换算法会导致含密图像直方图和载体图像直方图出现较为明显的异常[8]；对比图3(b)与图3(d),图4(b)与图4(d)会看到改进算法生成的含密图像直方图和载体图像直方图无明显区别.改进的算法主要使用了混沌序列对秘密图像进行置乱，并随机地决定位置来嵌入秘密图像信息，有效地改善了简单替换算法所引起的图像统计不对称性.

4结语

改进的基于混沌的数字图像隐藏算法计算量小

图3　隐藏秘密图像1的两种算法含密图像直方图

图4　隐藏秘密图像2的两种算法含密图像直方图

的同时图像隐藏效果好，含密图像无明显失真，秘密图像隐藏量比较大；图像信息隐藏技术很多，改进的技术可以使得图像0、1低位随机均匀分布，去除统计的不对称性，并且载有秘密信息的图像和原始图像的直方图异常得到较好的改善，可以更好地实现盲提取；算法符合图像隐藏信息量大、透明性好、安全性高的要求.

参考文献：

[1]李良,李建军.基于数字图像网络传输的混沌加密算法研究[J].无线电工程,2015,10(3):56-57.

[2]卢斌.图像信息隐藏方案的研究与实现[D].西安:西北大学,2011:11-13.

[3]N.K.Pareek,Vinod Patidar,K.K.Sud.Image encryption using chaotic logistic map[J].Image and Vision Computing,2014,24(2):926-934.

[4]郑汉忠.基于混沌序列的数字水印及多路图像加密的研究与实现[D].广州:广东工业大学,2015:23-26.

[5]王唯,刘粉林.基于信息隐藏的混沌JPEG图像加密算法[J].信息工程大学学报,2014,6(2):33-36.

[6]向滔.基于混沌的数字图像加密算法的分析与设计[D].重庆:重庆大学,2014:49-51.

[7]王也隽.信息隐藏技术及其军事应用[M].北京：国防工业出版社,2011:73-74.

[8]Chan C K,Cheng L M.Hiding data in images by simple LSB substitution[J]. Pattern recognition, 2012,37(3):469-474.

(责任编辑:王前)

Research and practice of an improved digital image hiding algorithm based on Chaos

CAI Zheng-bao

(DepartmentofInformationandEngineering,AnhuiofDefenseTechnology,Huangshan,Anhui237011,China)

Abstract:Digital image hiding is a hot research field in recent years, and it is often applied to digital image hiding. This paper proposes an improved digital image hiding algorithm based on chaos and replacement algorithm. The improved technology can make the image 0, 1 low random uniform distribution, remove the asymmetry of statistical image, the histogram of the image is improved.

Key words:Digital image; chaos; replacement; hiding; practice

DOI:10.13877/j.cnki.cn22-1284.2016.06.020

*收稿日期：2016-01-03

基金项目：安徽省自然科学研究重点项目“企业网环境下基于空间域的大容量图像隐蔽传输系统研究”(KJ2016A116)

作者简介：蔡正保，男，安徽六安人，讲师.

中图分类号：TP309

文献标志码：A

文章编号：1008-7974(2016)03-0063-03